基于传递矩阵法的齿轮齿条钻机纵向振动分析

董 峰

（大庆油田有限责任公司第二采油厂，黑龙江大庆163414）①

基于传递矩阵法的齿轮齿条钻机纵向振动分析

董 峰

（大庆油田有限责任公司第二采油厂，黑龙江大庆163414）①

将齿轮齿条钻机简化为线性链式连续多体系统，基于传递矩阵法建立了齿轮齿条钻机各个结构纵向振动的传递矩阵，运用矩阵乘法建立了钻机纵向振动的传递矩阵。分段计算了小车在井架不同高度和1～3 km井深时纵向振动的1阶共振频率，并将模型的计算结果与软件的仿真结果进行了对比分析。研究结果表明：齿轮齿条钻机的系统振动频率主要取决于钻柱长度；井架的高度及升降小车在井架上的运动对钻机系统频率的影响很小，不会改变钻机系统的稳定性。研究结果对齿轮齿条钻机作业有一定指导作用。

齿轮齿条钻机；纵向；振动；传递矩阵；分析

齿轮齿条钻机是新概念石油钻井设备，它将齿条安装在井架上，将齿轮安装在顶驱上，利用齿轮与齿条的啮合带动顶驱上下运动。因此，齿轮齿条钻机既能提供上提力又能产生下压力，能够有效钻进更浅的地层，同时能钻取更多的生产层，更适合定向井、丛式井和水平井钻井及开窗侧钻等钻井工艺［1］。国外齿轮齿条钻机研究早于国内，美国奥格公司、挪威的TTS Sense公司、美国Horizontal Well Drill-ers（HWD）公司和德国的Max Streicher公司是较早从事该项装备研究的公司。经过多年的研究和应用试验，该项技术在国外发展很快，逐渐趋于成熟［2-4］。国内一些专家和学者们也开始该项技术的研究，并取得了一定的研究成果［5-7］。

虽然国内外对钻机的多功能性一直很关注，但对其多体动力学问题的研究较少，钻机系统动力学的研究未见报道。本文以齿轮齿条钻机系统为研究对象，基于传递矩阵法分析了齿轮齿条钻机系统纵向振动的特性，为该钻机的钻井作业提供一定的理论指导。

1 齿轮齿条钻机模型简化

齿轮齿条钻机的结构如图1所示。井架通过钻机底座固定在地面上，齿条固定在井架上，齿轮和顶驱都安装在升降小车上，通过升降小车上的齿轮与安装在井架上的齿条啮合，带动顶驱上下运动，进而实现钻井作业。

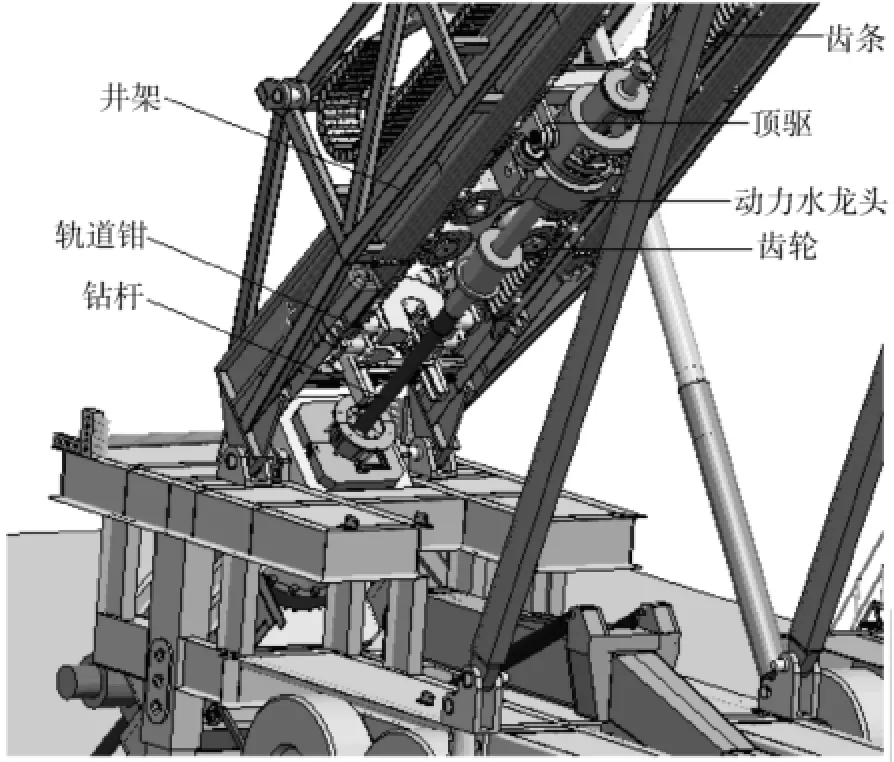
图1 齿轮齿条钻机系统结构

钻井过程中，由于钻头牙齿间断地与地层接触或岩石的间歇破碎，导致钻头振动，最终引起钻柱沿其轴向的纵向振动。钻机发生纵向共振时，钻柱内部的交变应力和振幅相当大，易导致钻柱断裂或粘扣。在分析钻机钻井过程的整体纵向振动时，可将钻柱等效为管柱单元，小车系统等效为刚体系统，井架等效为梁单元。不考虑间隙和阻尼作用，忽略减速器里的齿轮传动引起振动的改变，基于上述分析和齿轮齿条钻机特有的结构形式，将齿轮齿条钻机的纵向振动简化为如图2所示的纵向振动系统。

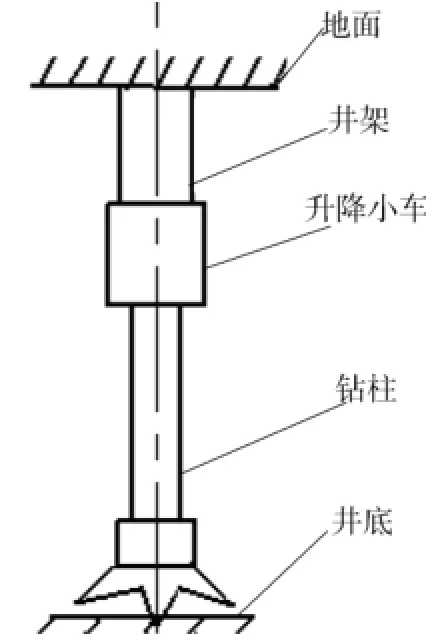
图2 齿轮齿条钻机纵向振动系统简化模型

2 传递矩阵模型的建立

对钻机纵向振动进行分析时，振动的横截面可认为保持平面且和原截面保持平行，在这些截面上的点只作沿轴向方向的运动，忽略纵向振动产生的横向变形。

2.1 钻柱模型的传递矩阵

钻柱的纵向振动研究可以近似看作其在某个平面上作纵向振动，在其位移方向上施加分布载荷；对钻柱底端受到岩石的作用以及钻井过程中所受的其他作用，看作与时间和位移有关的分布力计算。设钻柱总长度为L，钻柱的轴线方向取为x轴。记钻柱在坐标x处横截面积为A（x），弹性模量为E（x），质量密度为ρ（x）。u（x，t）表示坐标为x的截面在时刻t的纵向位移。取微元段d x进行研究，如图3所示，则钻柱纵向振动方程为

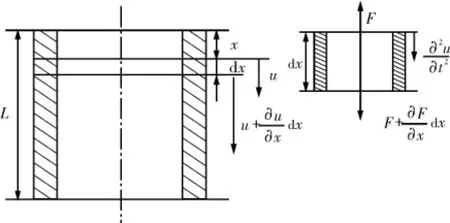
图3 钻柱纵向振动单元分析

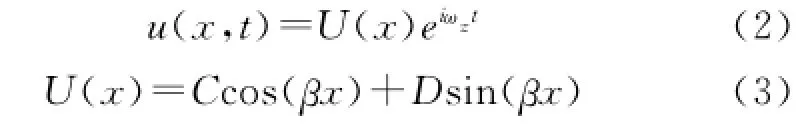
由通解求出状态矢量中其他状态矢量，写成矩阵形式为

2.2 升降小车的传递矩阵

分析齿轮齿条钻机的纵向振动，将整个小车等效为刚体，则刚体纵向振动的传递矩阵为式中：mc为振动刚体的质量；ωc为小车的共振频率。

2.3 井架模型传递矩阵

将齿轮齿条钻机的井架看作等截面长为l的梁，取长为d x的微元段进行受力分析：m为质量线密度；ωj为井架的固有振动频率；E′A′为抗拉刚度；x（x，t）为距输入端x处横截面的纵向位移，如图4所示。

梁的纵向振动动力学方程可以表示为

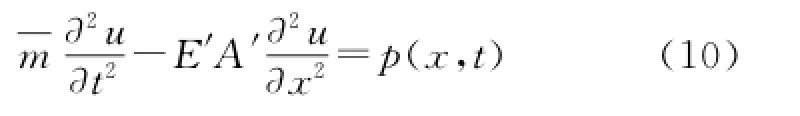
假设井架单元内无集中质量和弹簧-质量单元，不考虑阻尼作用，则该微元段的自由振动运动微分方程为

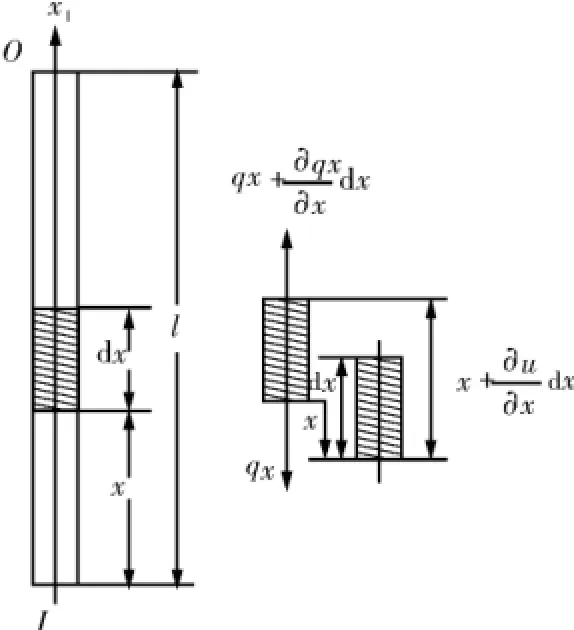
图4 井架及其微元体受力分析

2.4 齿轮齿条钻机整体传递矩阵

根据前文对齿轮齿条钻机系统的等效和分析，利用传递矩阵乘法的计算，将系统的传递矩阵Ui（i＝1，2，3）代入，则有

3 模型解算与分析

钻柱传递矩阵U1、U2、U3均为2×2矩阵，故总体系统传递矩阵U也是2×2矩阵，设

在计算整体共振频率时，将钻柱井架和小车看作1个系统，则该系统的共振频率由系统本身决定。因此，当考虑整体系统的共振频率时，钻柱、小车、井架的固有振动频率选择为系统的固有振动频率ω，下文计算将前文中的ωz、ωc和ωj一律替换成整个系统共振频率ω。

假设钻柱受力为零时，代入边界条件。系统底端为自由振动，系统顶端为固定，则有底端Z0，1＝［X 0］T0，1，顶端振动边界为Z4，3＝［0 Fjj］T4，3，因此频率函数为a11＝0。可得

由式（22）可得，齿轮齿条钻机整体纵向振动的共振频率与井深、井架特性以及系统的固有频率有关。假设井深及小车在井架上的高度，选用ø114.3 mm（4 1/2英寸）钻杆，忽略钻铤长度，得到系统纵向振动第1阶共振频率，如表1所示。

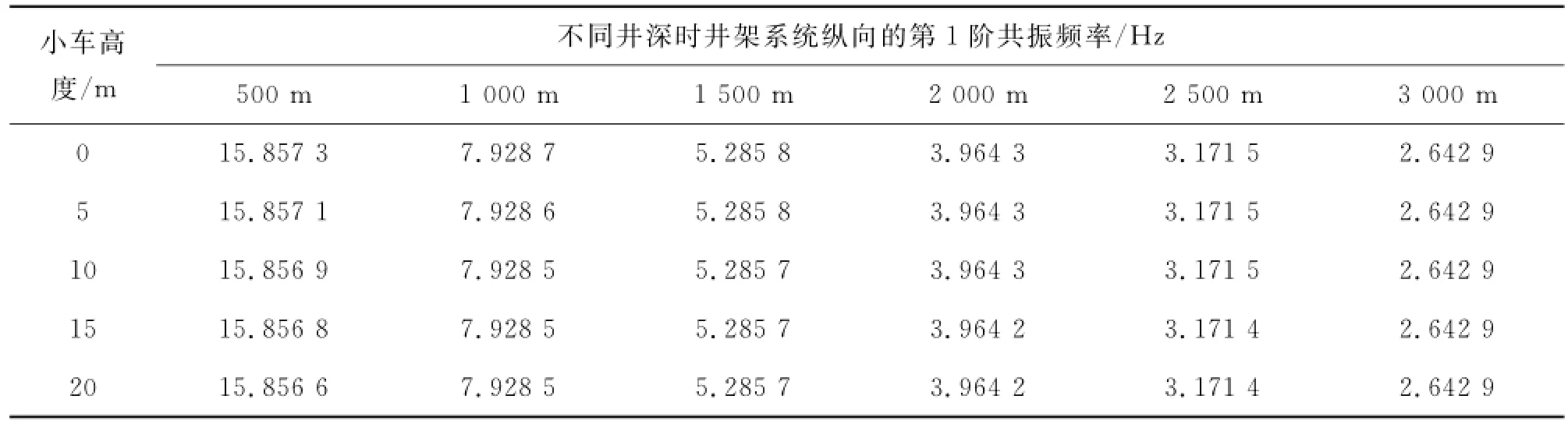
表1 井深及小车在井架上高度与系统共振频率的关系

忽略钻铤长度，设岩石冲击的振动激励为时间的函数。取井深为500 m时，基于动力学仿真软件Adams得到井架（取井架顶端）运动状态和钻杆（取钻杆最底端）的运动状态，如图5～6所示，进而得到钻机振动的1阶共振频率。

图5中：图线1表示钻杆的振动位移；图线2表示变形速度，对应的均为左端纵向坐标值；图线3表示钻杆内部所受力的大小，对应右端纵向坐标值。图6中：图线1表示钻头的位移，对应的纵向坐标值为左端第2列；图线2表示钻头位移速度，对应的纵向坐标为右端值；图线3表示钻头位移加速度，对应的纵向坐标为左端第1列。同理，可以得到不同井深时，齿轮齿条钻机纵向振动的响应图像。

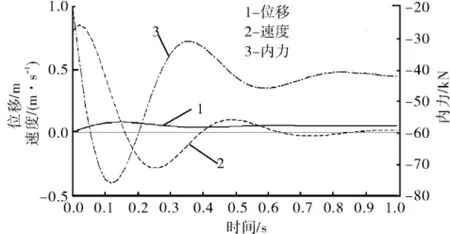
图5 500 m井深井架顶端位移、速度与内力曲线

图6 500 m井深钻杆底端位移、速度和加速度曲线

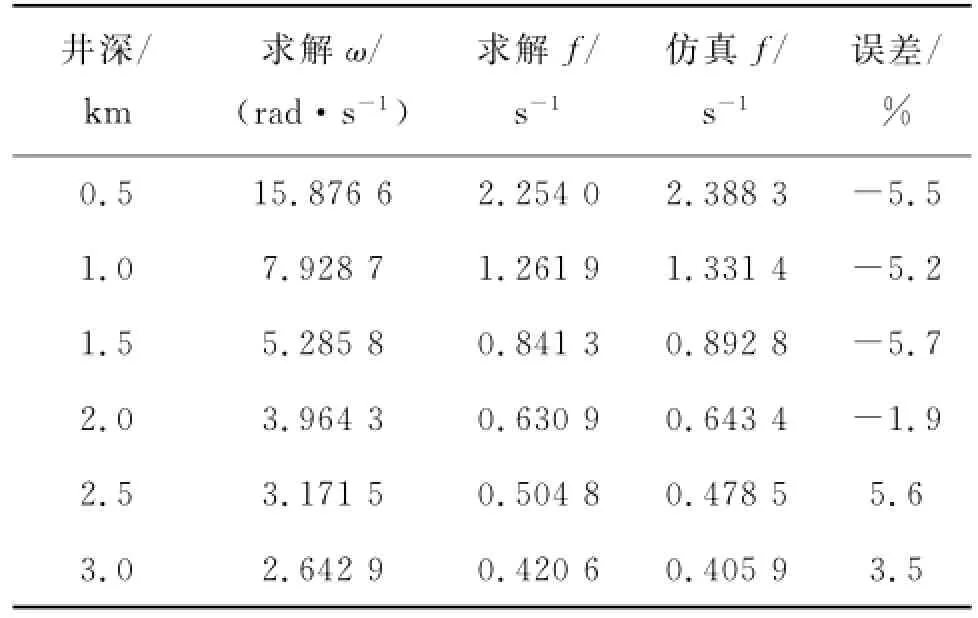
表2 理论求解与仿真结果对比

分析表2中数据，理论计算数值与仿真结果略有误差，但相差不大，主要原因有以下几种：

1） 理论建模将小车等价为刚体，看作集中质量的传递。

2） 理论建模求解时，为计算方便，舍弃了一些次要条件。

3） 仿真时模拟时间和步数的选择也会引起结果的误差。

研究表明：齿轮齿条钻机共振频率与钻柱和井架的固有频率都有关系。钻柱的选择很大程度上决定了系统纵向共振的频率范围，井架的刚度比钻柱刚度大数倍数量级，引起钻机共振频率的减小，但影响微弱。浅井500 m时，使得共振频率降低了0.004 4%，在井深2 500 m时，频率降低了0.003 1%；当井深超过3 000 m时候，数据显示没有影响。因此井架的刚度对钻机系统振动的影响很小，深井钻井时井架不会影响钻机系统的稳定性。

4 结论

1） 基于传递矩阵法建立齿轮齿条钻机纵向振动的数学模型，得到了不同井深钻机整体纵向振动的1阶共振频率。

2） 齿轮齿条钻机的系统振动频率主要取决于钻柱的长度，井架的高度和升降小车在井架上的运动对钻机系统频率的影响很小，不会改变钻机系统的稳定性。

［1］ 王进全，王维旭.国外钻机技术现状及我国的发展策略［J］.石油机械，2011，39（6）：65-69.

［2］ NeilE Borgman，Muskego，WI（US）.BLASTHOLE DRILL WITH ROTARY HEAD CARRIAGE RESILIENTLY HELD ON A MAST：US，6510908 B2［P］.2003-01-28.

［3］ Thorsten nirks.DRILLING DEVICE AND METHOD FOR DRILLING A WELL：US 6857483 B1［P］.2005-02-22.

［4］ William G Riel，Wooster OH.APPARATUS AND METHOD FOR MODIFIED HORIZONTAL DIRECTIONAL DRILLING ASSEMBLY：US 7318491 B2［P］.2006-01-15.

［5］ 王文尔，张军帅，尹永晶，等.2000 m全液压齿轮齿条钻机［J］.石油机械，2011，39（2）：58-63.

［6］ 任福深，王威，刘晔，等.基于AMESim的齿轮齿条钻机动力头起升装置液压系统仿真分析［J］.石油矿场机械，2012，41（5）：14-17.

［7］ 任福深，程晓泽，马若虚，等.齿轮齿条钻机相似样机研制［J］.科学技术与工程，2011，11（29）：7 266-7 268.

Analysis of Longitudinal Vibration of Gear and Rack Based on Transfer Matrix Method

The rack and pinion drilling is simplifyed to linear chain continuous multi-body system，longitudinal vibration transfer matrix of each structure of which is build based on transfer matrix method，and then the transfer matrix of which is build by applying the matrix multiplication.The first resonance frequency of longitudinal vibration is calculated in different height of the derrick and 1 000-3 000 m depth，and results of model calculating and software simulation are analy-zed in comparison.The results show that the vibration frequency of rack and pinion drilling mainly depends on the length of the drill string，the height of the derrick and movement of derrick have little impact on frequency of drilling，and will not change the stability of the drilling system.The results have certain guiding role for operation of rack and pinion drilling.

rack and pinion drilling；longitudinal；vibration；transfer matrix；analysis

TE922

A

10.3969／j.issn.1001-3842.2014.11.005

1001-3482（2014）07-0018-05①

2014-01-09

国家自然科学基金项目（11372071）；中国博士后基金项目（2013 M541139）；黑龙江省科技攻关项目（GZ11A405）

董 峰（1977-），男，黑龙江大庆人，工程师，硕士，主要从事油气生产技术开发工作。