深埋双圆盾构隧道的横向地震响应特性研究

姚超凡,晏启祥,何 川,耿 萍

深埋双圆盾构隧道的横向地震响应特性研究

姚超凡,晏启祥,何 川,耿 萍

(西南交通大学交通隧道工程教育部重点实验室,成都 610031)

阐述反应位移法的基本原理和深埋双圆盾构隧道的地层荷载模式,并基于反应位移法和梁弹簧模型,对双圆盾构隧道仅受静载和静载与水平剪切地震荷载同时作用下结构的变形和内力等动力响应特性进行研究。分析表明:与对称静载作用下相比,在静载与地震荷载同时作用时,结构的变形和内力不再是对称的;弯矩和变形走势基本一致,两洞各自上半圆的迎地层位移侧和下半圆的背地层位移的衬砌基本都有向洞内的位移和内侧受拉的弯矩,两洞各自上半圆的迎地层位移侧和下半圆的背地层位移的衬砌基本都具有相反方向的位移和弯矩,与中柱底部连接处的弯矩集中现象得到消除;衬砌的轴力不再是全部为受压值,而是出现大范围受拉的情况,且拉力值较大,中柱的压力值减小十分明显;与中柱连接处的剪力集中现象消除明显,远离中柱处的管片衬砌剪力绝对值增大明显。

双圆盾构隧道;水平剪切地震;反应位移法;横向动力响应

Key words:double-o-tube shield tunnel;horizontal shear seismic load;response displacement method; transverse dynamic response

1 概述

双圆盾构隧道是由2条单圆单线隧道并行搭接而成[1],其可由双圆盾构机一次推进而完成修筑。双圆盾构技术具地下空间利用效率高、施工费用少等优点[2-3],在有空间限制或制约的地铁线路中有极大的推广价值。1988年,双圆盾构技术在日本铁路京叶线京桥隧道中首次被采用,2003年,我国首次也是唯一一次采用双圆盾构技术建设了上海轨道交通M8线黄兴绿地站至翔殷路站区间隧道,标志着双圆盾构隧道技术开始进入中国。至今,该技术在我国的研究和应用基本处于停滞状态。

目前,国内对双圆盾构隧道为数不多的研究主要集中在静载作用下管片衬砌内力分析和地表沉降方面,如文献[4,5],而对双圆盾构隧道的地震响应特性的研究还很少。虽然文献[6,7]都涉及到双圆盾构隧道的地震响应分析,但未对双圆盾构隧道的横向地震响应特性进行深入的分析和探讨。文献[6]从隧道结构抗震稳定性的角度探讨了双圆盾构隧道的横纵向地震反应,但其并未对横向动力特性进行研究,也未得出一般性的结论。文献[7]虽然对震前震后结构的内力进行了对比,但其研究重点主要集中在有无立交结构的抗震分析。有鉴于此,本文基于反应位移法和梁-弹簧模型,对双圆盾构隧道在静载作用下和静载与地震荷载同时作用下的变形和内力进行对比分析,并对双圆盾构隧道的横向动力特性进行探讨。

2 反应位移法原理

反应位移法中的地震荷载由隧道周边天然地层的剪切力、隧道两侧受到的强制位移和惯性力三部分组成,由于惯性力对隧道结构的影响很小,通常忽略[8],故而盾构隧道的反应位移法分析模型可表示为如图1所示。图1(a)为天然地层的地震响应,图1(b)为作用在双圆盾构隧道衬砌上的地震荷载。

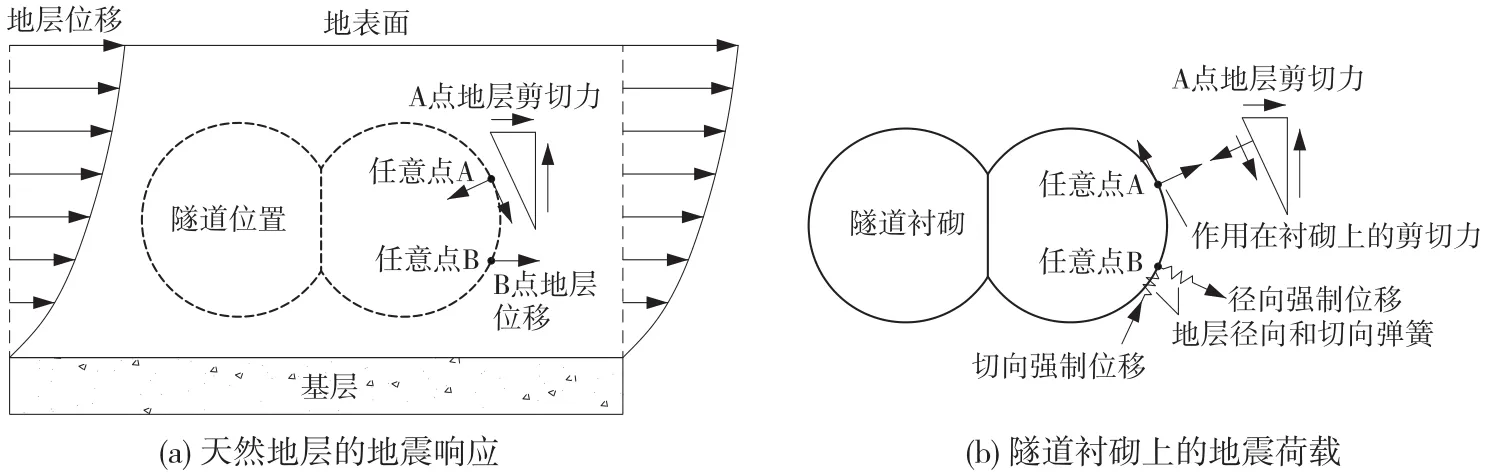
图1 反应位移法分析模型

反应位移法计算流程为[9-10]:计算地震时隧道断面所在天然地层的位移响应,见式(1),然后以强制位移的形式施加到地层弹簧末端节点上;通过式(2)计算剪切应力,再通过式(3)和式(4)将剪切应力沿衬砌的法线和切线方向进行分解,并施加到隧道衬砌上;分别对地震荷载作用和常时静载作用进行结构计算,然后将二者的计算结果进行叠加即可获得隧道抗震设计所需断面内力

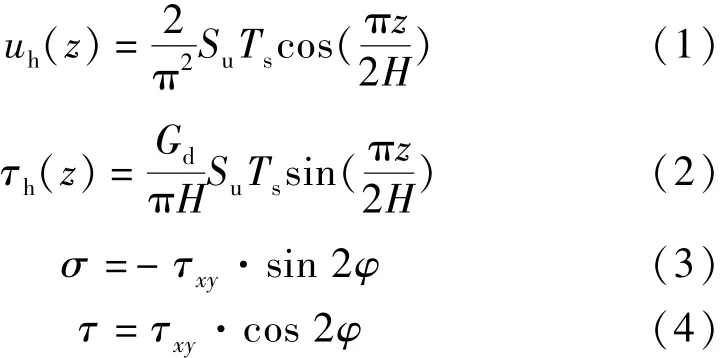
式中,Su为地层基岩面的速度反应谱;Ts为地层的自振周期;Gd为地层动剪切弹性模量;H为地表到基岩的距离;z为原点为地表的向下坐标系变量;φ为从x轴正向逆时针旋转的角度。

3 深埋双圆盾构隧道的地层荷载

目前,国内双圆盾构隧道荷载确定无成熟的经验或公式,本文使用文献[11]中的深埋双圆盾构隧道地层荷载模型。该模型基于单圆盾构隧道的Terzaghi公式提出。考虑到双圆隧道中柱的存在,盾构脱环后中柱旋即开始承受压力,因此若按整个开挖跨度计算垂直压力势必偏大;与此同时,考虑到盾构施工导致的地层损失,隧道计算松动压力的宽度若选择双圆隧道的一半又将偏小。故而,双圆盾构隧道松动压力计算值在半结构宽度与整个开挖宽度对应的松动压力之间选取将更加合适。双圆隧道竖向荷载宜按图2(a)阴影外轮廓线与拱顶之间的土柱荷载,即阴影外轮廓线作为深埋双圆盾构隧道竖向荷载选取。根据图2(a)阴影外轮廓线包围的范围,可将双圆盾构隧道的竖向荷载近似处理成图2(b)的形状,在单圆松动压力的基础上增加中柱顶部一定范围的附加压力,即阴影部分土柱的面积以及中柱与两侧拱肩所夹部分土体的自重,并将增加的两部分地层压力近似简化成三角形分布。

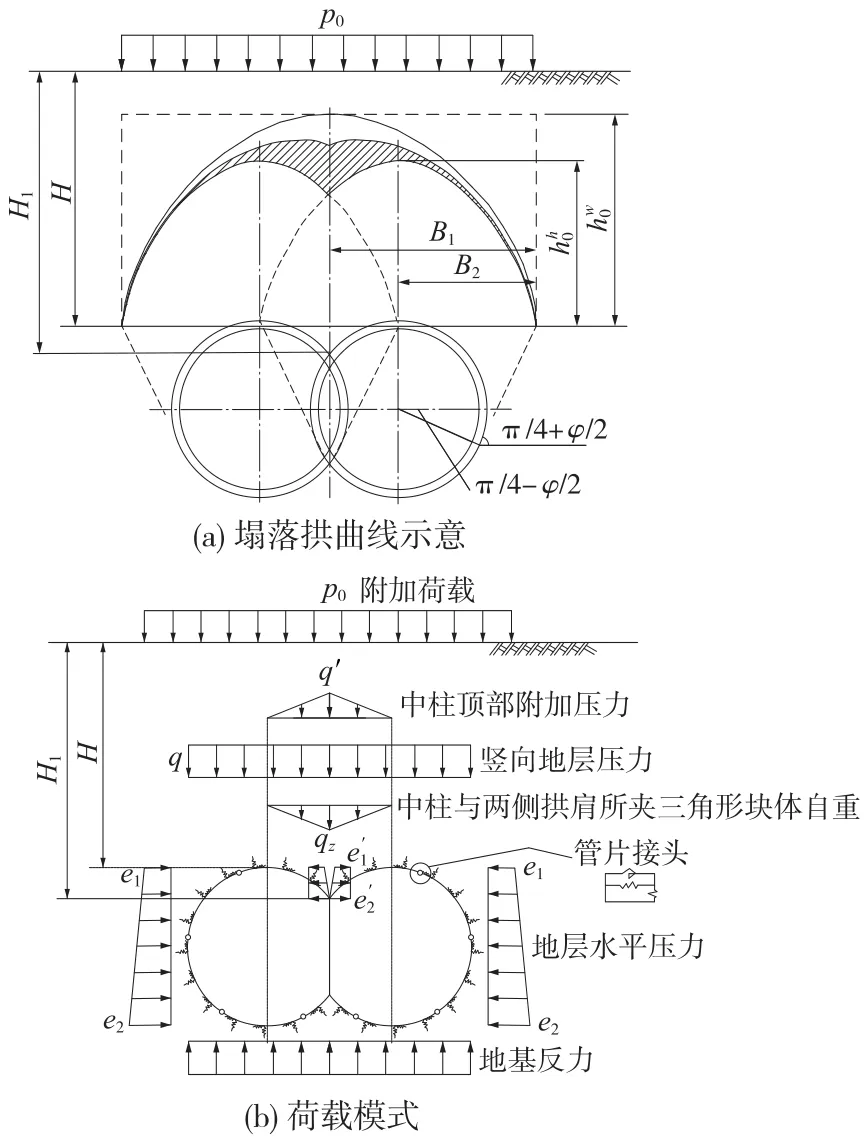
图2 深埋双圆盾构隧道荷载模式

根据图2,双圆盾构隧道顶部垂直压力及其中柱顶部压力为

式中,q为隧道垂直均布压力,kN/m2;q′为隧道中柱顶部附加压力,kN/m2;qz为中柱与两侧拱肩所夹三角形块体自重,kN/m2;γ为地层重度,kN/m3;hw0与hh0可根据Terzaghi公式计算,m;ξ为附加荷载修正系数,一般取0.5～0.7;H1为隧道中柱顶部到地面的距离,m;H为隧道顶部到地面的距离,m。

双圆盾构隧道的侧向压力和基地反力的计算方法与单圆盾构隧道的计算方法相同,不再赘述。

4 双圆盾构隧道的横向地震响应分析

4.1 分析对象

某地铁双圆盾构隧道选取的计算断面处于均质黏性土层当中,遭受水平剪切地震波作用,求其横向地震响应。黏土的天然重度γ=20.0 kN/m3、内摩擦角φ= 18°、黏聚力c=14 kPa,黏土厚36 m,其下为基岩,隧道顶部埋深25 m,大于式(5)中竖向荷载对应的等效土柱高度的1.5倍,可视为深埋。经计算,其动剪切模量Gd=93.8 MPa,基岩面速度反应谱Su=0.093 2 m/s,土层的自振周期Ts=0.917 s,地层弹性抗力系数径向K1=11.5 MN/m3,切向K2=3.85 MN/m3。衬砌由预制钢筋混凝土管片拼装而成,每环管片由8块A型标准块、1块B型(海鸥形管片)、1块C型(小海鸥形管片)、1块D型(中立柱连接B块与C块)共11块管片构成,相邻两组管片之间采用错缝拼装,衬砌的拼装如图3所示。管片宽1 200 mm,厚350 mm,混凝土密度2 500 kg/m3,弹性模量32.5 GPa。

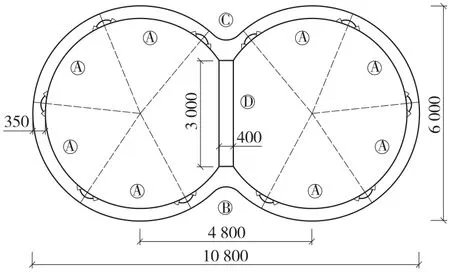
图3 管片拼装(单位:mm)

4.2 分析模型

采用梁-弹簧模型进行分析,如图4所示。用梁单元模拟管片衬砌,杆单元模拟中柱,管片接头采用拉压弹簧、剪切弹簧和抗弯弹簧进行模拟,地层径向力和切向力的传递分别采用仅受压的杆单元(受拉时杆单元上的力为零)和弹簧单元模拟。

图4 梁弹簧模型

管片接头的拉压弹簧、剪切弹簧的刚度分别取3.71 GN/m和1.44 GN/m,管片衬砌内部受拉时抗弯刚度取179.76(MN·m)/rad,管片衬砌外部受拉时抗弯刚度取40.37(MN·m)/rad[12]。施加在地层弹簧上的强制位移和施加在管片衬砌上的剪切力可以根据反应位移法的基本原理进行计算。

4.3 双圆盾构隧道的横向地震特性

对双圆盾构隧道计算断面进行静力分析(以下简称工况一),然后采用反应位移法计算静载和地震荷载同时作用(以下简称工况二)时结构的变形和内力,再将二者的计算结果进行对比分析。计算结果为基于幅宽为1.2 m时管片衬砌与中柱的变形和内力值。

计算获得的两种工况下的变形情况如图5所示,变形值按两种工况各自的变形区段变形极值进行标注。常时静载作用下,双圆盾构隧道的变形沿中柱对称分布,两洞各自的拱顶拱底向内侧变形,最大值出现在拱底处,其值为1.16 mm,两侧拱腰向外侧变形,最大值为1.45 mm。在静载和地震荷载同时作用时,变形值为总位移中去除强制位移后的值,两洞各自的左上方和右下方皆向洞内变形,其最大值出现在左洞右下方处,其值为3.64 mm,两洞各自的右上方和左下方皆向洞外变形,其最大值出现在右洞左下方处,其值为3.29 mm。

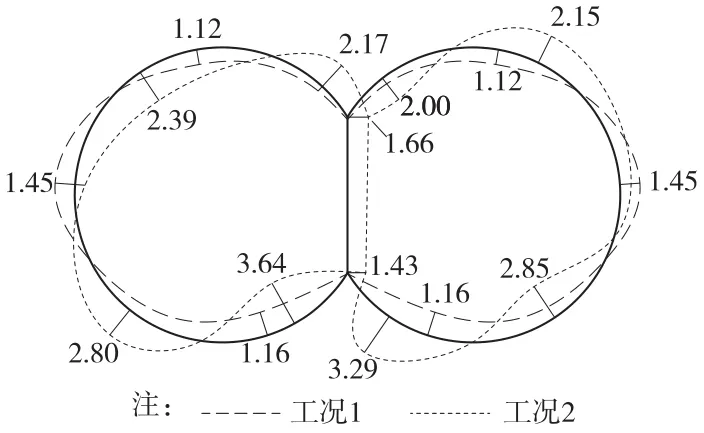
图5 双圆盾构隧道变形示意(单位:mm)

计算获得的两种工况下的弯矩图如图6所示,弯矩以内侧受拉为正,弯矩值按工况二中各弯矩正负区段的极值进行标注。常时静载作用下,双圆盾构隧道的弯矩呈对称分布,两洞各自的拱顶拱底的弯矩都为正值,两侧拱腰的弯矩皆为负值且弯矩值较小,管片衬砌与中柱底部的连接处弯矩集中现象明显,最大负弯矩也出现在该处,其值为98.5 kN·m。在静载和地震荷载同时作用下,双圆盾构隧道的弯矩走势基本呈反对称分布,两洞各自的右上侧和左下侧的弯矩均为负值,最大负弯矩出现在左洞左下侧,其值为-61.5 kN· m,两洞左上侧和右下侧的弯矩为正值,最大正弯矩出现在左洞左上侧,其值为55.7 kN·m;管片衬砌与中柱底部连接处的弯矩非常小,其值仅为-6.5 kN·m。

图6 弯矩图(单位:kN·m)

计算获得的两种工况下的轴力值见图7,轴力以受拉为正,除管片衬砌与中柱顶部和底部连接处外,图7中轴力值的标注间隔为45°。常时静载作用下,结构的轴力呈对称分布,管片衬砌和中柱均受压,管片衬砌的最大受压值出现在管片衬砌与中柱底部的连接处,其值为-939 kN,中柱的最大受压值出现在中柱底部,其值为-1 385 kN。在静载和地震荷载同时作用时,两洞各自的圆心以左的衬砌基本处于受拉状态,且拉力值较大,最大值出现在左洞左下方,其值为490 kN;两洞圆心以右的衬砌基本处于受压状态,最大压力值出现在右洞右下方,其值为621 kN;中柱受到的压力值很小,中柱中点压力值仅为-75 kN。

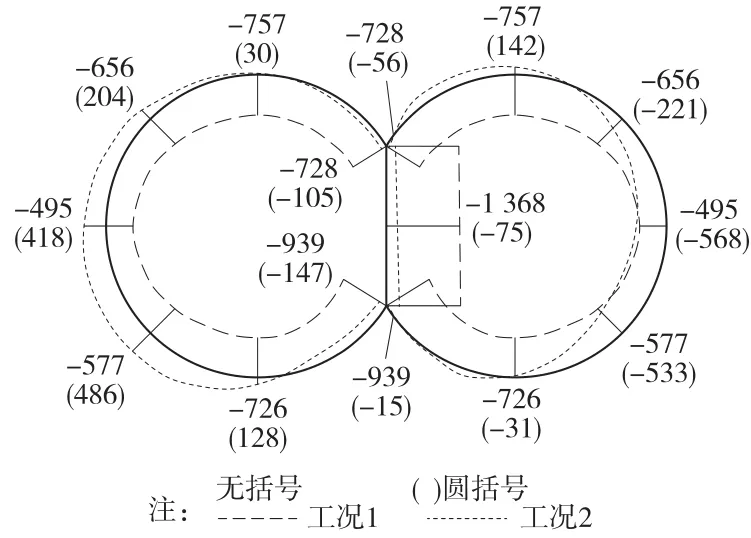
图7 轴力图(单位:kN)

计算获得的两种工况下的剪力值见图8,图8剪力值按工况二中各剪力正负区段的极值进行标注。常时静载作用下,结构的剪力分布走势基本呈反对称,在两洞与中柱底部连接处剪力集中现象明显,正负剪力极值也出现在该处,分别为92.7 kN和-192.7 kN,远离中柱的管片衬砌的剪力值较小。在静载和地震荷载同时作用时,结构的剪力走势基本呈对称分布,最大剪力值出现在管片衬砌与中柱顶部的连接处,其值为69.0 kN,最小剪力值出现在左洞左拱腰处,其值为-47.0 kN,两洞与中柱底部连接处剪力值减小明显。

图8 剪力图(单位:kN)

5 结语

阐述了反应位移法的基本原理和深埋双圆盾构隧道的地层荷载模型,基于反应位移法和梁-弹簧模型,对比了静载作用和静载与地震荷载同时作用时双圆盾构结构的变形和内力分布规律,对双圆盾构隧道的动力特性进行了分析。研究表明,与常时静载作用相比,静载和地震荷载同时作用时双圆盾构隧道表现出如下特性。

(1)变形情况:变形不再是对称的,两洞各自上半圆的迎地层位移侧和下半圆的背地层位移侧基本向洞内变形,两洞各自上半圆的背地层位移侧和下半圆的迎地层位移侧基本向洞外变形,最大变形值增大明显。

(2)弯矩分布:两洞对应位置弯矩值的正负情况基本相反,其分布走势与变形走势相似,两洞各自上半圆的迎地层位移侧和下半圆的背地层位移侧弯矩为正值,两洞各自上半圆的背地层位移侧和下半圆的迎地层位移侧弯矩为负值;海鸥型管片与中柱底部连接处弯矩集中现象明显得到消除,除该部分外的管片衬砌的弯矩绝对值增大明显。

(3)轴力分布:管片衬砌不再是全部处于受压的状态,两洞各自圆心以左的管片衬砌出现大范围受拉状态,且拉力值较大,尤以左洞更为明显;受压部分衬砌的极值略有减小;中柱上的受压值减小特别剧烈。

(4)剪力分布:剪力值的走势基本呈对称分布,远离中柱处的管片衬砌剪力值的绝对值增大明显,而与中柱底部连接处附近的管片衬砌剪力值减小明显。

[1] 王峥峥.浅析双圆盾构区间隧道管片设计[C]∥中国交通土建工程学术论文集,2006:31-36.

[2] 孙统立,张庆贺,韦良文,等.双圆盾构掘进施工扰动土体附加应力分析[J].岩土力学,2008,29(8):2246-2251.

[3] 袁金荣,周裕倩,刘学增,等.双圆盾构隧道衬砌结构设计及参数研究[J].岩土工程学报,2005,27(6):638-641.

[4] 胡欣雨.双圆盾构隧道衬砌结构内力计算方法研究[D].上海:同济大学,2007.

[5] 魏纲,陈伟军,魏新江.双圆盾构隧道施工引起的地面沉降预测[J].岩土力学,2011,32(4):991-996.

[6] 吴晓峰,周健,董鹏.软土地层中双圆盾构法隧道的抗震分析[J].工程抗震,2004(4):27-31.

[7] 陈宇,肖龙鸽.双圆盾构穿越下立交结构的抗震特性研究[C]∥第二届全国地下、水下工程技术交流会论文集,2011:268-273.

[8] 晏启祥,刘记,何川.公路盾构隧道地震响应的反应位移法分析[J].公路交通科技,2011,28(4):96-99.

[9] 耿萍,何川,晏启祥.水下盾构隧道抗震设计分析方法的适应性研究[J].岩石力学与工程学报,2007,26(S2):3625-3630.

[10]耿萍.铁路隧道抗震计算方法研究[D].成都:西南交通大学,2011.

[11]晏启祥,程曦,何川,等.深埋双圆盾构隧道衬砌荷载模式及其接头效应分析[J].铁道标准设计,2010(10):92-95.

[12]刘学山.盾构隧道管片横向接头刚度对内力影响的研究[J].现代隧道技术,2003,40(4):14-19.

Study on Transverse Seismic Response of Deeply-buried Double-O-Tube Shield Tunnel

YAO Chao-fan,YAN Qi-xiang,HE Chuan,GENG Ping
(MOE Key Laboratory of Transportation Tunnel Engineering,Southwest Jiaotong University,Chengdu 610031,China)

The basic principle of response displacement method and the stratum load pattern of deeply-buried double-o-tube shield tunnel were described in this study.And then,based on response displacement method and beam-spring model,the structural deformations,internal forces and other dynamical response characteristics of double-o-tube shield tunnel were studied under the action of only static load,as well as under the combined action of static load and horizontal shear seismic load.The study shows that:(a)Compared with those under the action of symmetrical static loads,the structural deformations and internal forces under the combined action of static load plus seismic load are no longer symmetrical.(b)The bending moment trend is basically the same as the deformation trend.For both the two tubes,at the lining of upper half of the circle in face of the stratum displacement,and at the lining of lower half of the circle not in face of the stratum displacement,there are the deformations towards tube inner and the inner-side-tensioned bending moments;while at the opposite linings,the directions of deformations and bending moments are basically opposite to the above-mentioned.The phenomenon of bending moment concentration is eliminated at the place connecting to the middle pillar bottom.(c)The axial forces of the lining are no longer all pressure forces but a wide range of tensile forces with greater amplitudes;and there is obvious reduction of pressure forces of middle pillar.(d)There is obvious elimination of the phenomenon of shear concentration at the place connecting to the middle pillar,while ______there is obvious increasing of shear absolute values at the segment lining away from the middle pillar.

U452.2+8

A

10.13238/j.issn.1004-2954.2014.04.017

1004-2954(2014)04-0074-04

2013-08-03;

2013-08-13

教育部新世纪人才资助项目(NCET-11-0713);国家自然科学基金资助项目(51178400,U1134208)

姚超凡(1990—),男,硕士研究生,E-mail:chaofan.yao@ gmail.com。