强震作用下连续梁桥多墩联合半主动控制

孙松建，姜 南，李忠献

(天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

强震作用下连续梁桥多墩联合半主动控制

孙松建，姜 南，李忠献

(天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

为了平均分配连续梁桥各墩的损伤，提出了一种多墩联合半主动控制算法．该控制算法在主动最优控制力的基础上，综合考虑连续梁桥各墩的损伤状态，通过调整阻尼器的目标出力，在主梁加速度和各桥墩的墩顶与主梁间相对位移得到控制的同时，使各桥墩的损伤指数平均分配．本文以一设置了磁流变(MR)阻尼器的3跨连续梁桥为研究对象，采用MATLAB进行数值模拟分析，对所提出的半主动控制算法进行了多种工况下的验证．计算结果表明，采用多墩联合半主动控制算法能够较好地控制桥梁的地震反应，同时有效降低破坏最严重的桥墩在强震过程中的损伤指数，达到各桥墩损伤平均分配的效果．

连续梁桥；桥墩损伤；磁流变阻尼器；半主动控制；相对位移

近年来，桥梁结构的被动控制研究已经较为成熟．隔震支座作为当前桥梁结构抗震控制的主要装置，其自身所具有的耗能能力可以延长桥梁的基本周期，有效提高桥梁整体的抗震性能．但是，当遭遇的地震强度较大时，隔震支座会产生过大的变形，这不仅会导致支座自身的破坏，而且还会造成桥梁上部结构之间相对位移增大[1-2]，严重时甚至发生碰撞或落梁．而对桥梁结构采用适当的半主动控制，可以有效降低桥梁的地震响应，因此，各国学者对桥梁结构半主动控制的研究应运而生．半主动控制是介于主动控制和被动控制之间的一种控制方式，半主动控制既具有被动控制的可靠性和经济性，还具有主动控制的强适应性，而且构造简单、所需能源小，不会发生能源的溢出问题．因此，半主动控制受到了越来越广泛的关注，成为结构振动控制研究领域的国际前沿性研究课题之一[3-5]．

影响半主动控制效果的一个重要因素是半主动控制策略的选择．目前，国内外主流的半主动控制策略主要采用的控制算法有简单Bang-Bang控制算法、最优Bang-Bang控制算法和限界Hrovat最优控制算法等[6-8]．这些控制策略都能较好地降低结构在地震激励作用下的地震响应，但大都只是针对控制装置所安装位置处的地震响应进行控制研究，没有考虑到构件本身的损伤及对其他构件损伤的影响．对于长大桥梁结构，一旦有一处发生严重破坏，整座桥梁将无法通行，这将阻碍震后的救灾工作，造成巨大的经济损失．因此，研究多墩连续梁桥的半主动控制，需要考虑到各桥墩地震损伤的平均分配，以防止“一处损，全桥断”情况的发生．笔者对限界最优控制算法进行改进，同时考虑了桥梁结构的最大地震响应和各桥墩地震损伤平均分配的多墩联合半主动控制算法，可以抑制破坏最严重桥墩的损伤指数进一步增加，控制各桥墩的损伤指数平均分配．

1 半主动控制策略

半主动控制策略是考虑控制装置控制力输出特性与系统控制力需求或结构运动之间的关系，将不同参数之间比较、判断、取舍的过程用数学公式加以表达的结果．基于不同的判断取舍条件，可形成不同的半主动控制策略，如开关控制策略、多态控制策略以及限幅控制策略等[9]．其中，在对桥梁半主动控制策略的研究中，基于LQR的限界最优控制策略的控制效果，与主动控制的控制效果较为接近，却只消耗半主动控制所需要的能量，是一种较好的连续型半主动控制策略[10]．限界最优控制策略如式(1)所示．

式中：Fmax为磁流变阻尼器相应于主动最优控制力u(t)时刻可能实现的最大阻尼力；cd为磁流变液的黏滞阻尼系数；fcmax和fcmin分别为磁流变阻尼器的最大和最小库仑阻尼力．该控制策略表明，当最优控制力与磁流变阻尼器所在位置振动方向相反时，调节磁流变阻尼器实现最优控制力．如果最优控制力大于此时阻尼器能实现的最大阻尼力，则施加最大阻尼力Fmax；当最优控制力与磁流变阻尼器所在位置振动方向相同时，施加最小阻尼力．这一控制算法正好反映了磁流变阻尼器只能施加阻止结构运动的力，而不能施加推动结构运动的力．

装有磁流变阻尼器的多墩不对称连续梁桥，在强震激励作用下，各墩墩顶处的控制装置对墩顶与主梁间的相对位移响应具有较好的控制效果．各桥墩通过主梁存在着相互联系和相互作用，其损伤指数几乎不会相等，需要降低损伤最大的桥墩的损伤指数，防止一处破坏、全桥不通的结果．在半主动控制中，阻尼器对桥墩只能产生阻止其运动的力，使得墩顶额外受到一个与其运动方向相反的力，势必会增加桥墩的墩底剪力和弯矩及桥墩的变形，从而增加桥墩的损伤．故可通过降低损伤较大桥墩的阻尼器出力，来降低该墩的损伤加剧的程度．基于以上理论分析，在限界最优半主动控制算法的基础上，考虑各墩的损伤指数平均分配，提出一种多墩联合半主动控制策略．该控制策略表示，损伤指数最大的桥墩的控制算法按式(2)进行计算，其余各墩控制力计算的算法仍采用限界最优半主动控制算法．

式中：FDmax为对损伤最大的桥墩施加的半主动控制力；Dmax和Dmin分别为损伤最大和最小的桥墩的损伤指数．式(2)中：当Dmax=Dmin时，采用原限界最优半主动控制算法来计算所需控制力；当0＜Dmax-Dmin＜0.2时，适当降低损伤指数最大的桥墩的半主动控制力，以便降低该墩的损伤加剧的程度；当Dmax-Dmin≥0.2时，损伤指数最大的桥墩的半主动控制力的输出调到最低，防止该墩最终的破坏程度比其他墩大一个破坏等级．上述半主动控制策略的流程如图1所示．

图1 多墩联合半主动控制策略流程Fig.1 Flow chart of multi-pier joint semi-active control strategy

2 损伤指数计算模型

2.1 地震损伤模型

对于上述半主动控制算法，需要在每一个分析步中先计算出各桥墩的损伤指数．目前，国内外的土木工程学者为了合理地反映弹塑性变形和低周疲劳效应对结构地震损伤的影响，已经提出了许多不同类型的地震损伤模型[11]．其中，在地震工程研究领域应用较多的是Park和Ang基于一大批美国和日本的钢筋混凝土梁柱试验提出的双参数地震损伤模型[12-13]，该损伤模型采用的规格化最大位移和规格化滞回耗能线性组合的损伤评估表达式为

式中：D为构件的损伤指数；cux为在单调加载下的破坏位移；mx与hsE分别为构件在实际地震中的最大变形和累积滞变耗能，是损伤计算模型中的变量；yF为构件的屈服剪力；β为构件的耗能因子．β的表达式为

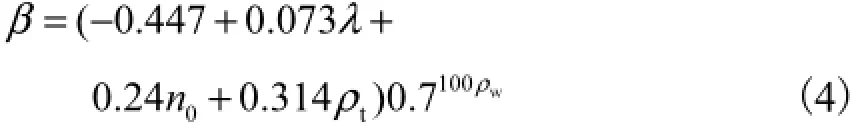
式中：λ为构件的剪跨比，当λ＜1.7时取1.7；n0为轴压比，当n0＜0.2时取0.2；ρw为体积配箍率；ρt为全部纵向受力钢筋配筋率，当ρt＜0.75%时取为0.75%、要在强震过程中的每一个时间步进行测量运算得到．

Park和Ang[13]提出的钢筋混凝土构件地震损伤模型是将构件的弹塑性变形和累积滞变耗能线性组合的地震损伤模型．该损伤模型简单易行，计算速度快，满足结构抗震的半主动控制、需要在0.01,s的瞬间内计算出结构所需控制力的要求．同时，计算模型中的参数比较容易通过测量和计算得到，满足在工程实际中的实用性要求．

2.2 地震震害等级与损伤指数

对于连续梁桥结构体系，计算分析表明，其主梁、桥面板等钢筋混凝土构件在地震作用下很难进入弹塑性状态，该结构体系的损伤主要表现为桥墩和支座的损伤．为了进一步给出结构的震害等级，胡聿贤[14]提出了描述结构地震破坏程度的“震害指数”，并在大量实际建筑结构的震害调查中，给出了各震害等级的震害指数范围，如表1所示．

表1 钢筋混凝土结构震害等级与损伤指数Tab.1 Earthquake damage level and the damage index of reinforced concrete structure

3 算 例

对一座装有磁流变阻尼器的3×30,m的3跨连续梁桥(见图2)进行抗震效果对比分析，并对所提出的控制策略进行分析验证．该桥的两个桥墩墩高分别为6,m和15,m，3跨长均为30,m，桥宽5,m，主梁采用箱梁形式，桥墩为钢筋混凝土矩形截面，桥台和桥墩上的支座采用板式橡胶支座并行摆放．将课题组自行研制的MR-J2a型磁流变阻尼器作为半主动控制装置，并行设置于墩顶与主梁之间．每个墩顶与主梁间共设置8个MR阻尼器，沿桥梁的纵向设置．

图2 桥梁计算模型Fig.2 Bridge computational model

采用纵向输入的天津波和El-Centro波，其加速度峰值调整为200,gal和400,gal．分别对该桥在无控状态(UC)、限界最优半主动控制状态(SAC)以及本文所提出的考虑损伤平均分配的多墩联合半主动控制状态(ADSAC)下进行分析计算．表2中列出了在不同地震激励下，采用上述多种控制策略时桥梁的地震响应和桥墩的损伤指数．图3～图6依次给出了天津波和El-Centro波激励下，p1墩和p2墩墩顶和主梁间的相对位移时程曲线．

从图3和图4中可以看出，在加速度峰值为200,gal的天津波和El-Centro波激励下，两种半主动控制策略下两个桥墩的墩顶与主梁间的相对位移曲线几乎重合．结合表2可以看到，此时两个桥墩的墩顶与主梁间的相对位移峰值相近．而采用多墩联合控制策略下，破坏最严重桥墩的损伤指数和两桥墩的损伤指数之差均略低于采用限界最优半主动控制策略下的值．这说明在中震作用下，两种半主动控制策略的控制效果相近，而多墩联合半主动控制策略下的最大桥墩损伤指数相对略低．

表2 采用不同控制算法时的桥梁地震响应及桥墩损伤指数Tab.2 Bridge seismic response and pier damage index using different control algorithms

图3 在加速度峰值200,gal地震激励下，采用不同控制策略的p1墩主梁与墩顶间相对位移Fig.3 The relative displacement between the beam and pier top of p1 using different control strategies by seismic excitation whose peak acceleration is 200,gal

图4 在加速度峰值200,gal地震激励下，采用不同控制策略的p2墩主梁与墩顶间相对位移Fig.4 The relative displacement between the beam and pier top of p2 using different control strategies by seismic excitation whose peak acceleration is 200,gal

从图5和图6中可以看出，在加速度峰值为400,gal的天津波和El-Centro波激励下，两种半主动控制策略下两个桥墩的墩顶与主梁间的相对位移曲线不再相近．从表2可以看到，在加速度峰值为400,gal的天津波激励下，限界最优半主动控制策略下p1和p2墩的墩顶与主梁间的相对位移峰值分别降低37.5%和33.1%，多墩联合控制策略下p1和p2墩的墩顶与主梁间的相对位移峰值分别降低14.6%和14.4%.但是，破坏最严重的桥墩的损伤指数与两个桥墩的损伤指数之差都有很大程度的降低．其中，损伤最严重的桥墩的损伤指数由大于0.6(严重破坏)降低到小于0.6(中等破坏)，使得桥墩的损伤指数得到较好的控制．在加速度峰值为400,gal的El-Centro波激励下，限界最优半主动控制策略下p1和p2墩的墩顶与主梁间的相对位移峰值分别降低28.9%和23.6%，多墩联合控制策略下p1和p2墩的墩顶与主梁间的相对位移峰值分别降低22.7%和13.5%．但是，损伤最严重的桥墩的损伤指数与两个桥墩的损伤指数之差，比限界最优半主动控制策略下分别降低10.5%和56.7%．其中，损伤最严重的桥墩的震害等级由严重破坏降低为中等破坏．这说明采用多墩联合控制的半主动控制算法能有效降低破坏最严重的桥墩的损伤指数，从而使得各桥墩的损伤指数达到平均分配的效果，防止出现一墩破坏引起全桥无法通行的后果．

图5 在加速度峰值400,gal地震激励下，采用不同控制策略的p1墩主梁与墩顶间相对位移Fig.5 The relative displacement between the beam and pier top of p1 using different control strategies by seismic excitation whose peak acceleration is 400,gal

图6 在加速度峰值400,gal地震激励下，采用不同控制策略的p2墩主梁与墩顶间相对位移Fig.6The relative displacement between the beam and pier top of p2using different control strategies by seismic excitation whose peak acceleration is 400,gal

图7 天津波激励下不同控制策略的桥墩损伤演化Fig.7Pier damage evolution using different control strategies by Tianjin wave excitation

从图7和图8中可以看出，当地震加速度峰值为200,gal时，由于桥墩的损伤指数较小，损伤最严重的桥墩的震害等级只是达到轻微破坏，故多墩联合控制策略对桥墩损伤的平均分配效果并不明显，只是使损伤最严重的桥墩的损伤指数略微降低．当地震加速度峰值为400,gal时，从图7(b)和图8(b)中可以看到，两个桥墩的损伤指数曲线明显向中间靠拢，各墩的损伤指数得到了有效的平均分配．这说明在强震作用下，多墩联合半主动控制策略可以有效降低破坏最严重的桥墩的损伤指数．

4 结 论

本文所提出的以多墩损伤平均分配为目的的联合半主动控制策略，适用于多跨连续梁桥的抗震控制．通过对算例的计算和分析，得到如下结论．

(1) 对于多墩连续梁桥，采用基于MR阻尼器的半主动控制方法，可以较好地控制结构的地震响应，但同时会加剧桥墩的损伤，出现损伤分配不均的情况，即出现部分桥墩发生严重破坏、其余桥墩发生轻微破坏的现象．

(2) 中震作用下，本文提出的多墩联合半主动控制策略的控制效果与限界半主动控制策略的控制效果相近，本应破坏最严重的桥墩的损伤指数稍有降低．而随着地震强度的增加，多墩联合半主动控制策略对桥墩损伤平均分配的控制效果也更加明显．

(3) 大震作用下，本文提出的多墩联合半主动控制策略能够在较好地控制连续梁桥地震响应的同时，控制桥墩的损伤指数平均分配，使得破坏最严重的桥墩的损伤指数大幅度降低，抑制了“一处损，全桥断”情况的发生，有利于震后的通行救援．

［1］ 彭天波，李建中，范立础. 双曲面球型减隔震支座的开发及应用 [J]. 同济大学学报：自然科学版，2007，35(2)：176-180.

Peng Tianbo，Li Jianzhong，Fan Lichu. Development and application of double spherical aseismic bearing [J]. Journal of Tongji University：Natural Science，2007，35(2)：176-180(in Chinese).

［2］ 李忠献，岳福青，周 莉. 城市隔震高架桥梁地震反应的半主动控制 [J]. 土木工程学报，2007，40(1)：42-48.

Li Zhongxian，Yue Fuqing，Zhou Li. Semi-active control on seismic responses of vibration-insulated urban elevated bridges [J]. China Civil Engineering Journal，2007，40(1)：42-48(in Chinese).

［3］ Sahasrabudhe S S，Nagarajaiah S. Semi-active control of sliding isolated bridges using MR dampers：An experimental and numerical study[J]. Earthquake Engineering and Structural Dynamics，2005，34(8)：965-983.

［4］ Loh C H，Wu L Y，Lin P Y. Displacement control of isolated structures with semi-active control devices [J]. Journal of Structural Control，2003，10(2)：77-100.

［5］ Erkus B，Abe M，Fujino Y. Investigation of semi-active control for seismic protection of elevated highway bridges [J]. Engineering Structures，2002，24(3)：281-293.

［6］ Iemura H，Igarashi A，Kalantari A. Experimental verification and numerical studies of an autonomous semiactive seismic control strategy[J]. Structural Control and Health Monitoring，2006，13(1)：301-323.

［7］ 姜 南. 应用MR阻尼器的相邻建筑地震反应半主动控制理论与试验研究[D]. 天津：天津大学建筑工程学院，2008.

Jiang Nan. Theory and Experiment on Semi-Active Control of Seismic Responses of Adjacent Buildings Using MR Dampers [D]. Tianjin：School of Civil Engineering，Tianjin University，2008(in Chinese).

［8］ 欧进萍. 结构振动控制——主动、半主动和智能控制[M]. 北京：科学出版社，2003.

Ou Jinping. Structural Vibration Control—Active，Semiactive and Intelligent Control[M]. Beijing：Science Press，2003(in Chinese).

［9］ 姜 南，李忠献，孙松建. 相邻模型结构MR阻尼器半主动控制振动台试验[J]. 天津大学学报，2012，45(1)：58-63.

Jiang Nan，Li Zhongxian，Sun Songjian. Semi-active control of adjacent model structures connected with MR dampers using the shaking table [J]. Journal of Tianjin University，2012，45(1)：58-63(in Chinese).

［10］ 亓兴军，李小军. 桥梁减震半主动控制算法比较与分析[J]. 振动与冲击，2006，25(6)：71-75.

Qi Xingjun，Li Xiaojun. Comparison and analysis of the algorithm of bridge seismic semi-active control[J]. Journal of Vibration and Shock，2006，25(6)：71-75(in Chinese).

［11］ 刘金龙. 地震作用下多塔斜拉桥失效模式控制研究[D]. 哈尔滨：哈尔滨工业大学土木工程学院，2009.

Liu Jinlong. Study of Control for Seismic Damage Modes of Cable-Stayed Bridge with Multi-Tower [D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2009(in Chinese).

［12］ 王东升，冯启民，王国新. 考虑低周疲劳寿命的改进Park-Ang地震损伤模型[J]. 土木工程学报，2004，34(11)：41-49.

Wang Dongsheng，Feng Qimin，Wang Guoxin. A modified Park-Ang seismic damage model considering low-cycle fatigue life [J]. China Civil Engineering Journal，2004，34(11)：41-49(in Chinese).

［13］ Park Y J，Ang A H. Mechanistic seismic damage model for reinforced concrete[J]. Journal of Structural Engineering，1985，111(4)：740-757.

［14］ 胡聿贤. 地震工程学 [M]. 北京：地震出版社，1988.

Hu Yuxian. Earthquake Engineering[M]. Beijing：Seismological Press，1988(in Chinese).

(责任编辑：樊素英)

Continuous Beam Bridge Multi-Pier Joint Semi-Active Control Under Strong Earthquake

Sun Songjian，Jiang Nan，Li Zhongxian
(Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin University，Tianjin 300072，China)

For the purpose of evenly distributing the pier damage of continuous beam bridge，a multi-pier joint semiactive control algorithm is proposed. On the basis of active optimal control，considering the damage state of the continuous beam bridge pier，this control algorithm controls the acceleration of the beam and the relative displacement between the top of each pier and the beam and meanwhile evenly distributes the damage index of each pier by adjusting the target output of dampers. A three-span continuous beam bridge equipped with magnetorheological(MR)dampers is numerically studied with MATLAB and several scenarios are simulated to validate the proposed semi-active control algorithm. The results indicate that the proposed algorithmis well capable of controlling seismic response and effectively reducing the damage index of the pier which suffers the most serious damage，thus achieving the effect that the damage of each pier is evenly distributed.

continuous beam bridge；pier damage；magnetorheological(MR) damper；semi-active control；relative displacement

TU311.3；TU352.1

A

0493-2137(2014)07-0570-07

10.11784/tdxbz201209009

2012-09-05；

2012-11-07.

国家自然科学基金重大研究计划重点资助项目(90715032)；国家自然科学基金国际合作项目(51021140003)．

孙松建（1983— ），男，博士，sunsongjian@163.com.

李忠献，zxli @tju.edu.cn.