基于Kelvin振子的界面摩擦系数计算方法

徐国宾，高仕赵,2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 鲁东大学土木工程学院，烟台 264025)

基于Kelvin振子的界面摩擦系数计算方法

徐国宾1，高仕赵1,2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 鲁东大学土木工程学院，烟台 264025)

为了解决界面摩擦系数计算方法问题，假设接触界面的摩擦能量以声子的形式向外传播，因此接触界面微观振子所耗散的能量等于宏观界面向外传递的热能，应用等效阻尼方法可求出等效黏性阻尼；同时提出了Kelvin振子摩擦耗散模型，通过此模型得到表面能变化的损耗率；最后应用“鹅卵石”模型求出摩擦系数．采用此公式计算的结果与前苏联学者Кpaгeпьcкий等提出的摩擦系数与相对滑动速度试验中极大载荷情况下的摩擦系数变化趋势非常相似．另外，摩擦力计算公式所得数值与Lantz等利用超高真空原子力显微镜研究硅探针在NbSe2试样表面接触和摩擦时的试验结果比较接近．因此证明了此摩擦系数计算公式具有一定的可靠性.

界面摩擦；“鹅卵石”模型；Kelvin振子；摩擦系数

摩擦现象广泛存在于各个领域，据不完全统计，全世界能源的一半左右以摩擦的形式耗散掉．如何降低摩擦、减小能量耗散，是摆在研究者面前的一个重要课题．起初人们认为摩擦是由于摩擦界面粗糙度引起的，但是一些超精加工表面的摩擦系数不但不降低反而剧增，说明在原子级平坦的界面上仍然存在摩擦现象，其对宏观摩擦的影响是不可忽视的．

本文将研究无磨损原子级光滑的界面摩擦，界面摩擦力主要由接触面之间的黏着效应提供．黏着效应是由于分子的活动性和分子力作用使固体黏附在一起而产生滑动阻力．1929年，Tomlinson提出了声子摩擦的概念．20世纪80年代，IBM公司Almaden研究中心的Gary McClelland和美国东北大学的Jeffrey Sokoloff分别重新提出声子摩擦的观点[1-3]．声子摩擦发生在临近表面的原子发生相对滑动的时候，与原子振动有关，这种振动受到界面滑动机械激励，其能量最终以热能的形式耗散．对于受到滑动机械激励作用的原子振动能量的耗散问题，1929年，Tomlinson提出了固体摩擦能量耗散机理的独立振子模型(简称IO模型)，并首次应用此模型从微观角度解释了摩擦现象，阐述了分子摩擦理论．FK模型和FKT模型进一步考虑了界面原子间的相互作用，但它们的能量耗散机理与IO模型是相同的[4]．

摩擦接触界面原子的实际能量状态将影响下一次跳跃时外力所需做的功，因此能量损耗将直接影响到外力做功，同时摩擦能量耗散值还与物体材料的热物理特性相关．然而，这些模型没有考虑能量耗散对接触表面原子振动的影响，并且摩擦能量耗散是一个非常复杂的过程，需要应用简单的宏观量(如热传导系数等)来量度这种复杂的耗散过程，将摩擦宏观和微观现象统一起来．IO模型的耗散机理为：微观表现为摩擦界面原子将储存在界面的变形能以振动能量的形式向外传递，宏观表现为热能从接触表面向外传递．本文采用Kelvin振子模型对这一耗散机理[5-6]做了进一步阐述．

1 理论推导

界面摩擦会产生微观振子．微观振子是指接触界面内的原子级高频振动．本文采用Kelvin振子模型进行描述，如图1所示．物体A表面被简化成具有正弦变化规律的周期势场，物体B表面原子被简化成具有Kelvin模型特性的振子，其中阻尼器用于模拟接触表面原子振动的耗散(如图1和图2所示)．由于接触表面原子阻尼属于非黏性阻尼，因此采用等效黏性阻尼进行简化．等效原则是令非黏性阻尼在一个周期内耗散的能量与等效阻尼在同一周期内耗散的能量相等[7]，即

式中：c为阻尼比例系数；0ω为无阻尼系统的固有频率；θ为振动的初相角；A′为振动的振幅值．

假设摩擦产生的能量损耗全部以热传导的形式耗散掉，物体A为绝热刚体，且局部温升不会改变物体特性[8]．设具有相对运动(或相对运动趋势)的物体B的温度分布按线性分布，其中接触面的温度为T1，远离接触面的一端温度为T0，因而温升为ΔT=T1-T0(如图3所示)，有

式中：D为热量的特征传播长度；QΔ为稳定传热条件下，厚度为D的材料两侧温差为TΔ时，在T′时间内，通过实际接触面积aA所传递的热量；K为热传导系数．

图1 Kelvin振子模型Fig.1 Kelvin oscillator model

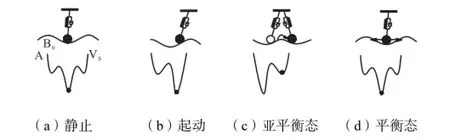
图2 Kelvin振子微观能量损耗机理Fig.2 Micro-energy loss mechanism of the Kelvin oscillator model

图3 散热分析Fig.3 Heat dissipation analysis

根据阻尼等效准则，由式(1)和式(3)得

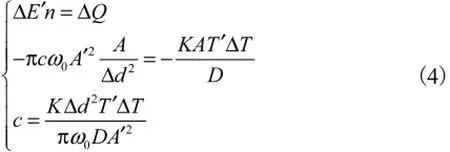
式中n为实际接触面积内所含振子的数量．

为了研究接触面原子能量损耗，取界面原子0B为研究对象(如图4所示)．以原子未受扰动时的平衡位置为坐标原点建立坐标系．图4中，黏性阻尼力cF沿原子速度的反方向，大小为cx˙；比例系数c取式(4)中的等效阻尼比例系数；弹性力kF沿原子速度的反方向，大小为kx．当原子在局部势场的最大值处失稳时，原子做自由振动的方程为

式中m为原子质量．

图4 Kelvin振子受力分析Fig.4 Free body diagram of the Kelvin oscillator model

令式(5)各项除以m，可转化为

式中：δ为阻尼系数；ΔE为原子表面能的变化量．原子微观振动的固有频率为

式中：γ为表面能密度；DΔ、0D和Δd如图5所示．

阻尼系数δ为

令z=eλt，代入式(6)，导出本征方程为式中ζ为阻尼比(δ与ω0的比值)．

本征值为

由于原子振荡的存在，Kelvin原子模型处于欠阻尼状态，式(6)的通解为

式中C1和C2均为待定常数．与无阻尼振动类似，式(12)也可写为式中：A′和θ分别为阻尼振动的初始振幅和初相角；dω为阻尼振动的固有角频率．

由于阻尼作用引起的能量耗散，系统不可能保持等幅的简谐振动，而转变为振幅不断衰减的衰减振动．因此能量耗散率ε为

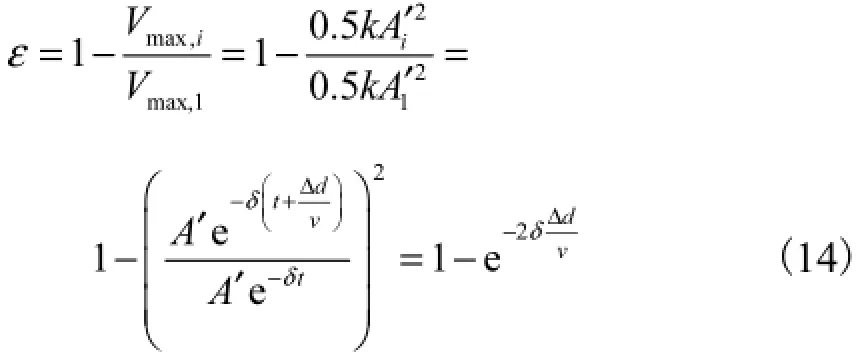
式中v为与接触表面相切的移动速度．

Israelachvili从微观上探讨以能量耗散建立了“鹅卵石”模型．在Israelachvili模型中，物体表面被视为原子级光滑，相对滑动过程被抽象为球形原子，相对滑动过程被抽象为球形原子在规则排列的原子阵表面上的移动，如图5所示．

图5 球形原子在表面的滑动Fig.5 Sliding of the spherical atom on the surface

在滑动过程中，所耗散掉的能量等于摩擦力所做的功，即

Kelvin振子B0以速度v移动Δd所需的时间为t′=Δd/v．将式(4)、(8)、(9)和(14)代入式(15)，可得

对于黏着效应计算公式中的温差ΔT可以用瞬现温度来近似，下面讨论晶格接触面的瞬现温度．假设两个微凸体晶格接触面之间有摩擦，摩擦系数为．晶格接触面之间的温度增长为ΔT，假设在接触时间t中，热量的特征传播长度(即前面提到的材料厚度)远大于接触直径，佩克莱特数

式中α为热扩散率．

这种帮倒忙的方式，是妈妈闯入了孩子的成长空间，并承担了本应该孩子自己承担的责任——因为磨蹭造成的后果。虽然结果是美好的，孩子上学没有迟到，作业按时完成，时间安排紧凑，但每一步都是在妈妈的保护伞下进行的，不是孩子自觉自愿的结果。长此以往孩子就会形成一种思维定式——虽然做事情会被妈妈骂，但只要我装听不到，妈妈什么都会替我做的。长期下去，妈妈只会越来越累，孩子也丧失自己锻炼的机会，不利于独立能力的培养。

在式(17)得到满足的条件下，对于表面上一个给定的热产量，都可以将每一点的瞬时热传播当作一个瞬态过程．

假设微凸体晶格接触面之间的摩擦全部转化为热能，并且总能量仅流到一个物体中，则对于微凸体上的单个晶格，其温升TΔ为

式中：ΔFN为晶格接触面的作用力；σ0为软材料表面的接触硬度；′为变形能摩擦理论的摩擦系数，′=．将ΔFN和f0′代入式(18)，可得[9]式中：G为接触材料的剪切模量；E为接触材料的弹性模量．

将式(19)代入式(16)，可得

摩擦力与法向载荷呈正比，同时根据N0/AFσ≈，可得

2 计算实例

表1 金属相关参数Tab.1 Related parameters of metals

图6 摩擦力vF与实际接触面积A的关系Fig.6 Relationship between friction force and actual contacting area

图7 摩擦力vF与相对滑动速度v的关系Fig.7 Relationship between friction force and relative sliding velocity

另外，图8中摩擦系数vf与相对滑动速度v的关系与前苏联学者Крагепьский等提出的摩擦系数与相对滑动速度试验结果中极大载荷情况的趋势非常相似．由图7可知，摩擦力vF随接触面硬度的减小而降低，这与具有软材料表面膜的摩擦副滑动系数较小的现象相符．通过上面的相关分析可知式(21)具有一定的可信度．

图8 摩擦系数vf与相对滑动速度v的关系Fig.8 Relationship between friction coefficientand relative sliding velocity

3 结 语

由摩擦系数计算公式可知，界面摩擦力随着实际接触面积的增加而增大．这主要是由于接触面积增加，其表面能随之增大，进而导致表面能变化量增大．这是导致摩擦力增大的主要原因．超精加工摩擦面的摩擦系数不但不降低反而增加这一摩擦现象，也是由于实际接触面积增大引起的．同时摩擦系数计算公式也提供了一种降低滑动摩擦系数的方法，即在摩擦表面上应用表面能密度较低的材料可以降低接触表面能，从而降低摩擦系数．当相对滑动速度增加时，摩擦力和摩擦系数减小，这主要归咎于当相对滑动速度提高时，振子在两个势垒之间停留的时间缩短，因此其能量损耗降低，进而导致摩擦力和摩擦系数降低．本文所提出的摩擦系数计算公式能够解释一些摩擦现象，但是还缺乏一些具体的试验数据进行验证．

［1］ 温诗铸，黄 平. 摩擦学原理[M]. 北京：清华大学出版社，2008.

Wen Shizhu，Huang Ping. Principles of Tribology [M]. Beijing：Tsinghua University Press，2008(in Chinese).

［2］ Hiroyuki Tamura，Kazuya Tsujimichi，Hideo Yamano，et al. Molecular dynamics simulation of the friction between talc(001)surfaces[J]. Applied Surface Science，1997，119(3/4)：335-340.

［3］ Demas N G，Timofeeva E V，Routbort J L，et al. Effects of BN and MoS2nanoparticles added to polyalphaolefin oil in piston skirt/cylinder liner tests[J]. Tribology Letters，2012，47(1)：90-102.

［4］ 张 涛，王 慧，胡元中. 无磨损摩擦的原子理论[J]. 摩擦学学报，2001，21(5)：396-400.

Zhang Tao，Wang Hui，Hu Yuanzhong. Models of wearless friction at the atomic scale[J]. Tribology，2001，21(5)：396-400(in Chinese).

［5］ Jiang Hongjun，Meng Yonggang，Wen Shizhu. Effects of external D. C. electric fields on friction and wear behavior of alumina/brass sliding pairs[J]. Science in China：Series E，1998，41(6)：617-625.

［6］ Meng Yonggang，Hu Bo，Chang Qiuying. Control of local friction of metal/ceramic contacts in aqueous solutions with an electrochemical method[J]. Wear，2006，260(3)：305-309.

［7］ 刘延柱，陈文良，陈立群. 振动力学[M]. 北京：高等教育出版社，1998.

Liu Yanzhu，Chen Wenliang，Chen Liqun. Vibration Mechanics[M]. Beijing：Higher Education Press，1998(in Chinese).

［8］ 许中明，黄 平. 摩擦微观能量耗散机理的复合振子模型研究[J]. 物理学报，2006，55(5)：2427-2432.

Xu Zhongming，Huang Ping. Composite oscillator model for the energy dissipation mechanism of friction [J]. Chinese Journal of Physics，2006，55(5)：2427-2432(in Chinese).

［9］ 波波夫 瓦伦丁 L. 接触力学与摩擦学的原理及其应用[M]. 李 强，雒建斌，译. 北京：清华大学出版社，2011.

Popov V L. Contact Mechanics and Friction Physical Principles and Applications[M]. Li Qiang，Luo Jianbin，Trans. Beijing：Tsinghua University Press，2011(in Chinese).

［10］ 许中明，黄 平. 考虑接触界面材料微观结构与势能参数的滑动摩擦计算研究[J]. 摩擦学学报，2006，26(2)：159-163.

Xu Zhongming，Huang Ping. Calculating friction force with considering material microstructure and potential on contact surfaces[J]. Tribology，2006，26(2)：159-163(in Chinese).

（责任编辑：金顺爱）

Calculation Method of Interfacial Friction Coefficient Based on Kelvin Oscillator

Xu Guobin1，Gao Shizhao1,2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. School of Civil Engineering，Ludong University，Yantai 264025，China)

In order to solve the problem of the calculation method of the interfacial friction coefficient, it was assumed that the energy of the contact interface spread in the form of a phonon, and therefore the energy dissipated by the micro-oscillator on contact interface is equal to the heat which is passed by the macro-interface. The equivalent damping method was applied to calculate the viscous damping. The Kelvin oscillator friction dissipation model was proposed, and by this model, the loss rate of the surface energy was obtained. Finally, the “cobblestone” model was applied to calculate the friction coefficient. There is a very similar trend between the result calculated by this formula andthe test result proposed by the former Soviet Union scholar Крагепьский et al in the great load test of the friction coefficient with the change of relative sliding velocity. In addition, the results conform to the test result which has been proposed by Lantz, using the ultra-high vacuum atomic force microscopy (AFM), in the process of Lantz's studies of the contact and friction of the silicon probe on the NbSe2specimen surface. Therefore, the formula of the friction coefficient is proved to have certain reliability.

interfacial friction；“cobblestone” model；Kelvin oscillator；friction coefficient

O313

A

0493-2137(2014)07-0565-05

10.11784/tdxbz201211065

2012-11-27；

2013-01-09.

国家自然科学基金创新研究群体科学基金资助项目(51021004)；国家自然科学基金资助项目(50979067)；鲁东大学博士启动基金资助项目.

徐国宾（1956— ），男，教授.

徐国宾，xuguob@sina.com.