基于控制系数的交通信号动态配时研究

包晓安，胡 星，张 娜，顾小卫，桂 宁

（浙江理工大学信息学院，杭州310018）

基于控制系数的交通信号动态配时研究

包晓安，胡 星，张 娜，顾小卫，桂 宁

（浙江理工大学信息学院，杭州310018）

为缓解城市路口处的交通拥挤状况，针对路口多相位交通流建立一种实时动态模型，提出一种基于控制系数的交通信号配时方法。用随机的交通流数据模拟路口各个车道上监测到的车辆数目，在以各个相位对应车道上的车辆数目按照比例分配相位时间的基础上，提出车辆资源竞争公平性问题，引入控制系数，以最大通行能力为路口模型控制性能指标，进行周期信号灯配时的仿真。仿真结果表明，此方法比定时控制方法提高了1.7%的通行率，对于路口的信号控制是行之有效的。

交通流；控制系数；相位时间；信号控制；动态配时

0 引 言

交通是城市经济活动的命脉，对城市的发展产生重大的影响，交通的畅通与否与人们的生活息息相关。在现代城市的高速发展下，车辆保有量日益增多，人们生活节奏越来越快，对于城市的交通服务要求不断提高，交通拥挤会增加出行者的出行时间，提高汽车尾气排放量，造成社会经济损失和环境生态污染。而路口在交通运行中担任着重要作用，是交通车辆的汇聚地。交通信号灯又是交叉路口必不可少的交通控制手段，所以城市交通路口处信号配时的研究对于人们的生活意义十分重大。

交叉路口信号控制的历史由来已久。国内外学者为提高交叉口的通行效率，做过不懈地努力并提出了很多方法［1-7］。2001年，黄辉先等［4］运用遗传算法实时分配相位时间，对路口的时间分配进行优化，提高了车辆通行率。2003年，高海军等［5］基于先放行所在车道车辆数最多的方法，灵活调节相位顺序、相位时间以及相位组合。之后，Karakuzu等［7］用硬件实现了交叉口处各方向的红绿黄信号灯，并用模糊控制对信号灯的信号配时进行智能地、实时动态调节。近几年，还有很多人将智能控制算法，如遗传算法用于对交通路网的控制并取得了不错的效果［8-10］。

一直以来，交通信号的控制都是研究的热点，现在大多学者都是运用人工智能控制的方法实现路口交通流数据的自适应控制，提高通行能力，减少延误时间。本文提出了一种信号配时的方法，主要是在各相位对应车道上的车辆数目按照比例分配相位时间的基础上，引入控制系数进行加权，重新分配相位时间，从而取得对各个周期信号配时的结果。

1 交叉路口交通流数学模型

交叉路口的交通流数学模型分布如图1所示，一个路口有东南西北4个方向，每个方向上均存在着左转，直行，右转的车辆，每一个方向上都可以简化为3个车道。通过对路口各个车道车流量进行实时检测，从而获取车流量信息，由于车流量是随机变化的，很难用数学方法描述其规律，本文采用随机矩阵模拟车道上的车流量实时数据，以路口流通能力最大，即排队长度最小为优化目标函数，对相位进行信号配时。

图2所示为单交叉路口四相位信号控制的交通图。本文只考虑路口车道上左转和直行的车辆是否允许通行，因为左转和直行是可能产生冲突的交通流，为保证安全，所以需要将产生冲突的车流分配到不同相位上，右转是常绿状态。针对一个四相位不断交替运行的交叉路口，为了表示不同相位，不同车道上的车辆放行状态，引入一个系数矩阵pe。

图1 单交叉路口

图2 四相位交通

式（1）中：i为相位序号，取值为1，2，3，4，分别表示第一，第二，第三，第四相位；j表示路口的方向，取值为1，2，3，4，分别表示东、南、西、北方向；k为车道序号，取值为1，2，3，分别表示左转、直行、右转车道；

对于图2中四相位的交通图，放行状态控制系数矩阵为：

设：tni（i=1，2，3，4）为交叉路口第n个周期，第i个相位的信号配时；λnijk为第n个周期、第i个相位、第j个方向、第k个车道上的车辆到达率，则可以得出第n个周期中、第i个相位、第j个方向、第k个车道上的车辆到达数目为

记第n个周期、第i个相位的车辆到达矩阵为

假设在绿灯期间内，unijk为放行车辆在第n个周期、第i相位、第j个方向、第k个车道上的车辆离开率，则在第n个周期、第i相位、第j个方向、第k个车道上的车辆离开数目

记第n个周期、第i个相位的车辆离开矩阵为

式（7）中，i=1，2，3，4；j=1，2，3，4；k=1，2，3。

记第n个周期、第i个相位结束时，车辆数目矩阵为，

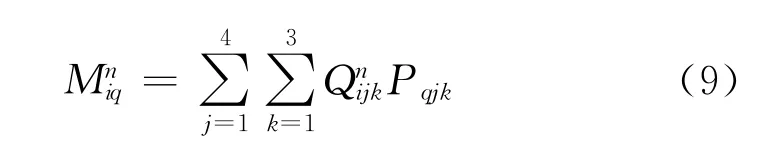
式（9）中i=1，2，3，4；j=1，2，3，4；k=1，2，3。

为了使路口通行能力达到最大，路口上滞留车辆数目最少，满足

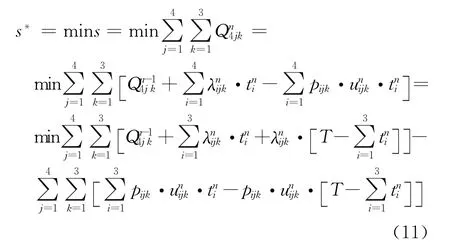
优化过程也就是对路口各个周期的4个相位进行实时分配相位时间，在固定周期T的约束下，各个相位的时间满足

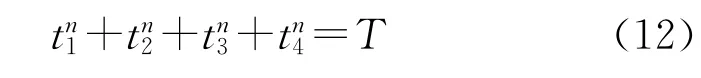
考虑到行人过马路以及车辆启动时间等，每一相位设定一个最短时间e（这里e取10 s），因此每一个相位的配时必须满足

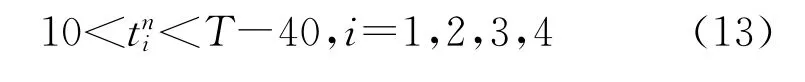
2 算法优化动态配时控制

路口处相位的时间分配主要是由路口上的交通流分布决定的，与路口各个时刻各个车道到达的车辆数目，以及由各相位各车道上的滞留车辆数目都密切相关。本文中，设定的路口下一个相位时间是由当前相位结束时，车辆数目矩阵计算得到的。为保证相位不出现空放现象，每个相位的时间不小于e，定义第n个周期、第i相位时间为：

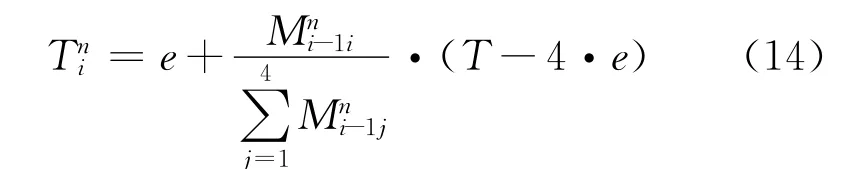
计算第n个周期、第i相位的时间，根据式（14）可以看出是由第n个周期、第i-1相位绿灯时间结束以后矩阵车辆数目矩阵进行计算的，这样就导致此时第n个周期、第i-1相位绿灯车道上对应的车辆数目相对来说是最少的，很有可能为0，为了保证在后面一个周期上对前面一个相位分配时间的公平性，也就是在第n+1个周期、个相位上的时间分配合理性和公平性，需要引入加权系数ω对前一个相位的车辆数目进行加权等价当前绿灯结束时所在车道上的车辆，将此加权系数ω定义为控制系数。式（14）应该修正为：

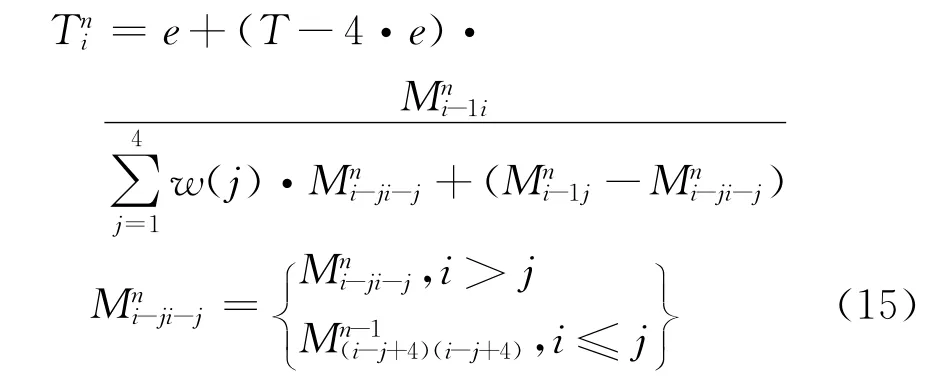
依据以上分析，可以得到计算方法如下：

a）依据车辆数目矩阵确定当前相位时间；

b）依靠随机矩阵生成在当前相位时间内的车辆平均到达率，计算得到各个车道上的车辆数目；

c）根据相位时间以及当前相位，计算离开的车辆数目矩阵；

d）保存当前相位对应的车道上的车辆数目总和；

e）引入控制系数，根据式（15）计算下一相位的时间；

f）判断仿真周期是否已经完成，没有，则将下一相位赋值为当前相位，转至步骤a）；否则结束。

程序流程图的步骤如图3所示。

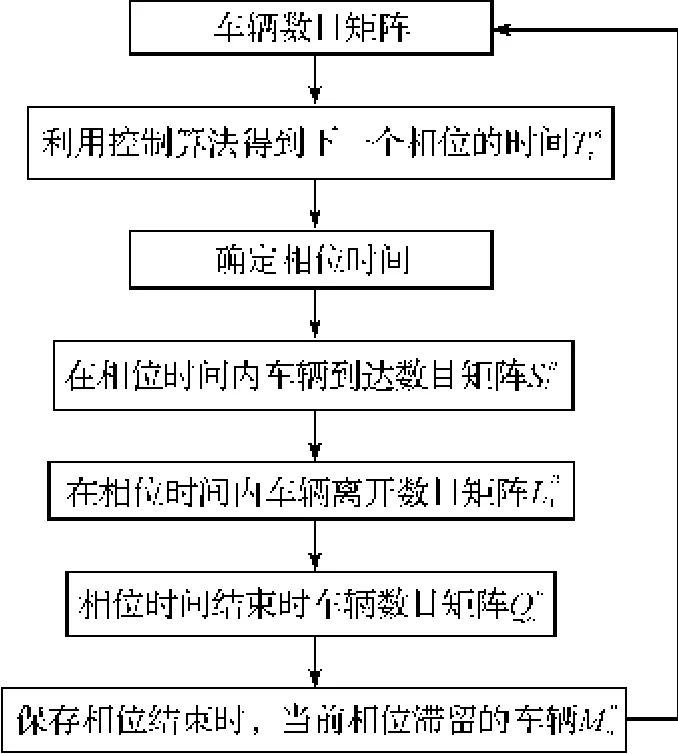
图3 仿真流程图

3 仿真研究

单路口交通信号配时控制算法采用Matlab进行编程，在路口东、南、西、北方向的左转、直行、右转车辆可以由平均车辆到达率进行模拟，平均车辆到达率利用Matlab中的rand（4，3）进行编写得到。能较好地模拟现实生活中的车辆运行情况。

路口各个方向各个车道上通行时车辆通过率为1辆/s，固定周期时间T=100 s，仿真程序采用设计的算法和传统定时算法进行计算，比较10个周期的通行情况，通过计算，结果如表1所示。

m表示每个周期，路口各个方向，各个车道在绿灯时，通过总的车辆数目。表格1中给出了10个周期，4个相位的时间分配，对比了定时控制和本文算法中通行量m参数的情况，得出了两种控制算法下的相位时间调配以及在多个周期内通过的车辆数目m。因为车辆到达率是采用随机均匀分布的，所以定时控制在每个相位分配的时间都是25 s，可以看出，大多数周期上，本文算法都比定时控制算法有着优势。通过的车辆数都多于定时控制。

从Matlab仿真图中（图4）可以更清楚地观察10个周期中本文算法和定时算法的车辆到达、车辆离开、车辆滞留车道上的情况，大多数情况下本算法通过的车辆数都多于定时控制，在滞留的车辆数上，定时控制都要多于本文设计的算法。

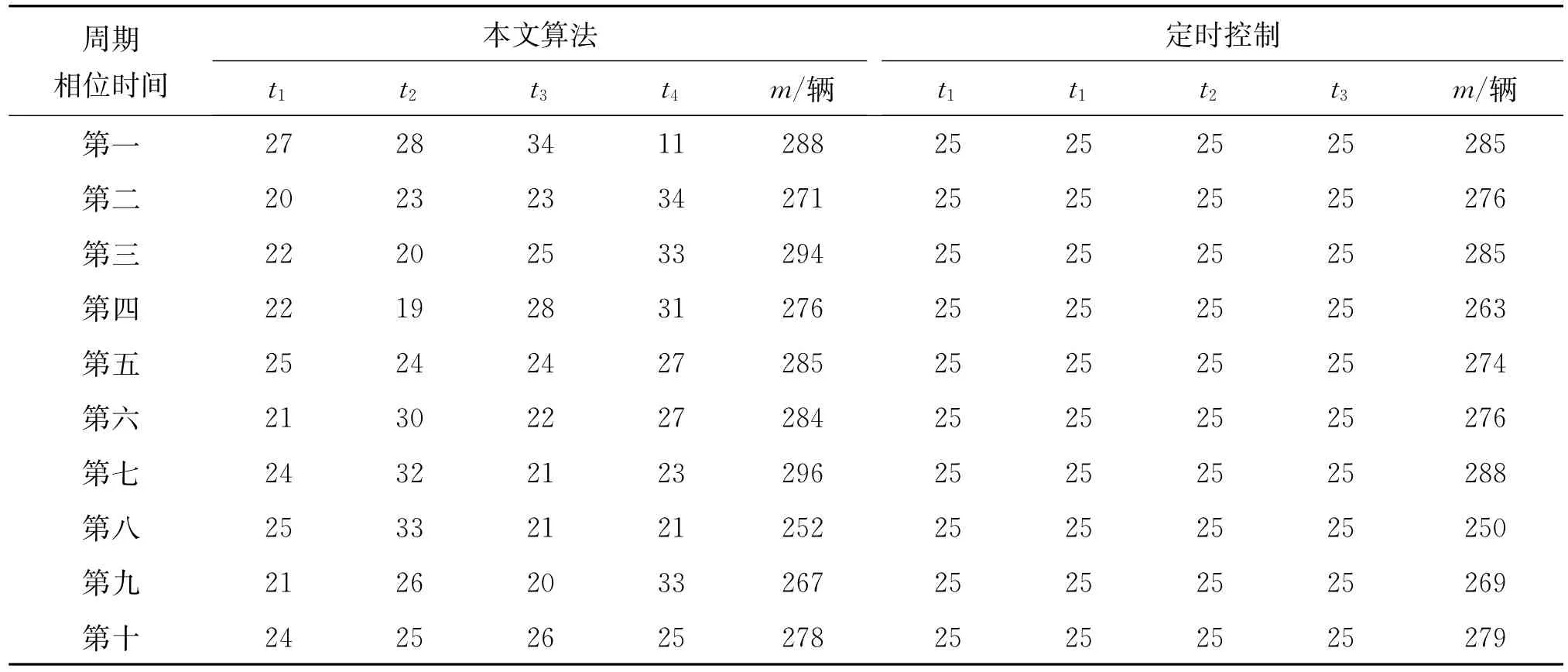
表1 定时控制与本文算法比较 单位：s

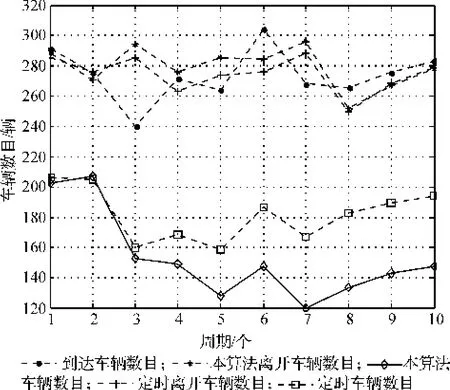
图4 定时算法和设计算法比较仿真图

4 结 语

本文以平面交叉路口为研究对象，用随机矩阵模拟检测到的车辆数为输入，综合考虑了当前相位车辆数在所有车道上所占的比例进行配时。为了保证公平性，减少车辆等待时间，引入了加权系数，使得路口上的配时更加合理。仿真结果表明，提出的方法是有效的。该算法比较简单，不需要经过大量的计算，具有较好的实时性，操作起来更加方便，可以扩展到可变周期上进行控制。后续工作上需要学习一些人工智能算法，并将这些算法的优点相结合，应用到多路口的动态配时研究中。

［1］徐冬玲，方建安，邵世煌.交通系统的模糊控制及其神经网络实现［J］.信息与控制，1992，21（2）：74-79.

［2］陈 洪，陈森发.单路口交通实时模糊控制的一种方法［J］.信息与控制，1997，26（3）：68-74.

［3］刘智勇，朱 劲.单交叉口的多相位模糊控制［J］.信息与控制，1999，28（6）：453-458.

［4］黄辉先，史忠科.城市单交叉路口交通流实时遗传算法优化控制［J］.系统工程理论与实践，2001，21（3）：102-106.

［5］高海军，李灵犀，陈 龙.交通路口可变相位信号控制［J］.交通运输工程学报，2003，3（3）：79-83.

［6］赵忠杰，刘小强，谢光秋.单交通路口变相位变周期信号控制［J］.长安大学学报：自然科学版，2005，25（6）：70-72.

［7］Karakuzu C，Demirci O.Fuzzy logic based smart traffic light simulator design and hardware implementation［J］. Applied Soft Computing，2010，10（1）：66-73.

［8］Zhao D，Dai Y，Zhang Z.Computational intelligence in urban traffic signal control：a survey［J］.Systems，Man，and Cybernetics，Part C：Applications and Reviews，IEEE Transactions on，2012，42（4）：485-494.

［9］Zhang L，Yin Y，Chen S.Robust signal timing optimization with environmental concerns［J］.Transportation Research Part C：Emerging Technologies，2013，29：55-71.

［10］Schmöcker J D，Ahuja S，Bell M G H.Multi-objective signal control of urban junctions-framework and a London case study［J］.Transportation Research Part C：E-merging Technologies，2008，16（4）：454-470.

Research on Traffic SignaI Dynamic Timing Based on ControI Coefficient

BAO Xiao-an，HU Xing，ZHANG Na，GU Xiao-wei，GUI Ning
（The School of Information Science and Technology，Zhejiang Sci-Tech University，Hangzhou 310018，China）

In order to alleviate urban traffic congestion at the junction，a real-time dynamic model in allusion to multiphase traffic flows is set up.This paper proposes a traffic signal timing method based on control coefficient.The number of vehicles detected in every lane is simulated by random traffic flow data. On the basis of allocating phase time according to the proportion for the number of vehicles on the corresponding lane of each phase，this paper put forward vehicle resource competition justice，introduces control coefficient and simulates periodic signal lamp timing with the maximum traffic capacity as intersection model control performance index.The simulation results show that this method improves 1.7%traffic rate compared with the timing control method and it is effective for intersection signal control.

traffic flow；control coefficient；phase time，signal control；dynamic timing

TP391.9

A

（责任编辑：陈和榜）

1673-3851（2014）05-0517-04

2014-02-18

国家自然科学基金（61202050，61379036，11347125）；浙江省自然科学基金（LY12F02041，Y13F020175）；浙江省钱江人才计划项目（2013R10064，2012R10009）；浙江理工大学521人才培养计划，浙江省新苗计划项目（2012R406071，2013R406070，2014R406073）

包晓安（1973-），男，浙江东阳人，教授，主要从事智能交通、自适应软件及软件测试等领域研究。

张 娜，E-mail：zhangna@zstu.edu.cn