低照度视频监控图像降噪算法设计与实现
2014-06-02刘磊磊蒋荣欣
刘磊磊,蒋荣欣
低照度视频监控图像降噪算法设计与实现
刘磊磊,蒋荣欣
(浙江大学浙江省网络多媒体技术研究重点实验室,杭州 310027)
针对低照度环境下视频监控图像噪点较多的问题,提出一种基于运动检测的低照度视频监控图像降噪算法。在研究低照度视频监控图像噪声特点的基础上,通过一种阈值运动检测算法将图像帧划分成8×8的运动像素宏块和静止像素宏块,对运动像素宏块采用改进的维纳滤波算法进行降噪,对静止像素宏块采用数学形态学和中值滤波相结合的算法进行降噪。实验数据显示,该算法总体时间复杂度接近(),使用该算法降噪后的图像的PSNR值和DV/BV值均高于经典降噪算法,证明了该算法在降低时间复杂度的同时,能有效降低图像噪声,并较好地保持图像的解析度。
低照度;图像降噪;运动检测;数学形态学;中值滤波;维纳滤波
1 概述
目前,视频监控系统对图像低噪声、高解析度和高实时性提出了更高的要求。然而,在低照度(照度<1.0Lux)环境下,电荷耦合器件(Charge Coupled Device, CCD)摄像机在提高传感器增益以增强光信号强度的同时也放大了噪声,所以采集到的图像往往噪点很多[1]。
传统的频域降噪算法复杂度很高,空域降噪算法存在降噪效果不佳或者容易引起图像模糊的问题。基于小波变换和偏微分方程理论的降噪算法的研究是近年来的热点。文献[2]提出的邻域阈值萎缩(NeighShrink)法以及文献[3]方法都是对小波软硬阈值降噪法的改进,其核心问题是选取合适的阈值函数。文献[4]提出的基于对数图像处理(Logar- ithmic Image Processing, LIP)的偏微分方程降噪模型结合了LIP模型[5]和全变分(Total Variation, TV)模型。这些算法在降噪效果上有很大改进,但是复杂度都较高,不能满足监控系统高实时性的要求。
本文在研究低照度视频监控图像噪声特点的基础上,综合考虑图像降噪效果、图像解析度和算法复杂度,提出一种基于运动检测的降噪算法。该算法通过运动检测,对运动像素宏块使用改进的维纳滤波降噪算法,并对静止像素宏块使用数学形态学和中值滤波法相结合的降噪算法。
2 低照度视频监控图像噪声特点分析
图像中的噪声主要有以下3类[6],在不同环境下都有可能成为影响图像质量的主导噪声。
(1)脉冲噪声:该类噪声主要是图像传输和存储过程中产生的。脉冲噪声主要由电路中电荷活动情况决定,与客观环境的照度无关。
(2)量化噪声:该类噪声是摄像机使用放大和处理电路对信号进行采样和量化处理时产生的。放大电路输出信号信噪比公式如下:
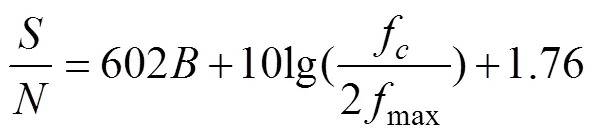
其中,是数模转换器的分辨率;f为采样速率;max是最高的输入信号频率。由式(1)可知,量化噪声与客观环境照度无关。
(3)随机噪声:该类噪声主要是CCD摄像管的读出噪声。读出噪声是一种加性噪声,主要是在图像传感器光电转换中产生的。在低照度情况下,读出噪声模型服从泊松密度分布。
CCD摄像管的读出噪声输出信噪比公式如下:
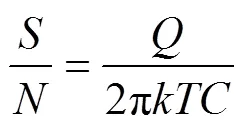
其中,是一个光敏单元存储的电荷量;是输入电容;表示绝对温度。与客观环境光线强度相关,光线充足时会相应增大,所以在低照度环境下图像的信噪比会降低,图像的读出噪声比较严重。
由此可见,低照度视频监控图像中的主导噪声是CCD摄像管摄像产生的读出噪声。
3 低照度视频监控图像降噪算法
3.1 算法整体框架
本文设计的低照度视频监控图像降噪算法流程如图1所示。
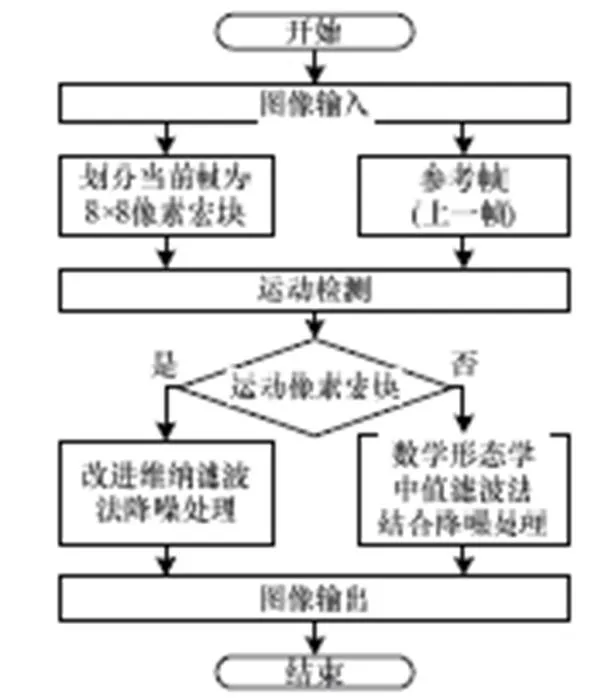
图1 低照度降噪算法流程
输入图像被划分成8×8的像素宏块,与缓存的参考帧(上一帧)一起经过运动检测算法被判定为运动宏块或者是静止宏块。
空域降噪算法应用于运动图像时,或是对摄像管的读出噪声降噪效果很差,或是容易引起图像模糊,所以,本文对运动宏块使用了改进的维纳滤波法进行降噪。维纳滤波可以很好地保留图像高频部分的图像细节信息。本文对维纳滤波进行了改进,对图像的高频部分进行了屏蔽,然后再进行滤波,更好地保留了图像的细节信息。
对静止宏块使用数学形态学和中值滤波法相结合的方法进行降噪。数学形态学降噪效果较差,但是由于开/闭运算具有聚类功能,图像信息不易丢失;中值滤波法降噪效果较好,但是由于低照度图像中噪声与图像信息亮度值差别很小,降噪同时会丢失较多的图像信息。所以,先使用数学形态学去除部分噪声,并将图像细节信息聚集;再使用中值滤波法滤除剩余噪声,这时由于图像信息相对集中,去除噪声时可以避免丢失大量图像信息。
维纳滤波法的时间复杂度为(lb),在频域算法中是比较低的[7];数学形态学和中值滤波法相结合的算法的时间复杂度为()。由于运动宏块在监控图像中相对很少,因此该算法总体时间度接近()。
3.2 运动检测
本文设计的运动检测算法如下:将当前帧划分为8×8的像素宏块,像素宏块中每一个像素与参考帧(上一帧)相应位置像素的值做差,并得到所有像素处理后的差方和。设置一个阈值,若差方和大于阈值认为该像素宏块是运动宏块,否则认为是静止宏块。阈值的选择是该算法的核心问题[8]。
差方和表达式如下:
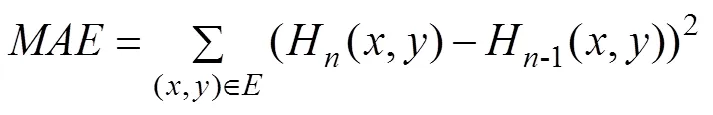
其中,表示差方和;表示8×8像素块;表示灰度值。
对大量视频监控图像分析发现,由于相邻两帧图像之间背景相同,其大部分像素宏块是静止宏块。静止像素宏块的比例一般都在80%以上,只有少数场景(如繁忙的高速)运动像素宏块的比例会接近30%,很多场景(如深夜的街道)静止像素宏块的比例高达95%以上。大量实验发现当运动阈值为15时,运动判定效果较好。
3.3 改进的维纳滤波降噪
一般用统计学上的均值和方差来描述噪声。噪声的均值体现了噪声的总强度,噪声的方差体现了噪声的分布情况。若(,)表示图像信号的二维灰度分布,(,)表示噪声,、表示图像的行列数,其噪声的均值和方差表达式如 式(4)和式(5)所示。
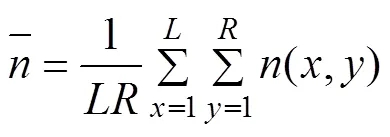

降噪后图像(,)与(,)的方差最小是维纳滤波的基本思想[9]。本文对维纳滤波法进行了改进,先对图像边缘细节相对集中的高频部分进行屏蔽,避开了对图像物体边缘的平滑处理,然后再进行降噪滤波处理,从而减少了图像物体边缘模糊的现象。
由于图像的不规则性,本文对图2所示的9个模板覆盖的像素进行处理,其中图2(a)包含了4个对称的屋形模板,图2(b)包含了4个对称六边形的模板,图2(c)包含了1个正方形的模板,黑色像素点是9个模板覆盖的所有像素的中心像素点。先计算每个模板方差以及9个模板的方差均值,并得到其比值,再用该比值、模板的平均灰度以及当前像素的灰度一起求出一个新的像素值,最后对含有噪声的像素点用该新的像素值进行修正。
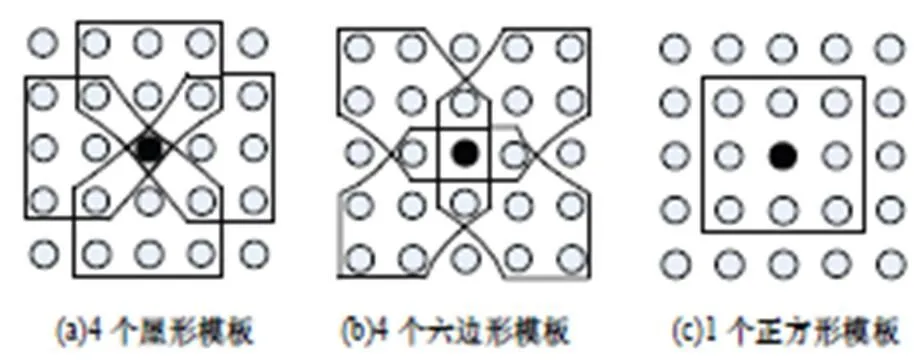
图2 9种不同形状模板
算法具体设计如下:
(1)计算图2所示9个模板包含的所有像素点的灰度值的平均值、9个模板各自包含的像素点的灰度值均值和方差。然后对像素值和模板方差进行修正:当前模板像素修正值=当前像素值–当前模板像素的灰度均值;当前模板方差修正值=当前模板方差–所有模板方差的平均值。
(2)计算各个模板噪声功率系数。其计算公式如下:

(3)对所有需要进行降噪的像素点进行相同的处理。
3.4 数学形态学和中值滤波法相结合的降噪
数学形态学和中值滤波法相结合的降噪过程如下:
(1)对YUV图像的灰度值(即分量)进行数学形态学滤波。
若给定数学形态学结构元素的二值模板(,)和二值图像(,),那么腐蚀和膨胀运算表达式[10]如下:


在此基础上,开运算和闭运算定义如下:让结构元素沿着(,)滚动,开运算沿着(,)的下沿滚动,闭运算沿上沿滚动。经过开闭运算之后,可以去除所有直径小于结构元素的灰度阶越点。
低照度视频监控图像主要是随机的细小亮点和毛刺,可以使用开运算进行处理,即选择直径略大于噪声的结构元素,先对图像进行腐蚀运算来去除亮点和毛刺,再进行膨胀运算增加图像的亮度。噪声的直径是比较小的,所以本文选择3×3结构元素窗口。
(2)对分量进行中值滤波。
若有一个序列1,2,···,f,滑动窗口长度为(取奇数),中值滤波时就是从序列中选择f–t,···,f–1,f,f1,···,f;f是窗口中心的值,其中=(–1)/2。那么滤波输出就是该个值的中值。中值滤波的表达式[11]如下:
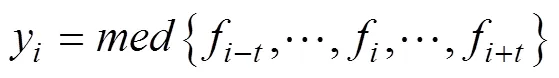
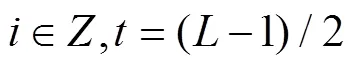
由于数学形态学滤波把图像信息聚集到了一起,再使用中值滤波去除噪声时避免了大量图像细节的损失。为了保证降噪效果,本文选择了3×3滑动窗口。
4 实验结果与分析
该算法已经使用在作者所在视频监控项目中,用于解码之后图像的降噪。本文选择了视频监控系统在低照度环境下的2段具有代表性的监控录像进行实验分析。监控图像1和监控图像2分别是深夜安静的马路(没有运动物体)和夜晚城市高架(有较多运动的行人和车辆)。
实验时各参数的选择如表1所示。

表1 实验参数
同时实验对比了数学形态学、中值滤波法和维纳滤波法降噪效果、图像解析度和时间复杂度。实验结果如图3和图4所示。
从实验结果可以看到数学形态学法虽然保持了较好的图像解析度,但是降噪效果不明显;中值滤波法降噪效果较好,但是会引起运动物体边缘模糊;维纳滤波法降噪效果和保持图像解析度方面表现都不错;本文方法降噪效果明显且保持了图像具有较高的解析度。

图3 监控图像1实验结果

图4 监控图像2实验结果
在图像客观评价中,峰值信噪比(Peak Signal to Noise Ratio, PSNR)用来评价降噪效果好坏,细节方差(Detail Variance, DV)-背景方差(Background Variance, BV)比[12]常用来评价图像边缘和细节是否丰富。PSNR越高,说明图像噪声越少,DV/BV越高说明图像解析度越高。针对图3和图4的客观评价结果如表2和表3所示。
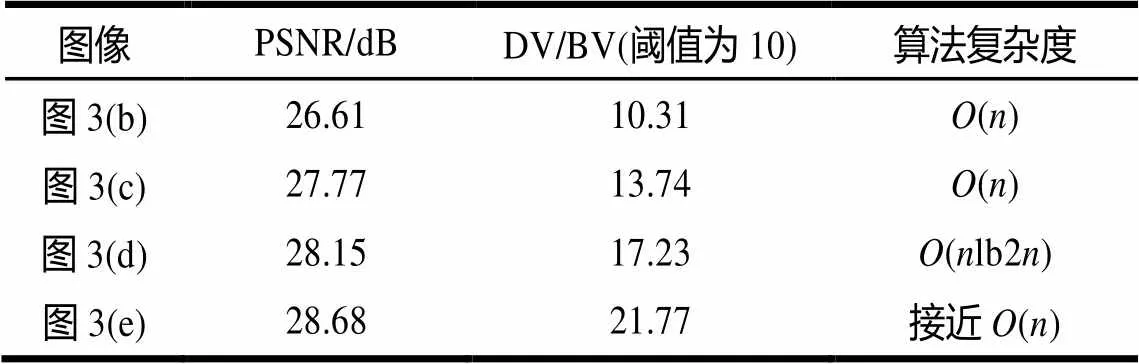
表2 监控图像1实验结果客观评价
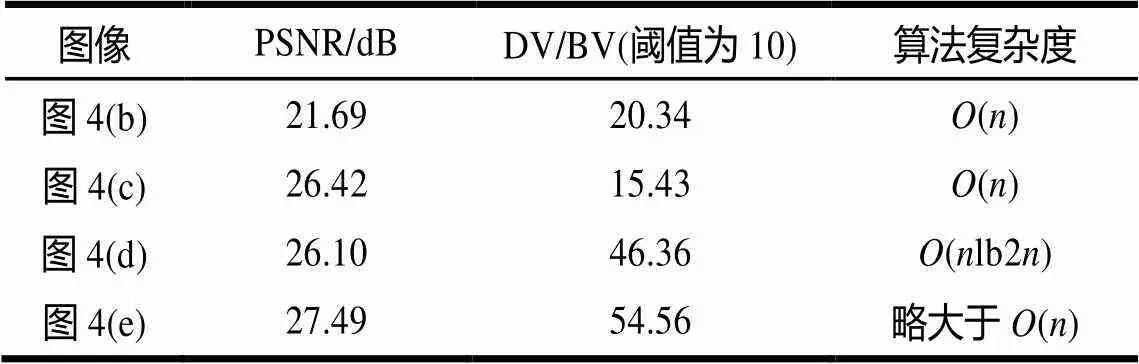
表3 监控图像2实验结果客观评价
根据运动检测算法,可以计算出图3中各图运动像素宏块比例为1.3%;图4中运动像素宏块比例为7.6%,所以,本文算法的复杂度接近于()。由客观评价结果可知本文方法无论是在降噪效果(PSNR值)和保持解析度方面(DV/ BV值)都要优于其他降噪方法。此外,时间复杂度比起一般空域滤波降噪算法提高不多,比较适合用于视频监控图像的实时降噪处理。
5 结束语
本文设计并实现了一种适用于低照度视频监控图像的降噪算法。该算法兼顾了降噪效果、图像解析度以及算法时间复杂度。实验表明经过该算法降噪的低照度视频监控图像的PSNR和DV/BV值都较高,说明降噪之后图像噪声低,解析度高;由于只有少数运动像素宏块使用了复杂度较高的改进的维纳滤波算法,因此该算法复杂度较低,符合监控系统实时性高的要求。今后主要改进工作是针对运动宏块设计复杂度较低的降噪算法,以降低算法的整体复杂度,更好地达到监控系统高实时性的要求。
[1] Liu Xiuping. Impulsive Noise Removal by Nonlocal Fuzzy Diffusion[C]//Proc. of the 4th International Conference of Image and Graphics. Chengdu, China, [s. n.], 2007: 155-159.
[2] Chen Guangyi, Bui T D, Krzyzak A. Image Denoising Using Neighbouring Wavelet Coefficients[J]. Integrated Computer- Aided Engineering, 2005, 12(1): 99-107.
[3] 王传鑫, 邵 诚, 韩 瑜. 基于蚁群算法的小波降噪双阈值优选方法[J]. 控制与决策, 2011, 17(1): 163-165.
[4]Collins R T. Mean-shift Blob Tracking Through Scale Space[C]//Proc. of Conference on Computer Vision and Pattern Recognition. Washington D. C, USA: IEEE Computer Society, 2003: 18-20.
[5] 彭宁嵩, 杨 杰, 刘 志, 等. Mean-Shift跟踪算法中核函数窗宽的自动选取[J]. 软件学报, 2005, 16(9): 1542-1550.
[6] 彭 波, 王一鸣. 低照度图像去噪算法的研究与实现[J]. 计算机应用, 2007, 27(2): 17-21.
[7] Adikari A, Fernando W, Weerakkody W. Side Information Improvement in DVC with Two Side Information Streams and 3D Motion Refinement[C]//Proc. of Canadian Conference on Electrical and Computer Engineering. Vancouver, Canada: Electrical and Computer Engineering, 2007: 32-35.
[8] Zhai Jiefu, Yu Keman, Li Shipeng. A Low Complexity Motion Compensated Frame Interpolation Method[C]//Proc. of IEEE International Symposium on Circuits and Systems. Kobe, Japan: IEEE Press, 2005: 4927-4930.
[9] Wang Lipo, Rajapaksej C, Fukushima K. Speckle Reduction Using Wiener Filtering in Wavelet Domain[C]//Proc. of the 9th International Conference on Neural Information Processing. Singapore: IEEE Computer Society, 2007: 792-795.
[10] 蔡 超, 刘买利, 丁明跃, 等. 一种基于偏微分方程的形态学边缘检测新方法[J]. 华中科技大学学报: 自然科学版, 2003, 34(10): 36-39.
[11] Award M, Chehdi K, Nasri A. Multi-component Image Segmentation Using a Hybrid Dynamic Genetic Algorithm and Fuzzy C-means[J]. IET Image Processing, 2009, 3(2): 52-62.
[12] Xu Zhiyuan, Liu Xiaoming. Fog Removal from Color Images Using Contrast Limited Adaptive Histogram Equalization[C]// Proc. of Image and Signal Processing. Dalian, China: [s. n.], 2009: 1-5.
编辑 金胡考
Design and Implementation of Noise Reduction Algorithm for Low-light Video Surveillance Image
LIU Lei-lei, JIANG Rong-xin
(Key Laboratory of Network Multimedia Technology of Zhejiang Province, Zhejiang University, Hangzhou 310027, China)
For strong noise of low-light video surveillance image, a new image noise reduction algorithm based on motion detection is proposed. The property of the noise of low-light video surveillance image is studied and the image is divided into 8×8 motion pixels blocks and still pixels blocks by a kind of threshold motion detection algorithm. An improved Wiener filter is designed and implemented for noise reduction of motion pixels blocks. The compact algorithm of mathematical morphology and median filtering for noise reduction of still pixels blocks is designed. Experimental results show that the time complexity of the algorithm is about() and the value of PSNR and DV/BV of image after noise reduction is higher than other algorithms. This proves the time complexity of the image noise reduction algorithm is low, while the image noises are well reduced and there is little loss in the resolution of image.
low-light; image noise reduction; motion detection; mathematical morphology; median filtering; Wiener filtering
1000-3428(2014)03-0266-04
A
TP391
国家“863”计划基金资助项目“相控阵三维声学摄像声纳信号处理系统”(2010AA09Z104)
刘磊磊(1988-),男,硕士研究生,主研方向:网络多媒体技术;蒋荣欣,副研究员
2013-03-05
2013-04-10 E-mail:zjuliull@163.com
10.3969/j.issn.1000-3428.2014.03.056
