一种基于有序二元决策图和布尔函数性质计算网络可靠性的算法
2014-06-02王宏祥赵子岩
熊 飞 乔 迪 王宏祥 赵子岩 杨 洪 沈 亮
一种基于有序二元决策图和布尔函数性质计算网络可靠性的算法
熊 飞*①乔 迪②王宏祥②赵子岩①杨 洪①沈 亮①
①(国家电网公司信息通信分公司 北京 100761)②(北京邮电大学信息与通信工程学院 北京 100876)
有序二元决策图(OBDD)被广泛用到网络可靠度的计算中,在基于OBDD计算网络可靠度时,其计算时间主要取决于参与操作的OBDD的大小,而OBDD的大小严重依赖于OBDD的变量序。该文根据布尔函数的性质和OBDD原理提出一种优化计算网络可靠性的算法(BF-OBDD),提高计算网络可靠性的效率。实验结果表明改进的算法有较少的OBDD节点数量,在计算网络可靠性时,花费的时间较少。
计算机网络;可靠性;网络拓扑图;有序二元决策图;变量序;布尔函数
1 引言
随着网络的快速发展,网络的可靠性在网络分析和设计中越来越重要,成为定量计算和定性分析中非常重要的性能指标。复杂网络一旦出现故障就会导致灾难性的后果。在IEEE90标准中把网络可靠性定义为“网络在规定时间和规定条件下完成它所需要完成功能的能力”。本文基于有序二元决策图(Ordered Binary Decision Diagram, OBDD)算法对网络连通可靠性进行了分析。
目前国内外学者对网络可靠性计算进行了大量的研究,主要分为两种类型,第1种是枚举最小路径集或最小割集[1]。最小路径集是包含所有最小路径的集合。当最小路径集中至少有一条最小路径是正常工作的,则表示网络是正常工作的。将网络可靠度表示为全部最小路径集的并,然后采用容斥原理法或不交化算法对其进行处理。这种方法在计算复杂网络的可靠度时,效率很低。第2种是基于网络拓扑图[2],通过对网络拓扑图中的边进行逐一分析,当边正常工作时,则压缩与该边相连的两端为一个节点,当边故障时,则删除该边。以此原则来分析网络的可靠性。当网络复杂,该算法需要分析很多条边,计算效率低。
自文献[3]于1978年提出全新的数据结构二元决策图(Binary Decision Diagram, BDD)以来,BDD被广泛用于网络可靠度的计算中[4]。基于BDD计算网络可靠度的算法具有节省数据结构空间和时间计算效率高的优点。在基于OBDD计算网络可靠度时,其计算时间主要取决于参与操作的OBDD的大小,而OBDD的大小严重依赖于OBDD的变量序[5]。文献[6]提出基于网络拓扑图得到变量序来计算网络可靠性。本文根据网络拓扑图和布尔函数的性质提出一种优化的基于网络拓扑图的变量排序算法(Boolean Function-OBDD, BF-OBDD),并与文献[6]提出的算法和基于网络拓扑图的深度优先算法进行比较,结果表明本算法产生的节点数较少,花费的时间较低。
2 OBDD原理
2.1 BDD
BDD是布尔函数的图形表示形式,BDD采用二叉树形式表示一个布尔函数。
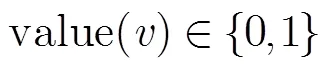

由上述定义1可看出,BDD是一个有根节点的有序二叉树,每个分支代表节点变量的一次取值(左支取1,右支取0)。从根节点出发到叶结点的每条路径都表示布尔函数中各变量的一次赋值。
2.2 OBDD

在有序二元决策图(OBDD)中,若节点满足以下两种性质,则称节点是相等的[9]:
(1)两个叶节点的值对应相等。
对于满足上述条件的OBDD节点,可以应用如下简化规则,有效地简化OBDD结构[10]:
(1)将叶节点为1的节点合并成一个节点,将叶节点为0的节点合并成一个节点。
3 最小路径集及布尔函数性质
3.1 最小路径集基本原理
网络是由一些节点以及连接某些节点对之间的边组成的一个图形。从指定的节点,经过一边序列(或其中的一部分边)可以到达节点,则称这个边序列为从到的一条路径。从节点到节点的边序列称为一条最小路径,则满足:(1)它是一条路径;(2)最小性。即从这个边序列中除去任意一条边后它即不是从到的路径,最小路径中包含的边数称为它的长度[11]。
3.2 布尔函数性质
4 基于OBDD计算网络可靠性算法
4.1 基于网络拓扑图得到OBDD变量序
由第3.2小节提到布尔函数吸收律的性质,本文提出基于网络拓扑图得到OBDD变量序的算法,算法步骤如下:
步骤1 从网络拓扑图中找出从源点到目的节点的最长最小路径,并将其边依次排在变量排序的最后;
步骤2 从网络拓扑图中找出从源点到目的节点的最短最小路径,将最短最小路径中未出现在变量排序中的边依次排在变量排序的最前面;
步骤3 继续搜索网络拓扑图中的最短最小路径,将该最小路径中未出现在变量序的边排在已存变量序之后。若无最短最小路径则转到步骤4;
步骤4 从网络拓扑图中找出从源点到目的节点的次短最小路径,将最短最小路径中未出现在变量排序中的边,放在已存变量序的后面;
步骤5 继续搜索网络拓扑图中的次短最小路径,将该最小路径中未出现在变量序的边排在已存变量序之后。若无次短最小路径则转到步骤6;
步骤6 按照最小路径的长度从短到长对最小路径依次进行选择,直到网络中所有的边都放进变量序中。
其中若有相同长度的最小路径,则根据最小路径中边的排序依次比较边的编号,先选择边的编号大的最小路径。
4.2 计算网络可靠性的步骤

步骤2 由网络拓扑图,结合本文提出的算法得到OBDD变量序;
步骤3 依据得到的OBDD变量序将逻辑结构函数用OBDD表示,本文在仿真中用哈希表来存储OBDD节点[13]。用哈希表来存储OBDD节点能保证生成的BDD节点是唯一的,并且能提高查找速度;
步骤4 从OBDD的根节点搜索到叶节点1的路径,可得到逻辑结构函数的不交化结果;
5 算法示例和仿真
以图1所示的网络拓扑图为例进行说明,其中节点1为源节点,节点6为目的节点。
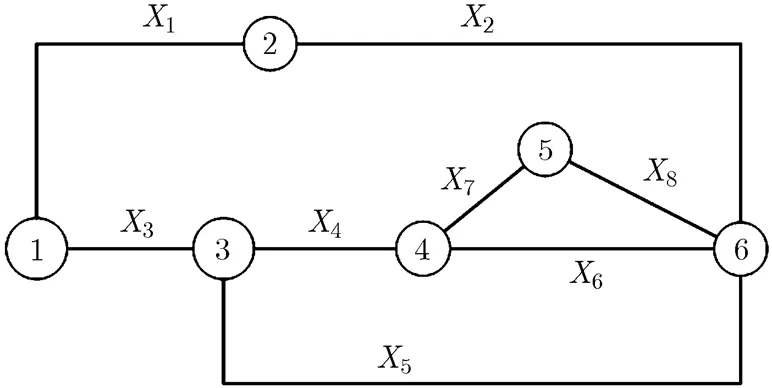
图1 网络拓扑图
5.1 OBDD变量序
5.2 计算网络可靠性

(2)按照OBDD的变量序对逻辑结构函数进行不交化处理得到OBDD,如图2所示。
图2 OBDD图形
(3)在OBDD图中搜索从根节点到叶节点1的路径,得到不交化的逻辑结构函数为

(4)网络可靠性计算符号表达式为
5.3 仿真


图3 实验网络
实验结果分别用图4、图5和图6表示,横坐标表示的是对应的网络拓扑图,纵坐标数值用指数形式表示。其中排序2和排序3为文献[6]提出的OBDD变量排序算法2和算法3。其中图4记录的是OBDD的节点数量,如在分析第8个网络可靠性时,基于本算法得到的OBDD节点数量为1795个,其它3种算法得到的节点数分别为2959个、3063个和9084个;图5记录的是创建OBDD图形所花费的时间;图6表示的是计算网络可靠性所花费的时间,当计算第8个网络可靠性时,BF-OBDD所花费的时间为16.5 s,其余3种算法所花费的时间分别为30.2 s, 233.0 s和25.2 s。根据图4可知,基于BF-OBDD算法计算网络可靠性时可以产生较少的OBDD节点数量。根据图5可知根据BF-OBDD算法在创建OBDD图形时花费的时间较少,由图6可以得到BF-OBDD算法在进行网络可靠性计算时,花费的时间较少。
6 结束语
在基于OBDD计算网络可靠性时,其计算时间主要取决于参与操作的OBDD的大小,而OBDD的大小严重依赖于OBDD的变量序。本文从网络拓扑图得到OBDD的变量序,由布尔函数的性质和OBDD原理提出了BF-OBDD算法,在计算网络可靠性时根据本算法能得到较少的OBDD节点数量,计算运行的时间较少。
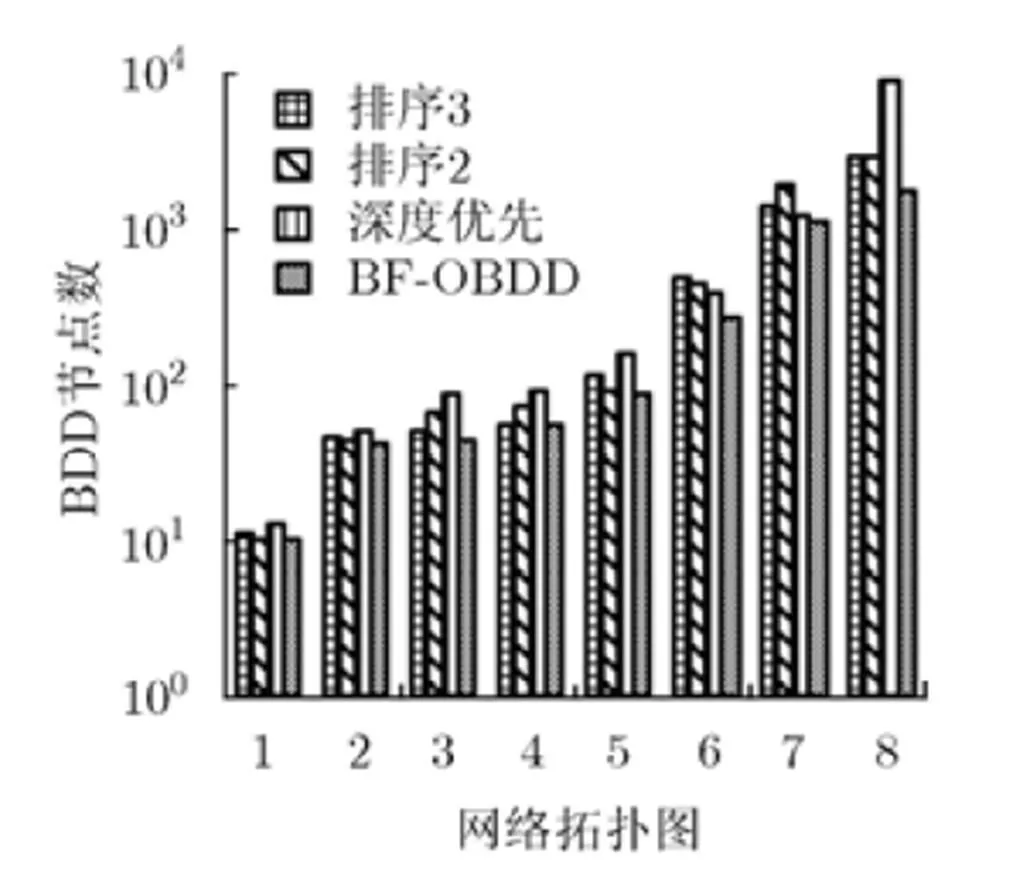
图4 OBDD节点数量

图5 OBDD节点创建时间
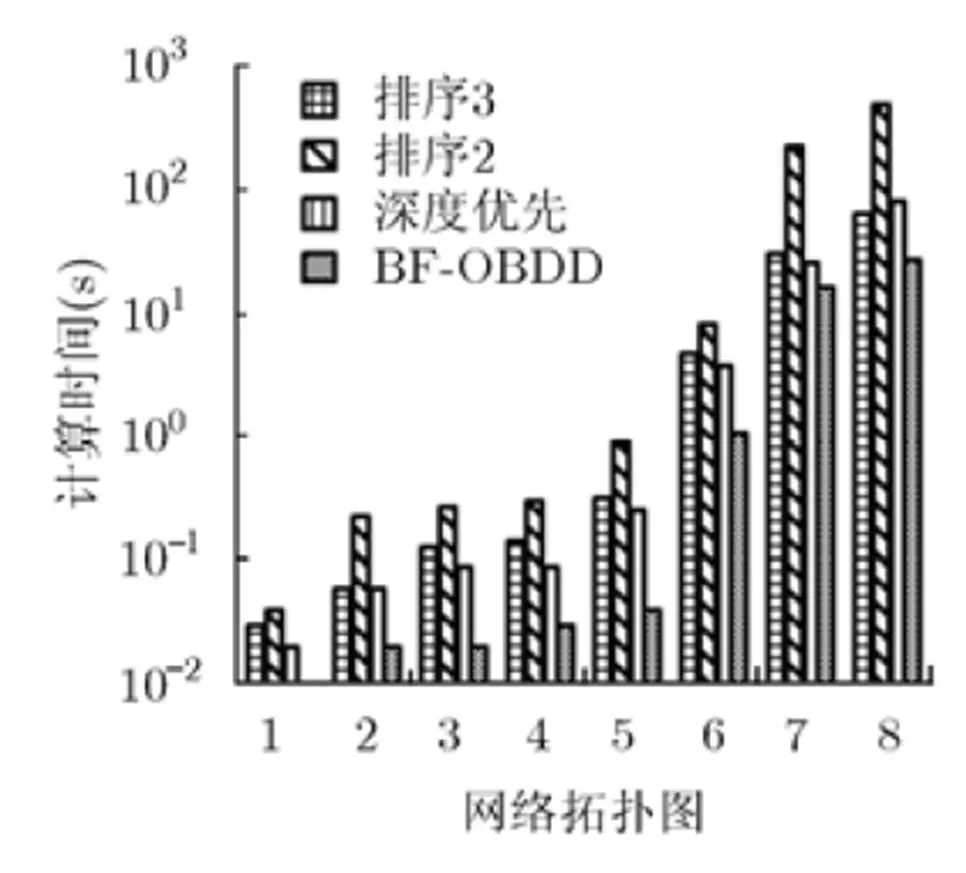
图6 可靠性计算时间
[1] 史玉芳, 陆宁, 李慧民. 基于改进的不交化最小路集的网络系统可靠性算法[J]. 计算机工程与科学, 2011, 33(1): 31-35.
Shi Yu-fang, Lu Ning, and Li Hui-min. An algorithm of network system reliability based on an improved disjointed minimal path set[J]., 2011, 33(1): 31-35.
[2] Wood R. Factoring algorithm for computing k-terminal network reliability[J]., 1986, 35(3): 269-278.
[3] Akers S. Binary decision diagrams[J]., 1978, 27(6): 509-516.
[4] LüGuan-feng, Chen Yao, Feng Ya-chao,A succinct and efficient implementation of 232bdd package[C]. IEEE Sixth International Symposium on Theoretical Aspects of Software Engineering, Beijing, China, 2012: 241-244.
[5] 陈瑶, 李峭, 赵长啸, 等. 基于OBDD的航空电子网络可靠性分析[J]. 系统工程与电子技术, 2013, 35(1): 230-236.
Chen Yao, Li Qiao, Zhao Chang-xiao,OBDD-based reliability analysis for avionics networks[J]., 2013, 35(1): 230-236.
[6] Zang X, Sun H, and Trivedi K. A bdd-based algorithm for reliability graph analysis[OL]. http://www.ee.duke.edu/~ hairong/workinduke/relgrap. 2000.
[7] Tatsuhiro Tsuchiya. A bdd-based approach to reliability optimal module allocation in networks[C]. IEEE 18th Pacific Rim International Symposium on Dependable Computing, Niigata, Japan, 2012: 121-126.
[8] Zhao Bo, Liu Yan, and Xiao Yu-feng. OBDD-based algorithm for reliability evaluation of wireless sensor networks[C]. Prognostics and Systems Health Management Conference, Beijing, China, 2012: 1-4.
[9] Friedman S and Supowit K. Finding the optimal variable ordering for binary decision diagrams[J]., 1990, 39(5): 710-713.
[10] Mahdi I and Nadji B. Application of the binary decision diagram(BDD) in the analysis of the reliability of the inverters[C]. Proceedings of 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 2013: 1265-1271.
[11] 曹晋华, 程侃. 可靠性数学引论[M]. 北京: 科学出版社, 1986: 89-90.
Cao Jin-hua and Cheng Kan. Reliability Mathematics Introduction[M]. Beijing: Science Press, 1986: 86-90.
[12] 古天龙, 徐周波. 有序二叉决策图及应用[M]. 北京: 科学出版社, 2009: 18-19.
Gu Tian-long and Xu Zhou-bo. Ordered Binary Decision Diagram and Its Application[M]. Beijing: Science Press, 2009: 18-19.
[13] Brance K, Rudell R, and Bryant R. Efficient implementation of a bdd package[C]. Proceedings of 27th ACM/IEEE DAC, New York, USA, 1990: 40-45.
[14] 赵勃, 肖宇峰, 刘岩. 基于OBDD的通信网链路重要性评估[J]. 系统工程与电子技术, 2011, 33(10): 2348-2352.
Zhao Bo, Xiao Yu-feng, and Liu Yan. Importance evaluation of communication network links based on OBDD[J]., 2011, 33(10): 2348-2352.
[15] Xing L. An efficient binary-decision-diagram -based approach for network reliability and sensitivity analysis[J].,,--:, 2008, 38(6): 105-115.
[16] Xiao Y, Lin X, Li Y,Evaluate reliability of wireless sensor network with obdd[C]. Proceedings of IEEE International Conference on Communications, Dresden, 2008: 105-115.
熊 飞: 男,1983年生,博士,工程师,研究方向为移动通信技术、通信网链路可靠性研究.
乔 迪: 男,1990年生,硕士,研究方向为网络可靠性研究.
王宏祥: 男,1973年生,博士,副教授,研究方向为网络可靠性研究.
赵子岩: 男,1975年生,博士,高级工程师,研究方向为网络流量、通信网络关键技术研究.
杨 洪: 男,1959年生,教授级高级工程师,研究方向为应急通信、软交换、网络安全研究.
沈 亮: 男,1969年生,教授级高级工程师,研究方向为信息通信网络架构和安全运维研究.
A Novel Network Reliability Evaluating Algorithm with Ordered Binary Decision Diagram Based on Boolean Function
Xiong Fei①Qiao Di②Wang Hong-xiang②Zhao Zi-yan①Yang Hong①Shen Liang①
①(&.,,100761,)②(,,100876,)
Ordered Binary Decision Diagram (OBDD) is commonly used in network reliability calculation. When evaluating the network reliability based on OBDD, computation time mainly depends on the size of the operating OBDD, which mostly relies on the variable ordering of OBDD. An algorithm is called BF-OBDD which is considered as the Boolean Function-OBDD, and it is the optimization algorithm for computing the reliability of the network. This paper shows that the reliability of network can be improved considerably by using of the proposed BF-OBDD algorithm. The experimental results demonstrate that the improved algorithm has less OBDD node numbers which cost less time when calculating the network reliability.
Computer networks; Reliability; Network topology; Ordered Binary Decision Diagram (OBDD); Variable order; Boolean function
TN915
A
1009-5896(2014)11-2786-05
10.3724/SP.J.1146.2014.00176
熊飞 xiongfei@sgcc.com.cn
2014-01-26收到,2014-05-15改回
国家863计划项目(2012AA011302),国家科技重大专项(2012ZX 03003007)和国家电网公司科技项目(SGIT2012335)资助课题
