基于线性混合模型的高光谱图像谱间压缩感知重构
2014-06-02王忠良贾应彪
王忠良 冯 燕 贾应彪
基于线性混合模型的高光谱图像谱间压缩感知重构
王忠良①②冯 燕*①贾应彪①
①(西北工业大学电子信息学院 西安 710129)②(铜陵学院电气工程系 铜陵 241000)
该文针对高光谱数据的线性混合模型,提出一种简单有效的谱间压缩感知下高光谱数据的重构方案。该方案不同于传统的压缩感知重构方法直接重构高光谱数据,而是将高光谱数据分离成端元和丰度分别进行重构,然后利用重构的端元和丰度信息合成高光谱数据。实验结果表明,该方案的重构质量明显优于标准压缩感知重构方法,并且运算速度具有极大提升,同时便于获得端元和丰度信息。
高光谱图像;压缩感知;感知矩阵;线性混合模型
1 引言
随着成像光谱技术的不断发展,高光谱遥感由于具有极强的地物分类和识别能力,已经成为遥感领域一个快速发展的重要分支。高光谱遥感技术可以同时提供空间域信息和光谱域信息,与单波段图像和彩色图像相比,高光谱图像提供了关于地物更细致的光谱信息。与传统遥感相比,随着光谱分辨率的不断提高,高光谱遥感所获取的数据量呈指数量级增加,给数据的计算、存储和传输都带来了巨大的压力。因此,有效地进行数据压缩是目前高光谱技术中迫切需要解决的难题。
压缩感知(Compressive Sengsing, CS)理论[1,2]提供了一种全新的信号采集框架,突破了传统的香农采样定理,将压缩和采样过程巧妙地结合起来,实现采样率低于传统奈奎斯特率下的数据采集。该信号采集方式具有编码简单、解码较复杂、能够实现较为高效的压缩、抗误码性能好等特点,这些特点非常适合机载或星载的高光谱遥感成像技术。
压缩感知数据的信号重构需要从较少的观测数据中精确恢复出原数据,因此重构时需要解决欠定方程的求解问题,可通过求解优化问题来实现。通过对CS理论的研究,产生了一系列重构算法,如BP(Basis Pursuit)[1],1-magic[3], C-SALSA(ConstrainedSplit Augmented Lagrangian Shrinkage Algorithm)[4], FISTA(Fast Iterative Shrinkage-Threshold Algorithm)[5]等。对于高光谱数据,文献[6]在分析高光谱图像压缩采样数据特性的基础上,提出了一种基于谱间预测和联合优化的压缩感知图像重构算法;文献[7]针对3维数据的特点,提出了3维CS和重构算法。文献[8]根据高光谱数据的稀疏性、空间相关性和谱间相关性,提出了一种基于复合正则化的高光谱图像压缩感知投影与重构方法。文献[9]根据高光谱图像具有较强的谱间相关性,提出了一种基于谱间线性滤波的高光谱图像压缩感知方法。所有这些算法都是直接重构原始数据,数据量大,处理速度慢。高光谱数据的线性混合模型(LMM)是对真实世界中的光谱混合模型的简化,作为一种常规而有效的光谱混合模型,被广泛应用于高光谱的混合像元分解[10]。该模型假设混合像元中不同端元间的多重散射可以忽略不记,任一像元矢量可表示成端元以及与该端元相应的丰度的线性组合,也就是说高光谱数据可以看做端元矩阵和丰度矩阵的乘积。
本文根据推扫式(pushbroom)和扫描式(whiskbrook)成像光谱仪的特点,在信号采集端采用谱间压缩采样,采样方式简单,易于机载或星载的高光谱压缩采样成像。在解码端根据高光谱数据的线性混合模型特点,将高光谱数据分离成端元和丰度分别进行重构,然后利用重构的端元和丰度信息合成高光谱数据。首先,该方案可以获得端元和丰度信息,省去了后续的解混运算,为CS理论在高光谱成像及后续分析处理中的应用提供了可实现方案。其次,所提方案不仅可以极大地提高图像的重构质量,而且由于重构的端元和丰度数据远小于原始高光谱数据,运算速度有了数量级的提升。
2 线性混合模型下的压缩感知重构方案
2.1 线性混合模型



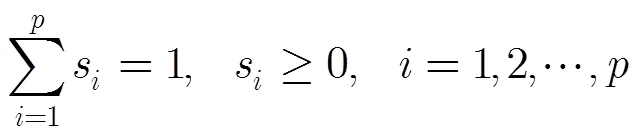
2.2高光谱压缩感知

高光谱图像由于具有丰富的细节信息,各波段的图像平滑性较差,其稀疏性稍差于普通图像,然而其谱间信息对应于端元特征信号的线性组合,往往具有很好的平滑性,即在小波等正交基下具有很好的稀疏性。针对此,本文在高光谱数据矩阵压缩度量时采用谱间压缩度量,该度量方式符合推扫式和扫描式成像光谱仪的成像特点,具体形式为下:
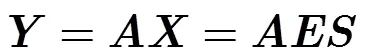
2.3重构方案
标准压缩感知重构时,通过求解式(5)的优化问题,从随机投影中重构原图像:
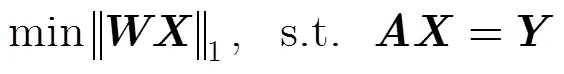

3 重构方案的实现
3.1 未知端元特征的重构(ULMMCR)




(2)将降维后的数据投影到超平面上,形成单形体;
(3)任意指定一初始方向,将超平面上的数据投影到该初始方向;
(6)再将超平面上的数据投影到新方向,投影极值对应的是下一端元向量,记下位置,返回5,直到找出所有端元;



算法:未知端元谱下,基于线性混合模型的高光谱压缩感知重构算法(ULMMCR):


3.2 已知端元特征的重构(LMMCR)

即通过式(12)和式(11)就可以实现压缩重构,此时的计算都是一次性完成的矩阵运算操作。

4 实验分析

4.1合成数据实验


图1 USGS矿物谱库中的4种端元谱

表1不同采样率下合成数据的重构结果

采样率MR平均PSNR(dB)运行时间(s) 标准CSULMMCRLMMCR标准CSULMMCRLMMCR 0.122.2123.49286.278942.060.014 0.223.7624.54287.363272.110.017 0.328.9429.38289.813842.030.015 0.429.2230.55287.273422.210.014 0.532.7833.90290.213142.230.016 18.5014.62267.3417441.090.013
4.2 真实数据实验



图2 采样率为0.2、端元数为4时,Cuprite第30波段的原始图像与重建图像
表2不同采样率下真实数据的重构结果

采样率MR平均PSNR(dB)运行时间(s) 标准CSULMMCRLMMCR标准CS(×103)ULMMCRLMMCR 0.118.7731.3843.9614.242.650.12 0.224.4032.9344.5310.702.530.11 0.330.8733.1244.6914.552.180.13 0.434.2636.6544.918.872.690.13 0.536.5638.8044.878.612.610.13 12.7813.9743.2625.281.580.11
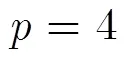
5 结束语
本文提出了一种简单而有效的高光谱压缩感知重构方案,该方案依赖于两点假设:所采用的压缩感知方式为谱间压缩采样;高光谱数据满足线性混合模型。所提方案不同于传统的高光谱CS直接重构原始数据,而是分别对端元和丰度数据进行重构,再合成原始数据,将海量的高光谱数据分解成两个子数据进行处理,极大地减少了处理时间,提高了运行速度。文中分别讨论了端元特征谱已知和未知两种情况下,压缩数据重构的策略。仿真和真实数据实验表明,所提方案在极大减少处理时间的同时,重构性能还有明显改善,特别是在已知端元特征情况下,性能改善更明显。同时该方法还提供了端元和丰度信息的估计,省去了对压缩感知重构数据的解混运算。
本方案是针对谱间压缩的高光谱数据重构,在将来的研究工作中,要考虑空间压缩情况下,基于线性混合模型的高光谱CS重构;同时,本文没有对压缩感知下端元提取和端元重构更有效的算法进行研究,这是我们在将来的研究工作中需要解决的问题之一。
[1] Donoho D L. Compressed sensing[J].,2006, 52(4): 1289-1306.
[2] Candes E J and Wakin M B. An introduction to compressive sampling[J].,2008, 25(2): 21-30.
[3] Candes E J and Romberg JK. The1-magic toolbox[OL]. http://www.l1-magic.org, 2008.
[4] Afonso M V,Bioucas-DiasJM, and FigueiredoM A T.An augmented lagrangian approach to the constrained optimization formulation of imaging inverse problems[J].,2011,20(3): 681-695.
[5] Shia VYang A Y, Sastry SS,. Fast1minimization and parallelization for face recognition[C]. Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), PacificGrove, 2011: 1199-1203.
[6] 刘海英, 吴成柯, 吕沛, 等. 基于谱间预测和联合优化的高光谱压缩感知图像重构[J]. 电子与信息学报, 2011, 33(9): 2248-2252.
Liu Hai-ying, Wu Cheng-ke, Lü Pei,.Compressed hyperspectral image sensing reconstructionbased on interband prediction and joint optimization[J].&,2011, 33(9): 2248-2252.
[7] Shu Xian-biao and Ahuja N. Imaging via three-dimensional compressive sampling (3DCS)[C]. IEEE International Conference on Computer Vision (ICCV), Barcelona, 2011: 439-446.
[8] 冯燕, 贾应彪, 曹宇明, 等. 高光谱图像压缩感知投影与复合正则重构[J]. 航空学报, 2012, 33(8): 1466-1473.
Feng Yan, Jia Ying-biao, Cao Yu-ming,.Compressed sensing projection and compound regularizer reconstruction for hyperspectral images[J]., 2012, 33(8): 1466-1473.
[9] 计振兴, 孔繁锵. 基于谱间线性滤波的高光谱图像压缩感知[J]. 光子学报, 2012, 41(1): 82-86.
Ji Zhen-xing and Kong Fan-qiang. Hyperspectral image compressed sensing based on linear fillter between bands[J]., 2012, 41(1): 82-86.
[10] Bioucas-Dias JMPlazaA, DobigeonN,. Hyperspectral unmixing overview: geometrical, statistical, and sparse regression-based approaches[J]., 2012, 5(2): 354-379.
[11] Wang Zhong-liangFengYan, and Jia Yin-biao.Spatial-spectral compressive sensing of hyperspectral image[C]. Third IEEE International Conference on Information Science and Technology, Yangzhou, 2013: 1256-1259.
[12] Ly NHDu Qian, and Fowler J E.Reconstruction from random projections of hyperspectral imagery with spectral and spatial partitioning[J].,2013, 6(2): 466-472.
[13] Li Cheng-boSunTing, KellyKF,. A compressive sensing and unmixing scheme for hyperspectral data processing[J]., 2012, 21(2): 1200-1210.
[14] Nascimento J M P and Dias J M B. Vertex component analysis: a fast algorithm to unmix hyperspectral data[J]., 2005,43(4): 898-910.
[15] Heylen R,Burazerovic D, and ScheundersP. Fully constrained least squares spectral unmixing by simplex projection[J].,2011, 49(11): 4112-4122.
[16] PuHan-yeXiaWei, WangBin,.A fully constrained linear spectral unmixing algorithm based on distance geometry[J]., 201452(2): 1157-1176.
[17] 焦李成, 杨淑媛, 刘芳, 等. 图像压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651-1662.
Jiao Li-cheng, Yang Shu-yuan, Liu Fang,. Development and prospect of compressive sensing [J].,2011, 39(7): 1651-1662.
[18] VaneG, Green R O, ChrienTG,. The airborne visible infrared imaging spectrometer (aviris)[J]., 1993, 44(2): 127-143.
王忠良: 男,1980年生,博士生,讲师,研究方向为高光谱图像压缩感知和解混、图像处理.
冯 燕: 女,1963年生,教授,研究方向为高光谱图像压缩和分类、图像处理和智能信息处理等.
贾应彪: 男,1977年生,博士生,讲师,研究方向为压缩感知理论与数字图像处理技术.
1)http://speclab.cr.usgs.gov/spectral-lib.html
Reconstruction of Hyperspectral Images with Spectral Compressive Sensing Based on Linear Mixing Models
Wang Zhong-liang①②Feng Yan①Jia Ying-biao①
①(,,’710129,)Department of Electric EngineeringTongling UniversityTonglingChina
A simple and effective reconstruction scheme of hyperspectral data with spectral Compressive Sensing (CS) is proposed based on the widely used linear mixing model. The scheme is different from the traditional reconstruction methods of compressive sensing, which reconstruct hyperspectral data directly. The proposed scheme separates hyperspectral data into endmembers and abundances to reconstruct respectively, then generates hyperspectral data by reconstructed endmembers and abundances. Experimental results show that the reconstruction quality of the proposed scheme is better than the standard compressive sensing, furthermore the computing speed greatly ascends. Simultaneously, as a byproduct, endmembers and abundances can be obtained directly.
Hyperspectral images; Compressive Sensing (CS); Sensing matrix; Linear mixing models
TP751.2
A
1009-5896(2014)11-2737-07
10.3724/SP.J.1146.2013.01511
冯燕 sycfy@nwpu.edu.cn
2013-09-30收到,2014-08-11改回
国家自然科学基金(61071171)和安徽省高等学校省级自然科学研究项目(KJ2013B298)资助课题
