基于主成分分析和字典学习的高光谱遥感图像去噪方法

2014-06-02霍雷刚冯象初

电子与信息学报 2014年11期

霍雷刚冯象初

霍雷刚*冯象初

(西安电子科技大学数学与统计学院西安 710126)

高光谱图像变换域各波段图像噪声强度不同，并具有独特的结构。针对这些特点，该文提出一种基于主成分分析(Principal Component Analysis, PCA)和字典学习的高光谱遥感图像去噪新方法。首先，对高光谱数据进行PCA变换得到一组主成分图像；然后，对信息量较小的主成分图像分别采用基于自适应字典的稀疏表示方法和对偶树复小波变换方法去除空间维和光谱维的噪声；最后，通过PCA逆变换得出去噪后的数据。结合主成分分析和字典学习的优势，该文方法相对于传统方法对高光谱图像具有更好的自适应性，在细节得到保留的同时有效地抑制了斑块效应。对模拟和实际高光谱遥感图像的实验结果验证了该文方法的有效性。

图像处理；高光谱图像；去噪；主成分分析；稀疏表示；字典学习

1 引言

近年来，高光谱遥感图像受到广泛关注，并成功应用到地质勘探、考古发现、森林火灾检测、军事作战等多个领域。然而，由于在获取、传输过程中受到各种因素的影响，高光谱遥感图像的噪声比较严重。这些噪声对后续的解混[1]、分类[2]和识别[3]等造成严重影响，制约了高光谱图像的广泛应用。因此，图像去噪技术是高光谱遥感应用中非常重要的关键技术之一，也是遥感科学和信息科学的研究热点。

与全色图像、多光谱图像相比，高光谱图像的噪声更加复杂。一方面，高光谱图像的波段数较多，各波段图像受噪声影响的程度不同；另一方面，由于光谱分辨率较高(单个波段的光谱频率范围较窄)，各波段之间的相关性较强。上述特点使得传统的全色图像、彩色图像和多光谱图像去噪方法不能很好地用于去除高光谱图像中的噪声。因此，有必要针对高光谱图像的特点，设计更加合理的去噪方法。根据是否对高光谱数据进行光谱维变换，传统的高光谱图像去噪方法基本上可以分为两大类：(1)直接对获取的高光谱数据在空间维和光谱维建立去噪模型。例如：文献[4]把高光谱图像看作超立方体，研究了基于3维各向异性扩散的高光谱图像增强方法；文献[5]提出光谱-空间维自适应的总变差模型；文献[6]在最大后验估计框架下提出空间-光谱维混合先验模型等；(2)先将高光谱数据进行光谱维变换，在变换后的空间维和光谱维进行去噪，然后进行逆变换得到去噪后的数据。例如：文献[7]提出在光谱微分域采用小波阈值收缩方法去噪；文献[8]提出在光谱微分域采用BayesShrink算法和Savitzky- Golay滤波进行去噪；文献[9]提出一种基于主成分分析和小波阈值收缩的高光谱图像去噪方法等。

以上方法考虑了高光谱图像的特点，但没有充分利用高光谱数据本身的特性。例如，文献[9]对主成分图像采用对偶树复小波变换，这些事先定义的、固定的解析字典没有充分考虑数据本身的属性，使得去噪方法对每个主成分图像去噪的自适应性受到限制。

针对上述缺陷，本文提出一种基于主成分分析和字典学习的高光谱图像去噪新方法。一方面，新方法充分利用PCA变换的优点，前几个主成分图像携带的主要信息得以有效保留；另一方面，新方法根据当前数据自适应地学习字典，结合稀疏表示方法对每个噪声成分图像进行去噪。由于字典是自适应学习的，更加全面地反映了数据的特殊性。

本文的结构安排为：第2节详细叙述了本文提出的方法；第3节是对实验结果的分析；结论在第4节给出。

2 基于主成分分析和字典学习的高光谱图像去噪方法

如前所述，本文方法的基本原理是综合利用光谱维变换和字典学习的优点来解决高光谱图像去噪的问题。不失一般性，本文结合经典的主成分分析[10]和基于K-奇异值分解(K-Singular Value Decomposition, K-SVD)算法[11]的图像去噪模型[12]给出一种新的高光谱图像去噪方法。

本文的方法主要包括如下4个步骤：

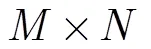
2.1 主成分分析

主成分分析[10]是一种最基本的数据降维方法，主要是通过对数据的协方差矩阵进行特征值分解，特征值分解后的特征向量对应数据的主成分，特征值对应数据在各个主成分上的权重。因此，PCA变换是一种线性变换，变换后各主成分分量彼此不相关，且随着主成分编号的增加该分量包含的信息量减小。同其他基于光谱维变换的高光谱图像去噪方法一样，本文的方法主要是利用PCA变换去除高光谱图像波段间的相关性，去除冗余信息。对高光谱图像进行PCA变换后，大部分信息集中在前几个主成分分量中，其他的主成分分量以噪声为主，本文称之为噪声成分分量。通常可以只取前几个信息量大的主成分分量而丢掉信息量小的噪声成分分量。值得注意的是，噪声成分分量仍包含一些有用信息，如果丢弃噪声成分分量，重构的高光谱图像将会有信息损失。针对以上情况，文献[9]提出保留信息量大的前几个主成分分量，对噪声成分分量进行去噪，然后取处理后的所有主成分分量进行PCA逆变换。本文也采用这种方式。

2.2 基于K-SVD模型的噪声成分图像去噪

小波变换由于具有良好的时频特性，在信号和图像处理领域应用广泛。传统的基于阈值收缩的小波去噪方法考虑了小波系数的大小但忽略了小波系数的结构信息，很多学者对其进行改进，如采用双变量收缩的方法[15]，结合稀疏表示的方法[16]等。根据信号的先验知识，可以设计出合适的字典。进一步，考虑信号样本，可以优化这些字典[17]。近年来，稀疏表示理论和字典学习算法的研究取得了很大的进展。字典学习的方法因其对不同图像的自适应性获得了比采用固定字典方法更好的效果，已被成功地用于图像去噪[12,18]、Bayer格式图像彩色恢复[19]、高光谱遥感图像分类[20]等。其中，K-SVD算法[11]是目前最具代表性的字典学习方法之一。

经过适当地初始化，上述优化问题中的待求变量可以采用交替迭代的方法按如下步骤求解[12]：

步骤1和步骤2交替迭代进行，直到满足停止条件(达到指定最大迭代次数或误差)。

3 实验结果

3.1 模拟数据实验结果

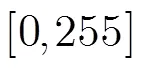
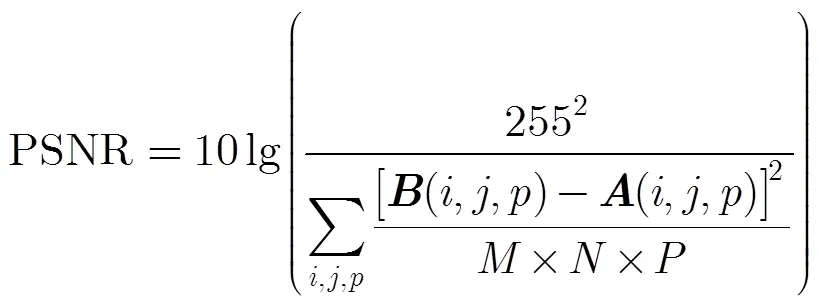
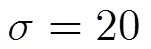
由于噪声强度随波长变化，为进一步比较不同方法在每个波段上的去噪性能，图2显示了第(2)种情况和第(3)种情况下(即噪声强度随波段变化的情况)每隔5个波段含噪声数据和不同去噪方法去噪后数据在各个波段上的信噪比之差(峰值信噪比之差的比较与此类似)，其他未显示的波段的比较结果与此类似。从中可以看出，BandBishr2D方法去噪的性能偏低，BandK-SVD2D 方法较BandBishr2D方法效果有所提升，部分波段达到甚至超过了4种方法在该波段达到的最高信噪比(例如第1个波段)。PCABishr2D 方法和本文方法在所有波段都取得了很好的去噪效果，整体比较稳定且大多数波段高于前两种方法。其中，本文方法去噪效果较PCABishr2D 方法又有所提升，并且对大部分波段提升效果明显。

表1模拟数据上4种方法去噪性能比较(所有波段的噪声强度都相同的情况)

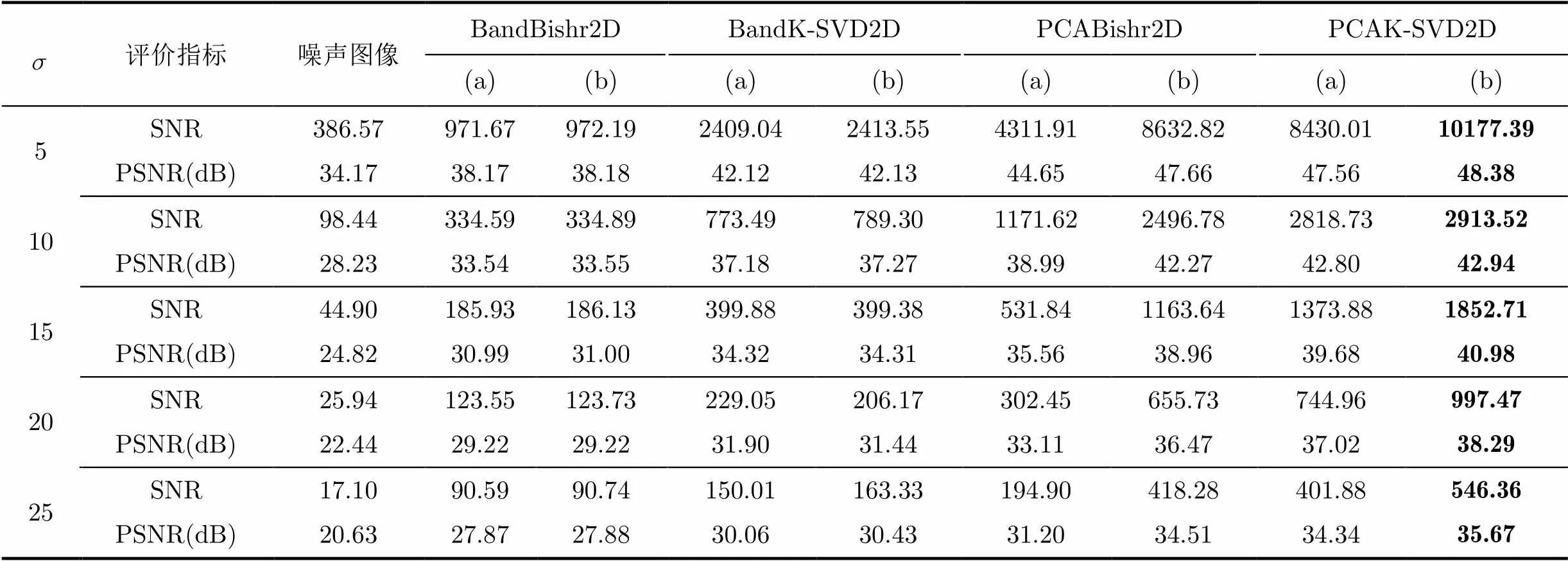
评价指标噪声图像BandBishr2DBandK-SVD2DPCABishr2DPCAK-SVD2D (a)(b)(a)(b)(a)(b)(a)(b) 5SNR386.57971.67972.192409.042413.554311.918632.828430.0110177.39 PSNR(dB)34.1738.1738.1842.1242.1344.6547.6647.5648.38 10SNR98.44334.59334.89773.49789.301171.622496.782818.732913.52 PSNR(dB)28.2333.5433.5537.1837.2738.9942.2742.8042.94 15SNR44.90185.93186.13399.88399.38531.841163.641373.881852.71 PSNR(dB)24.8230.9931.0034.3234.3135.5638.9639.6840.98 20SNR25.94123.55123.73229.05206.17302.45655.73744.96997.47 PSNR(dB)22.4429.2229.2231.9031.4433.1136.4737.0238.29 25SNR17.1090.5990.74150.01163.33194.90418.28401.88546.36 PSNR(dB)20.6327.8727.8830.0630.4331.2034.5134.3435.67

注：(a)列为光谱维不进行处理时的结果；(b)列为光谱维去噪后的结果。

表2模拟数据上4种方法的去噪性能比较(噪声强度随波段变化的情况)

评价指标噪声图像BandBishr2DBandK-SVD2DPCABishr2DPCAK-SVD2D (a)(b)(a)(b)(a)(b)(a)(b) SNR217.18643.52643.881576.891584.152474.084563.185912.816938.06 PSNR(dB)31.6436.3836.3940.2840.3042.2344.8946.0246.71 SNR361.69874.83875.482235.002202.483870.566720.268979.139776.35 PSNR(dB)33.8837.7237.7241.7941.7344.1846.5747.8348.20

图2 模拟数据上不同去噪方法去噪后数据和含噪声数据的信噪比差值比较

3.2 真实数据实验结果

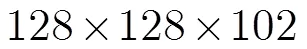
图3 真实数据上不同算法的去噪结果比较

表3真实数据和不同方法去噪后数据的MAQI指标

方法真实数据BandBishr2DBandK-SVD2DPCABishr2DPCAK-SVD2D MAQI0.01640.01670.01680.01660.0177

图4采用不同方法去噪后数据和真实数据各波段的AQI指标差值比较

4 结束语

高光谱图像变换域各波段噪声强度不同，为利用各波段图像的独特结构并提高去噪性能，本文提出了一种基于主成分分析和字典学习的高光谱遥感图像去噪新方法。该方法根据当前数据学习自适应字典，利用稀疏表示方法对噪声成分图像去噪。由于字典反应了图像本身的结构，本文方法在保留细节的同时有效抑制了斑块效应。该方法可以推广到采用其他光谱维变换和字典学习的方法，也可以将本文方法加以改进，针对非高斯噪声的情况设计合理的去噪模型或算法。

[1] Eches O, Benediktsson J A, Dobigeon N,Adaptive markov random fields for joint unmixing and segmentation of hyperspectral images[J]., 2013, 22(1): 5-16.

[2] Bai Jun, Xiang Shi-ming, and Pan Chun-hong. A graph-based classification method for hyperspectral images[J]., 2013, 51(2): 803-817.

[3] Li Qing-ting, Lu Lin-lin, Zhang Bing,The recognition of altered rock based on spectral modeling and matching using hyperspectral data[C]. Proceedings of 2nd IEEE International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, 2012: 1-4.

[4] Martín-Herrero J. Anisotropic diffusion in the hypercube[J]., 2007, 45(5): 1386-1398.

[5] Yuan Qiang-qiang, Zhang Liang-pei, and Shen Huan-feng. Hyperspectral image denoising employing a spectral-spatial adaptive total variation model[J]., 2012, 50(10): 3660-3677.

[6] Chen Shao-lin, Hu Xi-yuan, and Peng Si-long. Hyperspectral imagery denoising using a spatial-spectral domain mixing prior[J]., 2012, 27(4): 851-861.

[7] Othman H and Qian Shen-en. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative domain wavelet shrinkage[J]., 2006, 44(2): 397-408.

[8] 孙蕾, 罗建书. 高光谱遥感图像微分域三维混合去噪方法[J]. 光谱学与光谱分析, 2009, 29(10): 2717-2720.

Sun Lei and Luo Jian-shu. Three-dimensional hybrid denoising algorithm in derivative domain for hyperspectral remote sensing imagery[J]., 2009, 29(10): 2717-2720.

[9] Chen Guang-yi and Qian Shen-en. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage[J]., 2011, 49(3): 973-980.

[10] Jolliffe I T. Principal Component Analysis[M]. Second Edition, New York: Springer, 2002: 1-6.

[11] Aharon M, Elad M, and Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]., 2006, 54(11): 4311-4322.

[12] Elad M and Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]., 2006, 15(12): 3736-3745.

[13] Donoho D L and Johnstone I M. Ideal spatial adaptation by wavelet shrinkage[J]., 1994, 81(3): 425-455.

[14] Chen Guang-yi and Zhu Wei-ping. Signal denoising using neighbouring dual-tree complex wavelet coefficients[C]. Proceedings of 22nd Canadian Conference on Electrical and Computer Engineering, St Johns, NL, 2009: 565-568.

[15] Sendur L and Selesnick I W. Bivariate shrinkage with local variance estimation[J]., 2002, 9(12): 438-441.

[16] Zhao Rui-zhen, Liu Xiao-yu, Li Ching-chung,Wavelet denoising via sparse representation[J].:, 2009, 52(8): 1371-1377.

[17] Mallat S. A Wavelet Tour of Signal Processing: The Sparse Way[M]. Third Edition, San Diego: Academic Press, 2008: 693-695.

[18] Hao Yan, Feng Xiang-chu, and Xu Jian-lou. Multiplicative noise removal via sparse and redundant representations over learned dictionaries and total variation[J]., 2012, 92(6): 1536-1549.

[19] 朱波, 汶德胜, 王飞, 等. 应用字典学习算法改善Bayer格式图像彩色恢复效果[J]. 电子与信息学报, 2013, 35(4): 812-819.

Zhu Bo, Wen De-sheng, Wang Fei,Improvement of Bayer-pattern demosaicking with dictionary learning algorithm[J].&, 2013, 35(4): 812-819.

[20] 宋相法, 焦李成. 基于稀疏表示及光谱信息的高光谱遥感图像分类[J]. 电子与信息学报, 2013, 34(2): 268-272.

Song Xiang-fa and Jiao Li-cheng. Classification of hyperspectral remote sensing image based on sparse representation and spectral information[J].&2013, 34(2): 268-272.

[21] Pati Y C, Rezaiifar R, and Krishnaprasad P S. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition[C]. Proceedings of 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 1993: 40-44.

[22] Hyperspectral Remote Sensing Scenes[OL].http://www.ehu. es/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes, 2013. 10.

[23] Landgrebe D and Biehl L. MultiSpec[OL]. https:// engineering.purdue.edu/~biehl/MultiSpec/, 2013.10.

[24] Clark R N, Swayze G A, Wise R,USGS digital spectral library splib06a, 2007[OL]. http://speclab.cr.usgs.gov/ spectral.lib06/, 2013. 10.

[25] Qian Yun-tao and Ye Min-chao. Hyperspectral imagery restoration using nonlocal spectral-spatial structured sparse representation with noise estimation[J]., 2013, 6(2): 499-515.

[26] Gabarba S and Cristobal G. Blind image quality assessment through anisotropy[J].&, 2007, 24(12): 42-51.

霍雷刚：男，1986年生，博士生，研究方向为高光谱图像去噪模型和算法.

冯象初：男，1962年生，教授，研究方向为小波理论及应用、数值分析、图像处理等.

Denoising of Hyperspectral Remote Sensing Image Based on Principal Component Analysis and Dictionary Learning

Huo Lei-gang Feng Xiang-chu

(,,’710126,)

To reflect different intensities of noises among the different bands in the transform domain and the intrinsic structures of the transformed data, a new approach for denoising the hyperspectral images is proposed based on Principal Component Analysis (PCA) and dictionary learning. At first, a group of the principle component images are achieved by using the PCA transform. Then, these noises which exist in the spatial- and the spectral- domain of the components with low energy are denoised by an adaptively learned dictionary based sparse representation method and the dual-tree complex wavelet transform, respectively. Finally, the denoised data is obtained using the inverse PCA transform. By taking advantages of principal component analysis and dictionary learning, the proposed approach is superior to the traditional ones in preserving the details and alleviating the blocking artifacts. The experiment results on the synthetic and real hyperspectral remote sensing images demonstrate the effectiveness of the proposed approach.

Image processing; Hyperspectral image; Denoising; Principal Component Analysis (PCA); Sparse representation; Dictionary learning

TP751

1009-5896(2014)11-2723-07

10.3724/SP.J.1146.2013.01840

霍雷刚 leiganghuo@163.com

2013-11-22收到，2014-03-13改回

国家自然科学基金(61271294, 60872138)资助课题