基于椭球不确定集约束的鲁棒自适应相干检测器

代保全 王 彤 同亚龙 吴建新 保 铮



基于椭球不确定集约束的鲁棒自适应相干检测器

代保全 王 彤*同亚龙 吴建新 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对存在导向矢量误差时自适应相干检测器(ACE)的检测性能下降问题，该文提出一种基于椭球不确定集约束的鲁棒ACE设计方法。该方法在深入分析ACE检测器工作原理的基础上，利用导向矢量的尺度变化不影响ACE检测器输出这一特点，建立鲁棒ACE检测器模型并将其转化为凸优化问题，最后采用牛顿-拉夫森方法对该问题进行求解。仿真实验结果表明，该方法可有效提高ACE检测器对导向矢量误差的鲁棒性。

雷达信号处理；自适应相干检测器；导向矢量误差；椭球不确定集；鲁棒检测

1 引言

上述方法所建立的导向矢量模型与导向矢量的尺度有关，而ACE检测器与导向矢量的尺度无关，因此并不适用于改善ACE检测器对导向矢量误差的敏感性。针对这种情况，本文给出了一种鲁棒ACE检测器的设计方法。首先假设真实导向矢量位于一椭球不确定集[14]内，然后根据ACE检测器的特点，将鲁棒ACE设计问题转化为凸优化问题，最后采用牛顿-拉夫森方法求解该优化问题。本文方法适用于包括波束指向误差以及阵元幅相误差在内的多种导向矢量误差情况，仿真实验验证了该方法的有效性。

2 信号模型

经整理后，式(3)可以写成式(5)形式[1,2]：

实际上，式(3)也可以表示成式(6)形式：

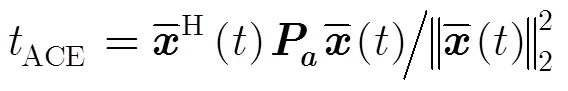
3 鲁棒ACE检测器算法原理

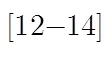
图1 ACE检测器示意图

3.1算法提出

则式(9)中的椭球不确定集约束可以转化为如式(11)的球不确定集约束。

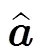
则式(11)可转化为式(12)：

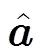
这里，我们采用Lagrange乘子算法[13,14]对式(16)进行求解。

对式(17)进行整理有

显然，如果满足

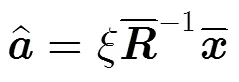
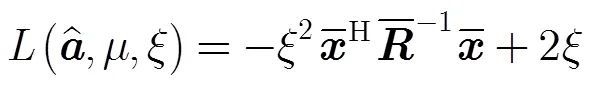
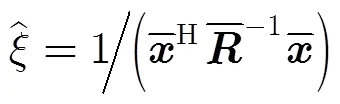
将式(21)代入式(20)有

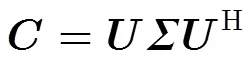
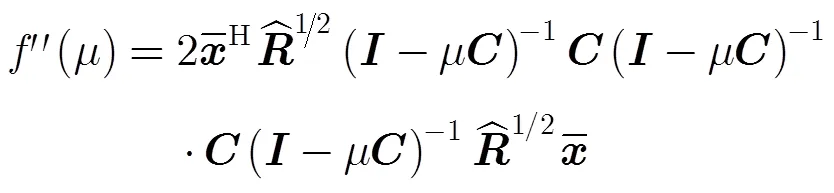
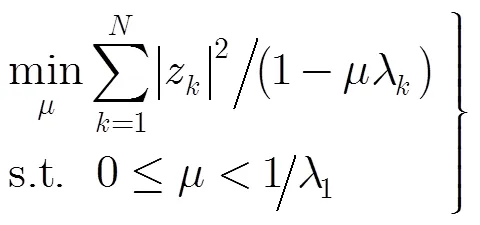
3.2算法实施步骤

本文算法的实施步骤总结如下：

步骤1 利用式(10)将椭球不确定集约束转化为球不确定集约束。

3.3运算量分析

4 仿真分析

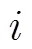
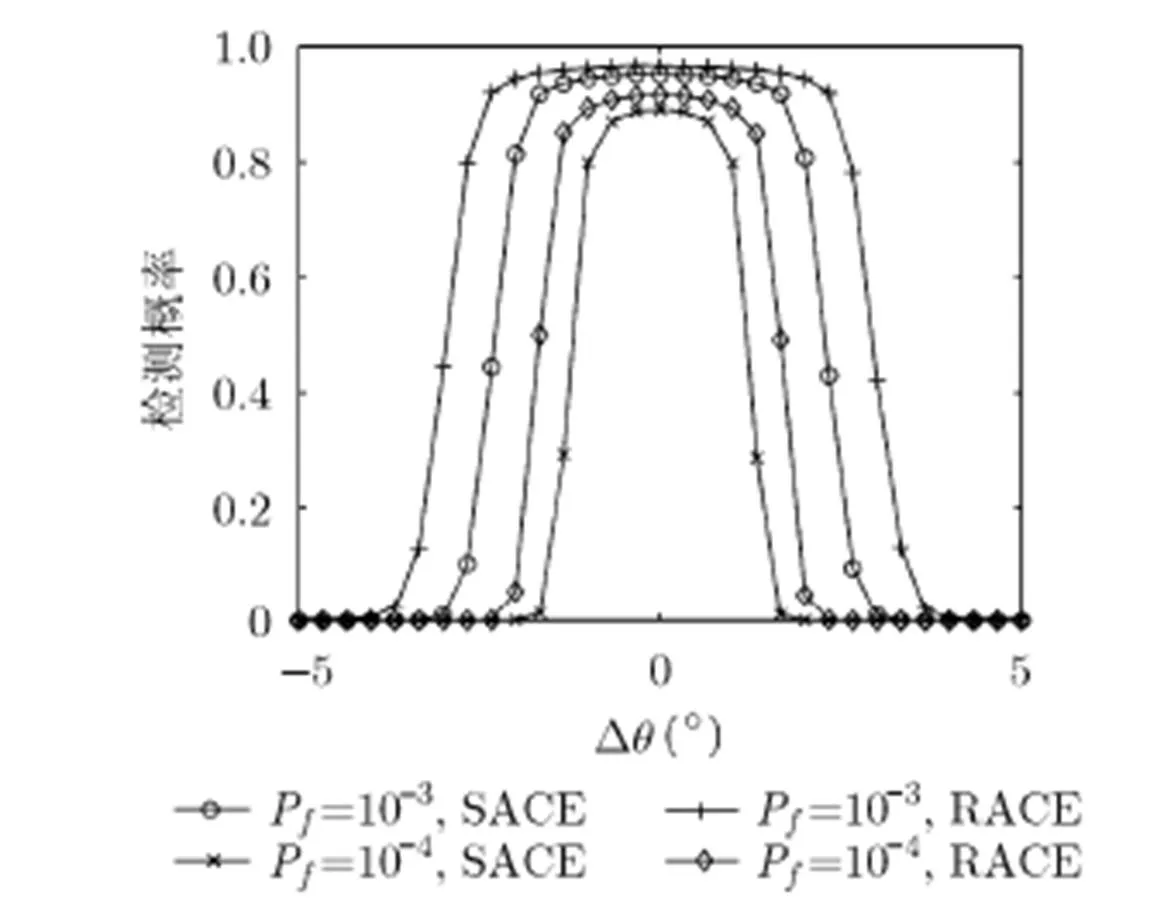
图3 检测概率随指向误差的变化情况

图4 存在幅相误差时，检测概率随指向误差的变化情况

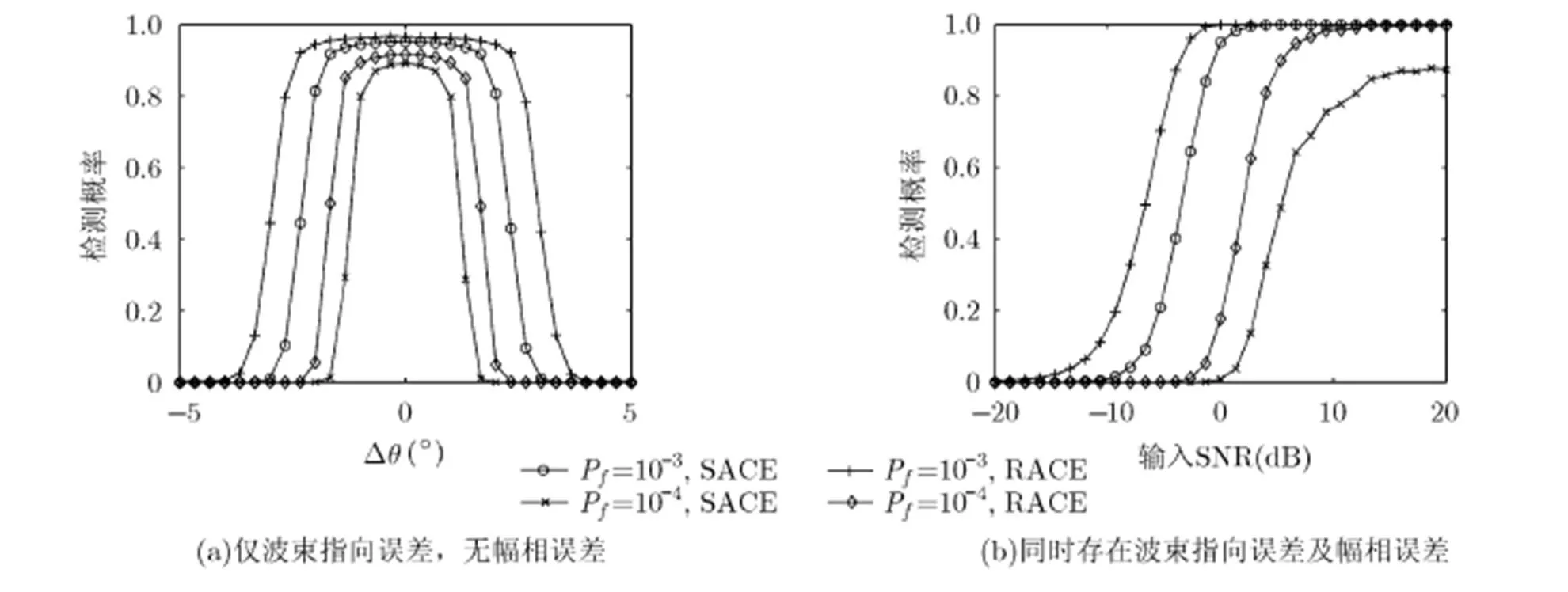
图5 检测概率随输入信噪比的变化情况

5 结束语

针对存在导向矢量误差时ACE检测器性能下降这一问题，在深入分析ACE检测器的工作机理及其影响参数的基础上，本文提出了一种基于椭球不确定集约束的鲁棒ACE检测器设计方法。利用导向矢量的尺度不影响输出ACE检测器输出这一特性，将非凸的鲁棒ACE检测器设计问题转化为凸优化问题，并给出了求解该问题的具体实施步骤。仿真结果表明，本文所给出的ACE检测器具有较好的导向矢量误差适应能力，能够在有效抑制旁瓣目标的同时，降低检测器对导向矢量误差的敏感性。需要说明的是本文方法在给定椭球不确定集的情况下，可以设计出具有较强鲁棒性的ACE检测器，但如何根据实际导向矢量误差情况构建适当的椭球不确定集这一问题并没有涉及，还需进一步研究。

[1] Kraut S, Scharf L, and Butler R. The adaptive coherence estimator: a uniformly most-powerful-invariant adaptive detection statistic[J]., 2005, 53(2): 427-438.

[2] Bidon S, Besson O, and Tourneret J. The adaptive coherence estimator is the generalized likelihood ratio test for a class of heterogeneous environments[J]., 2008, 15: 281-284.

[3] Wang P, Sahinoglu Z, Pun M,.. Knowledge-aided adaptive coherence estimator in stochastic partially homogeneous environments[J]., 2011, 18(3): 193-196.

[4] Raghavan R. Maximal invariants and performance of some invariant hypothesis tests for an adaptive detection problem[J]., 2013, 61(14): 3607-3619.

[5] Liu Jun, Zhang Zi-jing, Shui Peng-lang,.. Exact performance analysis of an adaptive subspace detector[J]., 2012, 60(9): 4945-4950.

[6] Hossain M, Milford G, Reed M,.. Efficient robust broadband antenna array processor in the presence of look direction errors[J]., 2013, 61(2): 718-727.

[7] De Maio A, De Nicola S, Farina A,.. Adaptive detection of a signal with angle uncertainty[J].&, 2010, 4(4): 537-547.

[8] Zhang Wei, Wang Ju, and Wu Si-liang. Robust Capon beamforming against large DOA mismatch[J]., 2013, 93(4): 804-810.

[9] Liu Ai-fei, Liao Gui-sheng, Ma Lun,.. An array error estimation method for constellation SAR systems[J]., 2010, 7(4): 731-735.

[10] Jia Wei-min, Jin Wei, Zhou Shu-hua,.. Robust adaptive beamforming based on a new steering vector estimation algorithm[J]., 2013, 93(9): 2539-2542.

[11] Khabbazibasmenj A, Vorobyov S A, and Hassanien A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]., 2012, 60(6): 2974-2987.

[12] 金伟, 贾维敏, 姚敏立. 迭代对角加载采样矩阵求逆鲁棒自适应波束形成[J]. 电子与信息学报, 2012, 34(5): 1120-1125.

Jin Wei, Jia Wei-min, and Yao Min-li. Iterative diagonally loaded sample matrix inverse robust adaptive beamforming[J].&, 2012, 34(5): 1120-1125.

[13] Li Jian, Stoica P, and Wang Zhi-song. Doubly constrained robust Capon beamformer[J]., 2004, 52(9): 2407-2423.

[14] Lorenz R and Boyd S. Robust minimum variance beamforming[J]., 2005, 53(5): 1684-1696.

[15] Jiang Xue, Zeng Wen-jun, Yasotharan A,.. Robust Beamforming by linear programming[J]., 2014, 62(7): 1834-1849.

[16] Press W, Teukolsky S, Vetterling W,.. Numerical Recipes in C: The Art of Scientific Computing[M]. 2nd Ed. New York: Cambridge University Press, 1992: 456-462.

代保全： 男，1985年生，博士生，研究方向为阵列信号处理、空时自适应信号处理.

王 彤： 男，1974年生，教授，研究方向为机载雷达运动目标检测、合成孔径雷达成像.

同亚龙： 男，1987年生，博士生，研究方向为阵列信号处理、空时自适应信号处理、雷达成像和动目标检测.

吴建新： 男，1982年生，副教授，研究方向为空时自适应信号处理、雷达成像及动目标检测.

保 铮： 男，1927年生，教授，研究方向为自适应信号处理、阵列信号处理、雷达成像和目标识别等.

Robust Adaptive Coherence Estimator Based on Ellipsoid Uncertainty Set Constraint

Dai Bao-quan Wang Tong Tong Ya-long Wu Jian-xin Bao Zheng

(,,710071,)

Adaptive Coherence Estimator (ACE) often suffers considerable performance degradation in the presence of steering vector errors. In this paper, a robust ACE detector based on the ellipsoid uncertainty set constraint is proposed. A detailed analysis of ACE detector is first conducted, which results in an interesting observation that scaling of the steering vector does not affect the statistical test of ACE. With this property exploited, a model for designing robust ACE detector is constructed and is subsequently converted into a convex optimization problem. Then, the solution to the problem is given with the powerful Newton-Raphson method. Simulation results show that the robustness of the proposed detector against the steering vector errors can be improved significantly compared with the standard ACE.

Radar signal processing; Adaptive coherence estimator; Steering vector errors; Ellipsoid uncertainty set; Robust detector

TN957.51

A

1009-5896(2014)12-2969-06

10.3724/SP.J.1146.2014.00563

王彤 twang@mail.xidian.edu.cn

2014-04-30收到，2014-07-03改回

国家自然科学基金(61372133, 61101241)和中央高校基本科研业务费专项资金(K50511020008)资助课题