URANS simulations of ship motion responses in long-crest irregular waves*

SHEN Zhi-rong (沈志荣), YE Hai-xuan (叶海轩), WAN De-cheng (万德成)

State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: zrshen.sjtu@gmail.com

URANS simulations of ship motion responses in long-crest irregular waves*

SHEN Zhi-rong (沈志荣), YE Hai-xuan (叶海轩), WAN De-cheng (万德成)

State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: zrshen.sjtu@gmail.com

(Received November 22, 2013, Revised February 11, 2014)

In this paper, numerical prediction of ship motion responses in long-crest irregular waves by the URANS-VOF method is presented. A white noise spectrum is applied to generate the incoming waves to evaluate the motion responses. The procedure can replace a decade of simulations in regular wave with one single run to obtain a complete curve of linear motion response, considerably reducing computation time. A correction procedure is employed to adjust the wave generation signal based on the wave spectrum and achieves fairly better results in the wave tank. Three ship models with five wave conditions are introduced to validate the method. The computations in this paper are completed by using the solver naoe-FOAM-SJTU, a solver developed for ship and ocean engineering based on the open source code OpenFOAM. The computational motion responses by the irregular wave procedure are compared with the results by regular wave, experiments and strip theory. Transfer functions by irregular wave closely agree with the data obtained in the regular waves, showing negligible difference. The comparison between computational results and experiments also show good agreements. The results better predicted by CFD method than strip theories indicate that this method can compensate for the inaccuracy of the strip theories. The results confirm that the irregular wave procedure is a promising method for the accurate prediction of motion responses with less accuracy loss and higher efficiency compared with the regular wave procedure.

irregular waves, white noise spectrum, unsteady incompressible Reynolds-Average Navier-Stokes (URANS) equations, ship motion response, naoe-FOAM-SJTU solver, OpenFOAM

Introduction

Computational fluid dynamics (CFD) has been one of the most popular tools in the research of ship hydrodynamics in the past decades. CFD can resolve sophisticated physical characteristics of fluid motions and obtain more accurate prediction for ship hydrodynamic performance than the conventional potential theories because it is based on physical models that are more realistic and less simplified. In the field of ship hydrodynamics, CFD can accurately predicate ship hydrodynamic performance even for high speedships and big blunt ships, for which the potential theories suffer from large accuracy loss.

The research of ship seakeeping by CFD can be divided into two parts: regular and irregular waves. The regular wave procedure is usually used to validate the computational methods, predict response amplitude operator (RAO) of ship in one specified frequency, including amplitude and phase, and investigate the high-order nonlinear components. The application of regular wave is usually used to analyze the nonlinear effects on the ship hydrodynamic performances, such as slamming, wave breaking, green water on deck, etc.. In the past decade, many works have focused on the simulation of ship motion related to regular waves with fluid-structure interaction. Orihara and Miyata[1]studied a container ship in head waves based on overlapping grid system to investigate added resistance and motion responses. Carrica et al.[2]performed a verification and validation analysis of a surface combat ship DTMB model 5512 in head wave. The overset grid method was adopted to treat the large-amplitude motion of ship. Yang et al.[3]simulated interactions of extreme waves and an LNG carrier with fullyor partially filled tanks by the VOF method. An arbitrary Lagrangian-Eulerian (ALE) scheme combined with the moving mesh technique was used to deal with ship movement.

The other part of CFD computation of seakeeping is based on irregular waves. The irregular wave procedure can be applied to simulate the real sea conditions. It can also be used to predict ship motion responses in waves by spectral analysis. Carrica et al.[4]simulated short-crest irregular waves by using the Bretschneider spectrum to study broaching event in high sea state. An autopilot was implemented to control the rudder angle and propeller rotation to keep the heading angle. Mousaviraad et al.[5]developed two wave group procedures, transient wave group (TWG) and harmonic wave group (HWG) to predict RAOs. Validation and comparison were completed with the DTMB model 5512 at four speeds.

The aim of this paper is to develop an irregular wave procedure to predict the motion responses of ship in waves. Instead of carrying out a coupled computation of several single regular wave conditions, this procedure just performs a single run to predict the whole curves of RAOs. Hence, the computational time can be considerably saved. The irregular wave procedure can achieve good results with the same accuracy as the regular wave does compared with experimental data. The irregular waves are generated by a white noise spectrum with the superposition of a set of linear waves. The white noise, which does not exist in natural sea environment, has a flat curve in the range of working frequencies where the amplitude of the wave frequencies is constant. This spectrum is designed to predict the motion responses of ship, widely used in experiments in physical wave tanks.

Three ship models with distinct hull shapes are chosen to validate the CFD method. The models include the slender Wigley Hull, the container ship S-175 and the fast surface combat ship DTMB 5512. The Froude number ranges from 0.25 to 0.41. In this paper, although the linear waves are applied, which can be easily solved by potential theories, the CFD aproach can maintain better results in a wide range of ship speeds, especially for high Froude number. The CFD method can also achieve good prediction of ships with blunt shapes or complex geometries.

The computations in this paper are performed with the naoe-FOAM-SJTU, a solver developed for hydrodynamics of ship and ocean engineering based on the open source code OpenFOAM. In our previous work, the validations of resistance of benchmark ships fixed in calm water[6]and predication of motion response and added resistance in head regular wave[7]has been performed. Good agreements with experiments were achieved in the previous work. This solver utilizes the data structure and CFD libraries in the OpenFOAM, including FVM, RANS, VOF and PISO algorithm. New modules have been developed, including wave generation and damping, six-degree-offreedom (6DOF), etc..

1. Numerical methods

1.1Governing equations

An unsteady incompressible Reynolds-Average Navier-Stokes (URANS) equations coupled with the volume of fluid (VOF) method is adopted in this paper:

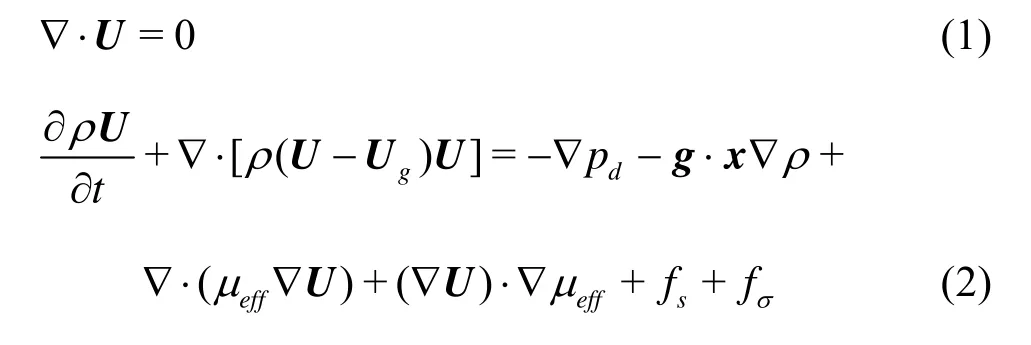
whereUis velocity field andUgis the grid velocity,pdthe dynamic pressure field,ρthe mixture density,gthe gravitational acceleration vector,μeff=ρ(ν+νt) the effective the dynamic viscosity, in whichνandtνare mixture kinematic viscosity and eddy viscosity, respectively,fσthe surface tension term,fsthe source term of sponge layer, which will be discussed in the following section.tνis obtained by the SST turbulence model[8]for turbulence closure. The URANS equations are discretized by the finite volume method, and solved by the pressure-implicit with splitting of operator (PISO) algorithm.

A VOF method with artificial compression technique is applied[9,10]

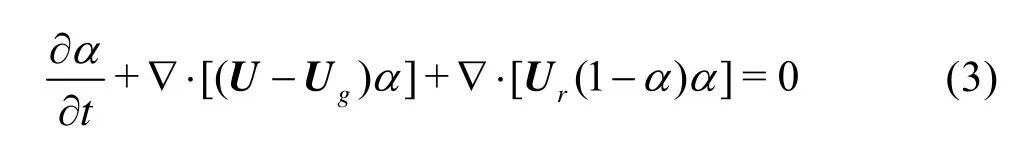
whereαis volume of fraction, the relative proportion of fluid in each cell.α=0 if cell is located in air andα=1 in water. If the cell is crossing the interface, 0＜α＜1. The third term in Eq.(3) is the artificial compression term, taking effects only on the interface due to the term (1-)α α.Uris the velocity field used to compress the interface, of which the expression the expression can be found in Ref.[10].

The surface tension term in Eq.(2) is defined as

whereσ=0.07 kg/s2is the surface tension coefficient, andκis the curvature of surface interface andαis volume of fraction, determined by VOF equation.

1.2Wave generation and damping

The irregular waves are assumed as a superposition of a series of linear waves.

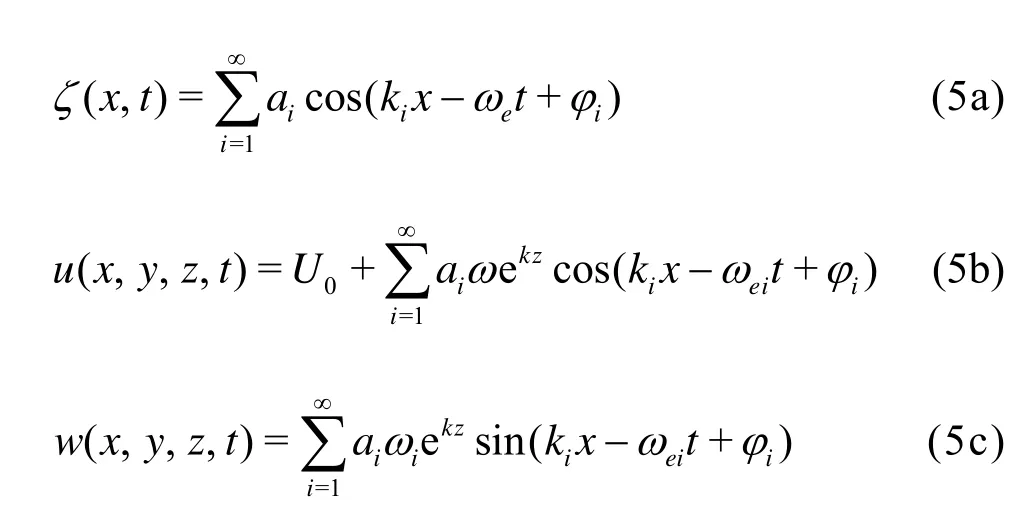
in which,ζ(x,t) is the transient wave elevation, the subscriptithe index of each wave components,aiis the wave amplitude,kithe wave number,iωthe natural frequency of wave,ωeithe encounter frequency, given byωei=ωi+kiU0whereU0is the velocity of ship.

The wave generation method is to impose the boundary conditions ofαin VOF Eq.(3) andU(u,v,w) in the URANS Eq.(2). The expressions ofu,win Eq.(5) can be directly adopted as the Dirichlet condition forU(u,v,w). However, the boundary condition forαis more complicated. If the cell face in the boundary located below the transient wave elevationζ(x,t),α=0, otherwise,α=1. If the cell face is crossing withζ(x,t),αcan be calculated by

whereS0is the total area of the cell face andSwis the area of the part belowζ(x,t).

The generation of irregular wave is based on the wave spectrumS(ωe) and the amplitude of each component can be calculated by

Before the numerical simulation is carried out, a step of wave spectrum correction is performed in the numerical wave tank without ship hull.

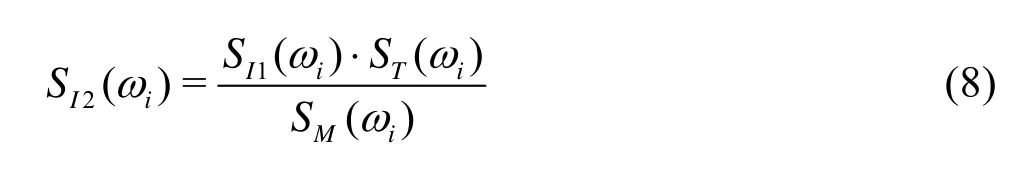
whereSI1(ωi) is the current input spectrum,SI2(ωi) is the new corrected spectrum used to generate the irregular wave in the next period,ST(ωi) the target spectrum andSM(ωi) the measured spectrum recorded by a wave height probe in wave tank, as shown in Fig.1. In additions, a relaxation factor is introduced in this process in order to improve the stability and convergence of this algorithm

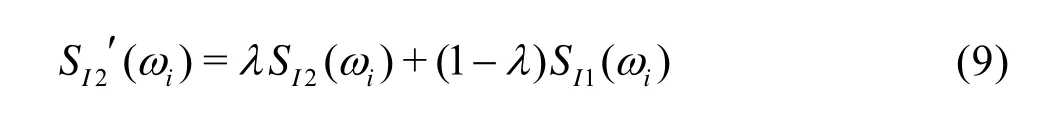
The solution comes to convergence after performing 3-5 iterations. The measured spectrum closely agrees with the target.

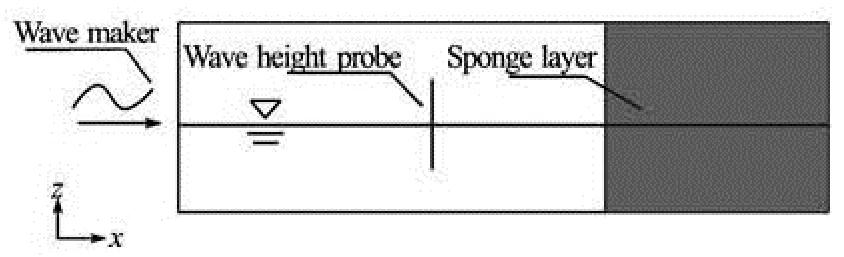
Fig.1 Layout of the numerical wave tank

The results of heave and pitch motions are processed by Fourier analysis. The frequency of each wave component can be defined as:fi=niff, where,ffis the fundamental frequency andniis a positive integer. A sampling period is defined as:Ts=1/ff.Tscovers the integral multiple of all periods of wave components. The spectral leakage is ideally zero if window functions are simply used over a periodTs. Therefore, the 1st order linear harmonic amplitude of each frequency can be calculated by the integration over the periodTs:

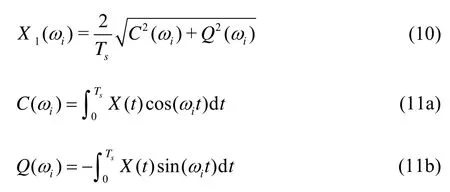
whereξ(t) are the transient results to be analyzed, such as heave and pitch motions.

A sponge layer is setup at the end of the tank to absorb the wave reflection. The sponge layer method was used in previous work and had good effects[11,12]. A source termfsadded in Eq.(2) is denoted as:

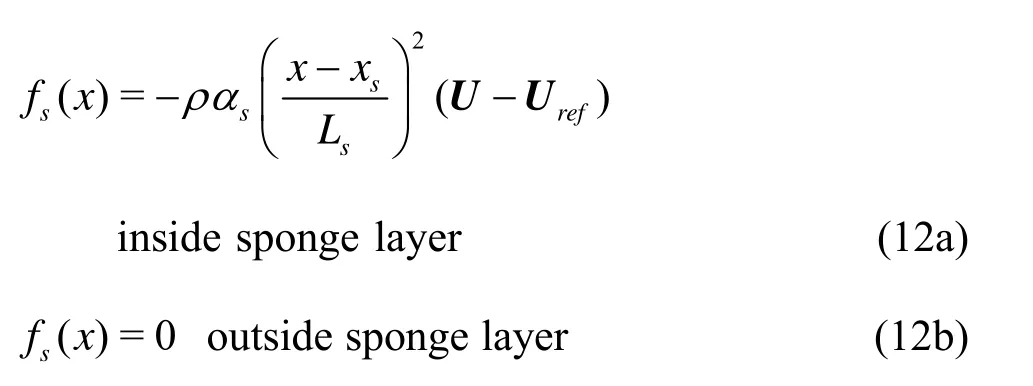
wherexsis the start position of sponge layer,xthe positions of mesh cells located in sponge layer,Lsthe length of layer,sαan artificial viscosity coefficient to control wave damping effect, which is 20 in current study.Urefis a reference velocity to dampen velocity at the exit toUref·Urefis equal to the inlet velocity to keep mass conversation of global computational domain. The layout of the numerical tank with the wave maker, the sponge layer as well as the wave height probe are demonstrated in Fig.1.

Fig.2 Demonstration of two coordinate systems

1.36DOF module and coordinate systems

A fully 6DOF module has been developed in our previous work[7]to predict the motions of ship in regular waves. This method utilizes two coordinate systems to compute and predict ship motions as shown in Fig.2. The coordinate system of the computational domain is the earth-fixed system (x,y,z), which is an inertial system moving at a constant ship speedU0. The coordinate system has the origin located at the fore perpendicular. Thex-axis points along the longitudinal direction from head to stern,y-axis is in starboard direction andz-axis points vertical upwards with water line located atz=0. An other coordinate system (x＇,y＇,z＇) is fixed with ship with the origin fixed at the rotation center of the ship. At the initial condition, the system parallels with the earth system, but translates and rotates with movement of ship. The forces and moments are computed in the earth system and then they are transformed to ship-fixed system to solve the rigid body equations:

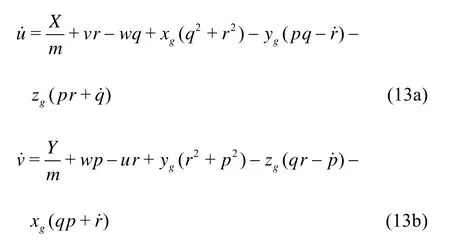
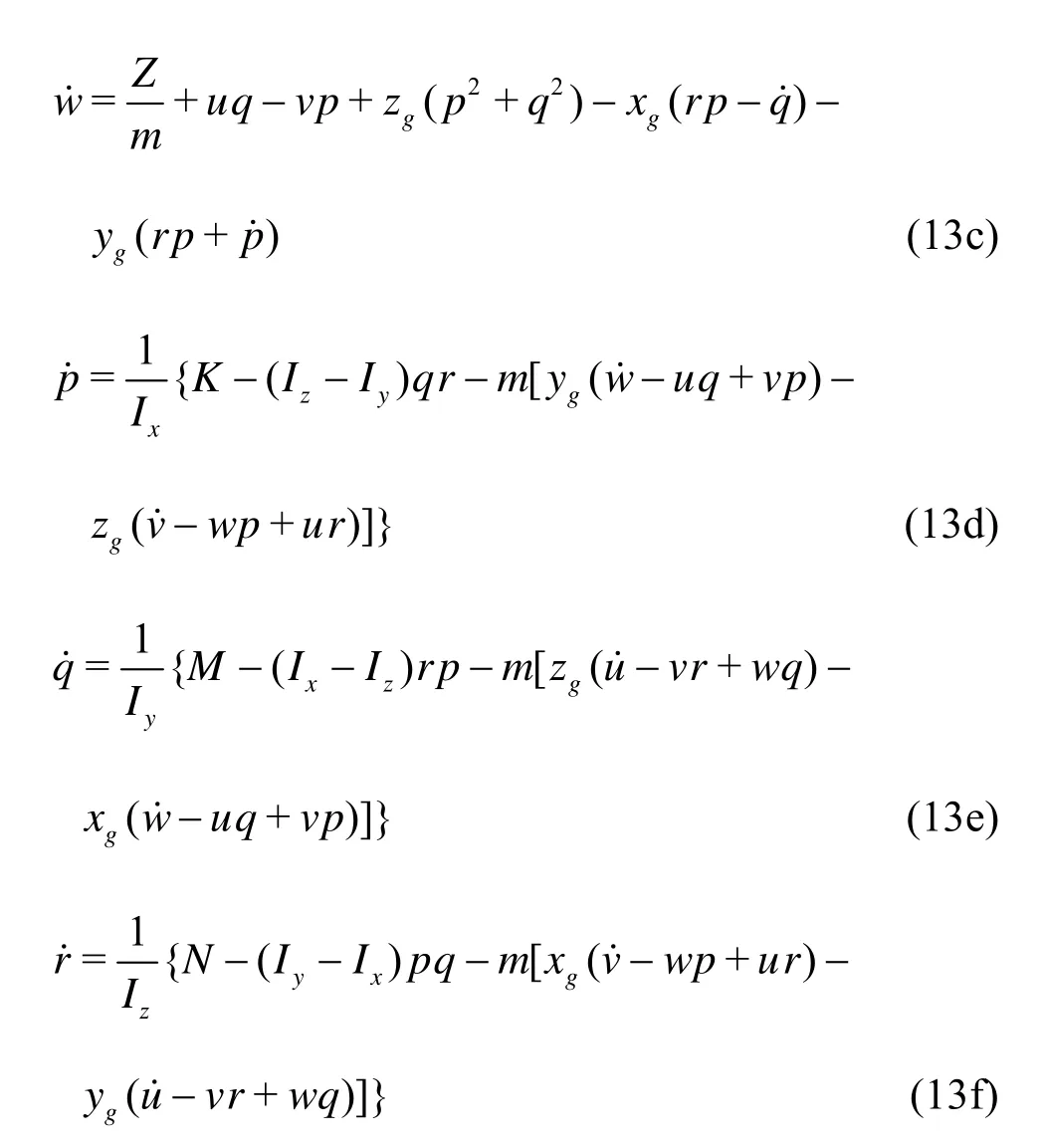
The obtained accelerations are integrated over time to get velocities, which are projected to earthfixed system later. The predicted velocities are sent to the mesh motion solver to compute the positions of mesh nodes for the next time step. The detailed procedure of the 6DOF solver can be found in Ref.[7].

2. Geometries and conditions

In order to validate the irregular wave approach, three different types of ship models are involved in this study, the Wigley hull, S-175 and DTMB 5512. The three models represent three different ship types. The Wigley hull is a slender body, S-175 is a container ship and DTMB 5512 is a fast surface combat ship with a sonar dome and a transom stern. The Froude numbers for all the cases range from 0.25 to 0.41. The different types and speeds are chosen in order to prove the robustness and flexibility of the current approach. The motion responses of heave and pitch of the three models are computed by the irregular wave procedure. In additions, the computations of wave regular condition are also included to compare with the regulars obtained by irregular waves. All the computational results are compared with those given with existing measurements and strip method.

2.1Wigley

The first model adopted for validation is a modified Wigley hull. The vertical motions of four modified Wigley hulls in head wave are investigated experimentally by Journée[13]. The model III, which is closest to the original Wigley hull, is chosen for simulation in this paper. Two speeds are performed in thiswork withFr=0.30 and 0.40. The principle dimensions of the hull are shown in Table 1.

Table 1 Principle dimensions of modified Wigley hull[14]

Fig.3 Geometry of S-175 container ship

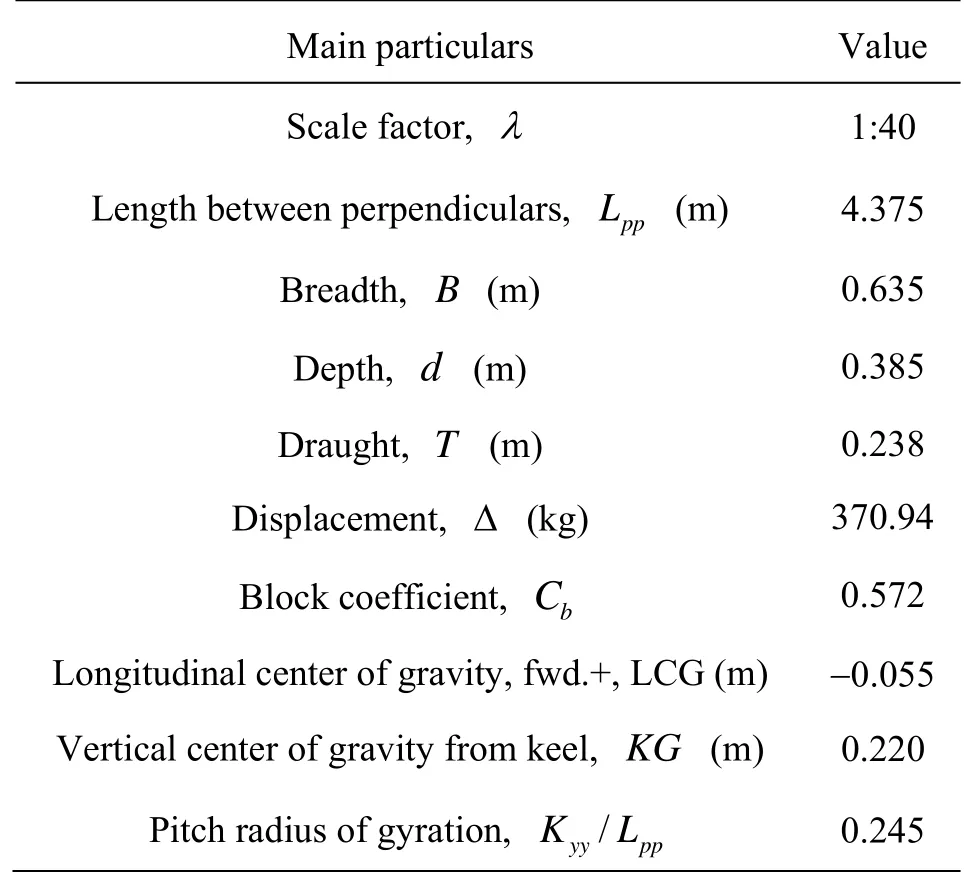
Table 2 Main particulars of S-175 ship model[14]

2.2S175

The S-175 was used for the comparative numerical study of wave-induced vertical motions and wave loads during the 15th and 16th ITTC Seakeeping Committees. The ship is a modern container ship with a bulbous and a block coefficient of 0.572. Fonseca and Guedes Soares[14,15]carried out the experimental and numerical studies of the nonlinear vertical motion and loads on this model in regular head waves with different wave lengths and wave steepness. A scale factor of 1:40 was adopted in the experiment and the Froude number of model ship isFr=0.25. The main particulars of the ship model used in present work are presented in Fig.3 and Table 2.

Fig.4 Geometry of DTMB model 5512

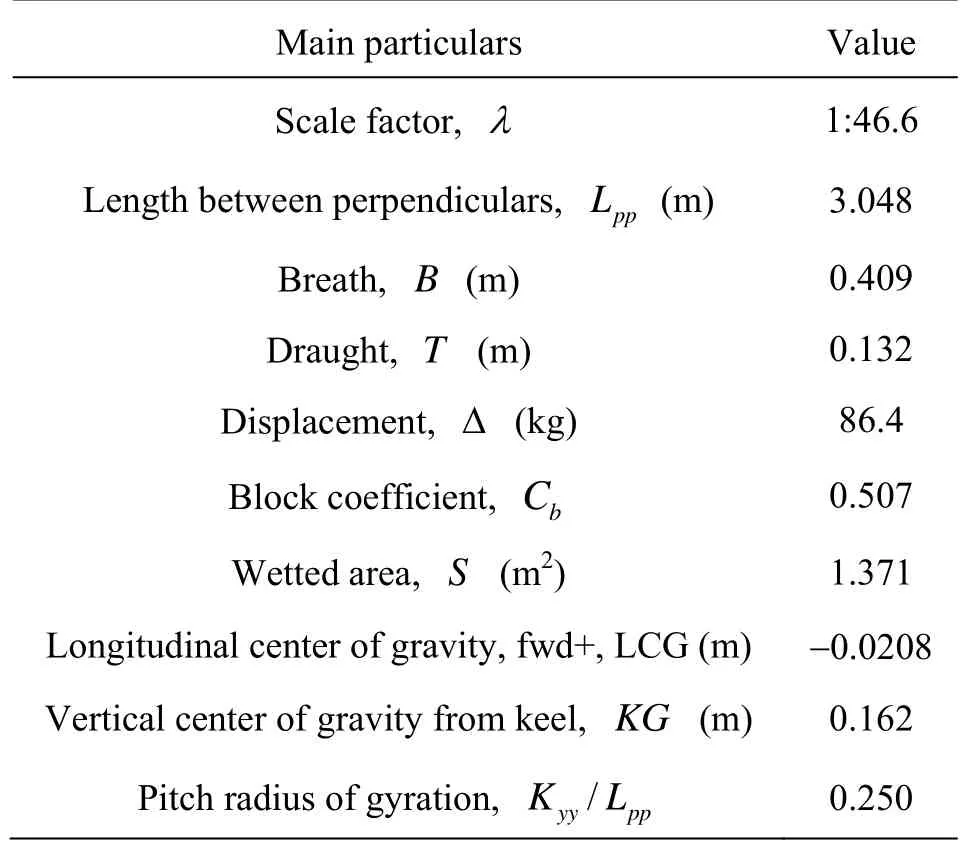
Table 3 Geometrical properties of DTMB Model 5512[16]

2.3DTMB model 5512

The third model ship is David Taylor Model Basin (DTMB) model 5512. This model was conceived a preliminary design for USA Navy surface combatant. It has been adopted as a recommended benchmark for CFD validation in the latest Ship Hydrodynamics CFD Workshops in Gothenburg in 2010. This model has a sonar dome and transom stern. with scale of 1:46.6 and lengthL=3.048 m. Irvine et al.[16]performed the experiments of DTMB 5512 free to heave and pitch in head waves, providing experimental data and strip method results for CFD validation. Figure 4 and Table 3 show the geometry and principal dimensions of the model. Two ship speeds are investigated in this paper, medium speed (Fr=0.28) and high speed (Fr=0.41).

2.4Irregular wave conditions

All the irregular waves in this study are generated through the white noise spectrum. Table 4 summaries the irregular wave conditions for all cases, wherefe,minandfe,maxrepresents the range of working frequency,S0is a constant spectral density in working range andHsis the significant wave height, estimated by

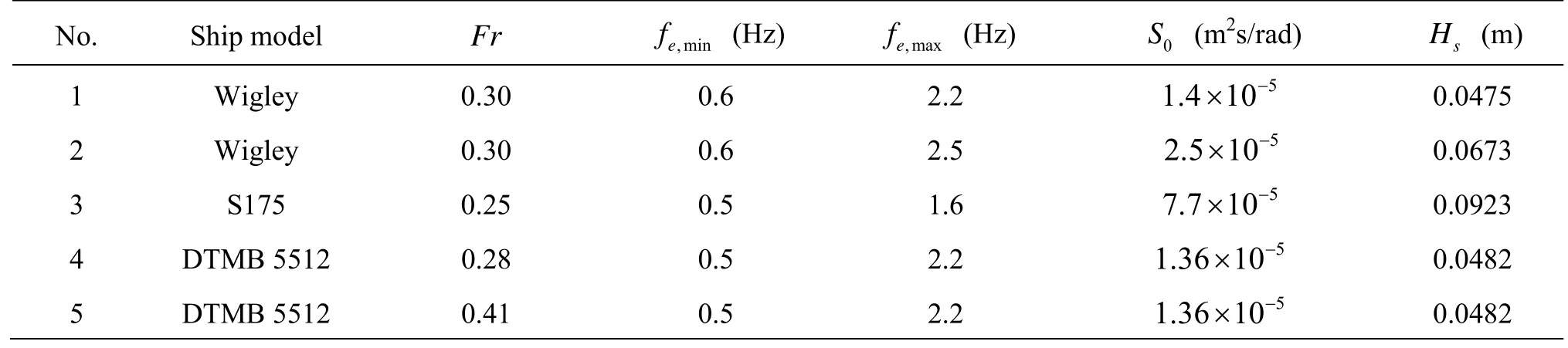
Table 4 Summary of irregular wave conditions (in model scale)

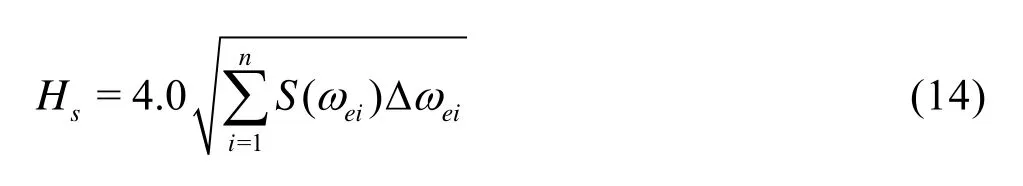
S0is set to be a small value in order to avoid nonlinear motions of ship, which affects accuracy of the irregular wave procedure. All cases hasd fe=0.1 Hz and andTs=1/d fe=10 s .

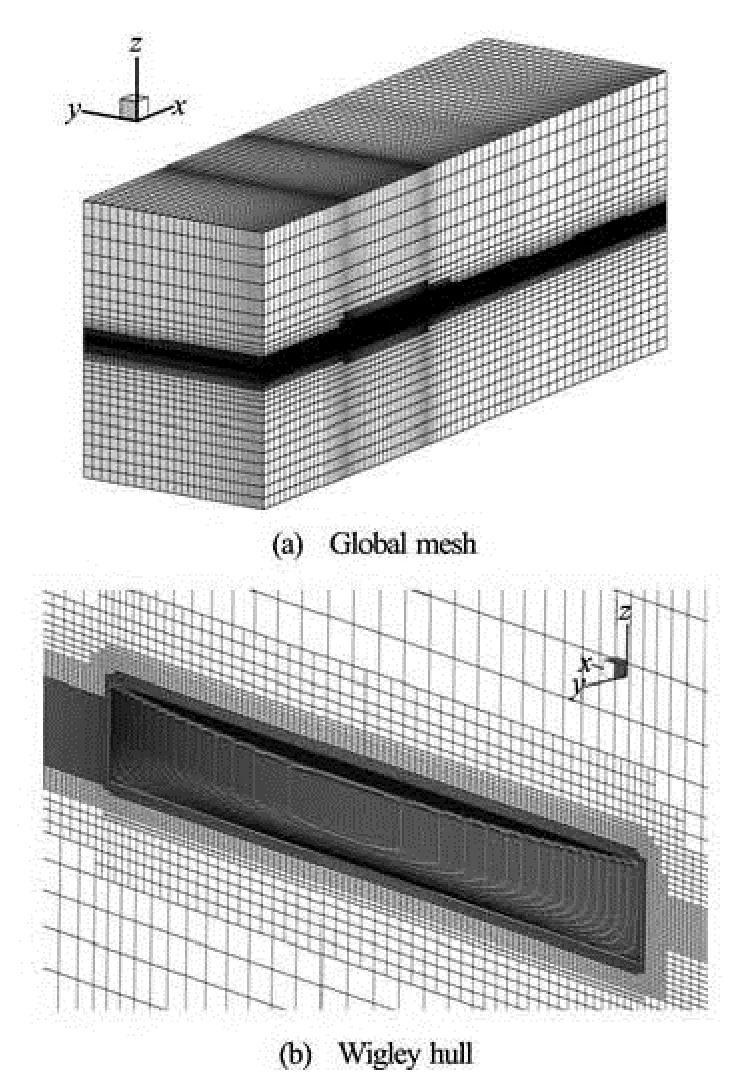
Fig.5 Global mesh and local mesh for Wigley hull mesh

2.5Meshes

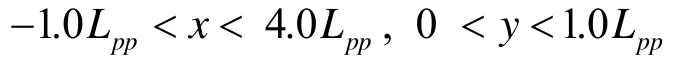
Fig.6 Local mesh for S175 container ship

Fig.7 Local mesh for DTMB model 5512

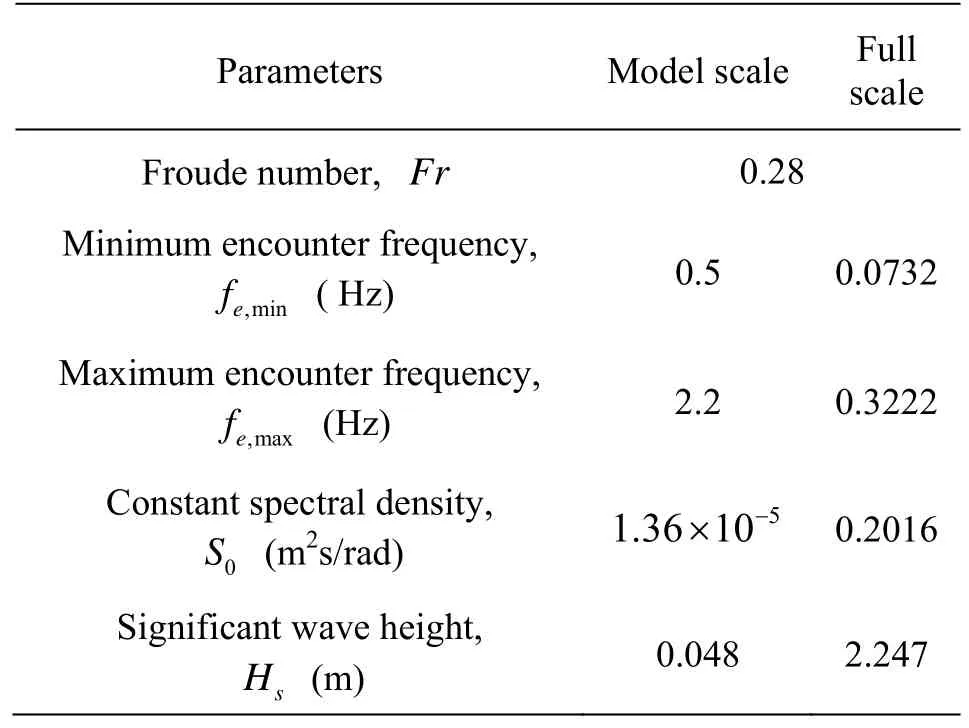
Table 5 Parameters of white noise spectrum of DTMB 5512 atFr=0.28

Fig.8 Comparison of measured corrected wave spectrum with the target (full scale)

3. Results

3.1Irregular wave generation and correction

The wave condition of DTMB model 5512 is taken for example to validate the wave generation and correction procedure. The parameters of white noise spectrum are listed in Table 5. The results of the measured wave spectrum by wave height probe are shown in Fig.8. The spectrum is measured at the longitudinal location of ship’s center of gravity. The dashed line presents the initial uncorrected spectrum recorded by wave probe. Severe oscillation and deviation from the target at the working frequency are observed. However, the new spectrum (solid line) is achieved after the wave maker signals have been adjusted according to Eqs.(8) and (9) Compared with the uncorrected one, the corrected spectrum precisely matches the target. Figure 9 illustrates time histories of wave elevation measured by the wave height probe after the correction step is converged. The measured elevation closely agrees with the analytic one and no noticeable discrepancy has been observed. The results indicate a large improvement over the wave spectrum measured by the correction step, providing incoming wave with high quality for the simulation of seakeeping.

3.2Motion responses

Figure 10 hows the time histories of heave and pitch motions for DTMB 5512 atFr=0.41 over 2Ts. The histories are processed by Eq.(10) to obtain the first-order harmonic amplitude of have and pitch,X3i,X5i. We define the transfer functions of heave and pitch motions as

where the subscriptidenotes the index of each wave component,TFx3iandTFx5iare the transfer functions of heave and pitch motions, the results of which are shown in Figs.11-15.

Figures 11 and 12 present the transfer functions of the Wigley hull atFr=0.30 and 0.40. The results obtained by irregular waves are compared with existing experimental data, strip theory and other results by regular wave. The data of regular wave are also achieved by naoe-FOAM-SJTU, but in regular wave. The data of experiment and strip theory are provided by Journée[13]. The computational results for both irregular and regular waves agree very well with the experiment data at bothFr=0.30 andFr=0.40. The differences between the results of irregular and regular are small except forTFx5atfe=1.08 Hz, whereTFx5by regular wave is overpredicted. The CFD methods give better results than the strip theory. Poor results were obtained by the strip theory for the pitch motion at the two speeds, while the CFD methods can predict both heave and pitch motions well agreed with measurements. The peaks ofTFx3andTFx5occur atfe=1.1 Hz atFr=0.30. AtFr=0.40,TFx3shows peak atfe=1.2 Hz whileTFx5reaches maximum atfe=1.0 Hz. In low frequency range (fe＜0.7 Hz), bothTFx3andTFx5are close to 1.0 while at high frequency range (fe＞1.5 Hz), they are approaching to zero.

Figure 13 illustrates the results for S-175 model. The experiments were performed by Fonseca and Guedes Soares[15]in regular head waves atFr=0.25.

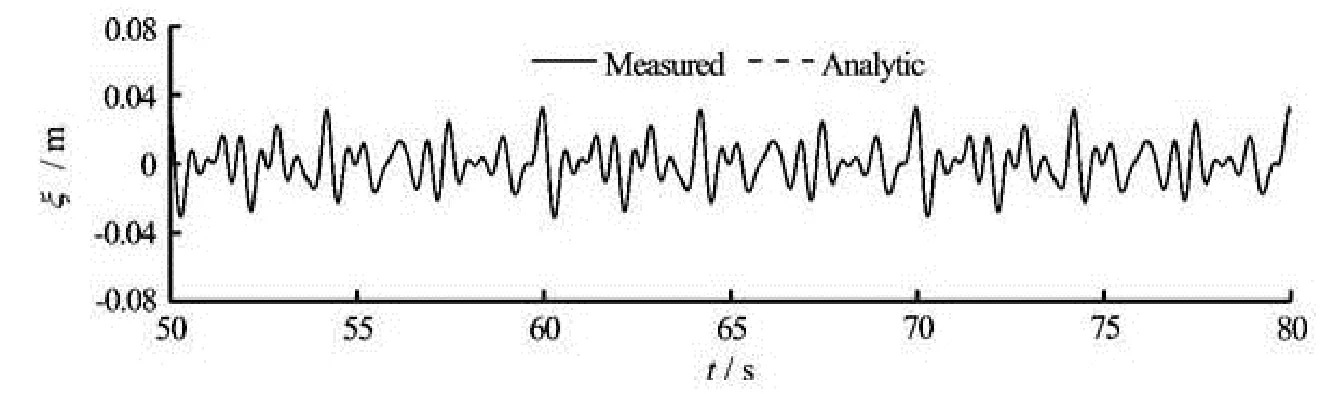
Fig.9 Measured wave elevation after correction, compared with analytic result

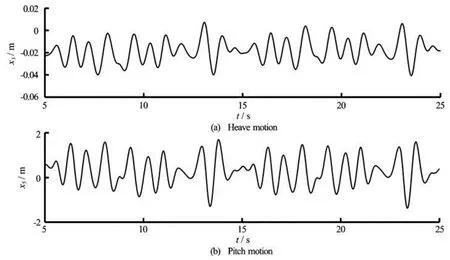
Fig.10 Time histories for heave and pitch motions for DTMB 5512 atFr=0.41 over two sampling periods

Fig.11 Comparison of transfer functions atFr=0.30 for Wigley hull

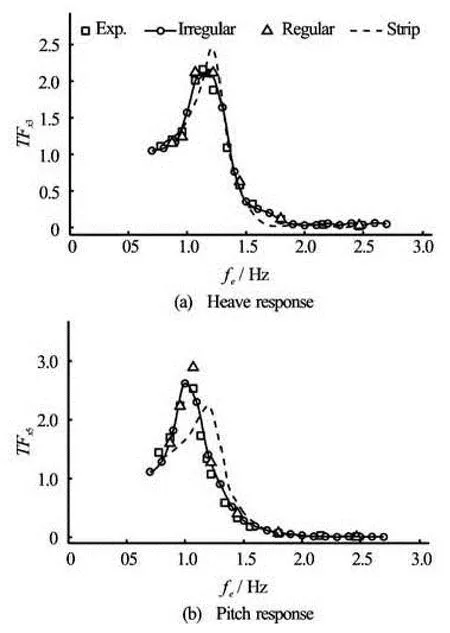
Fig.12 Comparison of transfer functions atFr=0.40 for Wigley hull

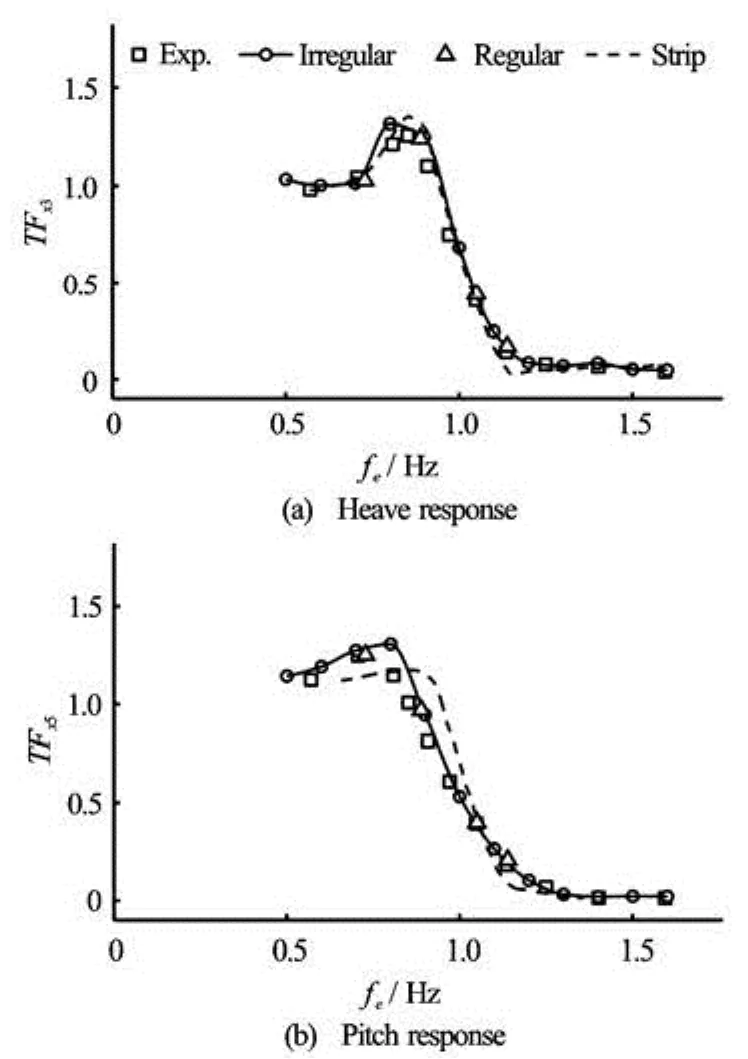
Fig.13 Comparison of transfer functions atFr=0.25 for S175

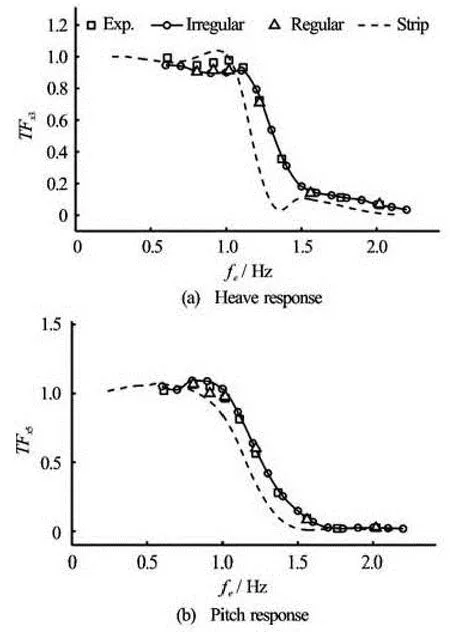
Fig.14 Comparison of transfer functions atFr=0.28 for DTMB model 5512

The wave steepness ofHw/Lw=1/80 is used in this study, whereHwis the wave height andLwis the wave length. The results by strip theory was given by a nonlinear time domain strip method[16]. The transfer functions achieved by the irregular waves are compared with the results in regular waves forHw/Lw=1/ 80. As is shown in the figure, the computational data by both irregular and regular fairly agree with experimental results. However, the peaks of bothTFx3andTFx5are larger than those in the experiment. According to the experiment, the transfer functions of S-175 are sensitive to wave steepness and nonlinear components have large effect on peak value. Because the wave amplitudes generated by white noise spectrum are identical, it is difficult to keep wave steepness of all wave frequencies identical to that in the experiments. The results indicate good agreements between irregular wave and regular wave. Similar with the results of the Wigley Hull, the strip theory agrees well with experiment for heave motion, but larger discrepancies are observed for pitch motin.

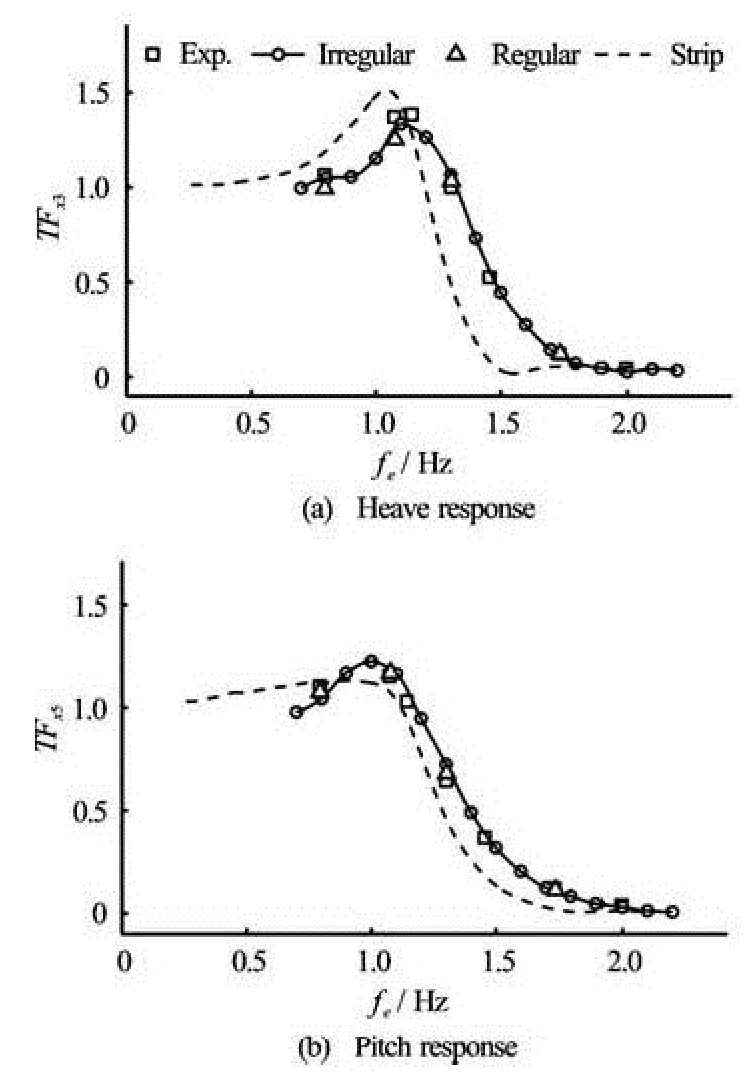
Fig.15 Comparison of transfer functions atFr=0.41 for DTMB model 5512

Figures 14 and 15 present the transfer functions for DTMB 5512 atFr=0.28 andFr=0.41, respectively. The experimental results were from Irvine et al.[16]with =0.025

ak, whereais wave amplitude andkis wave number. The experiments also provided results by a linear strip theory from the ship motions program (SMP). The results by regular wave are included here to validate the irregular wave method. AtFr=0.28, the computational results in irregular and regular waves closely agree with experiments, but discrepancies occur atfe＜1 forTF3. The results forFr=0.41 show much better comparison thanFr= 0.28. Good agreements are obtained between irregular and regular waves, indicating that the irregular waveprocedure can obtain as good results as in the regular wave. The linear strip method shows the same trend as experiments, but still presents larger errors than CFD predication. It may be due to the complex geometry of this model. At higher speed (Fr=0.41), the irregular wave procedure can hve good agreement compared with experiments while the strip theory presents larger errors compared with the case of lower speed (Fr= 0.28).

Fig.16 Snapshots of wave surface of all cases

Figure 16 illustrates the wave patterns for all three ships in different wave conditions. It is difficult to compare wave patterns among different ship models on the same condition since the incoming wave is irregular. Herein it is just a simple demonstration of ship moving in irregular waves. All of the figures are captured att=12.0 s. The induced waves show much difference due to the different bow shape. The ship speeds also influence bow waves. For the DTMB model 5512 atFr=0.41, a distinct overturning of bow wave is clearly observed due to the highest speed.

4. Conclusions

The purpose of this paper is to present an irregular wave procedure to predict the motion responses of ship in waves. This procedure can obtain the whole responses curves by a single run instead of a decade of runs in regular waves so that the computational time can be considerably saved. The procedure can obtain as good motion responses as in regular waves with less accuracy loss compromised.

Three different types of ship models model in five irregular wave conditions have been performed to validate presented methods, including the slender Wigley Hull, the container ship S-175 and the surface combat DTMB 5512. Good agreements between regular and irregular wave procedures are achieved, indicating that less accuracy loss is resulted for the irregular wave method. The computational results by irregular wave procedure closely agreed with the measurements even forFr≥0.40, showing the robustness and flexibility of the CFD method at high speed. The CFD method can obtain higher accuracy at higher Froudenumber and for complex geometry although the potential theories can also handle the linear waves applied in the work.

Future work will focused on the seakeeping problem in irregular waves including short-crest waves and nonlinear waves. More emphasis will placed on the large-amplitude waves to investigate the nonlinear effects of nonlinear waves and the nonlinear interactions with ships in 6DOF motions in a rough sea.

Acknowledgements

This work was supported by the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning (Grant No. 2013022), Center for HPC of Shanghai Jiao Tong University, and Lloyd’s Register Foundation (LRF), a charitable foundation, helping to protect life and property by supporting engineering-related education, public engagement and the application of research.

[1] ORIHARA H., MIYATA H. Evaluation of added resistance in regular incident waves by computational fluid dynamics motion simulation using an overlapping grid system[J].Journal of Marine Science and Technology,2003, 8(2): 47-60.

[2] CARRICA P. M., WILSON R. V. and NOACK R. W. et al. Ship motions using single-phase level set with dynamic overset grids[J].Computers and Fluids,2007, 36(9): 1415-1433.

[3] YANG Chi, LÖHNER Rainald and LU Haidong. An unstructured-grid based volume-of-fluid method for extreme wave and freely-floating structure interactions[J].Journal of Hydrodynamics,2006, 18(3 Suppl.): 415-422.

[4] CARRICA P. M., PAIK K. J. and HOSSEINI H. S. et al. URANS analysis of a broaching event in irregular quartering seas[J].Journal of Marine Science and Technology,2008, 13(4): 395-407.

[5] MOUSAVIRAAD S. M., CARRICA P. M. and STERN F. Development and validation of harmonic wave group single-run procedure for RAO with comparison to regular wave and transient wave group procedures using URANS[J].Ocean Engineering,2010, 37(8-9): 653-666.

[6] SHEN Z. R., JIANG L. and MIAO S. et al. RANS simulations of benchmark ships based on open source code[C].Proceedings of the Seventh International Workshop on Ship Hydrodynamics.Shanghai, China, 2011, 76-82.

[7] SHEN Z. R., WAN D. C., RANS computations of added resistance and motions of a ship in head waves[J].International Journal of Offshore and Polar Engineering,2013, 23(4): 263-271.

[8] MENTER F. R. Review of the shear-stress transport turbulence model experience from an industrial perspective[J].International Journal of Computational Fluid Dynamics,2009, 23(4): 305-316.

[9] RUSCHE H. Computational fluid dynamics of dispersed two-phase flows at high phase fractions[D]. Doctoral Thesis, London, UK: Imperial College, 2002.

[10] BERBEROVIĆ E., Van HINSBERG N. and JAKIRLIĆ S. et al. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution[J].Physical Review E,2009, 79(3): 36306.

[11] CAO H. J., WAN D. C. Development of multidirectional nonlinear numerical wave tank by naoe-FOAMSJTU solver[J].International Journal of Ocean System Engineering,2014, 4(1): 52-59.

[12] SHEN Z. R., WAN D. C. Numerical simulation of sphere water entry problem based on VOF and dynamic mesh methods[C].Proceedings of the 21st International Offshore and Polar Engineering Conference.Maui, Hawaii, USA, 2011, 695-702.

[13] JOURNÉE J. M. J. Experiments and calculations on 4 Wigley hull forms in head waves[R]. Report 0909, The Netherlands, Delft: Ship Hydromechanics Laboratory, Delft University of Technology, 1992.

[14] FONSECA N., GUEDES SOARES C. Experimental investigation of the nonlinear effects on the vertical motions and loads of a containership in regular waves[J].Journal of Ship Research,2004, 48(2): 118-147.

[15] FONSECA N., GUEDES SOARES C. Comparison between experimental and numerical results of the nonlinear vertical ship motions and loads on a containership in regular waves[J].International Shipbuilding Progress,2005, 52(1): 57-89.

[16] IRVINE M., LONGO J. and STERN F. Pitch and heave tests and uncertainty assessment for a surface combatant in regular head waves[J].Journal of Ship Research,2008, 52(2): 146-163.

10.1016/S1001-6058(14)60050-0

* Project supported by the National Natural Science Foundation of China (Grant Nos. 51379125, 11272120), the National Key Basic Research Development Program of China (973 Program, Grant No. 2013CB036103) and the High Technology of Marine Research Project of the Ministry of Industry and Information Technology of China.

Biography: SHEN Zhi-rong (1987-), Male, Ph. D. Candidate

WAN De-cheng,

E-mail: dcwan@sjtu.edu.cn