基于Allan方差的光纤陀螺随机漂移建模与仿真

金 毅，吴训忠，谢 聂

（空军工程大学 航空航天工程学院，陕西 西安710038）

引言

光纤陀螺（FOG）是光纤传感领域主要成就之一，它具有动态范围广、寿命长、启动快、抗冲击等优点，在航空、航天和航海领域得到广泛应用。由于FOG的元件特性等原因，在FOG的输出信号中存在较大的随机漂移［1］，因此建立FOG随机漂移误差模型以便在滤波中加以补偿就显得非常重要，已有的FOG随机漂移误差建模方法可分为3种：1）基于统计量的随机漂移误差建模，用该方法建模后物理意义明确，但存在缺陷：由实验数据精确地确定自相关函数等统计量需花费很长时间［2］；2） 建 立 时 间 序 列 模 型 （ARMA 模 型 ）。IEEE规定的陀螺标准［3］指出：用ARMA建立的模型，会存在模型敏感性的问题，需要大量数据对其进行训练。文献［4］指出：ARMA模型并不适合奇功率过程和高阶过程，而FOG随机漂移中存在以上2种过程，只是因为其影响较小，在用ARMA模型建模时忽略了其存在；3）用微分方程建立随机漂移误差模型。此类建模是把陀螺中的随机漂移误差分为白噪声和有色噪声的组合［5］，它具有以下优势：1）它把白噪声过程从随机漂移中分离出来，便于滤波时处理；2）用微分方程表示的随机漂移有色噪声项，可直接并入惯导误差方程，便于计算。

采用基于随机漂移误差辨识的微分方程建模方法。首先用Allan方差辨识FOG静态输出数据，确定其中有色噪声和白噪声参数，然后为每一种有色噪声提供微分方程描述。在建模时使用白噪声驱动的线性微分方程来模拟各个有色噪声，组合白噪声、量化噪声和各个有色噪声，得到最终模型。

1 FOG随机漂移的辨识

FOG中随机漂移误差的辨识是指：在静态下分析FOG的输出数据，判断出FOG中随机漂移的成分及其具体参数。在陀螺中存在的主要随机漂移成分为白噪声、量化噪声、零偏不稳定性、随机游走、斜坡误差［6］，文中采用Allan方差分析法辨识出上述5种噪声的具体参数。

1.1 Allan方差分析法

Allan方差分析法［7］是基于时域的分析法，能较为快捷地检测出噪声数据中的各类误差源对整个噪声的贡献情况，分离出各类误差源，并量化各类误差源。

Allan方差法分析过程如下：以采样时间τ0对FOG输出角速率采样，共采样N个点，构成序列｛ωt｝。把这N个采样值分为K 组，一组有M个采样值（M≦（N－1）／2），每组采样所用时间τ＝Mτ0为相关时间，每组平均值为

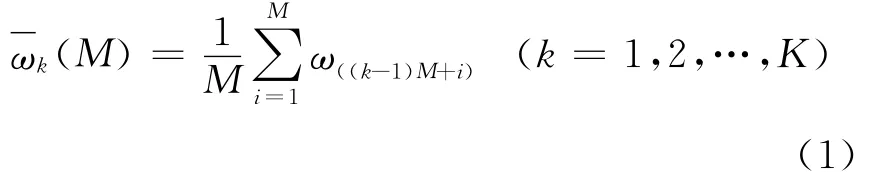
Allan方差定义式：

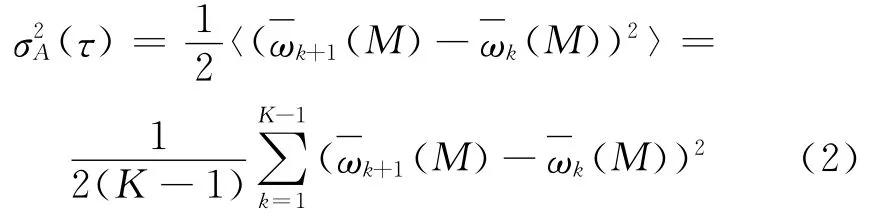
式中〈〉表示总体求平均。

相关时间τ取不同值，得到相应的Allan方差。

采样数据中噪声的双边功率谱密度Sω（f）与Allan方差存在如下关系：

（3）式说明，存在一个传递函数为sin4（πfτ）／（πfτ）2的滤波器，使陀螺仪输出的噪声与Allan方差成正比。因此，Allan方差能够分离、辨识、量化数据中存在的各类噪声项。

1.2 FOG随机漂移误差与Allan方差

FOG中的5种噪声项都有可能存在于FOG输出角速率中，且各个噪声会在τ的不同区域显现出来。因此，Allan方差可辨识并量化出FOG输出角速率中存在的各个噪声项［8］。若各个噪声项在统计特性上是独立的，则Allan方差可表示为各个噪声项的平方和：

由于方差值在一般情况下较小，计算其标准差可提高拟合精度，（4）式近似为

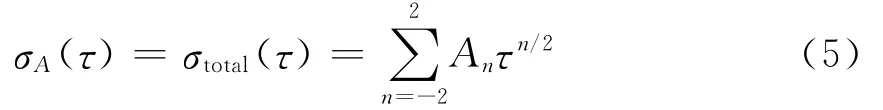
用最小二乘法拟合函数σA（τ），可以求出An。再通过下面的公式，可以得到白噪声N、量化噪声Q、随机游走K、零偏不稳定性B、斜坡误差R，其估计值为

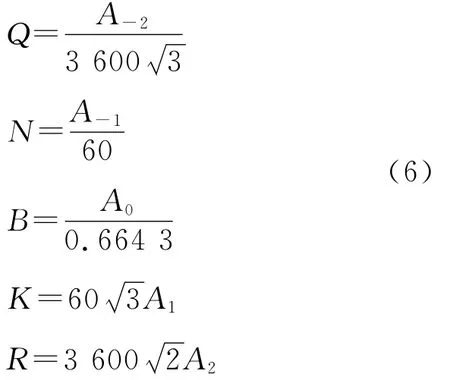
2 漂移误差建模

随机漂移误差建模时，白噪声可以直接作为系统的驱动噪声，不需要进行建模［2］。量化噪声可以转化为等效的白噪声，也无需建模［9］。而为了补偿有色噪声，则需要建立有色噪声模型，特别是输出数据中存在多种有色噪声时，更要建立各个有色噪声模型。对FOG中存在的3种有色噪声：随机游走K、零偏不稳定性B、斜坡误差R的建模过程如下：首先写出各个有色噪声的功率谱密度函数，然后用谱分解定理算出各个有色噪声的传递函数，最后用各个有色噪声的传递函数推导出其微分方程。

2.1 零偏不稳定性建模

零偏不稳定性的功率谱密度函数：

根据方程：

可以得到其成型滤波器的无理函数形式传递数：

零偏不稳定性可用一阶马尔可夫（Markov）过程近似为［3］

经傅里叶逆变换后，得到零偏不稳定性的微分方程表达式：

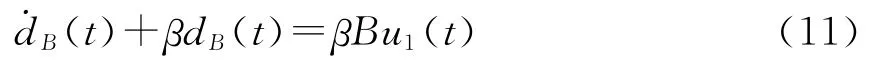
上式中的u1（t）表示单位高斯白噪声。β取5Hz时，可使上式的幅值误差小于－3dB［5］。

2.2 随机游走建模

随机游走的功率谱密度函数：

根据（8）式可得到其成型滤波器传递函数：

上式傅里叶逆变换后，得到随机游走的微分方程表达式：

上式中的u2（t）表示单位高斯白噪声。

2.3 斜坡误差建模

斜坡误差的功率谱密度函数为

根据（8）式可得到其成型滤波器的无理传递函数：

斜坡误差可用二阶马尔可夫过程近似，得到成型滤波器传递函［3］：

（17）式傅里叶逆变换后，得到斜坡误差的微分方程：

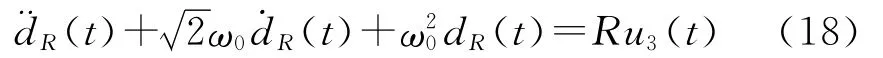
考虑到斜坡误差的低频特性，取ω0等于0.05rad／s，则近似传递函数＾GR（jω）的幅值误差小于－3dB。

2.4 总体方程确立

用Allan方差辨识FOG静态输出数据，确定其中白噪声、量化噪声和3种有色噪声参数后，将5组互不相关的单位高斯白噪声作为驱动噪声输入到5组建立的噪声方程中，建立的噪声方程的系数采用Allan方差辨识出的参数，把5组方程的输出值相加，得到最终模型，其原理如图1所示。

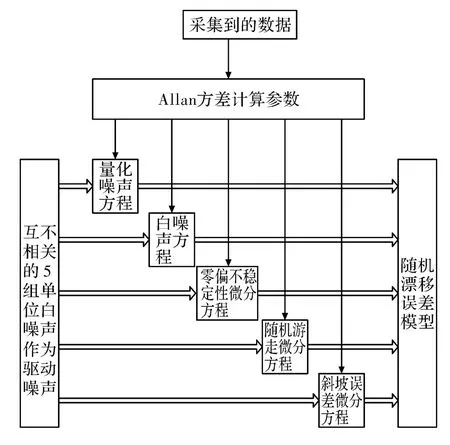
图1 随机漂移误差建模原理如图Fig.1 Principle of random drift model

合并各个噪声方程后，随机漂移误差y（t）表达式为

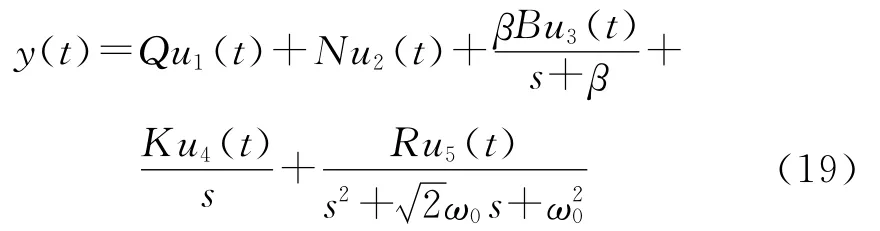
式中：u1（t）到u5（t）表示5组互不相关的单位高斯白噪声；s是微分算子；量化噪声Q、白噪声N、零偏不稳定性B、随机游走K、斜坡误差R取Allan方差计算值；β取4Hz；ω0取0.05rad／s。

3 试验结果

常温下，采集国内某型FOG静态角速率测试数据，采样周期为1s，测试时间为2h，得到随机漂移数据样本如图2所示，其Allan方差分析结果如图3所示。

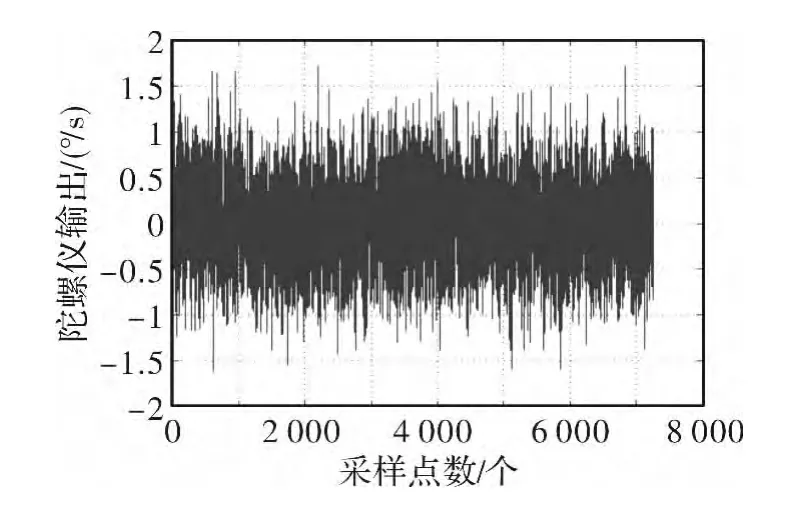
图2 随机漂移数据样本Fig.2 Sample data of random drift

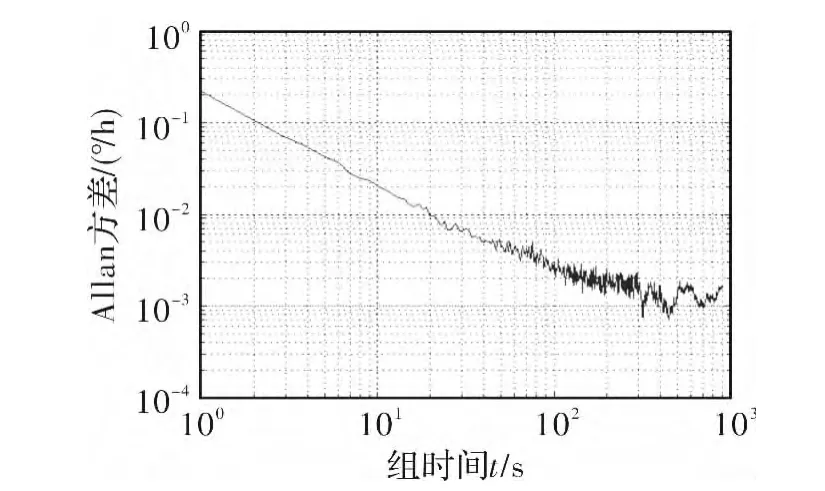
图3 样本数据Allan方差分析结果Fig.3 Analysis result of Allan variance on sample data

用本文所述方法建立随机漂移模型，拟合出的随机漂移误差如图4所示 ，其Allan方差分析结果如图5所示。

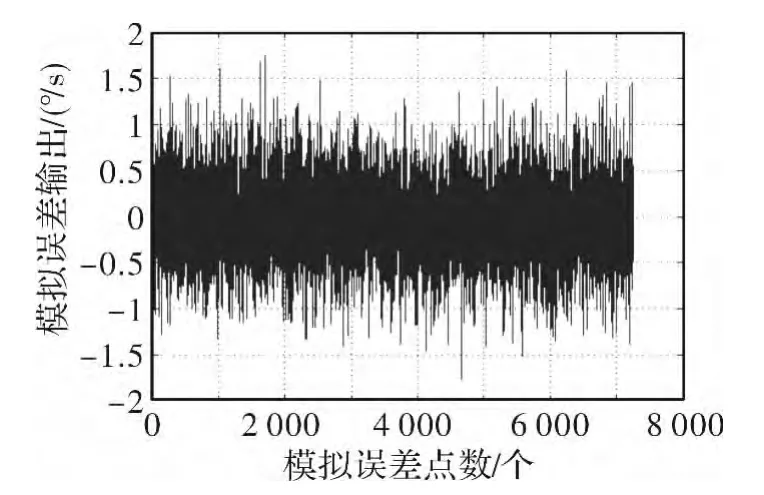
图4 拟合随机漂移数据Fig.4 Fitting data of random drift

图5 拟合数据Allan方差分析结果Fig.5 Analysis result of Allan variance on fitting data

从Allan方差分析图中可看出，样本数据与拟合出的随机漂移在误差特性上基本一致。

取传统FOG随机漂移建模中最常用的时间序列法与分析本文所述方法进行对比分析，具体步骤见文献［10］和文献［11］。对同组样本数据进行预处理后，经适用性检验，选取AR（3）模型建立FOG随机漂移模型，结果如下：

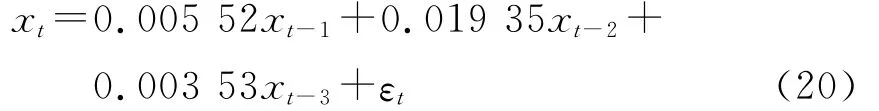
式中：εt～NID（0，σ2）；σ2＝0.207 871。用 Allan方差分析AR（3）模型拟合出的FOG随机漂移，结果如图6所示。

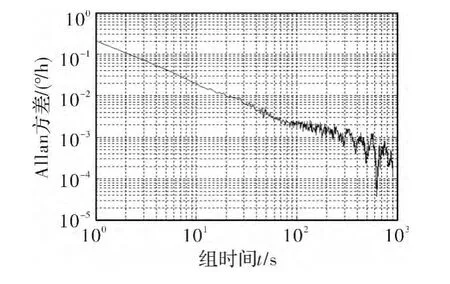
图6 AR（3）拟合数据Allan方差分析结果Fig.6 Analysis result of Allan variance on AR（3）fitting data

用Allan方差所得各项噪声系数对比分析样本数据、AR（3）模型和本文模型拟合出的随机漂移，结果如表1所示。

表1 Allan方差对比分析表Table 1 Comparison and analysis by Allan variance

由表1可知，采用AR（3）模型拟合出的FOG随机漂移，其白噪声和零偏不稳定性较为接近原始数据，但其他噪声项的拟合结果并不理想，单项噪声较原始数据的最大误差为58.3%（斜坡误差）。文中所述方法拟合的FOG随机漂移，其各项噪声项均更加接近原始数据，单项噪声较原始数据的最大误差为8.6%（斜坡误差），远低于传统模型产生的单项噪声误差。

4 结论

在Allan方差辨识系统噪声的基础上，通过各噪声项的功率谱密度函数导出各噪声项的随机微分方程，将辨识出的噪声参数代入各噪声项的随机微分方程，再以单位白噪声驱动各个随机微分方程得到最终误差模型。从仿真结果来看，文中所述模型的拟合精度高于传统模型，是一种有效的FOG随机漂移建模方法。

［1］ 熊 凯，雷拥军，曾海波.基于Allan方差法的光纤陀螺建模与仿真［J］.空间控制技术与应用，2010，36（3）：7-13.XIONG Kai，LEI Yong－jun，ZENG Hai-bo.Modeling and simulation of fiber optic gyros based on Allan variance method［J］.Aerospace Control and Application，2010，36（3）：7-13.（in Chinese with an English abstract）

［2］ BROWN R G，Hwang P Y C.Introduction to random signals and applied Kalman filtering［M］.New York：John Wiley ＆Sons，1997.

［3］ IEEE aerospace and electronic society.IEEE standard specification format guide and test procedure for single-axis interferometric fiber optic gyros［S］.USA：IEEE Press，1997.

［4］ YI Y.On improving the accuracy and reliability of GPS／INS-based direct sensor georeferencing［D］.USA：The Ohio State University，2007.

［5］ 韩松来.GPS和捷联惯导组合导航新方法及系统误差补偿方案研究［D］.长沙：国防科学技术大学，2010.HAN Song-lai.Research on technologies of aeronautic GNSS／SINS integration precision navigation［D］.Changsha：National University of Defence Technolo-gy，2010.（in Chinese）

［6］石国祥，陈坚，叶军.总方差方法在光纤陀螺随机漂移分析中的应用［J］.光电工程，2012，39（1）：63-67.SHI Guo-xiang，CHEN Jian，YE Jun.Applications of total variance method in random error analysis of the fiber optic gyro signal［J］.Opto-Electronic Engineering，2012，39（1）：63-67.（in Chinese with an English abstract）

［7］ ALLAN D W.Statistics of atomic frequency standards［J］.Proceedings of IEEE，1966，54（2）：221-230.

［8］ 祝树生，任建新，张安峰.光纤陀螺随机游走分析方法研究［J］.应用光学，2009，30（6）：1003-1006.ZHU Shu-sheng，REN Jian-xin，ZHANG An-feng.Random walk analysis of fiber optic gyroscope［J］.Journal of Applied Optics，2009，30 （6）：1003-1006.（in Chinese with an English abstract）

［9］ SAVAGE P G.Analytical modeling of sensor quantization in strap-down inertial navigation error equations［J］.Journal of Guidance，Control，and Dynamics，2002，25（5）：833-842.

［10］ 白俊卿，张科，卫育新.光纤陀螺随机漂移建模与分析［J］.中国惯性技术学报，2012，10（5）：621-624.BAI Jun-qing，ZHANG Ke，WEI Yu-xin.Modeling and analysis of fiber optic gyroscope random drifts［J］.Journal of Chinese Inertial Technology，2012，10（5）：621-624.（in Chinese with an English abstract）

［11］ 雷霏霖，刘建伟，吴玉敬，等.机载光电系统中光纤陀螺卡尔曼滤波方法应用［J］.应用光学，2013，34（1）：188-192.LEI Fei-lin，LIU Jian-wei，WU Yu-jing，et al.Application of Kalman filter based fiber optic gyroscope in airborne electro-optical system［J］.Journal of Applied Optics，2013，34（1）：188-192.（in Chinese with an English abstract）