基于组合混沌和位运算的图像加密算法
2014-06-01浩明
浩 明
(西安邮电大学 通信与信息工程学院,陕西 西安710121)
引言
随着网络和多媒体技术的发展和普及,图像等多媒体数据的安全问题日益引起人们的关注。由于数字图像具有冗余度高、数据量大、数据相关性强等特点,采用传统的加密方式进行加密将导致加密速度慢、实时性差等缺点。如何结合数字图像的特点设计有效的数字图像加密算法成为信息安全领域的一个研究热点。混沌系统具有初值敏感性、非周期性、非收敛性、伪随机性等良好的密码学特性,是非线性确定系统。由于内在随机性而产生的外在复杂表现,是一种貌似随机的非随机现象。混沌系统的这些特点使其被广泛应用于数据加密技术[1-7]。当前,基于混沌的数字图像加密方式主要包括基于置乱的加密技术、基于灰度替换的加密技术和基于混合迭代结构的图像加密技术[8-11]。其中基于像素位置置乱的加密算法虽然可以达到对图像加密的目的,但其安全性较差,无法满足实际需求。由于仅通过像素位置置乱加密图像的加密方式存在可恢复周期等安全隐患,研究者进一步提出了将像素位置置乱和灰度替代相结合的加密方式,这种混合迭代结构的加密方式可以有效提高算法的保密性。本文研究了基于混沌和位运算的图像加密算法[12-18],在此基础上,给出了一种改进的基于组合混沌和位运算的图像加密算法,该方法首先对灰度图像进行位平面分解,通过对高四位分别进行置乱变换,再与低四位整体进行置乱变换,然后组合置乱后的位平面,并与二值矩阵进行异或运算得到密文图像。由于在加密过程中结合具有可控放大因子的像素灰度替代加密,能够取得更好的加密效果和安全性。
1 Logistic映射及其特性
1.1 混沌映射
Logistic映射是一种典型的一维混沌系统,其公式定义为

式中:μ为分支参数,0≤μ≤4;k为迭代次数,Xk∈(0,1)。当3.569…≤μ≤4时,Logistic映射处于混沌状态,此时对给定的不同初始条件x0和y0,得到的序列{xk}∞k=0和{yk}∞k=0表现出非周期、非收敛、伪随机等混沌性质。
1.2 基于混沌排序的图像加密算法
设任意明文图像P的大小为M×N,混沌映射的初始条件为μ,x0取正整数t,由(1)式生成混沌序列{xk}k∞=0,从其中第t+1项开始,取其中T项,对取得的序列{Xt+1,Xt+2,…,Xt+T}进行排序得到序列{Xt+1,Xt+2,…,Xt+T},计算序列{Xt+1,Xt+2,…,Xt+T}在原序列{Xt+1,Xt+2,…,Xt+T}中的位置信息,得到对应图像行坐标置乱操作的置乱向量TM={h1,h2,…,hT},实现图像的行置乱。同理可以得到对图像进行列坐标置乱的置乱向量TN,实现对图像的列置乱。通过以上两个过程,实现对图像的位置置乱加密。图1给出了以上方法进行图像加密后的实验结果。
图1的实验结果表明,利用像素级别的图像置乱加密算法,原始图像和密文图像的灰度直方图没有发生改变,说明基于位置置乱的图像加密方式不改变图像的灰度统计信息[19-21],这种特点将使得加密结果不能有效抵抗统计分析攻击。因此,接下来我们给出一种改进的基于混沌和位运算图像加密算法。
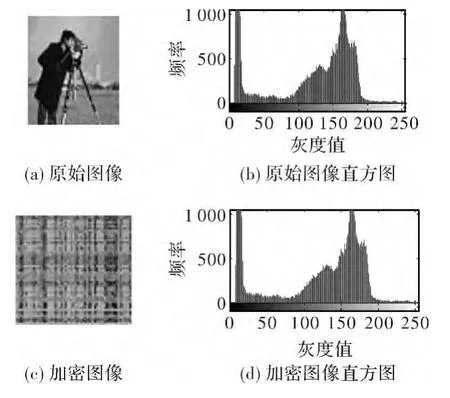
图1 加密效果Fig.1 Effectiveness of encryption
2 算法原理
2.1 基于混沌和位运算图像加密算法
基于混沌和位运算图像加密算法,首先将每个像素分解为bit位,p(i,j)表示原始图像的第i行、第j列的像素值,pt(i,j)表示(i,j)位置像素p(i,j)分解的第t位(t=0,…,7)。由(2)式将一幅灰度图像转换为由0和1组成的二值矩阵:

(3)式可将二值图像恢复成灰度图像:
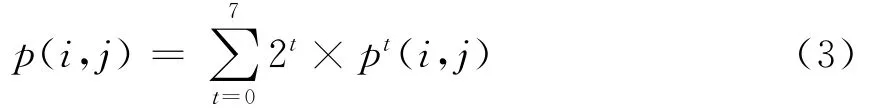
以大小为M ×N 灰度图像为例,由(2)式可转化成大小为M×8 N的二值图像。
该加密过程如下:
Step1:首先读取一幅大小为M×N的灰度图像A。
Step2:由(2)式将图像A转换为M×8 N的二值图像,记为B。
Step3:由(1)式产生混沌序列,按照1.2节的方法,构造行、列置乱向量,置乱图像B,得图像C。
Step4:用(3)式对图像C进行变换,得大小为M×N的密文图像D。
Step5:加密过程结束。
图2给出了应用以上方法进行图像置乱加密的仿真结果。
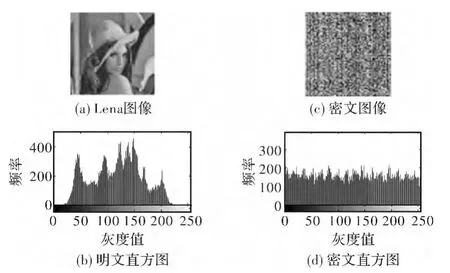
图2 图像置乱加密结果Fig.2 Results of image permutation encryption
图2 的结果表明,基于Logistic和位运算图像加密算法所得密文图像的灰度直方图均匀性较差,加密效果较差,无法保证图像的安全性。因此,本文对该方法进行了改进,采用基于组合混沌和位运算的图像加密算法,取得了良好的加密效果。
2.2 改进算法及其分析
一幅数字图像总可以分解成多个位平面,每个位平面含有不同的图像信息。高位和低位分别代表了数字图像的轮廓和细节,处理不同的位平面相当于对图像不同位置信息进行处理。
一幅m比特灰度级灰度图像,各点像素的灰度值可由下面多项式表示:
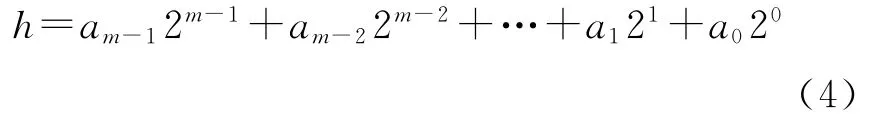
式中:ai表示第i位的取值,ai∈{0,1};2i表示第i位的权重,i=0,1,…,m-1。
对于灰度图像,相同的二进制bit位构成该图像的一个位平面,也就是说同一个bit位的系数集合就是一个二值图像,称作一个位平面。位平面从0开始到m-1共可构成m个位平面,也可将这m个图像组合恢复出原始图像。一个灰度级为256的灰度图像H(x,y),其各像素点的灰度值表示为
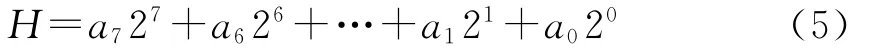
以大小512像素×512像素,256个灰度级的“Lena”图为例。根据像素每位的位置进行分解,图3是分解后的8个二值图像,Pici代表所有像素第i位所组成的二值图像。像素中,每位所包含图像信息量的大小取决于其所在像素的位置,例如,一个像素的第8位的“1”代表128(27),而第1位的“1”代表1(20)。(6)式表示第i位所提供像素p(i)所含图像信息百分比。表1列出不同位平面包含图像信息百分比,尽管p(i)不能完全反应人类肉眼感知的精确百分比信息,但明显看到高位较低位携带更大图像信息,其中i∈[0,7],p(i)计算式为

表1的统计结果表明,灰度图像像素的高四位(第8、7、6、5位)包含了整幅图像信息的94.125%,然而低四位(第4、3、2、1位)仅含不到6%的图像信息。因此,将位平面分为两类,对高四位(Pic8,Pic7,Pic6,Pic5)分别进行置乱,低四位作为整体进行置乱,可以减少加密的执行时间。

表1 不同位像素信息百分比Table 1 Percents of different bit pixel information
改进算法的原理为对每个位平面进行置乱再组合,其像素位置和像素值被同时改变。因此,同时取得了置乱和扩散的双重效果,增强了图像安全性。此外,各个位平面的错误比特分散相互独立,增强其抗攻击能力。将混沌序列应用到该加密算法,产生置乱序列进行图像加密,混沌序列的初始值和参数可以作为密钥。本文加密算法基本思想是:首先对灰度图像进行位平面分解,考虑到图像的高四位含有较大的信息量,因此高四位分别进行置乱,低四位构成一个整体进行置乱,然后组合置乱后的位平面,最后与另一个等大的二值矩阵异或得到密文图像,算法原理如图4,其中位平面的分解和组合公式参考(2)式和(3)式。
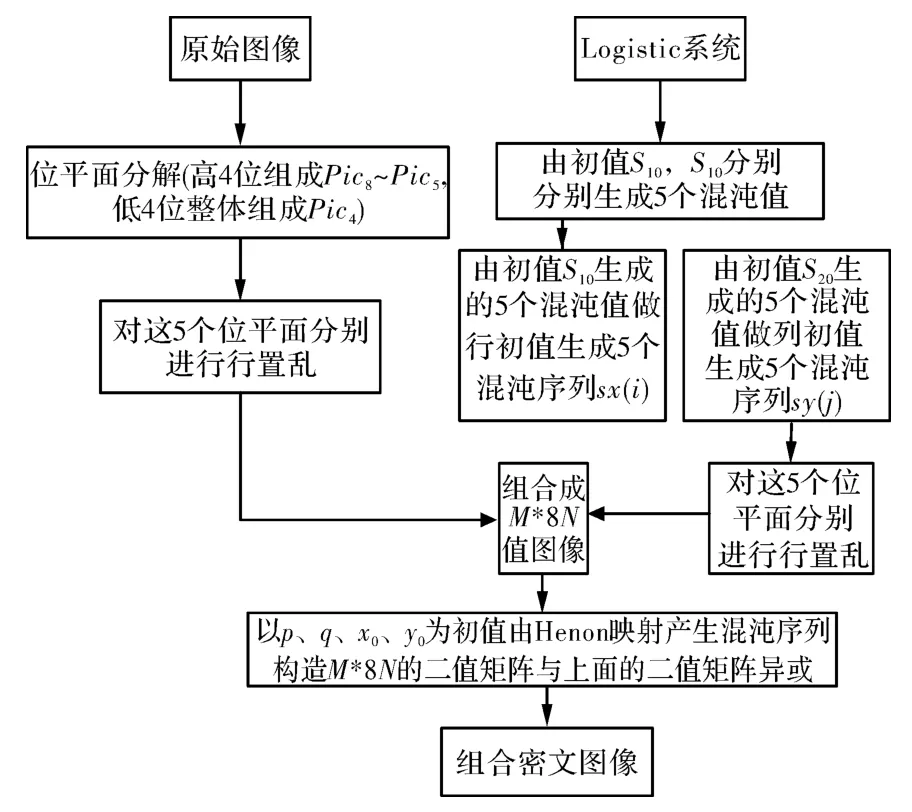
图4 基于组合混沌的位运算图像加密算法Fig.4 Bit operation encryption algorithm based on combined chaos
加密算法流程如下:
Step1:首先读取一幅大小为M×N的灰度图像A。
Step2:对图像A进行位平面分解,获取5个位平面Pic8~Pic4。
Step3:设定初值S10,S20及参数μ,应用(1)式生成两组初始混沌序列S1(m)、S2(m),m=1,2,…,5。
Step4:由step3产生的两组数作初值,再由(1)式生成5组用于行和列置乱混沌序列sx(i),i=1,2,…,M 和sy(j),j=1,2,…,N,其中,M、N分别表示图像的长和宽;
Step5:用step4生成的混沌序列分别对各个位平面进行置乱操作,再组合成M×8 N的二值矩阵B;
Step6:设定初值p、q、x0、y0,由一般的 Henon映射[22]模型
,生成混沌序列构造与B大小相同的二值矩阵C,与B进行异或运算得到图像D。
Step7:将M×8 N的二值矩阵图像D,恢复成M×N的密文图像E。
Step8:加密过程结束。
解密过程与加密过程类似,所需的混沌序列与加密完全相同,对密文图像实施相反的操作,可恢复原始图像。图5为相应的解密流程图。
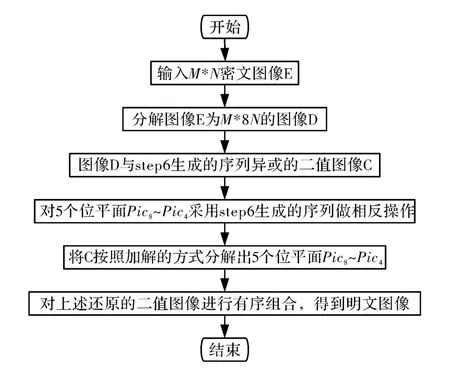
图5 基于组合混沌的位运算图像解密流程图Fig.5 Flow chart of bit operation decryption algorithm based on combined chaos
图6 给出了应用以上图像加密算法的实验结果,图6(b)混沌序列初始条件和参数S10、S20、μ、p、q、x0、y0分 别 为 0.875 6、0.363 5、3.8、1.4、0.3、0.355 4、0.373 5。实验结果表明,明文图像变得面目无存,因此该算法的加密效果良好,保密性高。

图6 置乱加密图比较Fig.6 Comparison of permutation encryption
3 算法分析
3.1 密钥空间分析
本文加密算法在不同阶段分别选取不同的初始条件和参数S10、S20、μ、p、q、x0、y0产生混沌序列,根据IEEE浮点标准[23]可得本节加密算法的密钥为K≈248×248×248×248/2≈2192,因此该加密算法具有巨大的密钥空间,可以有效地抵密钥的穷举攻击,安全性较强。
3.2 密钥敏感性测试
图7(a)和(b)分别是对图6(a)和(c)在μ、p、q、x0、y0不变,S10和S20变换一位的结果(例如:图7(b),S10=0.875 7,S20=0.363 4)。实验结果表明,即使密钥相差10-4,仍解密不出任何原始图像信息,解密图像变得杂乱无章,因此该算法具有良好的抗破解性能,算法保密安全性较好。

图7 密钥敏感性测试Fig.7 Sensitivity testing of key
3.3 直方图测试
以图6为例,图8分别给出原始图像直方图和密文图像直方图对比结果。
图8(b)和(d)表明,原始图像经过2.2节的加密算法加密后,密文图像灰度直方图均匀分布开来,明文图像较高的相关性被扩散到整个密文,每个灰度级的像素非常均匀地分部开,原始图像的统计特性完全被打破,因此该算法具有优良的抗统计分析性能。
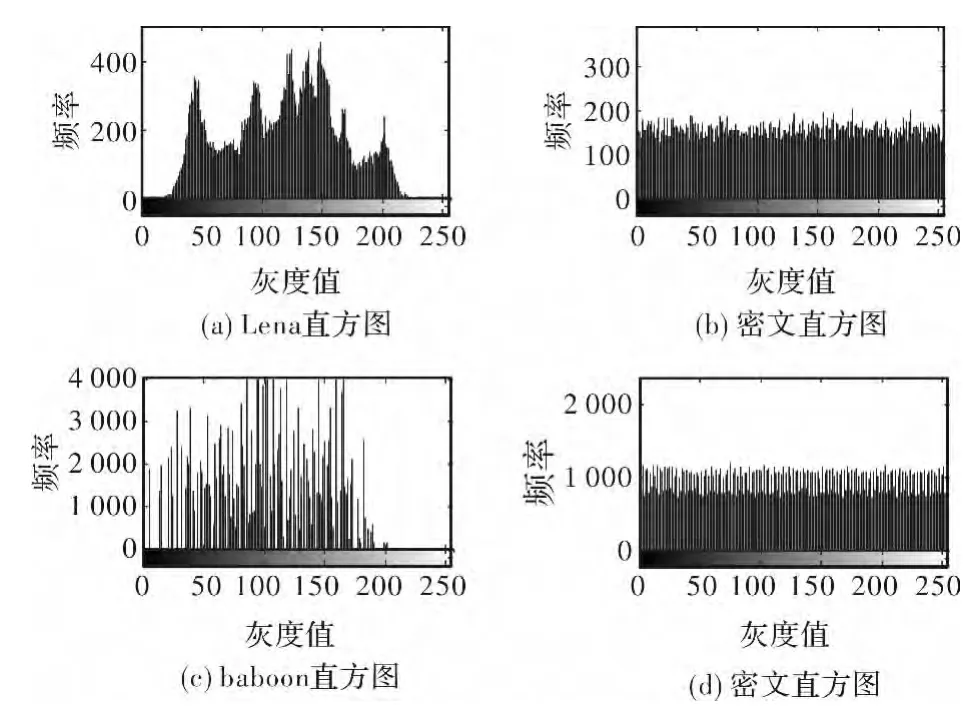
图8 直方图测试Fig.8 Histogram testing
3.4 抗攻击性测试
图9 (a)和(b)分别是对密文叠加强度为0.001的高斯噪声与0.25的椒盐噪声后,通过正确解密流程所得的解密图像。很显然,图像的恢复质量受到噪声影响,但是图像的基本内容仍清晰可见。
图9实验结果表明,在密文图像受到破坏后,仍能较好地解密恢复出原始图像,因此,本算法具有较好抗破坏性。

图9 抗攻击性测试Fig.9 Anti-attack testing
3.5 算法速度测试
由于本文仅对明文分解含有信息量较大的高四bit位平面进行加密,算法执行效率高。表2中给出了本文算法,及像素位置置换算法(PLP)和二维数据加密算法(增强型TDCEA)速度的比较。
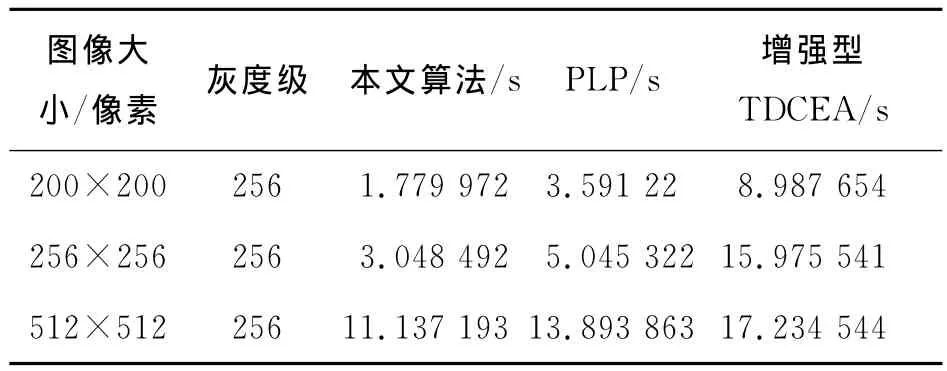
表2 几种加密方法效率比较Table 2 Efficiency comparsion of some encryptionmethods
表2的实验结果表明本文算法对于不同大小的数字图像,加密速度显著高于其他算法,更适合于实时图像加密传输。
4 结论
本文提出了基于组合混沌和位平面的图像加密算法,改进算法结合具有可控放大因子的像素灰度替代加密,能够取得更好的加密效果和安全性。理论分析和仿真结果表明,该算法能实现强大的密钥空间与良好的灰度直方图,具有抗攻击能力高、速度快等优点。
[1] 张小华,刘芳,焦李成.一种基于混沌序列的图象加密技 术 [J].中 国 图 象 图 形 学 报,2003,8(4) :374-378.ZHANG Xiao-hua,LIU Fang,JIAO Li-cheng.An image encryption arithmetic based on chaotic sequences[J].Journal of Image and Graphics,2013,8(4):374-378.(in Chinese with an English abstract)
[2] 叶天语,钮心忻,杨义先.基于奇异值分解和混沌映射的脆弱认证水印[J].光电工程,2008,35(9):138-144.YE Tian-yu,NIU Xin-xin,YANG Yi-xian.Fragile authentication watermark based on singular value decomposition and chaotic mapping[J].Opto-Electronic Engineering,2008,35(9):138-144.(in Chinese with an English abstract)
[3] 赵学峰.基于面包师变换的数字图像置乱[J].西北师范大学学报:自然科学版,2003,39(2):26-29.ZHAO Xue-feng.Digital image scrambling based on the bake's transformation[J].Journal of Northwest Normal University:Natural Science,2003,39(2):26-29.(in Chinese with an English abstract)
[4] 顾勤龙,姚明.基于Logistic混沌序列的数字图像加密研究 [J].计 算 机 工 程 与 应 用,2003,23(3):114-116.GU Qin-long,YAO Ming.A reserch of digital image encryption based on logistic chaotic sequence[J].Computer Engineering and Applications,2003,23(3):114-116.(in Chinese with an English abstract)
[5] 郭建胜,金晨辉.对基于广义猫映射的一个图像加密系统的已知图像攻击[J].通信学报,2005,26(2):131-135.GUO Jian-sheng,JIN Chen-hui. An attack with known image to an image cryptosystem based on general cat map[J].Journal on Communications,2005,26(2):131-135.(in Chinese with an English abstract)
[6] 王让定,李 倩,陈金儿.新颖的音频信息隐藏算法[J].光电工程,2005,32(9):79-82.WANG Rang-ding,LI Qian,CHEN Jin-er.Novel audio information hiding algorithm[J].Opto-Electronic Engineering,2005,32(9):79-82.(in Chinese with an English abstract)
[7] 王云才,马建议,韩晓红,等.混沌激光相关法测距系统的信号采集与处理[J].应用光学,2011,32(3):568-573.WANG Yun-cai,MA Jian-yi,HAN Xiao-hong,et al.Data acquisition and processing of correlation ranging system with chaotic laser[J].Journal of Applied Optics,2011,32(3):568-573.(in Chinese with an English abstract)
[8] 曹建秋,肖华荣,蓝章礼.像素位置与像素值双重置换的混沌加密算法[J].计算机工程与应用,2010,46(28):192-195.CAO Jian-qiu,XIAO Hua-rong,LAN Zhang-li.Chaos encryption algorithm based on dual scrambling of pix-el position and value[J].Computer Engineering and Applications,2010,46(28):192-195.(in Chinese with an English abstract)
[9] WANG Y,WONG K W,LIAO X F,et al.A chaosbased image encryption algorithm with variable control parameters [J].Chaos,Solitons & Fractals,2009,41(4):1773-1783.
[10] 孙鑫,易开祥,孙优贤.基于混沌系统的图像加密算法[J].计算机辅助设计与图形学学报,2002,14(2):136-139.SUN Xin,YI Kai-xiang,SUN You-xian.New image encryption algorithm based on chaos system[J].Journal of Computer-Aided Design & Computer Graphics,2002,14(2):136-139.(in Chinese with an English abstract)
[11] 张健,于晓洋,任洪娥.基于Cat映射和Lu混沌映射的图像加密方案[J].电子器件,2007,30(1):155-157.ZHANG Jian,YU Xiao-yang,REN Hong-e.Image enc-ryption scheme based on Cat map and Lu chaotic map[J].Chinese Journal of Electron Devices,2007,30(1):155-157.(in Chinese with an English abstract)
[12] FU Cong,LIN Bin-bin,MIAO Yu-sheng,et al.A novel chaos based bit-level permutation scheme for digital image encryption[J].Optics Communications,2011,284(23):5415-5423.
[13] YE Guo-dong.Image scrambling encryption algorithm of pixel bit based on chaos map[J].Pattern Recognition Letters,2010,31(5):347-354.
[14] ZHU Zhi-liang,ZHANG Wei,WONG Kwok-wo,et al. A chaos-based symmetric image encryption scheme using a bit-level permutation[J].Information Sciences,2011,181(6):1171-1186.
[15] 张雪锋,范九伦.基于位运算的数字图像隐藏技术[J].信息安全与通信保密,2007(5):149-150.ZHANG Xue-feng,FAN Jiu-lun.An image hiding method based on bit-operation[J].Information Security and Communications Privacy,2007(5):149-150.(in Chinese with an English abstract)
[16] 许艳.基于位运算的BMP图像加密算法研究[J].湖南理工学院学报:自然科学版,2007,20(4):41-43.XU Yan.Research of BMP image encryption algorithm based on bit operation[J].Journal of Hunan Institute of Science and Technology:Natural Sciences,2007,20(4):41-43.(in Chinese with an English abstract)
[17] 袁玲,康宝生.基于Logistic混沌序列和位交换的图像置乱算法[J].计算机应用,2009,29(10):2681-2683.YUAN Ling,KANG Bao-sheng.Image scrambling algorithm based on Logistic chaotic sequence and bit exchange[J].Journal of Computer Applications,2009,29(10):2681-2683.(in Chinese with an English abstract)
[18] 李涛,柳健.基于位平面与混沌系统的图像置乱方法[J].西南民族大学学报:自然科学版,2008,34(3):595-599.LI Tao,LIU Jian.Image scrambling based on bitplane decomposition and chaotic system[J].Journal of Southwest University for Nationalities:Natural Science Edition,2008,34(3):595-599.(in Chinese with an English abstract)
[19] 张琼,沈民奋,翟懿奎.基于三维混沌猫映射的图像加密 算法的改进[J].系统工程与电子技术,2007,29(9):1568-1572.ZHANG Qiong ,SHEN Min-fen,ZHAI Yi-kui.Improving image encryption method based on threedimensional chaotic cat map[J].Systems Engineering and Electronics,2007,29(9):1568-1572.(in Chinese with an English abstract)
[20] 王珊珊,陈艳峰.一种基于混沌的图像加密算法[J].微计算机信息,2009,25(3-3):62-63.WANG Shan-shan,CHEN Yan-feng.An algorithm of image encryption based on chaos[J].Microcomputer Information ,2009,25(3-3):62-63.(in Chinese with an English abstract)
[21] RHOUMA R,BELGHITH S.Cryptanalysis of a new image encryption algorithm based on hyper-chaos[J].Physics Letters A,2008,372(38):5973-5978.
[22] 黄大足,陈志刚,朱从旭.基于广义猫映射与神经网络的图像空域水印算法[J].计算机应用研究,2008,25(4):1144-1146.HUANG Da-zu,CHEN Zhi-gang,ZHU Cong-xu.Image spatial domain watermark algorithm based on general Arnold mapping and neural network[J].Application Research of Computers,2008,25(4):1144-1146.(in Chinese with an English abstract)
[23] KAHAN W.IEEE standard 754for binary floatingpoint arithmetic[S/OL].(2001-08-06)[2012-1-1].http://www.cs.berkeley.edu/~wkahan/ieee754status/IEEE.
