飞机道面EMAS阻滞性能建模分析

于鸿彬，赵合欢，曹立志

（1.天津工业大学机械工程学院，天津 300387；2.天津大学 管理与经济学部，天津 300072）

飞机道面EMAS阻滞性能建模分析

于鸿彬1，赵合欢1，曹立志3

（1.天津工业大学机械工程学院，天津 300387；2.天津大学 管理与经济学部，天津 300072）

结合实际情况，对机轮作用下EMAS的破坏作用做了静力学分析.在此基础上，对系统作了适当的假设和简化，建立了含有耗散函数的Lagrange动力学方程.此外，运用MATLAB软件对该动力学模型进行了仿真，得到了飞机在X、Y方向上位移和速度随时间变化的曲线，较好地描述了真机在EMAS阻滞状态下的实际情况，验证了该系统模型的有效性,为飞机道面EMAS的进一步研究提供了有效的理论支持.

飞机道面；EMAS；阻滞性能；静力分析；动力学模型；仿真

随着社会的发展，空中交通日益增多，由于气象因素、机械事故、驾驶员操作失误等原因，飞机冲出跑道的事故也随之增多.如何有效地减小飞机在发生冲出跑道事故时所遭受的危害，进而保障机上人员的生命安全，减小对飞机机身的损伤，现己成为当前世界各个机场所迫切需要解决的问题.目前国内外使用较多的是液压形式的拦阻系统，液压系统沿跑道对称布置并横跨跑道两端的钢缆或拦阻网，将飞机本身的动能转化成液压能从而达到拦阻飞机的效果.这类拦阻系统结构复杂，具有很多不足之处[1].目前，由美国ESCO公司和FAA共同研制的工程材料阻滞系统（engineered materials arresting system，EMAS）已成为阻滞飞机越界的专用设备[2].EMAS的阻滞材料研发[3]、数学模型研究[4]和阻滞区结构设计等关键技术在美国已比较成熟，并且该系统在美国已得到较为广泛的应用[5]，在实际使用中发挥了重要作用.而中国目前尚处于起步阶段，相关研究亟待开展.相对于液压式拦阻系统，EMAS不需要复杂的机械结构，可靠性高，易于实现并且能够节约土地资源，在中国有广阔的发展空间和应用前景.本文根据机轮与拦阻材料的交互模型，给出详细的机轮受力的表达式.最后合理简化飞机模型，建立拦阻系统的动力学模型.

1 飞机拦阻系统数学模型的建立

1.1 机轮与拦阻材料作用机理

为了确定拦阻材料的拦阻性能，本文建立了机轮与泡沫混凝土的交互模型.该交互模型是飞机阻滞系统的动态模型，在飞机压过EMAS时，它能够计算出泡沫混凝土作用于机轮的动载荷.对于EMAS中一个给定的运动方向的机轮，设FD为拦阻材料作用于单个起落架机轮的水平方向的总阻力，也就是使飞机减速的力.FC为拦阻材料作用于机轮的垂直方向的力，即支撑飞机的力.机轮所受水平方向的阻力由4部分构成，包括泡沫混凝土动态压实阻力FD1、撕裂力FD2、粘附阻力FD3以及等效的摩擦力FD4.

1.1.1 动态压实阻力

当飞机越界进入泡沫混凝土时，机轮陷入拦阻材料并产生一条有一定深度和宽度的机轮印迹.机轮和泡沫混凝土之间的截面被分为2个部分，即弧段部分和压实部分，如图1所示.

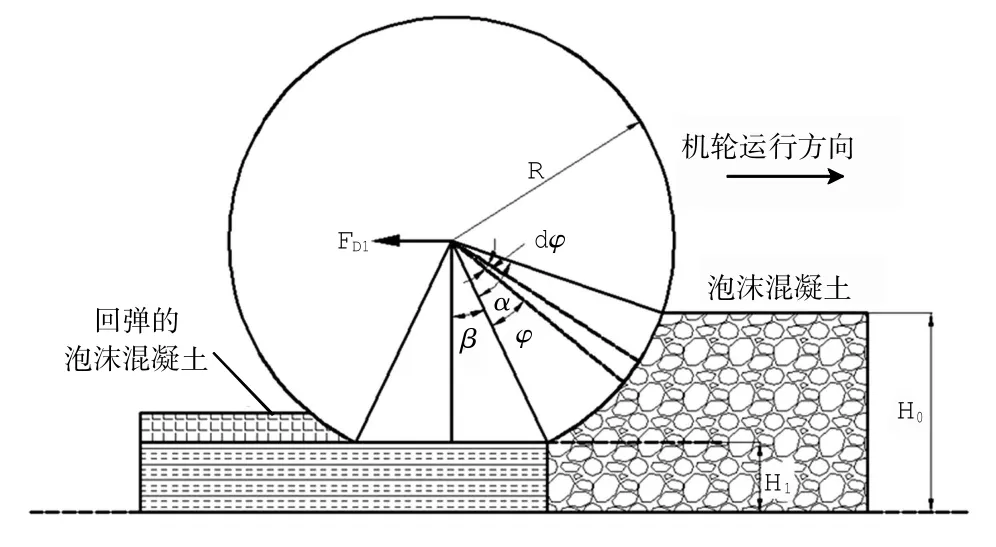
图1 机轮与泡沫混凝土交互模型简图Fig.1 Schematic of interaction between an aircraft tire and foamed concrete

图中：H0为泡沫混凝土的初始高度；H1被压实的泡沫混凝土高度；R为机轮半径.图中还定义了角β，计算方式如下：

式中：Mx为飞机机轮承受的重量；g为重力加速度；PL为胎压；B为机轮宽度.根据材料压缩的强度条件，在角度φ增量dφ上机轮所受的水平阻力为：

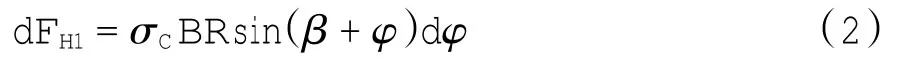
式中φ从0到α积分，可以得到机轮在水平方向上所受到的水平压实阻力：

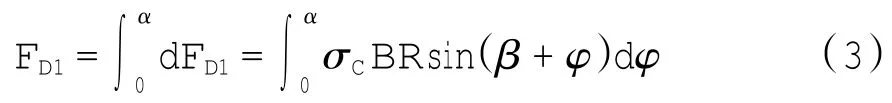
根据泡沫混凝土的力学特性，假定泡沫混凝土的应力应变模型服从幂律模型[6]，则应力σ有以下关系：

式中：ε为泡沫混凝土的压缩应变；σ0为泡沫混凝土初始屈服应力；k、n为与材料力学性能有关的参数.

假定机轮与泡沫混凝土之间无相对滑动，根据图2可知，压缩应变ε包括竖直方向的应变ε1和水平方向的应变ε2，则根据图中几何关系可知：

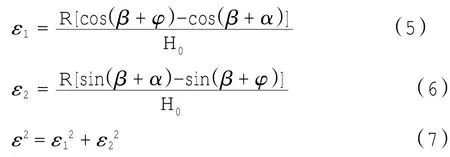
将式（5）和（6）带入（7）中，可得泡沫混凝土的压缩应变为：

将式（4）和（8）带入（3）中，可得拦阻材料的水平方向压实阻力：

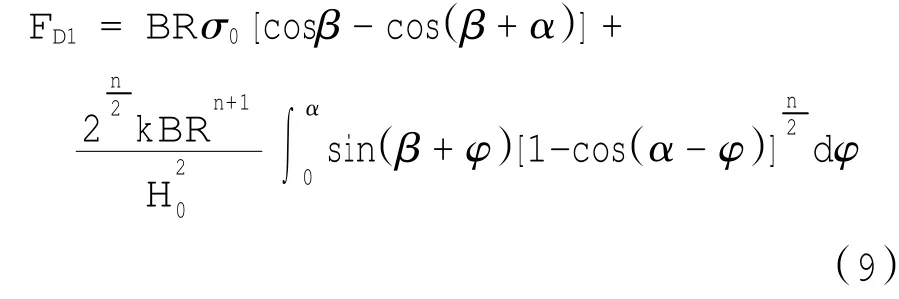
1.1.2 泡沫混凝土撕裂力

当机轮压过泡沫混凝土时，它会撕裂机轮两侧的泡沫混凝土，设在水平方向的撕裂力为FD2，根据图1中的几何关系，可得撕裂力的表达式[7]：

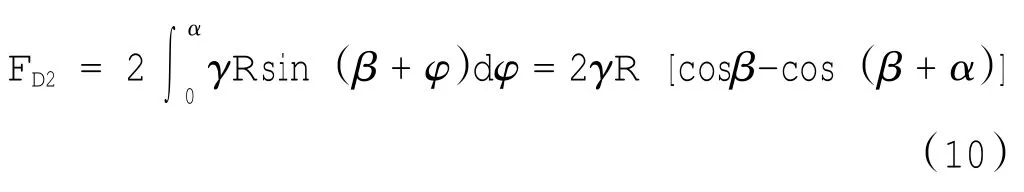
式中：γ为单位面积的撕裂阻力.

1.1.3 泡沫混凝土粘附阻力

当机轮在泡沫混凝土中滚动时，由于惯性作用，轮胎下的混凝土会随着轮胎面运动而产生阻力，即粘附阻力FD3.在该过程中，飞机的一部分动能会转化为机轮下混凝土的动能，且混凝土的速度与机轮表面对应点的速度大小以及方向应该是相等的，如图2所示.

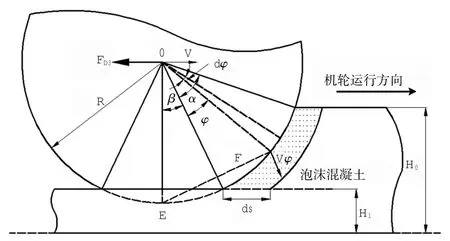
图2 纯滚动状态下机轮受粘附阻力细部图Fig.2 Adhesive resistance of tire under pure rolling condition

由于机轮做纯滚动，因而机轮与泡沫混凝土的虚拟接触点E点速度为0，设机轮在水平方向上的速度为V，根据图中的几何关系，可得到方向如图所示的Vφ，计算得：

当机轮向前移动一微段ds时，可以得到该微段泡沫混凝土的动能dT，即：

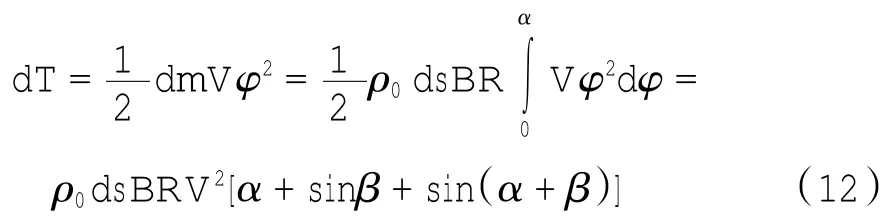
式中：ρ0为泡沫混凝土的初始密度.

在该微段粘附阻力所做的功为FD3·ds，而该段泡沫混凝土的动能恰好等于粘附阻力所做的功，即：

消去等式两侧ds，则可得粘滞阻力FD3为：

1.1.4 等效摩擦力

为了确保飞机能够不断减速停止在跑道安全区域内，轮胎面和跑道之间的摩擦力应满足文献[8]所述.当机轮进入EMAS后，机轮与混凝土之间的会产生2部分摩擦力:一部分是轮胎面与压缩的泡沫混凝土之间的摩擦;另一部分为机轮两侧面与混凝土断面之间的摩擦.由于侧面压力很小，因而侧面摩擦可忽略不计.机轮与泡沫混凝土之间的摩擦力可以简化为：

式中：FC为泡沫混凝土对机轮垂直方向的支持力.

综上可得，单个机轮受到泡沫混凝土的总阻力为：

由于飞机的前起落架和主起落架均有2个轮子，这对于前起落架来说，有如下关系：

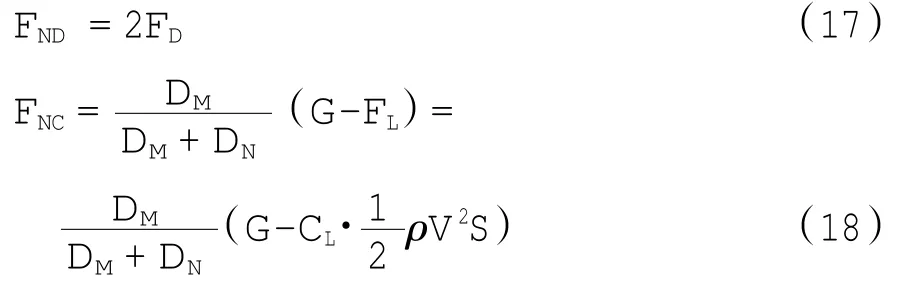
式中:FND和FNC分别为前起落架的总阻力和总支持力；μ为等效摩擦系数；G为飞机重力；FL为升力；CL为升力系数；ρ为空气密度；V为飞机速度；S为机翼面积；DM为主起落架到重心的距离；DN为前起落架到重心的距离.对于每个主起落架也有同样的关系式，即：

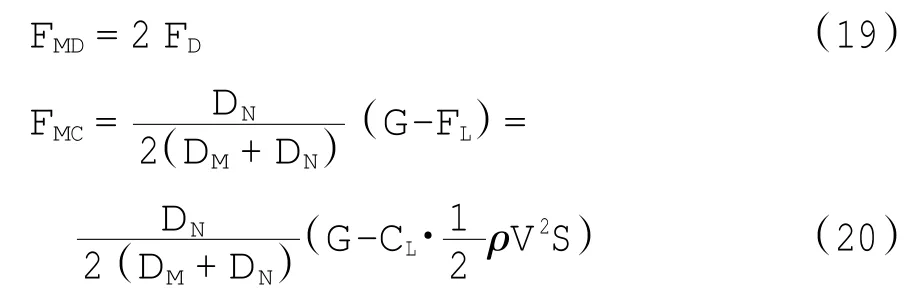
1.2 建立系统的动力学方程

飞机进入EMAS是一个非常复杂的过程，为了得到系统的动力学模型，如图3所示.我们进行以下假设和简化：飞机为理想刚体，弹性形变可忽略不计；飞机为二维运动，即只在竖直平面内运动，不存在侧向滑动；机身倾斜角度θ为小量，小于±10°；将起落架简化为弹簧阻尼器，前起落架弹簧的弹性系数为KN，阻尼系数为CN,主起落架弹簧的弹性系数为KM，阻尼系数为CM.

图3 飞机动力学模型Fig.3 Aircraft dynamic model

仅考虑飞机的平面运动，选取飞机水平位移x，竖直位移y，机身俯仰角θ，3个独立坐标，利用Lagrange[9]方法建立系统动力学方程，包括机身在水平和竖直方向的动力学方程以及机身俯仰轴动态力学平衡方程.

1.2.1 系统动能

系统的动能包括飞机平动和绕质心转动的动能，即：

1.2.2 系统势能

系统的势能包括重力势能和弹性势能2部分.首先求出飞机弹簧阻尼器的压缩量，令yM表示主起落架弹簧阻尼器的压缩量，yN表示前起落架弹簧阻尼器的压缩量，而压缩量包括静平衡状态的压缩量和动平衡状态的压缩量，则前、主起落架的压缩量分别为：

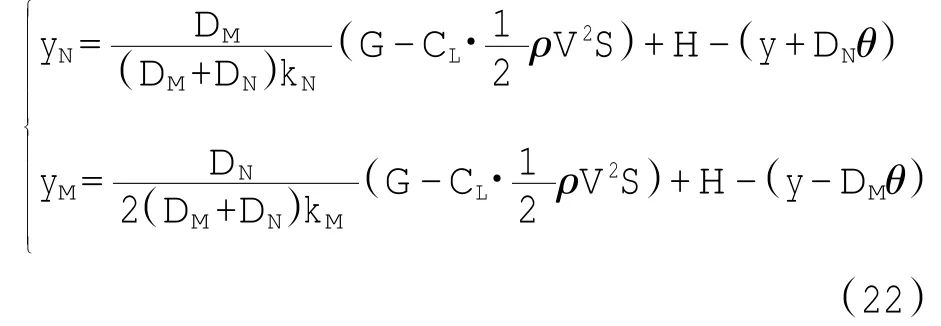
因而可得系统的总势能为

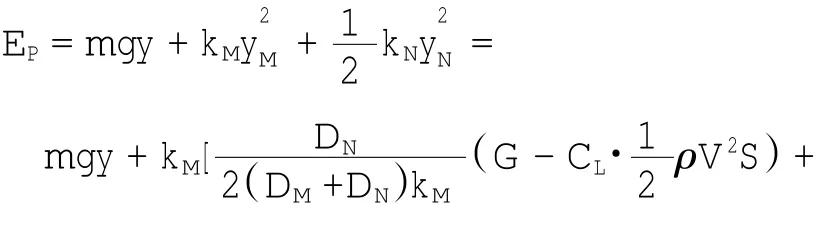
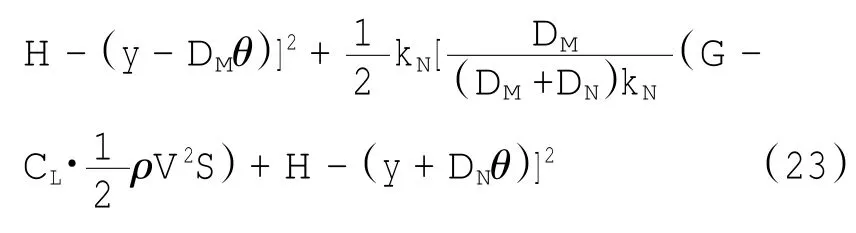
1.2.3 系统的Rayleigh耗散函数

将起落架简化为弹簧阻尼器，那么系统内必定存在粘性摩擦，将所需要的变量带入耗散函数ψ=可得系统的耗散函数为：

1.2.4 系统动力学方程

含有耗散函数的Lagrange方程如下：

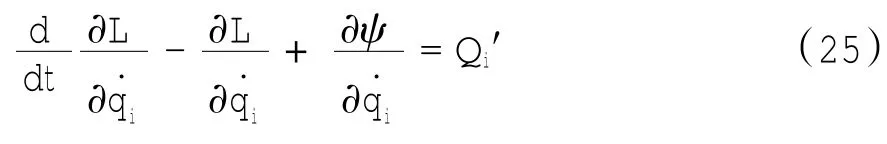
式中：qi为广义速度；Qi′为广义耗散力；L=EK+EP.将系统的动能EK和系统的势能EP以及耗散函数ψ带入上式，可得到系统动力学方程，即：

2 动力学模型仿真结果及分析

对于本动力学模型，采用MATLAB求解微分方程的ode45()模块求解，该模块具有强大数值计算能力，ode45()采用的是变步长四阶五级的Runge-Kutta算法，用ode45()模块可求出x、y、θ、x˙、y˙、θ˙的数值解，再描绘出x、y、θ、x˙、y˙、θ˙随时间t变化的曲线，这样可以对系统的动力学特性有一个更直观的了解.

本仿真参数为B747-400F参数，拦阻材料简化为高度相同的泡沫混凝土，设飞机进入拦阻道面的速率为40 km/h，图4为X方向的位移曲线，可以看出，飞机停止距离约为145 m，拦停时间约为7.2 s，距离过渡均匀.图5为X方向的速度曲线，可以看出前期速度有较大波动，后期速度变化趋于线性变化，符合预期要求.对于图6中Y方向的位移曲线，呈现出有规律的波动性变化，可以看出前期位移变化稍大，中期波动变小，而后期又有稍微大的波动，这种情况符合实际中拦阻飞机过程的运动规律.图7的速度曲线与位移曲线的变化相吻合.对于乘客来说，短期内X方向速度变化很大，承受的主要是X方向的载荷.

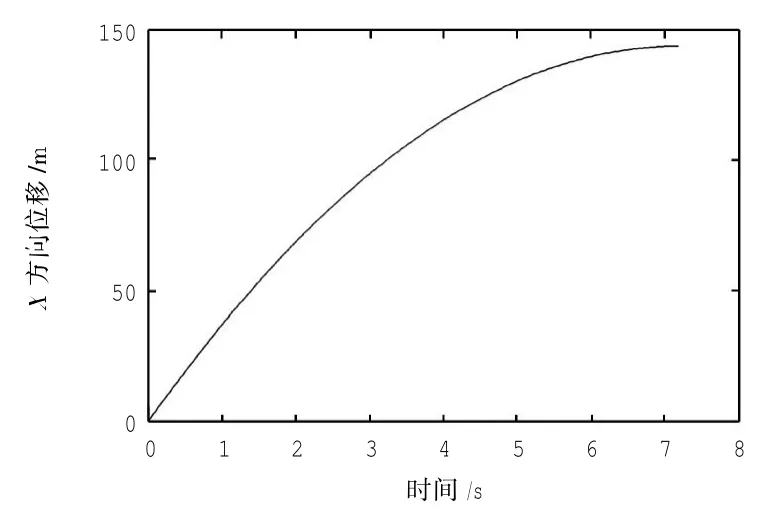
图4 X方向位移曲线Fig.4 Displacement curve of X direction

图5 X方向速度曲线Fig.5 Speed curve of X direction

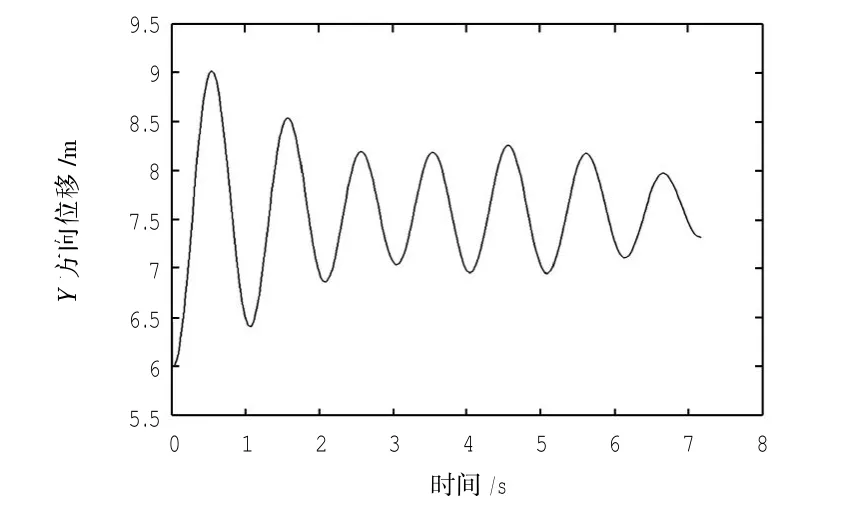
图6 Y方向位移曲线Fig.6 Displacement curve of Y direction

通过该仿真，得出以下结论：

（1）从仿真结果看出，建立的数学模型能够较好地描述整个拦阻过程的位移和速度变化，此外，还可以进一步对本仿真的参数进行改进并优化拦阻模型，以此降低真机试验的次数，减少不必要的试验损失.

（2）本系统的动力学模型仿真结果验证了飞机道面EMAS的有效性和可靠性，能够给予以后的机场拦阻设施的铺设提供有效的理论依据.

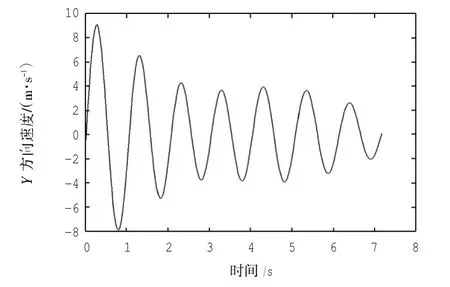
图7 Y方向速度曲线Fig.7 Speed curve of Y direction

3 结束语

本文通过建立飞机道面工程材料阻滞系统的静力学和动力学分析模型，得到了飞机前起落架和主起落架所受到的阻滞力以及支持力，同时还得到了对拦阻飞机起主要作用的动态压实阻力与泡沫混凝土的材料密度的数学函数关系式，并对压溃情况的瞬态进行了合理的假设分析.文中还对飞机模型进行了合理的简化，建立了系统的动力学方程.最后，利用MATLAB对动力学模型进行动力学仿真来验证方程和合理性和有效性.本文可以为以后拦阻材料的密度、高度、大小等因素的确定以及真实的试验仿真给出理论支持.

[1]柳钢，聂宏.基于能量法的飞机拦阻动力学分析[J].中国机械工程，2009，20（4）：450-454.

[2] ICAO.Status Engineered Material Arresting System Installations in the United States[C]//Apresentation by the North American，Central American and Caribbean Directors of Civil Aviation，2006.

[3] SUITS L David，SPRINKLE Michael M，DIETZ Arlene L，et al.Control of cracking In concrete：State of the art,E-C107 [R].Transportation Research Board of the National Academies, 2006.

[4] RAGSDALE W A.A generic landing gear dynamics model for LASRS++[C]//AIAA Modeling and Simulation Technologies Conference.2000：1-9.

[5]HEYMSFIELD E，HALE W M，HALSEY T L.A parametric sensitivity analysis of soft ground arrestor systems[J].ASCE, 2007，262（20）：227-236.

[6]PATTOFATTOS，ELNASRII，ZHAOH，etal.Shock enhancement of cellular structures under impact loading[J].Journal of the Mechanics and Physics of Solids，2007，12（55）：267-286.

[7] ZHANG Z Q，YANG J L.An analytical model of foamed concrete aircraft arresting system[J].International Journal of Impact Engineering，2013，61：1-12.

[8]HEYMSFIELDE，HALE WM，HALSEYTL.Aircraftresponse in an airfield arrestor System during an overrun[J].Journal of Transportation Engineering，2012，138（3）：284-292.

[9]符瑞生.拉格朗日方程的形式[J].河南大学学报，1986（4）：79-83.

Modeling and analysis of arresting property of EMAS for aircraft-pavement

YU Hong-bin1，ZHAO He-huan1，CAO Li-zhi2
（1.School of Mechanical Engineering,Tianjin Polytechnic University,Tianjin 300387，China；2.College of Management and Economics,Tianjin University,Tianjin 300072,China）

Combining with actual situation,the statics analysis under the action of the wheel of EMAS is made.On this basis, the system makes reasonable assumption and simplification,and establishes dynamics equations of Lagrange contains dissipative function.In addition,using the MATLAB to simulate the dynamic model,the system obtains the curve changes with the time of the X,Y direction of the plane,and describes the actual situation of the plane in the arresting condition of EMAS,and verifies the effectiveness of the model,which provides effective theoretical support for further research of EMAS of aircraft-pavement.

aircraft-pavement；EMAS；arresting property；static analysis；dynamic model；simulation

O313；V351.11

A

1671-024X（2014）05-0084-05

2014-05-05

国家自然科学基金民航联合研究基金（U1333129）

于鸿彬（1974—），男，副教授，硕士生导师.E-mail：350420028@qq.com