一种使用灰度预测模型的强自适应性移动节点定位算法

单志龙 刘兰辉 张迎胜 黄广雄



一种使用灰度预测模型的强自适应性移动节点定位算法

单志龙 刘兰辉*张迎胜 黄广雄

(华南师范大学计算机学院 广州 510631)

定位技术是无线传感器网络的关键技术，而关于移动节点的定位又是其中的技术难点。该文针对移动节点定位问题提出基于灰度预测模型的强自适应性移动节点定位算法(GPLA)。算法在基于蒙特卡罗定位思想的基础上，利用灰度预测模型进行运动预测，精确采样区域，用估计距离进行滤波，提高采样粒子的有效性，通过限制性的线性交叉操作来生成新粒子，从而加快样本生成，减少采样次数，提高算法效率。仿真实验中，该算法在通信半径、锚节点密度、样本大小等条件变化的情况下，表现出较好的性能与较强的自适应性。

无线传感网络；定位；移动节点；灰度预测

1 引言

集成了传感器、微机电系统和网络3大技术的无线传感器网络(WSN)是一种全新的信息获取和处理技术[1]，它由大量部署在监控区域的传感器节点组成，通过无线通信方式形成一个多跳自组织网络系统，协作感知、采集和处理相关监控信息。WSNs 技术被众多重要组织和机构预测为可以改变世界的核心科技力量[2]，其中定位技术[3]是无线传感器网络的关键支撑技术。无线传感器网络定位算法主要分为测距算法和非测距算法两大类。测距算法依赖额外硬件测量节点间的距离信息，如接收信号强度(RSSI)[4]，信号的角度差(AOA)[5]，信号到达时间差(TDOA)[6]等；非测距算法主要根据节点的连通性实现节点定位，定位成本较低，例如质心算法[7]，APIT算法[8]，DV-Hop算法[9]，MDS-MAP算法[10]等。

上述定位算法在静态网络中有较好的效果，但在移动定位中则表现不佳，目前移动定位应用最广泛的是GPS[11]定位，但在WSNs中给传感器节点配置GPS模块由于价格耗费问题使其并不实际，设计更有效的移动节点定位算法也成为一个热点研究问题。Hu等人[12]基于蒙特卡罗算法随机化采样的思想提出了适用于移动传感器网络节点定位跟踪的MCL(Monte Carlo Localization)算法，提供了一种很好的研究思路。在此算法的基础上，李敏等人[13]提出了一种MCLAS算法：采样时通过参考节点选择模型，选取离定位节点较近且分布均匀的参考节点构成采样盒，并利用权重来进行位置估计，提高定位精度。王洁等人[14]提出减少采样区域提高MCL算法的样本质量，同时用遗传交叉的思想加快生成样本。刘志华等人[15]提出根据运动的连续性，利用最小二乘曲线拟合的方法，推算出未知节点下一时刻可能的位置区域，进行快速抽样和样本过滤。朱海平等人[16]提出通过构建接收信号强度指示测距模型来限制样本区域以提高采样效率。

本文提出的使用灰度预测模型的强自适应性移动节点定位算法(strong self-adaptive Localization Algorithm based on Gray Prediction model for mobile node, GPLA)在基于MCL的思想上提出了不同的解决方案：首先，为确定更加精准的采样区域，减少重复采样计算量，本文通过记录待定位节点前几个时刻的位置信息利用灰度预测模型估算出当前的运动速度和方向，确定大致运动区域，精确采样空间。然后，使用锚节点与定位节点之间的估计距离信息来滤除粒子，提高粒子质量和有效性，从而提高定位精度。最后利用限制性的线性交叉来扩展粒子数目，通过粒子团防止采样收敛，形成采样粒子的多样性，在减少采样时间的同时，加快高质量样本生成，达到更快，更准确的定位。

2 MCL算法分析

蒙特卡罗定位算法的核心思想是：在贝叶斯滤波位置估计的基础上，把待定节点可能出现的位置用加权样本集的形式表示，用个带有权重的离散采样来估计节点位置。主要通过预测阶段和滤波阶段实现节点定位。

与其它定位算法相比，蒙特卡罗方法具有其特性：MCL定位算法计算简单，复杂性低。定位过程中的收敛速度和粒子采样对定位环境依赖性低。算法随机性强，适合解决节点运动的无规律问题。定位精度受节点移动性影响不大，而定位过程中充分利用了节点移动特性和与其它节点的连通特性。能够在节点存储空间非常有限、锚节点分布密度较低的情况下实现移动节点的定位。这些特性使MCL算法思想很适合应用到节点移动定位中，具有较大的发展潜力。在经过不断的研究后，会更大程度地提高节点定位精度。

3 GPLA算法

GPLA算法通过灰度预测模型预测未知节点的运动状况，提高采样的准确性，通过估计距离进行滤波增加定位精度，在限制性的线性交叉操作下，生成有效性粒子，减少采样次数，整个算法环环相扣，具有较强的自适应性，在提高定位精度的同时减少定位时间。

3.1 运动预测模型

传感器节点的移动过程大多数情况下都是与前面几个时刻的位置有关联的，在某种程度上可以看作是基于时间序列短暂连续的。假设节点的运动平滑、连续，则可以借助前面几个时刻的位置信息预测当前时刻的运动状况。灰色预测[17]通过鉴别因素之间发展趋势的相异程度，对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势。它可以解决信息贫乏的不确定性、随机性强问题，且对环境因素的依赖性较小，这非常适合移动节点定位时的时序性和随机性，且只需要记录前面几个时刻的数据信息，再通过微分方程模型来预测当前时刻数据，这样不会增加节点负载和计算量。

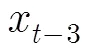
(1)通过历史记录信息，对数据累加构造累加生成序列：

(2)构造数据矩阵和数据向量：

(3)计算参数：

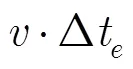
符合上述条件的采样集合可描述为

3.2 滤波加权阶段

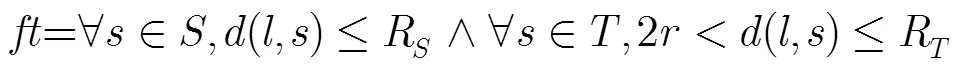
在时刻，预测位置也必然会处于它侦听到的所有锚节点估计距离范围内，如果不在该相交区域，则该采样点不符合条件，要去除掉。如果采样粒子不在上述区域，分布概率()0，在区域则为1，分布概率则表述为

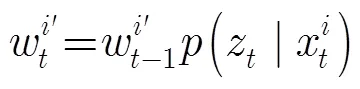
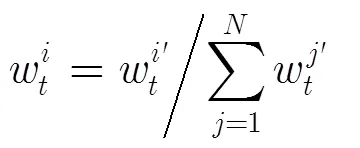
3.3 限制性线性交叉

当满足滤波条件的采样粒子达到一定数目(/4~/2)后进行限制性线性交叉操作：在通过滤波条件的采样粒子群内选取粒子对，并在其内部连线上按交叉因子产生新的粒子，新粒子必然位于粒子对之间，也必定是符合滤波条件的，就不再需要重新滤波验证，这样在加快样本生成的同时，也减少了计算量，另外，为了避免采样局部化，通过划分粒子团来限制粒子对的生成次数，由同一粒子和其产生的新粒子视为一个团，以此来限制多次交叉后粒子弱化。具体操作如下：

在满足滤波条件的粒子集合中选取权值较高的一部分作为初始集群，从中随机选择两个粒子进行线性交叉操作：

其中(x,y), (x,y)为样本粒子坐标，为交叉因子，取值范围为[0.2,0.8], (x,y)为新粒子坐标。

采用线性交叉时，同一对粒子与它们交叉生成的新粒子归为一个粒子团，团内进行2~3次交叉后将不再进行交叉，即团内最多只能生成3个新粒子，然后再与其它团的粒子组成新粒子对进行交叉操作。这样可以减缓交叉的收敛速度，保持样本的多样性。如图2所示，圆点表示采样粒子，四角形表示节点真实位置，三角形是遗传交叉新生成的粒子，椭圆形内是团，团与团之间可以进行交叉，经过限制性线性交叉方法生成的粒子都是符合滤波条件的，不用再进行验证操作。限制性线性交叉方式使样本生成不再容易收敛，同时能保持粒子的多样性，快速生成样本集，大幅度地降低算法的运算时间和复杂度。

3.4 节点位置、误差计算

最后统计的样本数如果还是不足，就需要重复从预测阶段开始，将角度扩大一倍在新区域重新采样并执行后续操作，反复直至达到样本点的数目。此时，可计算出移动节点在时刻的位置：

节点位置误差计算公式为

其中，表示节点通信半径，(x,y)表示当前时刻的估计位置，(,)表示粒子的实际位置。er越小则估计位置越精确。

4 仿真分析

算法的实验仿真在MATLAB平台下进行，并同原始MCL算法和EMCL[13]算法进行了比较。仿真区域设置为250 m×250 m，节点移动模型采用随机waypoint模型，锚节点的移动速度在[0~5 m/s]之间随机选取。默认条件的仿真参数为：节点总数CN=250，锚节点数CA=50，通信半径=35 m，未知节点最大速度max=10 m/s，样本=25。未知节点在移动的过程中取20个时间周期进行定位，重复运行20次后，取平均获得仿真结果。

在移动节点定位中，通信半径是对定位精度影响比较大的因素。如图3所示，随着半径的增大，3种算法的定位误差都在减小，因为节点通信半径增大，获得的观测信息也增多，能够排除一些非有效性的粒子。在半径达到45 m之后，定位精度开始稳定，在整个过程中，GPLA算法的定位误差比另两种算法要低，这是因为它充分利用了观测信息和历史位置信息，在灰度预测后的预测区域采样，用估计距离信息代替通信半径范围信息进行滤波，能够更进一步提高粒子的有效性，因而其定位精度优于另两种算法。

当锚节点数变化时未知节点得到的观测信息也会发生变化，进而会影响滤波环节得到的采样粒子的好坏程度，从图4可看出，当锚节点数较少时，GPLA算法和EMCL算法的定位误差相差不大，因为锚节点太少时能获得的观测信息会减少，在这种情况下，用通信半径和用估计距离信息进行滤波效果相当，当锚节点增加时，两种滤波方法的区别就比较明显了，GPLA算法中未知节点根据与锚节点的估计距离进行滤波，粒子的有效性增加，估计位置就越接近未知节点的真实位置。

在节点数变化对定位误差影响实验中，锚节点始终保持着20%的比例。如图5所示，3种算法随着节点数增多变化较为平缓，定位精度稳步增长。GPLA算法略占优势，由于它在运动预测时运用了灰度预测模型，确定了大致的采样区域，相较其它两种算法的采样，这种方法产生的粒子有效性更大，总体能保持定位精度上的优势。在结果中还可以看到3种算法的定位误差差异基本保持稳定，说明节点数对算法性能差异影响不大。

图3 通信半径与平均定位误差关系

图4 锚节点数与平均定位误差关系

图5 节点数与平均定位误差关系

样本数直接影响定位算法的精度，从图6中可以看出，当样本为25时3种算法的定位误差趋向于稳定，样本继续增加也不会太多地提高定位精度。GPLA算法和EMCL算法随着样本增加定位误差越来越接近，是因为样本越大，其中包含的有效性粒子也会越多，两种算法的差异反而越小。样本的数量直接影响定位时间，选取合适的样本数对移动定位非常关键。

样本数对定位时间的影响非常大，实验对采用不同样本数时3种算法的定位时间做了对比。定位时间随着样本数的变化如图7所示，样本数较小时，3种算法定位时间相差不大，样本数超过30之后，就有明显区别了，GPLA算法用限制性的线性交叉，减少了重采样的时间消耗，比MCL算法要快很多，限制性线性交叉免去了重滤波的计算时间，因此比EMCL算法稍快。

实验还对未知节点在20个时间周期内的定位误差进行了对比，1个时间周期为1个步长，为了排除某些参数的影响，根据上述实验的结果，选取了接近稳定时的参数项，实验参数设置为：CN=250, CA=50,=50 m,=25,max=10 m。结果如图8所示。初始定位时，由于缺少先验值，3种算法定位误差都比较大，随着节点移动，GPLA算法在观测值增多和自我调节适应的情况下，很快达到较好的定位精度，由于它的强自适应性，可以保持较好的稳定性。另外两种算法则有不同程度的波动。此外，因为累积误差的影响，在后续定位中会使定位误差小幅度上升。

5 结束语

本文提供了一种针对移动节点定位的解决方案，其核心是基于蒙特卡罗定位算法的思想，通过灰度预测模型对节点运动状态进行预测、利用估计距离滤波、采用限制性线性交叉加快生成样本集，提高定位精度的同时，加强节点定位的自适应性，更接近于一种智能化的定位模式。最后通过在通信半径、锚节点数、节点数、样本数等条件变化的前提下，与其它算法进行了误差对比与分析，结果表明，GPLA算法在定位精度和定位时间上都有不同程度的提高，说明GPLA算法在某些条件下具有它的价值和优势，当然还有需要完善之处，比如如何减少累积误差的影响，如何使它更适合于稀疏网络等，都还需要更多的研究。

图6 样本数与平均定位误差关系

图7 样本数与定位时间关系

图8 步长与定位误差关系

[1] 任丰原, 黄海宁, 林闯. 无线传感器网络[J]. 软件学报, 2003, 14(7): 1282-1290.

Ren Feng-yuan, Huang Hai-ning, and Lin Chuang. Wireless sensor networks[J]., 2003, 14(7): 1282-1290.

[2] 钱志鸿, 王义君. 面向物联网的无线传感器网络综述[J]. 电子与信息学报, 2013, 35(1): 215-227.

Qian Zhi-hong and Wang Yi-jun. Internet of things-oriented wireless sensor networks review[J].&, 2013, 35(1): 215-227.

[3] 彭宇, 王丹. 无线传感器网络定位技术综述[J]. 电子测量与仪器学报, 2011, 25(5): 389-399.

Peng Yu and Wang Dan. A review: wireless sensor networks localization[J]., 2011, 25(5): 389-399.

[4] Kaltiokallio O and Bocca M. Real-time intrusion detection and tracking in indoor environment through distributed RSSI processing[C]. 2011 IEEE 17th International Conference at Toyama, 2011: 61-70.

[5] 毛永毅, 张颖. 非视距传播环境下的AOA定位跟踪算法[J]. 计算机应用, 2011, 31(2): 317-319.

Mao Yong-Yi and Zhang Ying. AOA location and tracking algorithm in non-line-of-sight propagation environment[J]., 2011, 31(2): 317-319.

[6] Zhang Weile, Yin Qinye, Xue Feng,.. Distributed TDOA estimation for wireless sensor networks based on frequency-hopping in multipath environment[C]. 2010 IEEE 71st, Taipei Vehicular Technology Conference (VTC 2010-Spring), 2010: 16-19.

[7] 程伟, 史浩山, 王庆文, 等. 基于差分修正的传感器网络加权质心定位算法[J]. 系统仿真学报, 2012, 24(2): 389-393.

Cheng Wei, Shi Hao-shan, Wang Qing-wen,.. Weighted centroid localization algorithm based on difference correction for sensor networks[J]., 2012, 24(2): 389-393.

[8] Cheng W, Li J, and Li H. An improved APIT location algorithm for wireless sensor networks[J].,2012, 139(1): 113-119.

[9] 肖丽萍, 刘晓红. 一种基于跳数修正的DV-Hop定位算法[J]. 传感技术学报, 2012, 25(12): 1726-1730.

Xiao Li-ping and Liu Xiao-hong. DV-Hop localization algorithm based on hop amendment[J]., 2012, 25(12): 1726-1730.

[10] Sun Xiao-ling, Chen Tao, Li Wei-qin.. Perfomance research of improved MDS-MAP algorithm in wireless sensor

networks localization[C]. Computer Science and Electronics Engineering (ICCSEE), Hangzhou, 2012: 587-590.

[11] Drawil N M, Amar H M, and Basi O A. GPS localization accuracy classification: a context-based approach[J].2013, 14(1): 262-273.

[12] Hu Ling-xuan and Evans D. Localization for mobile sensor networks[C]. Proceedings of MobiCom 2004, Philadelphia, Pennsylvania, USA, 2004: 45-57.

[13] 李敏, 罗挺, 徐华. 一种基于参考节点选择模型的无线传感器网络定位算法[J]. 传感技术学报, 2011 24(2): 264-268.

Li Min, Luo Ting, and Xu Hua. Localization algorithm based on anchor node select model for wireless sensor networks[J], 2011, 24(2): 264-268.

[14] 王洁, 王洪玉, 高庆华, 等. 一种适用于移动传感器网络的增强型蒙特卡罗定位跟踪算法[J]. 电子与信息学报, 2010, 32(4): 864-868.

Wang Jie, Wang Hong-yu, Gao Qing-hua,. Enhanced monte carlo localization and tracking algorithm for mobile wireless sensor network[J].&, 2010, 32(4): 864-868.

[15] 刘志华, 李改燕. 基于最小二乘法的蒙特卡罗移动节点定位算法[J]. 传感技术学报, 2012, 25(4): 541-544.

Liu Zhi-hua and Li Gai-yan. Monte-Carlo mobile node localization algorithms based on least squares method[J]., 2012, 25(4): 541-544.

[16] 朱海平, 于红丞, 钟小勇, 等. 动态无线传感器网络的改进蒙特卡罗定位算法[J]. 传感技术学报, 2012, 25(9): 1284-1288.

Zhu Hai-ping, Yu Hong-cheng, Zhong Xiao-yong,.. An improved monte carlo localization algorithm for mobile wireless sensor networks[J]., 2012, 25(9): 1284-1288.

[17] 刘思峰, 郭天榜, 党耀国, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 1999: 44-63.

Liu Si-feng, Guo Tian-bang, Dang Yao-guo,.. Grey System Theory and Its Application[M]. Beijing: Science Press, 1999: 44-63.

单志龙： 男，1976 年生，博士，教授，硕士生导师，研究方向为物联网、无线传感器网络、无线通信网络等.

刘兰辉： 女，1989年生，硕士生，研究方向为无线传感器网络.

张迎胜： 男，1988年生，硕士生，研究方向为无线传感器网络.

黄广雄： 男，1988年生，硕士生，研究方向为无线传感器网络.

A Strong Self-adaptivity Localization Algorithm Based on Gray Prediction Model for Mobile Nodes

Shan Zhi-long Liu Lan-hui Zhang Ying-sheng Huang Guang-xiong

(,,510631,)

Localization of sensor nodes is an important issue in Wireless Sensor Networks (WSNs), and positioning of the mobile nodes is one of the difficulties. To deal with this issue, a strong self-adaptive Localization Algorithm based on Gray Prediction model for mobile nodes (GPLA) is proposed. On the background of Monte Carlo Localization Algoritm, gray prediction model is used in GPLA, which can accurate sampling area is used to predict nodes motion situation. In filtering process, estimated distance is taken to improve the validity of the sample particles. Finally, restrictive linear crossover is used to generate new particles, which can accelerate the sampling process, reduce the times of sampling and heighten the efficiency of GPLA. Simulation results show that the algorithm has excellent performance and strong self-adaptivity in different communication radius, anchor node, sample size, and other conditions.

Wireless Sensor Networks (WSN); Localization; Mobile node; Gray prediction

TP393

A

1009-5896(2014)06-1492-06

10.3724/SP.J.1146.2013.01171

刘兰辉 lanhuilui1989@gmail.com

2013-08-02收到，2014-01-06改回

国家自然科学基金(61102065)，广州市科技计划项目(12C42091555)，广州市珠江科技新星专项(2011J2200083) 和广东省教育部产学研结合项目(2011B090400520)资助课题