基于连续相位频移键控调制的物理层网络编码检测及性能分析

沙 楠 高媛媛 益晓新 龙彦汕



基于连续相位频移键控调制的物理层网络编码检测及性能分析

沙 楠*高媛媛 益晓新 龙彦汕

(解放军理工大学通信工程学院 南京 210007)

针对双向中继信道，该文提出一种基于连续相位频移键控(CPFSK)调制的物理层网络编码(PNC)机制，即CPFSK-PNC。与已有的采用BPSK, QPSK等调制方式的物理层网络编码相比，该机制引入CPFSK的技术优势，提高了系统的频谱效率和功率效率。该文对瑞利衰落信道中CPFSK-PNC的物理层网络编码检测进行了研究。首先，利用CPFSK信号的记忆特性，根据最大似然准则设计了中继节点的物理层网络编码检测方案；其次，分析了信号之间最小欧氏距离并给出中继检测的平均误比特率下边界；最后，仿真验证了理论分析结果。

物理层网络编码；连续相位频移键控；最大似然；最小欧式距离

1 引言

2 系统模型

本文考虑双向单中继信道，如图1所示，研究采用检测转发协议的2时隙物理层网络编码方案。假设两个信源节点和之间没有直传链路，需借助中继节点分别传输各自的信息给对方，所有节点均配置单天线并工作在半双工模式，中继节点可以获得完美的上行信道状态信息。为了简化，所有节点采用2CPFSK调制，分析结果可以简单扩展到多进制CPFSK调制。

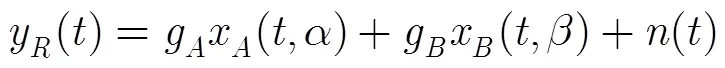
其中是信源到中继R的信道系数， , ，本文考虑准静态衰落信道，即在一帧数据内(假设一帧含个符号，)信道参数是恒定的，但是每一帧之间是独立变化的；为中继R处的零均值复高斯随机变量，单边功率谱密度为。定义符号序列满足，即中的元素，其中表示两个信源的比特信息异或对应的符号逻辑关系，这里定义为。中继节点R 对接收的混合信号进行PNC检测，得到的估计值。在第2时隙，R对检测序列进行CPFSK调制得到并广播给A和B。信源节点对接收信号进行CPFSK解调，再利用自身信息通过异或操作即可得到对方信息。其中A和B信息交换的关键是在多址接入阶段中继节点实现PNC检测得到，该过程很大程度上影响系统的误码率，此外由于目前已有大量文献研究了单路CPFSK信号的接收问题，因此本文不再研究源端的检测，而是重点研究中继节点的PNC检测。

3 中继PNC检测方案及性能分析

3.1 最大似然序列检测算法

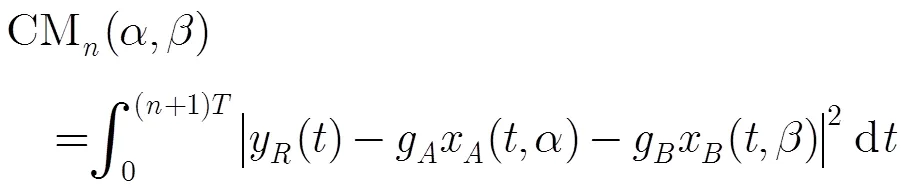
式(6)可重新表示为

3.2 性能分析

评估采用最大似然序列检测的信号误码性能最简单有效的参数是所有可能信号对之间的最小欧式距离，差错性能可表示为[18]

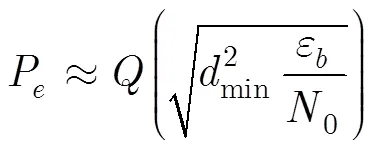
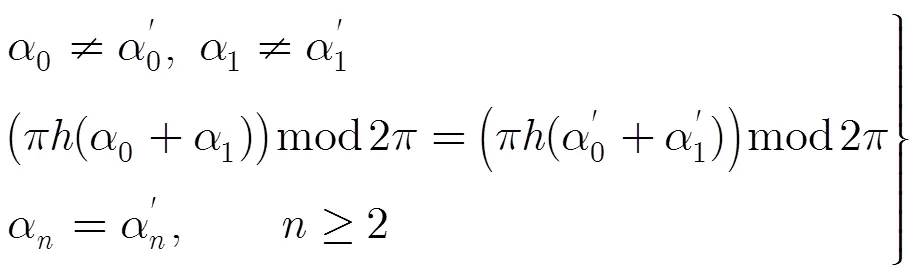
由此得到单路2CPFSK信号归一化最小平方欧式距离的上边界[15]。

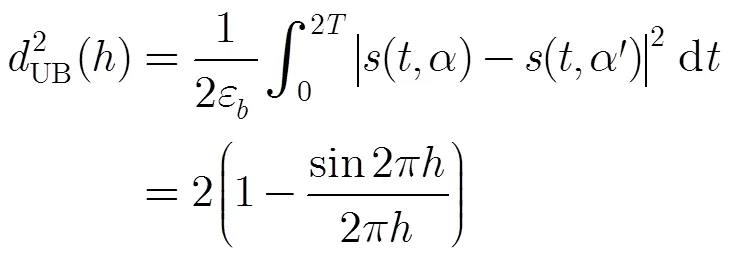
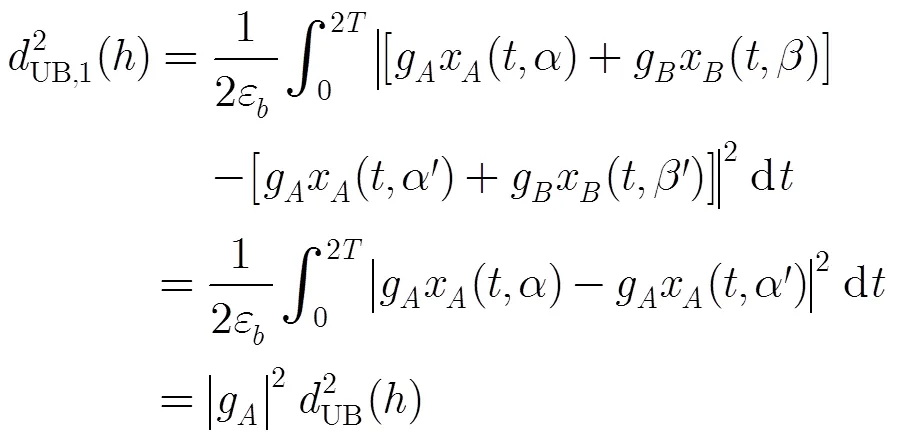
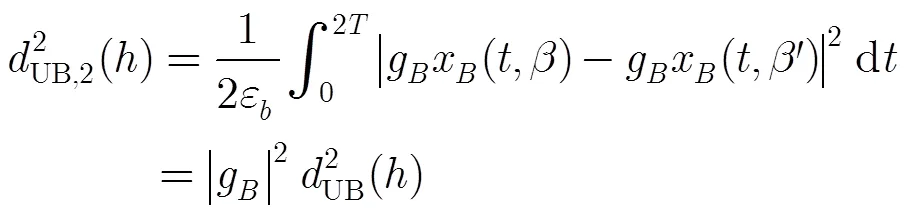
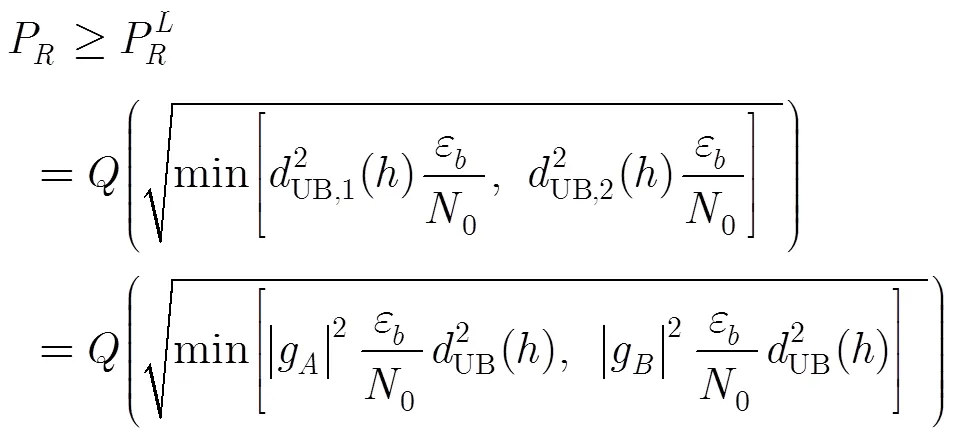
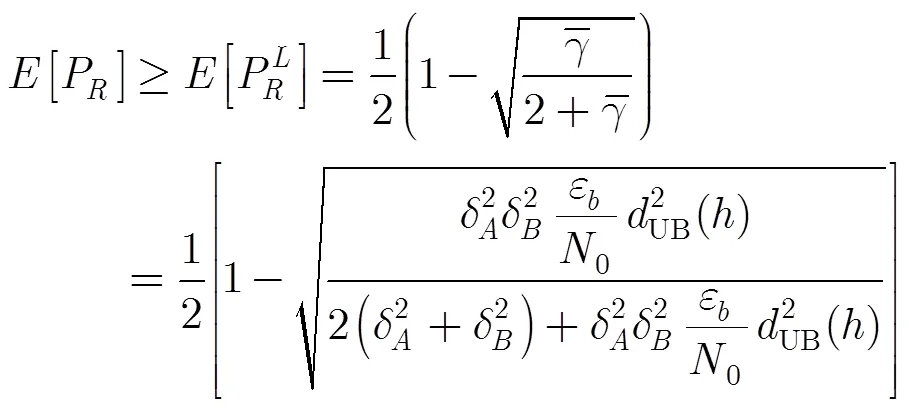
4 仿真结果

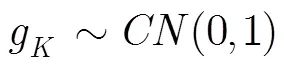
BPSK, QPSK等线性调制方式使用传统的非线性功率放大器效率不佳，且存在非线性失真现象，而CPFSK信号本身具有恒包络特性，能够适用高效率的C类高功率放大器，从而提高系统的功率效率。通过本节仿真还可以看出，在系统的误码性能或频谱效率方面，CPFSK调制方式也比BPSK, QPSK等线性调制方式具有更大的优势。值得注意的是，对于CPFSK-PNC系统，调制指数是重要参数，调制指数越小，频谱特性越好，但误码性能越差。因此在系统设计中，要根据实际场景和需求选择合适的调制指数。例如，当信道条件较差时，为提高误码性能，可以选择较大的调制指数；当信道带宽受限时，为提高频谱效率，可以选择较小的调制指数。

图3 中继PNC检测的平均误比特率性能

图4 端到端的平均误比特率性能

图5 信号功率密度谱

5 结束语

本文将CPFSK调制技术应用于双向中继信道的物理层网络编码中，提出了CPFSK-PNC机制。利用中继叠加信号的记忆特性，根据最大似然准则设计了中继节点的物理层网络编码检测方案，通过信号之间最小欧氏距离推导了中继检测的平均误比特率下边界，在此基础上仿真验证了所提方案的误码性能。分析和仿真结果表明，选择合适的调制指数可以使得CPFSK-PNC系统获得优于现有调制方式下(如BPSK, QPSK)PNC系统的误码性能。此外，CPFSK本身的技术优势还使得CPFSK-PNC系统具有较好的功率效率和频谱效率。同步问题是物理层网络编码实现的难点问题，同步误差对系统的性能有很大影响，CPFSK技术的一个显著优势是可以采用非相干解调，因此，有关CPFSK-PNC系统的中继非相干检测算法值得进一步研究。此外，信道编码、调制和物理层网络编码三者的联合设计是目前PNC研究的热点之一，CPFSK信号本身具有的网格编码特性，可以进一步提高编码增益，因此，如何充分开发CPFSK的编码特性，将信道编码与CPFSK-PNC系统相结合也是值得深入研究的问题。

[1] Katti S, Gollakota S, and Katabi D. Embracing wireless interference: analog network coding[C]. Proceedings of ACM SIGCOMM2007, Kyoto, Japan, 2007: 397-408.

[2] Zhang S, Liew S C, and Lam P P. Hot topic: physical layer network coding[C]. Proceedings of MobiCom 2006, Los Angeles, CA, USA, 2006: 358-365.

[3] 颜伟, 蔡跃明, 潘成康. 双向中继信道中物理层网络编码的检测[J]. 通信学报, 2012, 33(2): 82-86.

[4] MinChul J and Il-Min K. Error performance analysis of BPSK modulation in physical-layer network-coded bidirectional relay networks[J]., 2010, 58(10): 2770-2775.

[5] Noori M and Ardakani M. On symbol mapping for binary physical-layer network coding with PSK modulaton[J]., 2012, 11(1): 21-26.

[6] Duc T and Jinho C. Convolutional codes in two-way relay networks with physical-layer network coding[J]., 2010, 9(9): 2724-2729.

[7] 陈志成, 郑宝玉, 吉晓东. 一种信道编码与物理层网络编码的联合设计[J]. 信号处理, 2011, 27(5): 658-663.

[8] 陈志成, 郑宝玉, 吉晓东, 等. 一种基于TCM的信道编码与物理层网络编码的联合设计[J]. 电子与信息学报, 2011, 33(11): 2594-2599.

[9] Hassan A, Bin D, Huang B,.. Joint design of channel coding and network coding of different channel models for wireless networks[C]. IEEE 3rd ICCSN, Xi’an, China, 2011: 46-51.

[10] 池新生, 郑宝玉, 陈志成, 等. 非对称速率的双向中继信道物理层网络编码[J]. 信号处理, 2012, 28(4): 500-506.

[11] 魏浩, 郑宝玉, 侯晓赟, 等. 不对称速率双向中继传输策略研究[J]. 电子与信息学报, 2012, 34(11): 2748-2754.

[12] Lu L and Liew S C. Asynchronous physical-layer network coding[J]., 2012, 11(2): 819-831.

[13] 吴厚明, 江桦, 崔伟亮. 基于循环平稳性的CPM信号调制阶数盲识别算法[J]. 信号处理, 2012, 28(3): 432-436.

[14] Rimoldi B E. A decomposition approach to CPM[J]., 1988, 34(2): 260-270.

[16] Lindell G, Sundberg C E, and Aulin T. Minimum Euclidean distance for combinations of short rate l/2 convolutional codes and CPFSK modulation[J]., 1984, 30(3): 509-519.

[17] Tung C C and Livingston J N. Viterbi detector for narrow-band digital FM with limiter-discriminator detection[C]. Proceedings of GLOBECOM, San Francisco, USA, 1994: 201-205.

[18] Fonseka J. Soft-decision phase detection with Viterbi decoding for CPM signals[J]., 1999, 47(12): 1802-1810.

[19] Proakis J G. Digital Communications[M]. 5th Ed., New York: McGraw-Hill College, 2009, Chap. 3-4.

[20] Xiong F. Digital Modulation Techniques[M]. 2nd Ed., London: Artech House, 2006, Chap. 6.

[21] Song L Y, Hong G, Jiao B L,. Joint relay selection and analog network coding using differential modulation in two-way relay channels[J].2010, 59(6): 2932-2939.

[22] Simon M K and Alouini M S. Digital Communication over Fading Channels[M]. 2nd Ed., New York: Wiley, 2004, Chap. 5-8.

沙 楠： 男，1981年生，讲师，博士生，研究方向为网络编码、协同通信.

高媛媛： 女，1968年生，教授，硕士生导师，研究方向为编码与调制、无线通信与信号处理.

益晓新： 男，1951年生，教授，博士生导师，研究方向为宽带通信网络、通信信号处理.

龙彦汕： 女，1989年生，硕士生，研究方向为协同通信、跳频通信.

Physical-layer Network Coding Based on CPFSK ModulationDetection and Performance Analysis

Sha Nan Gao Yuan-yuan Yi Xiao-xin Long Yan-shan

(,,210007,)

A Physical-layer Network Coding (PNC) scheme based on Continuous Phase Frequency Shift Keying (CPFSK) modulation, i.e., CPFSK-PNC, for two-way relay channels is proposed. Compared with the current schemes of BPSK or QPSK for PNC, the CPFSK-PNC scheme, by exploitating the technical advantage of the CPFSK method, hashigher power and spectral efficiency.The detection for the relay receiver in the CPFSK-PNC scheme over Rayleigh fading channels is investigated.Firstly, in the light of the memory property of the CPFSK signal, the detection method for PNC at the relay based on the Maximum-Likelihood (ML) criterion is designed. Secondly, the minimum Euclidean distance is analyzed and the tight lower bound for the average bit error rate at the relay is derived. And finally, the simulation results verify the theoretical asymptotic derivations.

Physical-layer Network Coding (PNC); Continuous Phase Frequency Shift Keying (CPFSK); Maximum-Likelihood (ML); Minimum Euclidean distance

TN925

A

1009-5896(2014)06-1454-06

10.3724/SP.J.1146.2013.01201

沙楠 njshanan@163.com

2013-08-06收到，2013-12-02改回

国家自然科学基金(60972050)和国家重大专项(2010ZX03003-003- 01)资助课题