同时同频全双工场景中的射频域自适应干扰抵消

王 俊 赵宏志 卿朝进② 唐友喜



同时同频全双工场景中的射频域自适应干扰抵消

王 俊①赵宏志①卿朝进①②唐友喜*①

①(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)②(西华大学电气信息学院 成都 610039)

考虑同时同频全双工无线收发信机的射频域自干扰抵消技术，现有研究多集中于利用手动方式调整自干扰估计信号的参数。针对这一问题，该文提出一种射频域的自适应干扰抵消算法。以正交、同相参考支路构成的自干扰估计结构为基础，利用梯度下降法搜索支路的最优权矢量，估计出自干扰信号，实现了射频域的自适应干扰抵消，并且给出了该算法的收敛性分析。分析与仿真表明，当迭代步长越大或统计时间越短时，算法的收敛速度越小。在100倍符号周期的统计时间，0.3的归一化步长，80 dB干信比以及0 dB信噪比的仿真条件下，该文提出的射频域自适应干扰抵消算法可以实现约100 dB的自干扰抑制。

无线通信；同时同频全双工；射频域干扰抵消；收敛性

1 引言

在同时同频全双工传输模式的收发信机中，接收信号受到了来自本地发送信号的大功率干扰。由于模数转换器(Analog to Digital Converter, ADC)的动态范围有限，在进入ADC之前接收信号干信比必须降低到一定水平[6]。因此，在同时同频全双工系统中，射频域的自干扰抵消技术研究尤为重要。

在已有的同时同频全双工射频域自干扰抵消技术中，文献[7, 8]利用本地发送射频信号作为自干扰信号的参考，通过改变参考信号的相位和幅度，分别在2.4 GHz频段、530 MHz频段验证了射频域自干扰抵消的可行性；文献[9, 10]则采用由正交、同相两条支路构成的自干扰信号估计结构，通过手动方式调整两支路的衰减器增益，实现了在2.4 GHz频段的射频域自干扰抵消方案验证。虽然文献[7~10]验证了射频域自干扰抵消方案的可行性，但是它们均未给出参考信号参数调整的具体方法，无法直接应用于实际的通信系统。

针对这个问题，本文以正交、同相参考支路构成的自干扰估计结构为基础，首先对接收信号强度与两支路权矢量之间的关系进行了理论分析；进而提出了一种射频域的自适应干扰抵消算法；然后分析了该算法的收敛性，并讨论了干信比、统计时间、迭代步长等参数对收敛速度的影响；最后进行了仿真验证。

本文结构如下：第2节给出同时同频全双工系统模型；第3节详细阐述射频域自适应干扰抵消算法；第4节分析该算法的收敛性；仿真结果在第5节中给出；第6节为本文的结论。

2 系统模型

本文采用的同时同频全双工系统模型如图1所示[9]，系统包括近端与远端两个收发信机。为了便于分析，本文以近端收发信机为例，阐述其射频域自干扰抵消算法。为便于标识，用下标表示近端发射信号参数，下标表示远端发射信号参数。

2.1发射机模型

其中

2.2 信道模型

2.3 接收机模型

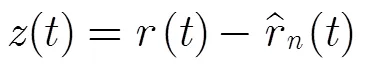
干扰抵消后的信号经过下变频、模数转换、匹配滤波后，解调得到远端发送比特流的估计值。

3 干扰抵消算法

3.1 干扰抵消结构

根据三角函数的和差化积恒等式，式(5)中的近端自干扰信号项可写为

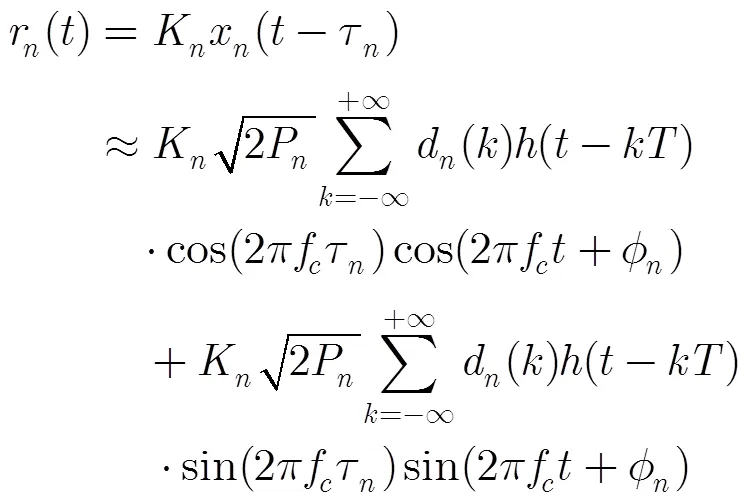
因此，射频域近端自干扰信号的估计可以转化为参数, 的估计。不妨定义, 分别为参数, 的估计值。根据式(14)，本文采用的射频域自适应干扰抵消结构如图2所示。

3.2 基于梯度下降法的自适应干扰抵消

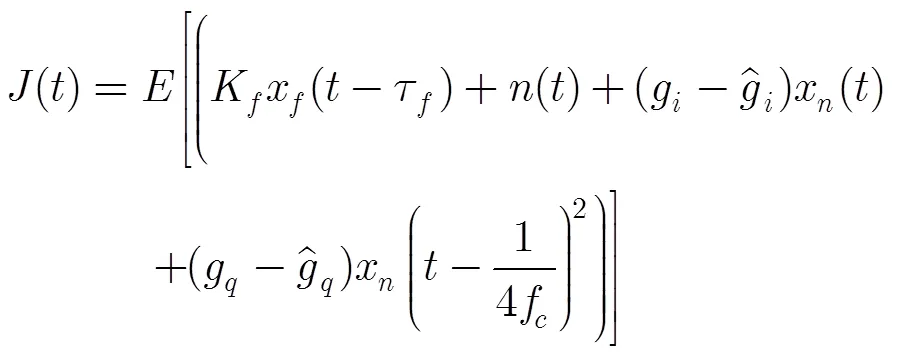
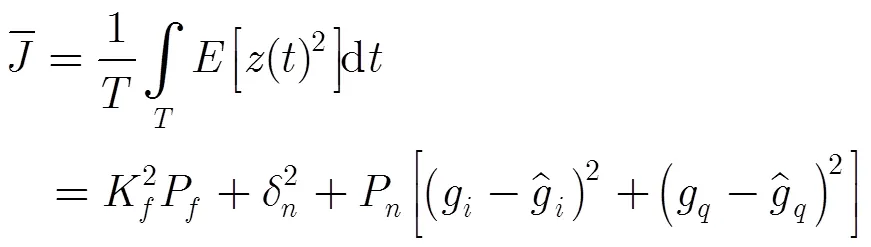
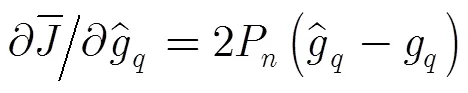
其中

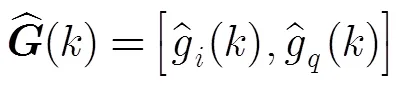
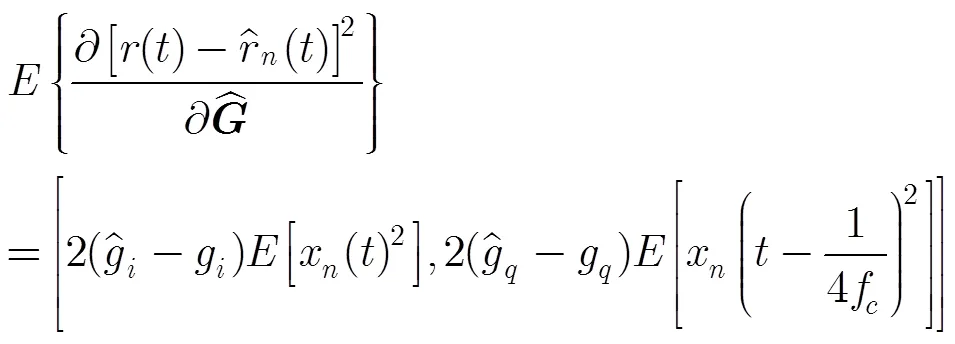
综上所述，在同时同频全双工场景中，在图2所示的自适应干扰抵消结构中，射频域自适应干扰抵消步骤如下：

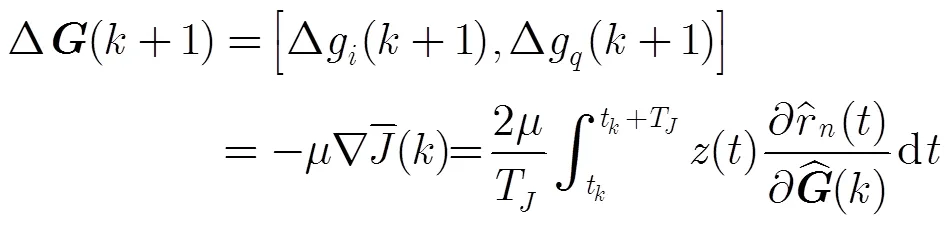
其中

并控制修改同相、正交两支路的增益；

步骤4 重复步骤2。

4 性能分析

4.1收敛性分析

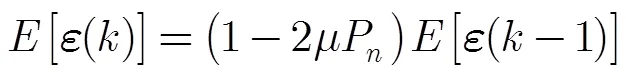
则第步迭代的误差矢量与初始误差矢量的关系为

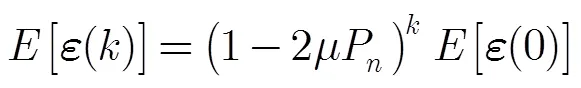
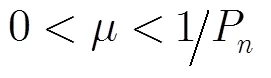
综上所述，当式(32)的条件满足时，本文的射频域自干扰抵消算法是收敛的。

4.2 收敛速度分析

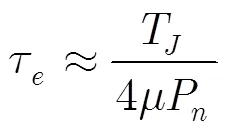
5 数值与仿真结果

表1 数值与仿真分析的参数设置

需要指出的是，由于文献[7~10]只是对射频干扰抑制进行可行性验证，并且仅给出了在特定实验环境中干扰抑制的实际测量结果，该方案很难重建以及评估性能。因此，本文没有与上述文献中的方案进行仿真对比。

综上所述，考虑同时同频全双工传输场景，针对加性白高斯噪声无线传播信道，在加性白高斯噪声无线自干扰信道中，本文提出的射频域自适应干扰抵消算法能够实现对干扰信号的自适应抵消。结合式(35)可知，当迭代步长越大或统计时间越短时，算法的收敛速度越快。从仿真结果中容易看出：在2.4 GHz载频、5 MHz带宽、BPSK调制、0 dB信噪比，100倍符号周期的统计时间，0.3的归一化步长以及80 dB干信比的仿真条件下，同时同频全双工场景中的射频域自适应干扰抵消算法，可以实现约100 dB的自干扰抵消效果。

6 结束语

本文考虑同时同频全双工传输场景，针对加性白高斯噪声无线传播信道，在加性白高斯噪声无线自干扰信道中，提出了一种射频域的自适应干扰抵消算法；并分析了该方法的收敛性以及收敛速度。分析和仿真表明，本文提出的射频域自适应干扰抵消算法能够实现同时同频全双工场景中的自干扰抵消，并且当迭代步长越大或单次统计时间越短时，算法的收敛速度越快。本文的研究成果为同时同频全双工技术的实现提供了理论支持。

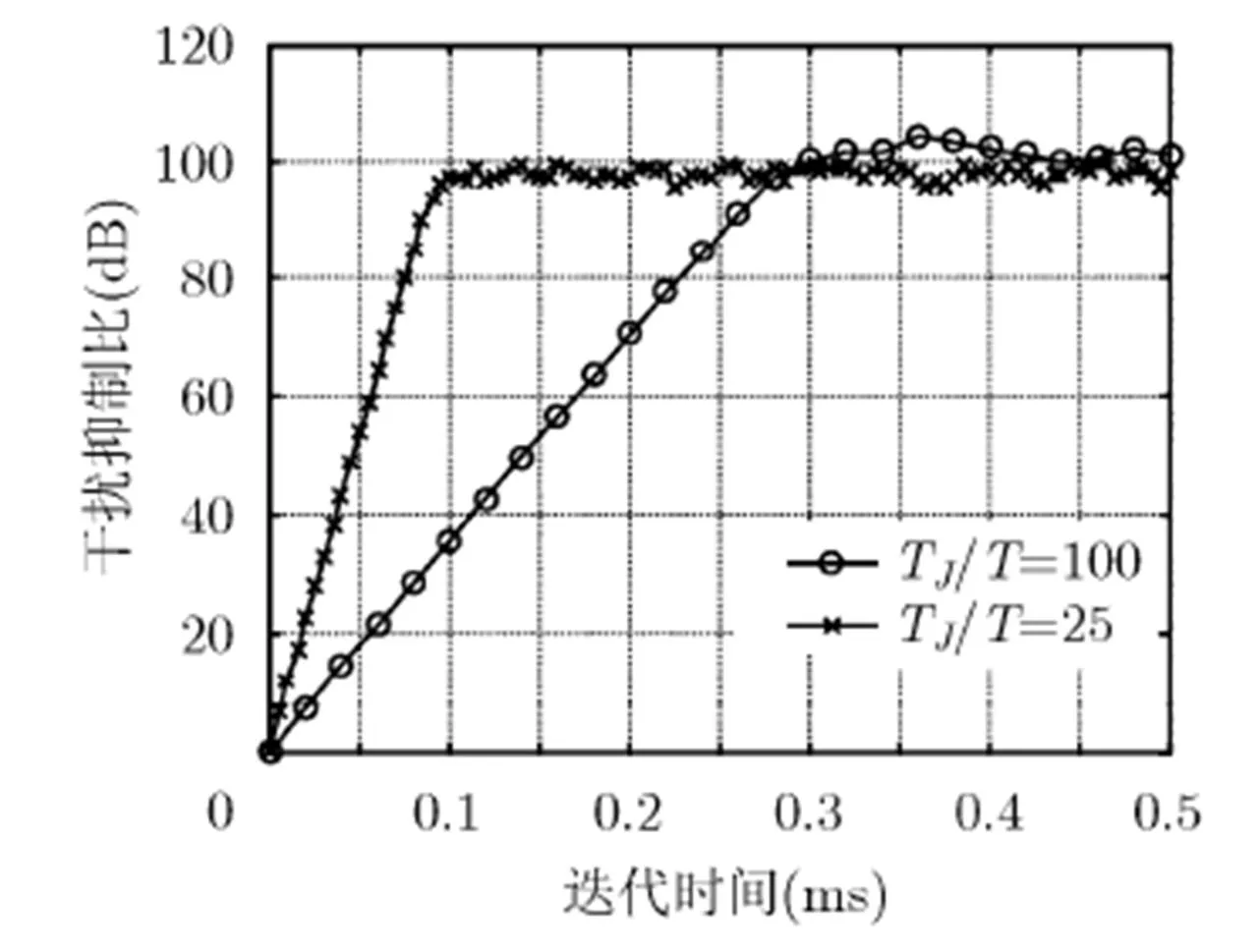
图3 不同单次迭代统计时间下，干扰抑制比随迭代时间的变化

图4 不同归一化迭代步长下，干扰抑制比随迭代时间的变化

图5 不同干信比下，干扰抑制比随迭代时间的变化

[1] Rappaport T S, Shu S, Mayzus R,.. Millimeter wave mobile communications for 5G cellular: it will work![J]., 2013, 1: 335-349.

[2] Cadambe V R and Jafar S A. Degrees of freedom of wireless networks with relays, feedback, cooperation, and full duplex operation[J]., 2009, 55(5): 2334-2344.

[3] Elsayed A, Eltawil A M, and Sabharwal A. Rate gain region and design tradeoffs for full-Duplex wireless communications [J]., 2013, 12(7): 3556-3565.

[4] López-Valcarce R, Antonio-Rodríguez E, Mosquera C,An adaptive feedback canceller for full-duplex relays based on spectrum shaping[J]., 2012, 30(8): 1566-1577.

[5] 张志亮, 罗龙, 邵士海, 等. ADC量化对同频全双工数字自干扰消除的误码率性能分析[J]. 电子与信息学报, 2013, 35(6): 1331-1337.

Zhang Zhi-liang, Luo Long, Shao Shi-hai,Analysis of ADC guantizing affection on SER performance of self-interference canceling common-frequency full-duplex system[J].&, 2013, 35(6): 1331-1337.

[6] Oppenheim A and Schafer R. Discrete Time Signal Processing[M]. 3rd Ed., New Jersey: Prentice Hall Inc, 2009: 183-197.

[7] Choi J I, Jain M, Srinivasan K,.. Achieving single channel, full duplex wireless communication[C]. MobiCom’10, New York, USA, 2010: 1-12.

[8] Radunovic B, Gunawardena D, Key P,.. Rethinking indoor wireless mesh design: low power, low frequency, full-duplex[C]. WIMESH, Boston, Massachusetts, 2010: 1-6.

[9] Jain M, Choi J, Kim T M,Practical, real-time, full duplex wireless[C]. Mobile Computing and Networking, New York, USA, 2011: 301-312.

[10] Hong S, Mehlman J, and Katti S. Picasso: flexible RF and spectrum slicing[C]. SIGCOMM’12, Helsinki, Finland, 2012: 13-17.

[11] Gordon L S. Principles of Mobile Communication[M]. 3rd Ed.,Berlin: Springer, 2011: 198-203.

[12] Andreas F M.Wireless Communications[M]. 2nd Ed., New York: Wiley, 2010: 101-103.

[13] Napolitano A. Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications[M]. New York: Wiley, 2012: 45-121.

[14] Boyds S, Stephen P,.. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004: 463-483.

[15] Widrow B, McCool J M, Larimore M,.. Stationary and nonstationary learning characteristics of the LMS adaptive filter[J]., 1976, 64(8): 1151-1162.

[16] Rumberg B and Graham D W. A low-power magnitude detector for analysis of transient-rich signals[J]., 2012, 47(3): 676-685.

王 俊： 女，1988年生，博士生，研究方向为无线通信信号处理、通信抗干扰技术等.

赵宏志： 男，1978年生，副教授，研究方向为无线通信信号处理、通信抗干扰技术、并行化通信信号处理等.

卿朝进： 男，1978年生，副教授，研究方向为无线与移动通信中的信号处理、分布式天线系统、时频同步、压缩感知等.

唐友喜： 男，1964年生，教授，博士生导师，研究方向为无线通信中的信号处理、传感器网络等.

Adaptive Self-interference Cancellation at RF Domain in Co-frequency Co-time Full Duplex Systems

Wang Jun①Zhao Hong-zhi①Qing Chao-jin①②Tang You-xi①

①(,,611731,)②(,,610039,)

In the context of the RF domain self-interference cancellation algorithms in the co-frequency and co-time full duplex system, the current research focuses mainly on the manually adjusting of self-interference parameters. To solve this problem, a RF domain adaptive self-interference cancellation is proposed. On the basis of the self-interference estimation construction within an in-phase and quadrature reference signal channels, the self-interference is reconstructed by searching the optimal weight vector with the method of gradient descending and cancelled at last. In addition, the convergence of the proposed algorithm is analyzed. The analysis and simulation show that the convergent speed is faster when the iterative step size is larger and the statistical time is shorter. The self-interference can decrease almost 100 dB adopting the RF domain adaptive self-interference cancellation algorithm proposed in this paper, when the statistical time is 100 symbol periods, the normalized iterative step is 0.3, the signal to noise ratio is 0 dB, and the interference to signal ratio is 80 dB.

Wireless communication; Co-frequency and Co-time Full Duplex (CCFD); RF self-interference cancellation; Convergence

TN92

A

1009-5896(2014)06-1435-06

10.3724/SP.J.1146.2013.01187

唐友喜 tangyx@uestc. Edu. cn

2013-08-06收到，2013-12-16改回

国家自然科学基金(U1035002/L05, 61001087, 61101034, 61271164)，国家科技重大专项(2011ZX03003010-003, 2014ZX03003001-002)和四川省教育厅重点项目(12ZA161)资助课题