基于非均匀FFT的长时间相参积累算法

田 超 文树梁



基于非均匀FFT的长时间相参积累算法

田 超*文树梁

(中国航天二院23所 北京 100854)

针对采样引起时域相参积累损失以及相参积累算法运算量较大的问题，该文提出一种在快时间频域实现长时间相参积累的快速算法。该算法在快时间频域利用非均匀快速傅里叶变换(FFT)校正距离走动，完成相位补偿，然后通过快速逆傅里叶变换(IFFT)实现积累。该算法可以避免由采样引起的积累损失且运算量相对较小，理论分析和仿真结果验证了该算法的有效性。

雷达信号处理；长时间相参积累；非均匀FFT；运动补偿

1 引言

文献[5-8]利用Hough变换将匀速运动目标检测转化为直线检测问题，可以实现长时间的非相参积累，该方法运算量相对较小，但在低信噪比时性能下降明显。文献[9]将回波数据分帧处理，帧内相参积累，帧间利用Hough变换进行非相参积累，相比于文献[5]，其低信噪比下目标检测性能提高的程度取决于帧内相参积累效果。文献[10]则将速度的搜索范围分成若干段，段内进行相同的距离走动校正后利用MTD进行相参积累，段间进行峰值判定以实现目标检测，在速度搜索范围一定时，分段越细，目标检测性能越高，运算量亦越大。文献[11]通过Keystone变换校正距离走动，然后利用MTD进行相参积累，对于匀速运动目标，该方法积累效果好，但实现该变换需要进行sinc插值，运算量较大。文献[12]提出的Radon-Fourier变换方法先通过初始距离和径向速度的2维搜索确定目标运动轨迹，然后通过一组多普勒滤波器组实现长时间相参积累，该方法积累效果好，但运算量大。文献[13,14]则针对Radon-Fourier变换运算量大的问题，在不损失检测性能的前提下提出了基于Chirp Z变换的快速实现算法，大大减小了运算量。综合地看，非相参积累，相参和非相参混合积累，相参积累方法的积累性能依次提高，运算量依次增大。

本文综合考虑积累性能和运算量，主要研究如何在不降低积累性能的条件下，以较小的运算量实现长时间相参积累。先详细分析了采样引起时域积累损失的原因，并给出了采样率与积累损失的近似关系，然后提出一种在快时间频域实现相参积累的快速算法。该算法在快时间频域先利用非均匀快速傅里叶变换进行目标回波的运动补偿，然后通过IFFT完成相参积累。在保证积累性能的同时，该算法的运算量小于常用相参积累算法。

2 运动目标的回波模型

假设雷达发射的信号为线性调频脉冲

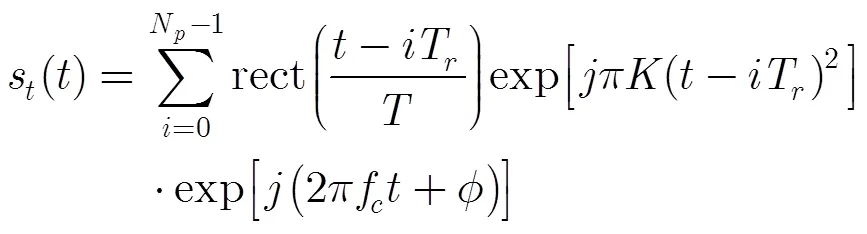
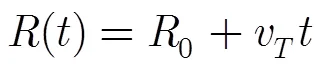
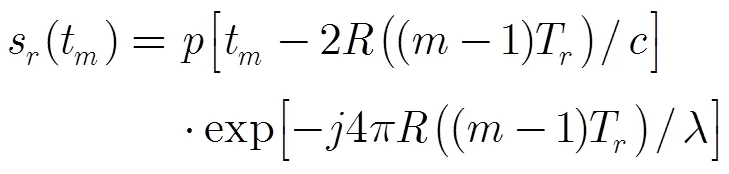
相应的快时间维频谱为[15]

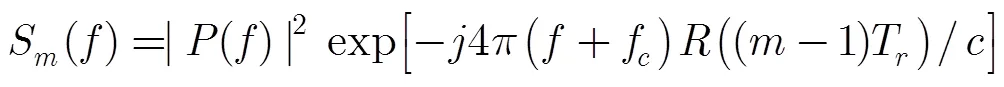
3 时域相参积累损失分析

图1 不同脉冲回波初始采样点相对位置示意图

而相应匹配滤波器的冲激响应为

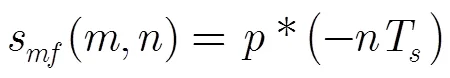
此时匹配滤波的输出为

按照在时域通过初始距离和速度2维搜索来对齐包络并补偿相位的思路，当搜索值与真实值完全匹配时，积累的结果为

通过推导，近似可得积累峰值为

4 快时间频域基于非均匀FFT的积累方法

在快时间频域经匹配滤波的输出可依据式(6)求得，为

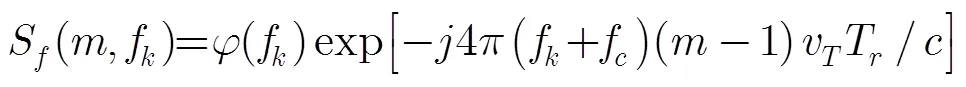
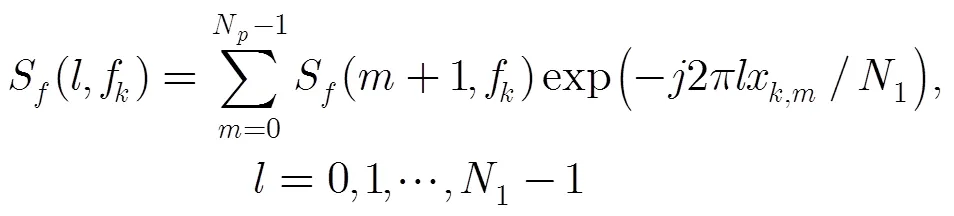
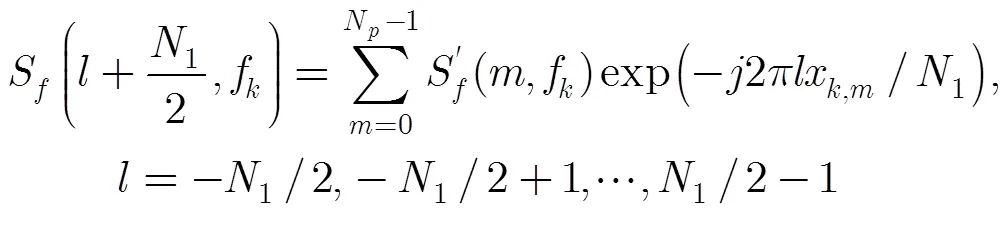
而由文献[16]可知

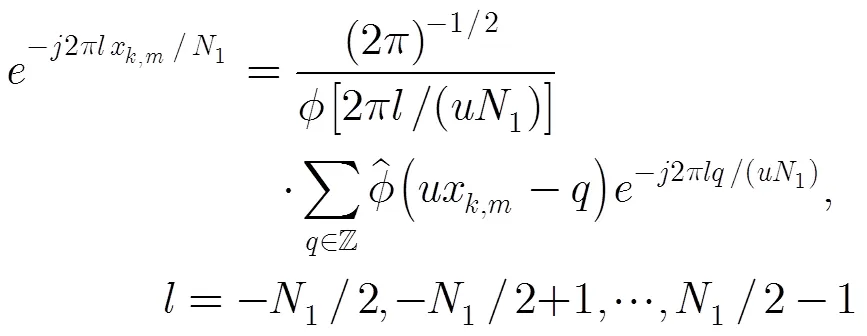
其中

将式(19)代入式(18)并经过推导，可得

至此，式(15)非均匀傅里叶变换的计算转化为常规的DFT，从而可通过FFT达到快速计算的目的。整个非均匀快速傅里叶变换的实现过程可分为3步：

结合上述分析并将匹配滤波所需的计算量统计在内，可得到实现基于Radon-Fourier 变换(RFT)，Keystone变换(KT),Chirp Z变换(CZT)和非均匀FFT(NUFFT)的长时间相参积累方法需要的总计算量，如表1所示。

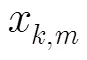
5 仿真结果及分析

本节将通过数值仿真验证第3节中有关积累损失的结论，并给出本文方法与其它常用积累算法性能和计算量的对比。

表1 4种相参积累算法计算复杂度对比

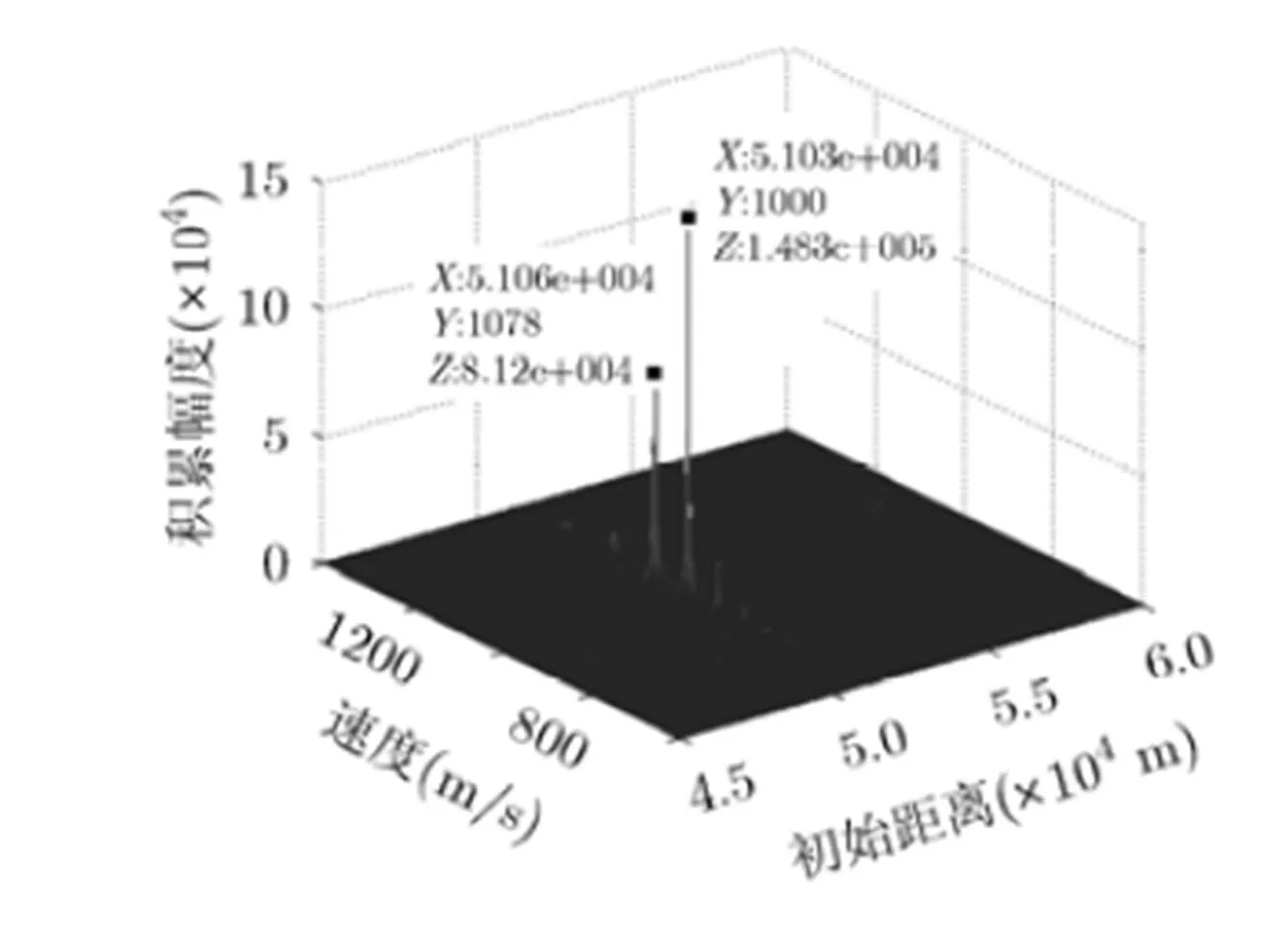
图2 包络对齐相位补偿后积累效果()

图3 包络对齐后包络积累效果()

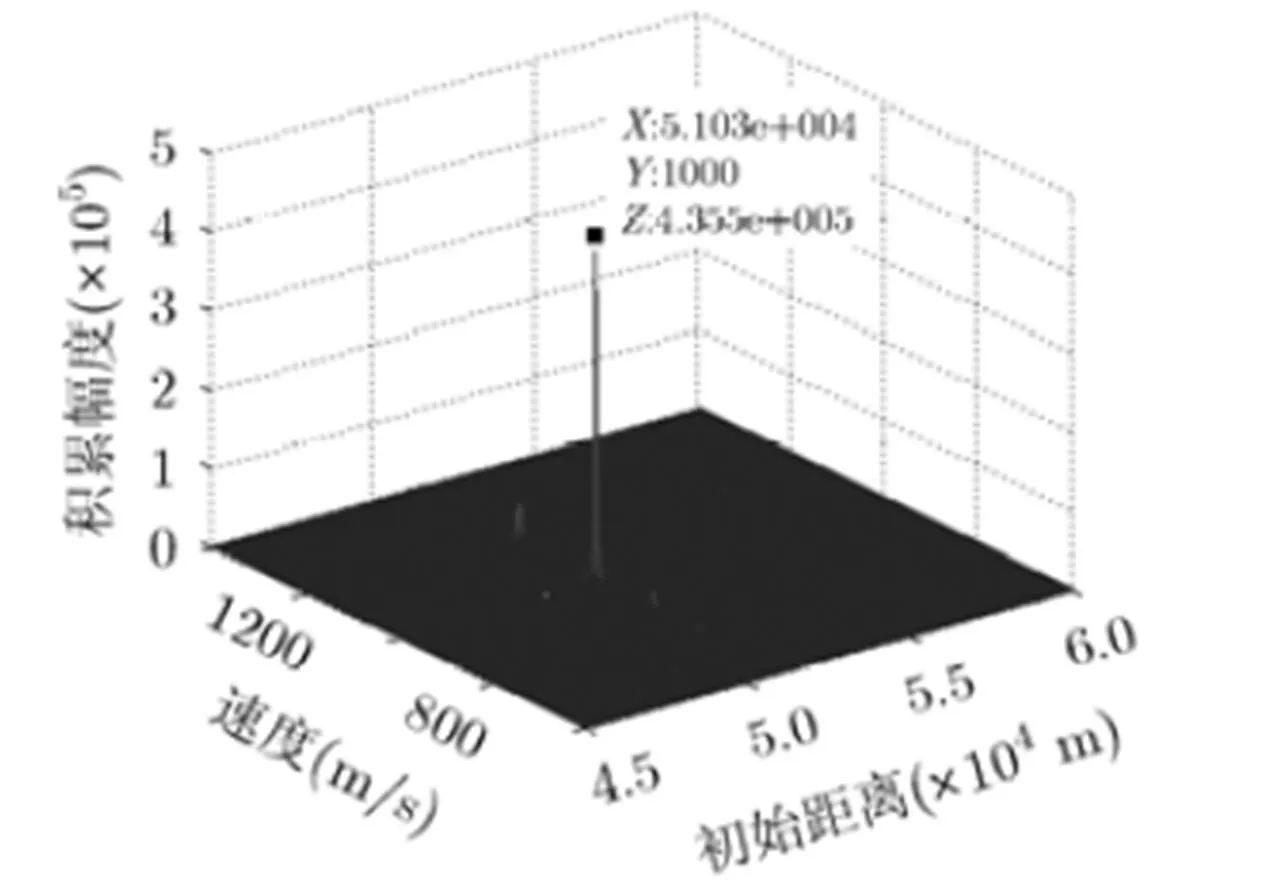
图4 包络对齐相位补偿后积累效果()

图5 包络对齐后包络积累效果()

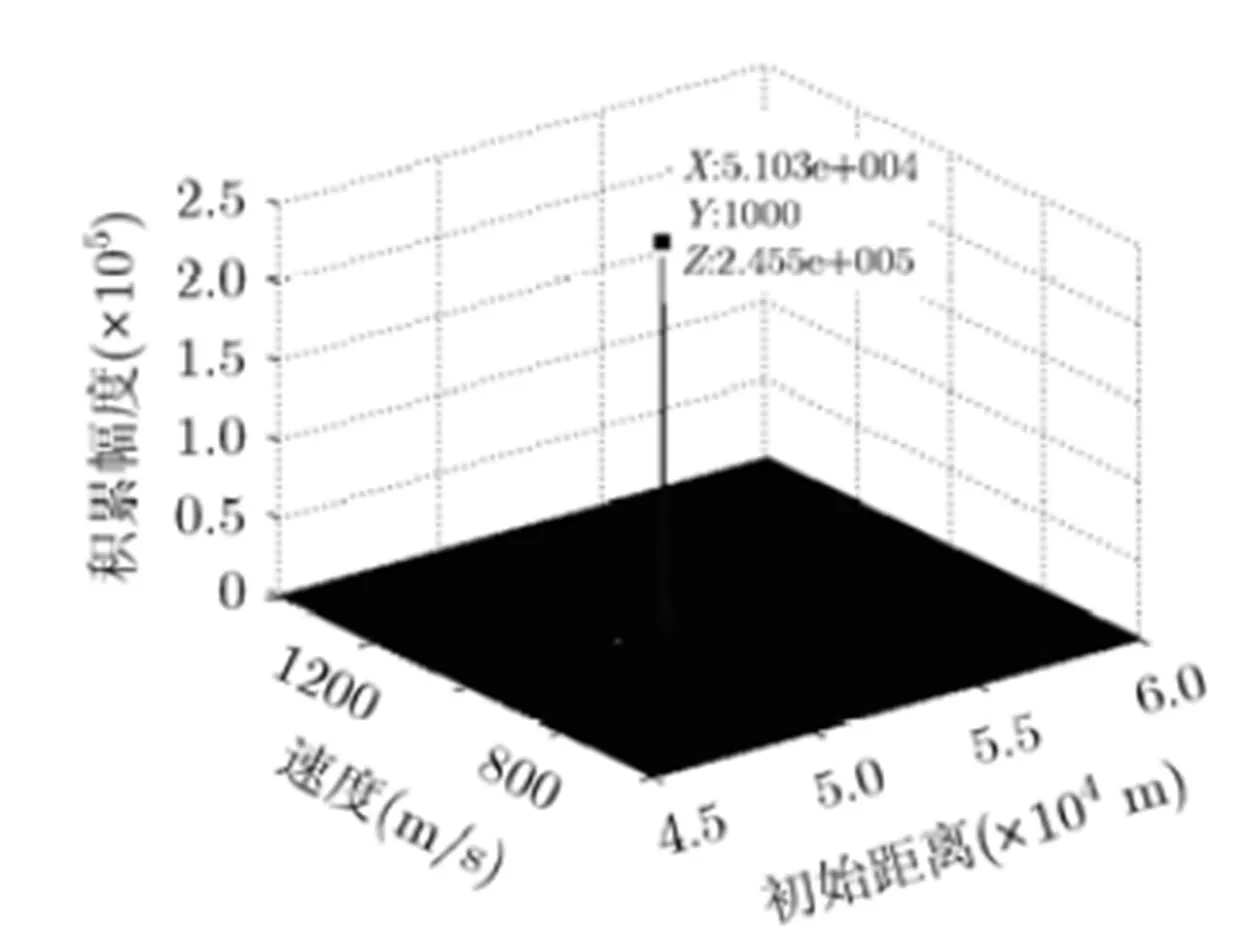
图6 利用NUFFT作运动补偿后积累效果()

图7 利用非均匀FFT作运动补偿后积累效果()

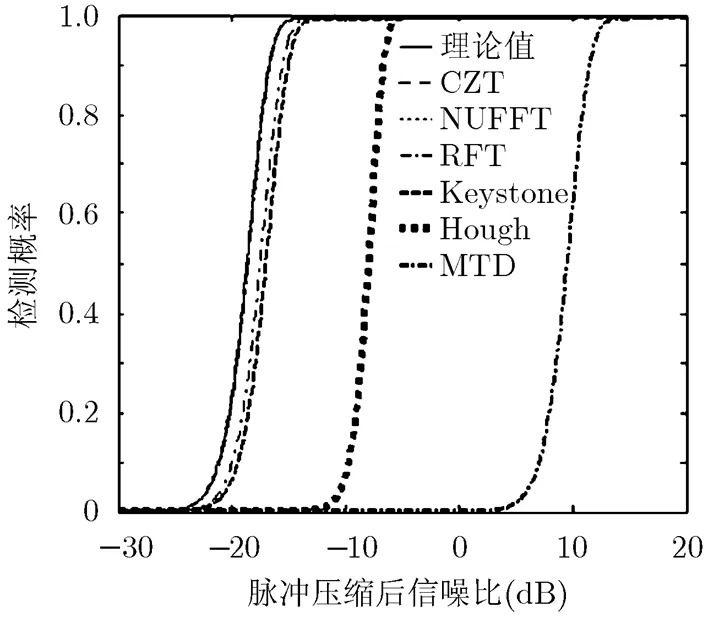
图8 不同积累算法积累后检测性能对比

随着积累脉冲数的增加，由图9(a)可知，4种算法计算量随之增大，由图9(b)可知基于Radon- Fourier变换，Keystone变换的积累算法计算量增加的速度快于基于Chirp Z变换的算法和本文算法。积累脉冲数为1000时，基于Radon-Fourier变换，Keystone变换，Chirp Z变换的积累算法所需复数乘法次数依次为2.5×1010, 1.3×1010, 1×109，约为本文算法的40倍，20倍，1.6倍。随着速度模糊数的增加，由图9(c)可知，4种算法计算量随之增大，由图9(d)可知，速度模糊数超过10后，4种算法计算量增加的速度基本相同，此时基于Radon-Fourier变换，Keystone变换，Chirp Z变换积累算法的计算量约为本文算法的60倍，30倍，1.5倍。由此可见，利用本文算法实现积累所需的计算量远小于基于Radon- Fourier变换和Keystone变换的积累算法，约为基于Chirp Z变换积累算法计算量的60%。

6 结束语

本文提出了一种在快时间频域实现相参积累的快速算法，该算法基于非均匀FFT，所需运算量较小，约为Chirp Z变换的60%，远小于Keystone变换和Radon-Fourier变换。而且该算法可避免因脉冲采样起始点相对位置不同造成的积累损失，其积累性能与Chirp Z变换相同，接近相参积累的理论值，优于Keystone变换和采样率不高时的Radon- Fourier变换。

图9 几种相参积累算法运算量对比

[1] 杨建宇. 雷达技术发展规律和宏观趋势分析[J]. 雷达学报, 2012, 1(1): 19-27.

Yang Jian-yu. Development laws and macro trends analysis of radar technology[J]., 2012, 1(1): 19-27.

[2] 李品, 周海峰, 张飙. 基于距离分段的目标长时间积累方法研究[J]. 现代雷达, 2012, 34(7): 20-24.

Li Pin, Zhou Hai-feng, and Zhang Biao. A study on long-term integration based on segmented range[J]., 2012, 34(7): 20-24.

[3] 李春林, 吴琳拥. 基于Keystone变换的长时间相参积累研究[J]. 电子科技, 2013, 26(6): 148-152.

Li Chun-lin and Wu Lin-yong. Study and simulation of long-time coherent integration with Keystone transform[J]., 2013, 26(6): 148-152.

[4] 王俊, 张守宏. 微弱目标积累检测的包络移动补偿方法[J]. 电子学报, 2000, 28(12): 56-59.

Wang Jun and Zhang Shou-hong. Study on the motion compensation of range migration for weak moving target detection[J]., 2000, 28(12): 56-59.

[5] Carlson B D, Evans E D, and Wilson S L. Search radar detection and track with the Hough transform (I): system concept[J]., 1994, 30(1): 102-108.

[6] Carlson B D, Evans E D, and Wilson S L. Search radar detection and track with the Hough transform (II): detection statistics[J]., 1994, 30(1): 109-115.

[7] Carlson B D, Evans E D, and Wilson S L. Search radar detection and track with the Hough transform (III): detection performance with binary integration[J]., 1994, 30(1): 116-125.

[8] Mo L, Wu S L, and Li H. Radar detection of range migrated weak target through long-term integration[J]., 2003, 12(4): 539-544.

[9] 吴兆平, 吴惠阳, 苏涛. 距离-多普勒-时间三维雷达数据中的目标能量积累[J]. 系统工程与电子技术, 2013, 35(1): 68-72.

Wu Zhao-ping, Wu Hui-yang, and Su Tao. Integration of target energy in 3-D radar data of range-doppler-time[J]., 2013, 35(1): 68-72.

[10] Deng Feng-sen and Wang Xue-gang. Coherent integration detection algorithm research of space debris[C]. Proceedings of CIE'06 International Conference on Radar, Shanghai, 2006: 1-4.

[11] Zhang S S and Zeng T. Dim target detection based on Keystone transform[C]. Proceedings of IEEE International Radar Conference, Alington, 2005: 889-894.

[12] Xu Jia, Yu Ji, and Peng Ying-ning. Radon-Fourier transform for radar target detection (I): generalized doppler filter bank[J]., 2011, 47(2): 1186-1202.

[13] 吴兆平, 符渭波, 苏涛. 基于快速Radon-Fourier变换的雷达高速目标检测[J]. 电子与信息学报, 2012, 34(8): 1866-1871.

Wu Zhao-ping, Fu Wei-bo, and Su Tao. High speed radar target detection based on fast Radon-Fourier transform[J].&, 2012, 34(8): 1866-1871.

[14] Yu Ji, Xu Jia, and Peng Ying-ning. Radon-Fourier transform for radar target detection (III): optimality and fast implementations[J]., 2012, 48(2): 991-1004.

[15] Perry R P, DiPietro R C, and Fante R L. SAR imaging of moving targets[J]., 1994, 35(1): 188-200.

[16] Karsten F. Non-equispaced fast Fourier transforms with applications to tomography[J]., 2003, 9(5): 431-450.

田 超： 男，1987年生，博士生，研究方向为雷达总体技术与信号处理.

文树梁： 男，1971年生，博士，研究员，研究方向为雷达总体技术与信号处理.

A Long-term Coherent Integration Algorithm Based onNon-uniform Fast Fourier Transform

Tian Chao Wen Shu-liang

(23,100854,)

Sampling may cause some loss for coherent integration in time domain and the computation burdens of the common coherent integration algorithms are usually heavy. To resolve these issues, a fast algorithm realizing long-term coherent integration in fast-time frequency domain is proposed. The algorithm firstly utilizes non-uniform FFT to accomplish range walk correction and phase compensation in fast-time frequency domain, and then fulfills the integration via IFFT. The proposed algorithm can avoid loss entailed by sampling, and needs relatively less computation. The theoretical analysis and simulation results demonstrate the effectiveness of the proposed algorithm.

Radar signal processing; Long-term coherent integration; Non-uniform FFT; Motion compensation

TN957.51

A

1009-5896(2014)06-1374-07

10.3724/SP.J.1146.2013.01264

田超 qctchao87@126.com

2013-08-20收到，2013-11-27改回