凝汽式汽轮机级组当量喷嘴通流面积计算方法及其应用*
2014-05-30吴智刚曹丽华
李 勇 吴智刚 曹丽华
(东北电力大学能源与动力工程学院)
汽轮机通流部分故障是火力发电厂主要故障之一,常见的故障种类有叶片腐蚀、结垢、断裂及损坏等。这些故障的发生总会引起热力参数的变化,因而可通过监测机组热力参数来诊断通流部分故障。汽轮机通流部分是其最重要的核心部分,研究通流部分故障机理和诊断方法,对维护机组安全、经济运行具有重要意义[1~4]。
在汽轮机通流部分结垢程度监测与诊断方面,文献[5]通过仿真研究,揭示了通流部分结垢对汽轮机安全经济性影响的原因。文献[6]采用监测汽轮机监视段压力是否超过其应达值的10%来判断通流部分结垢情况,但监视段测点离结垢的级越远,监视段压力对结垢的敏感程度就越小。文献[7]提出一种计算汽轮机通流部分结垢厚度的方法,但该方法需要预先确定各级结垢厚度比例系数,而在汽轮机实际运行中,准确确定各级结垢厚度比例系数难以实现。文献[8]建立了汽轮机通流部分结垢与热力状态参数的关系,并给出了判别汽轮机通流部分结垢程度的神经网络模型,但其需预先确定各级结垢厚度比例系数和结垢平均厚度,这些数据在汽轮机运行过程中很难准确确定。文献[9]给出了凝汽式汽轮机通流部分结垢诊断方法,虽对汽轮机通流部分结垢进行定性分析,但没有定量诊断。文献[10]提出了基于弗留格尔公式的汽轮机特征通流面积的概念,以反映汽轮机通流面积的变化情况,但其在汽轮机负荷变化时,特征通流面积也发生较大的变化,影响到对汽轮机通流部分状态的诊断精度。
为此,笔者从汽轮机通流部分故障监测与诊断的实际需求出发,提出了一种汽轮机级组在亚临界和临界流动状态下当量喷嘴通流面积的概念,并对其变工况特性进行了分析,结果表明级组的当量喷嘴通流面积可以反映汽轮机通流部分面积的变化情况,并在某300MW汽轮机通流部分状态诊断中得到了应用。
1 级的当量喷嘴通流面积
1.1 级的当量假想速度
文献[11]指出,假想整个级的滞止理想焓降都在当量喷嘴中等熵膨胀进行,则此时这个当量喷嘴的出口速度就称为级的假想速度,即:
(1)
式中ca——假想全级滞止理想比焓降都在喷嘴中等熵膨胀的假想出口速度,m/s;

笔者参照假想速度的概念,提出了级的当量假想速度,即假想整个级的有效比焓降都在当量喷嘴中膨胀进行,则此时这个当量喷嘴的出口速度就称为级的当量假想速度,即:
(2)
式中cen——假想全级比焓降都在当量喷嘴中膨胀的当量假想出口速度,m/s;
Δhi——蒸汽在级中的实际比焓降,kJ/kg。
1.2 级的当量喷嘴通流面积表达式
级的当量喷嘴通流面积是指将汽轮机的一个级假定为一个喷嘴,用该喷嘴的通流面积表征级的通流面积,此时的喷嘴面积即为级的当量喷嘴通流面积。此时级的前后压比也就是当量喷嘴的前后压比。
当采用当量喷嘴来表示一个级时,由于级的临界状态与喷嘴临界状态的临界压比不同,对于一个亚临界流动的级,当量喷嘴内可能是亚临界也可能达到超临界流动状态。因此,分别对其进行讨论。
当级内为亚临界,当量喷嘴内亦为亚临界流动时,由汽轮机原理知,隔板漏气量为[12]:
(3)
式中Aδ——喷嘴的隔板间隙,m2;
c1——喷嘴出口汽流的绝对速度,m/s;
Gδ——喷嘴的隔板漏气量,kg/s;
v1——喷嘴出口蒸汽比容,m3/kg。
级内喷嘴的流量为:
(4)
式中An——喷嘴出口截面积,m2;
G——流过该级的流量,kg/s。
由连续性方程,有:
(5)
式中A——级的当量喷嘴通流面积,m2;
v2——动叶出口蒸汽比容,m3/kg。
由式(5)得:
(6)
其中:
(7)
式中 Δhn——蒸汽在喷嘴中的比焓降,kJ/kg。
当量喷嘴在亚临界状态下级的简化热力过程线如图1所示。

图1 当量喷嘴在亚临界状态下级的简化热力过程线
另外,近似认为各等压线互相平行,则:
(8)
式中 Δht——蒸汽在级中的理想比焓降,kJ/kg;
Δhnt——蒸汽在喷嘴中的理想比焓降,kJ/kg;
Ωm——级的反动度。
将式(8)代入式(7),得:
(9)
另外,由图1可以看出[13]:
(10)
式中k——绝热系数;
p1——喷嘴后蒸汽压力,MPa;
p2——动叶后蒸汽压力,MPa;
n——多变指数;
η——级或级组相对内效率。
近似取压力反动度等于焓降反动度,即:
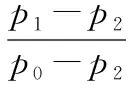
(11)
(12)
式中p0——级前压力,MPa。
将式(12)代入式(10),得:
(13)
式中ε——级的前后压比,ε=p2/p0。
将式(9)、(13)代入式(6),即可得到表征级内为亚临界流动,当量喷嘴亦为亚临界流动时级的当量喷嘴通流面积的表达式,即:
(14)
当级内为亚临界,当量喷嘴内达到超临界流动时,由连续性方程可知:
(15)
式中ccr——蒸汽在当量喷嘴中达临界状态时的速度,m/s;
vcr——蒸汽在当量喷嘴中达临界状态时对应的比容,m3/kg。
由式(15)得:
(16)
其中:
(17)
式中 Δhcr——蒸汽在当量喷嘴中达临界状态时的实际比焓降,kJ/kg。
当量喷嘴在临界状态下级的简化热力过程线如图2所示。
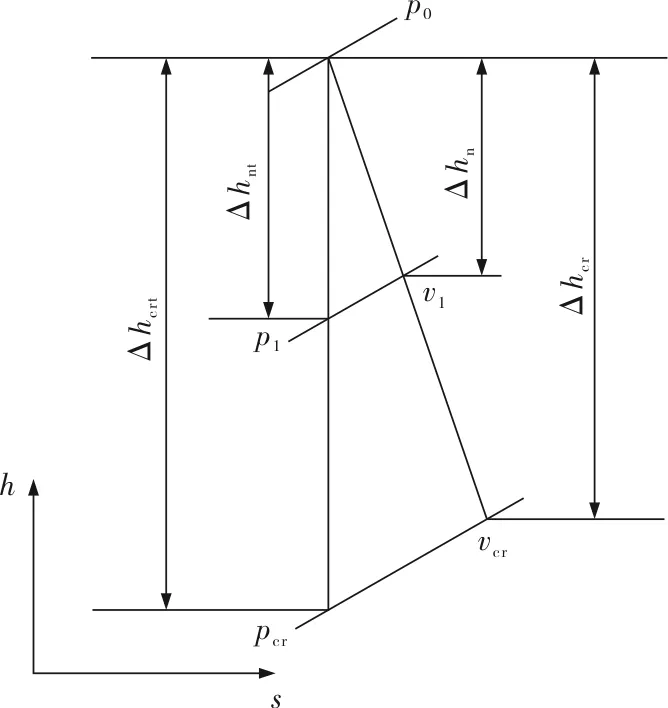
图2 当量喷嘴在临界状态下级的简化热力过程线
类似于式(7)有:
(18)
另外,由图2可以看出:
(19)
(20)

(21)
式中pcr——蒸汽在当量喷嘴内流动达临界状态时的压力,MPa;
εcr——蒸汽在当量喷嘴内流动达临界状态时的压比。
将式(20)、(21)代入式(19),得:
(22)
将式(18)、(22)代入式(16),即可得到表征级内为亚临界流动,当量喷嘴为超临界流动时级的当量喷嘴通流面积的表达式,即:
(23)
由式(14)、(23)可以看出,级的当量喷嘴通流面积除了与本级喷嘴出口截面积有关外,还取决于该级的前后压比和反动度。而由汽轮机原理可知[12],对于凝汽式汽轮机的中间某级,只要通流部分状态正常,只有负荷变化时,在较大的负荷变化范围内,中间各级的反动度、压比和多变指数基本保持不变。因此,级的当量喷嘴通流面积可以反映级的通流面积的大小。
2 级组的当量喷嘴通流面积
2.1 级组的当量喷嘴通流面积表达式
级组的当量喷嘴通流面积是指将汽轮机的一个级组假定为一个喷嘴,用该喷嘴的面积表征级组的面积,此时的喷嘴面积即为级组的当量喷嘴通流面积。
笔者主要讨论级组内各级均为亚临界工况时的当量喷嘴通流面积。另外,级组内各级为亚临界流动,其对应的当量喷嘴内可能是超临界流动,也可能是亚临界流动。下面,分别对其进行讨论。
当级组和当量喷嘴内均为亚临界流动时,对于由两个级组成的级组,当量喷嘴前后压比大于临界压比时,由连续性方程知:
(24)
(25)
式中As——级组的当量喷嘴通流面积,m2;
An1——级组内第一级喷嘴出口截面积,m2;
Aδ1——级组内第一级喷嘴的隔板间隙,m2;
c11——级组内第一级喷嘴出口汽流的绝对速度,m/s;
cens——假想全级组比焓降都在当量喷嘴中膨胀的假想出口速度,m/s;
v11——级组内第一级喷嘴出口蒸汽比容,m3/kg;
v22——级组内第二级动叶出口蒸汽比容,m3/kg。
笔者分别讨论式(25)中各项的计算方法,对于比容项,有:
(26)
式中p11——级组内第一级喷嘴后蒸汽压力,MPa;
p21——级组内第一级动叶后蒸汽压力,MPa;
p22——级组内第二级动叶后蒸汽压力,MPa;
ε1——级组内第一级的压比;
ε2——级组内第二级的前后压比;
Ωm1——级组内第一级的反动度。
对于式(26)中的速度项,有:
(27)
式中 ΔHi——级组内蒸汽的实际比焓降,kJ/kg;
p0s——级组前压力,MPa;
R——蒸汽的气体常数,kJ/(kg·K);
T0——级组前温度,K。
当量喷嘴在亚临界状态下级组的简化热力过程线如图3所示,其中Δhni1为第一级喷嘴内蒸汽的实际焓降,单位kJ/kg。

图3 当量喷嘴在亚临界状态下级组的简化热力过程线
化简式(27)得:
(28)
将式(26)、(28)代入式(25)得:
(29)
以此类推,当级组中有N级时,则:
(30)
式中εi——级组内各级的压比。
综合式(29)、(30)可以得到级组和当量喷嘴内均为亚临界流动时级组的当量喷嘴通流面积表达式为:
As=(An1+Aδ1)×
(31)
式中εens——级组前后压比。
当级组内为亚临界流动,而当量喷嘴内达到临界流动时,若把级组假定为一个喷嘴,级组的前后压比就是该假想喷嘴的前后压比。此时就可能出现该假想喷嘴的前后压比小于或等于临界压比的情况。对于由两个级组成的级组,当级组前后压比小于或等于临界压比时,由连续性方程知:
(32)
由式(32)得:
(33)
下面,分别讨论式(33)中各项的计算方法,对于比容项,有:
(34)
对于式(33)中的速度项,有:
(35)
式中 ΔHcr——蒸汽在当量喷嘴内膨胀到临界状态时的比焓降,kJ/kg。
当量喷嘴在临界状态下级组的简化热力过程线如图4所示,ΔHcrt为当量喷嘴内蒸汽达临界状态时蒸汽的理想比焓降,单位kJ/kg。

图4 当量喷嘴在临界状态下级组的简化热力过程线
将式(34)、(35)代入式(33)得:
(36)
以此类推,当级组中有N个级时,只要假想喷嘴的临界压力大于或等于级组蒸汽后压力,均有:
(37)
由式(31)、(37)可以看出,级组的当量喷嘴通流面积只取决于级组内第一级的反动度、第一级的前后压比、第一级的喷嘴面积和级组的前后压比。对于凝汽式汽轮机的中间各级组,级组的当量喷嘴通流面积同样可以反映级组通流面积的大小。
2.2 级组的当量喷嘴通流面积的计算式
式(31)、(37)反映了级组当量喷嘴通流面积的表达式及其影响因素。在实际应用时,由于涉及到级组中第一级的结构面积和前后压比,导致无法采用式(31)、(37)计算级组的当量喷嘴通流面积。为此,笔者给出级组当量喷嘴通流面积的计算式。
当级组和当量喷嘴内均为亚临界流动时,当量喷嘴前后压比εs>εcr,由式(24)得:
(38)
(39)
式中p2s——级组出口蒸汽压力,MPa;
v0s——级组入口蒸汽比容,m3/kg;
εs——当量喷嘴的压比。
级组的当量假想速度为:
(40)
将式(39)、(40)代入式(38),即可得到级组当量喷嘴通流面积为:
(41)
将式(41)简单变形后,得:
(42)
当级组内为亚临界流动,而当量喷嘴内达到临界流动时,当量喷嘴前后压比εs≤εcr,此时当量喷嘴的前后压比为喷嘴的临界压比,即:
(43)
将式(43)代入(41)化简得:
(44)
另外,文献[10]通过将弗留格尔公式进行简单变形,得到级组特征通流面积为:
(45)
对比式(31)、(37)、(42)和(44)可以看出,由于笔者给出的级组当量喷嘴通流面积是利用连续性方程和蒸汽在级组内的热力过程通过较严密的数学推导得到的,因而更加符合实际情况。
2.3 级组的当量喷嘴通流面积的变工况特性
2.3.1汽轮机各级组的划分
为研究级组当量喷嘴通流面积在变工况下值的变化,以某300MW汽轮机热平衡图数据进行计算分析。该汽轮机共有36级,其中高压缸有13个级(1个调节级和12个压力级),中压缸9个级,低压缸14个级(对称分流布置,每边各7个级),将除调节级外的各级按相邻抽汽点划分级组,如图5所示,图中罗马字母表示各级组的编号。因最后两级组内蒸汽可能达到临界速度,故计算时不考虑这两个级组。

图5 300MW汽轮机级组的划分
2.3.2级组的当量喷嘴通流面积值及对比
为了分析级组的当量喷嘴通流面积随负荷的变化情况,根据300MW汽轮机的热平衡图数据,得到各级组当量喷嘴通流面积值及其相对于额定工况时的偏差率的计算结果见表1。同时,为了便于对比,将采用文献[10]得到的式(45)的计算结果也一并列于表1中。

表1 300MW汽轮机不同工况下各级组当量喷嘴通流面积值、特征通流面积值及其偏差率

(续表1)
从表1可以看出:当汽轮机由额定工况变为50%额定工况时,采用式(42)、(44)计算得到的各级组当量喷嘴通流面积相对于额定工况时的偏差率最大仅为1.492 3%,各偏差率绝对值的平均值为0.274 6%;而采用文献[10]得到的特征通流面积最大偏差率达到2.050 6%,各偏差率绝对值的平均值为0.831 9%,这说明笔者计算得到的当量喷嘴通流面积受负荷影响更小,更适合于表征汽轮机的通流部分面积。
由于当量喷嘴通流面积值的大小受多变指数的影响,而多变指数与级组效率有关。为分析当通流部分面积不变,仅由表面粗糙度变化引起效率降低时,当量喷嘴通流面积的变化情况,现以第Ⅱ级组为例,计算仅当效率降低而其他因素不变时级组的当量喷嘴通流面积,结果如图6所示。

图6 第Ⅱ级组效率降低时当量喷嘴通流面积
从图6可以看出,当第Ⅱ级组效率由大修后的91.5%降到88.5%时,其对应的当量喷嘴通流面积从0.032 85m2变到0.033 37m2,其最大偏差率为1.570 0%,在2%之内。由此说明,该方法不会将叶片表面粗糙度变化误诊断为通流部分面积变化。
综上所述,在实际运行过程中,当汽轮机通流部分正常时,当量喷嘴通流面积几乎不随工况和热力参数的变化而变化;但当汽轮机通流部分出现结垢时,当量喷嘴通流面积会发生变化。因此,通过对级组当量喷嘴通流面积的在线监测,并与通流部分状态正常时的当量喷嘴通流面积进行对比,即可实现对汽轮机通流部分状态的监测与诊断。
3 当量喷嘴通流面积在汽轮机通流部分诊断中的应用
某300MW汽轮机运行中出现性能下降,出力不足,低压缸效率下降的状况。为了诊断汽轮机性能降低原因,对其进行通流部分状态诊断。
该汽轮机各个级组的当量喷嘴通流面积正常值通过汽轮机大修后运行数据计算获得,当量喷嘴通流面积运行值通过监测系统在线监测计算获得。各个级组的当量喷嘴通流面积运行值的平均值和相应的偏差率见表2。考虑到参数的测量误差等因素,当量喷嘴通流面积相对于正常值偏差率达到-2%时认为级组通流部分结垢;当量喷嘴通流面积相对于正常值偏差率达到+2%时认为级组通流部分间隙增大或腐蚀。
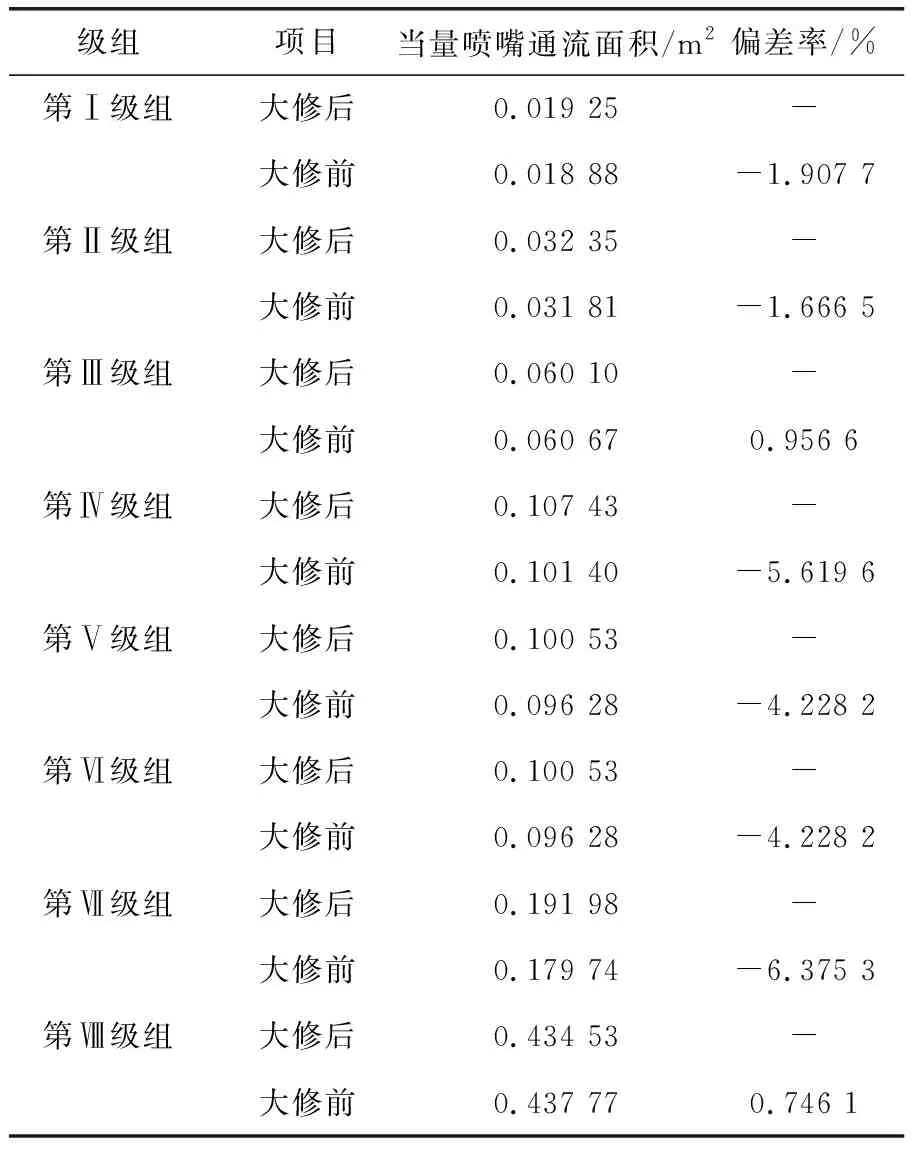
表2 300MW汽轮机大修前后当量喷嘴通流面积值及其偏差率
从表2可知,前3个级组和第Ⅷ级组的当量喷嘴通流面积值的偏差率的绝对值在2%以内,说明这4个级组通流部分状态正常。第Ⅳ、Ⅴ、Ⅵ、Ⅶ级组的当量喷嘴通流面积值的偏差率都为负值,且绝对值大于2%,诊断结论为这4个级组通流部分结垢,这与开缸大修后所得通流部分故障结论相吻合,验证了该方法的可行性。
以另一300MW汽轮机为例计算大修前后各级组当量喷嘴通流面积,结果发现第Ⅷ级组通流部分异常,如图7所示。

图7 第Ⅷ级组大修前后当量喷嘴通流面积值
从图7可以看出,大修前第Ⅷ级组当量喷嘴通流面积值与大修后相比显著偏大,其偏差率的平均值为2.530 0%,说明该级组通流部分间隙变大,这同样与开缸大修后所得通流部分故障结论相吻合。
4 结论
4.1笔者给出了级和级组当量喷嘴通流面积的表达式和计算式,通过对某300MW汽轮机不同工况下级组当量喷嘴通流面积的计算,结果表明在汽轮机通流部分状态正常时,不同工况下级组当量喷嘴通流面积的偏差值很小,当量喷嘴通流面积可以作为反映级组通流面积的当量参数。
4.2通过将汽轮机运行时的当量喷嘴通流面积与通流部分状态正常时的当量喷嘴通流面积进行对比,可以对汽轮机级组通流部分状态进行诊断。
4.3通过对某300MW机组实际案例进行诊断,所得结论与开缸大修所得的故障结论相同,证明了该方法的可行性。
[1] 周云龙,曹丽华,徐伟,等.汽轮机通流部分间隙变化对相对内效率和功率的影响[J].热力发电,2010,39(3):90~92.
[2] 孙凯,田国清,田宏,等.基于IGA-SVM的汽轮机故障诊断研究[J].东北电力大学学报,2012,32(3):26~30.
[3] 董晓峰,顾煜炯,杨昆,等.汽轮机通流部分故障诊断方法研究[J].中国电机工程学报,2010,30(35):71~77.
[4] 栾忠兴,李勇,薛彦光,等.汽轮机静叶栅二次流损失的数值研究[J].东北电力大学学报,2012,32(3):43~47.
[5] Kubiak J A,Gustavo U B.Simulation of the Effect of Scale Deposition on a Geothermal Turbine[J].Geothermics,2002,31(5):545~562.
[6] (苏)卡别洛维奇.汽轮机设备运行[M].北京:水利电力出版社,1988:56~89.
[7] 王一兵,高洪涛.汽轮机叶片结垢厚度的理论计算[J].汽轮机技术,1998,40(5):286~287.
[8] 高洪涛,黄钟岳.汽轮机叶片结垢在线诊断的一种新方法[J].大连理工大学学报,1999,39(4):538~541.
[9] 李勇,徐君诏,黄萍力.凝汽式汽轮机通流部分结垢诊断方法研究[J].汽轮机技术,2008,50(5):371~373.
[10] 徐大懋,邓德兵,王世勇,等.汽轮机的特征通流面积及弗留格尔公式改进[J].动力工程学报,2010,30(7):473~477.
[11] 吴承雄.涡轮机当量喷嘴截面积的计算方法[J].华中工学院学报,1984,12(1):93~97.
[12] 沈士一.汽轮机原理[M].北京:中国电力出版社,1998:1~143.
[13] 曹祖庆.汽轮机变工况特性[M].北京:水利水电出版社,1991:1~12.
