一种投票式并行RANSAC算法及其FPGA实现
2014-05-30凌思睿
江 洁 凌思睿
一种投票式并行RANSAC算法及其FPGA实现
江 洁 凌思睿*
(北京航空航天大学精密光机电一体化技术教育部重点实验室 北京 100191)
随机抽样一致(RANdom SAmple Consensus, RANSAC)算法在数据量大,局外点比例高,模型复杂等情况下运算速度明显下降。该文提出一种投票式并行RANSAC算法,在把假设阶段并行化,同时生成多个模型的基础上,提出多个模型并行对同一个数据点投票,直接判断其是否属于局内点的方法,省去了传统方法中根据最佳模型重新筛选数据点的步骤。在以FPGA为代表的并行平台上,该算法可以充分利用其硬件资源和并行处理特性,实现深度流水线的并行运算。实验结果表明该算法不仅拥有更好的鲁棒性,其性能和数据吞吐量还获得了大幅提升。
FPGA;随机抽样一致(RANSAC);并行计算
1 引言
Fischler等人[1]在1981年提出的RANSAC(RANdom SAmple Consensus)算法,由于其原理简单,鲁棒性强,目前已广泛应用于含错误数据的模型估计,如目标检测,立体图像匹配等。

提高RANSAC性能的另一种方法是并行化。如袁红星等人[13]和Lee等人[14]等提出利用GPU并行计算RANSAC中的多个“假设-检验”过程;Fijany等人实现了在ClearSpeed[15]和Tilera[16]平台上的多数据流RANSAC算法。这些并行化方法虽然达到了加速的效果,但某些地方还存在速度瓶颈,依赖于计算机平台且功耗较大,应用场合受到限制。
本文在把RANSAC算法深度并行化的基础上,提出一种投票式数据检验方法,提高了RANSAC算法的性能和数据吞吐量。本文还以圆的提取为例,利用FPGA的并行处理特性和丰富的资源实现了该算法,能满足高速实时处理的需求。
2 传统RANSAC算法
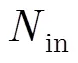

两边取对数得
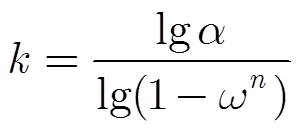
3 并行RANSAC算法及其FPGA实现
串行RANSAC算法要求对“假设-检验”过程进行次迭代,导致计算速度难以提高;常见的并行化方案只是简单地把原串行方案分成多个线程同时执行,寻找最佳模型时依然需要串行操作,影响了整体速度。本文提出了一种投票式并行RANSAC算法,通过把假设阶段并行化以及对数据点并行投票,直接检验,获得了可观的性能提升。
3.1 假设阶段的并行化

3.2 投票式检验
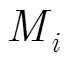

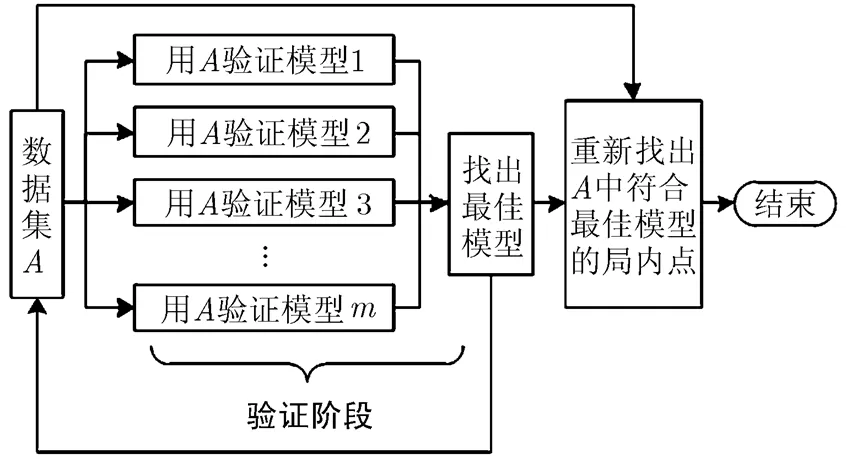
图1 现有并行检验方法流程图
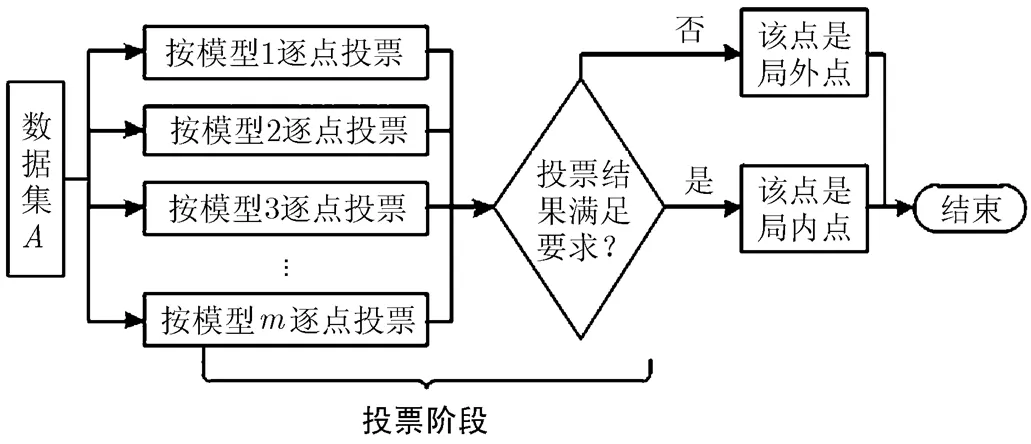
图2 本文投票检验方法流程图
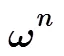

3.3 并行RANSAC算法的FPGA实现
以提取圆为例,投票式并行RANSAC算法在FPGA上的实现方法如下。
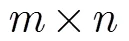
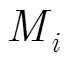

图3 随机采样与并行假设模块

图4 圆模型的假设模块内部结构(3点定圆)
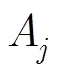
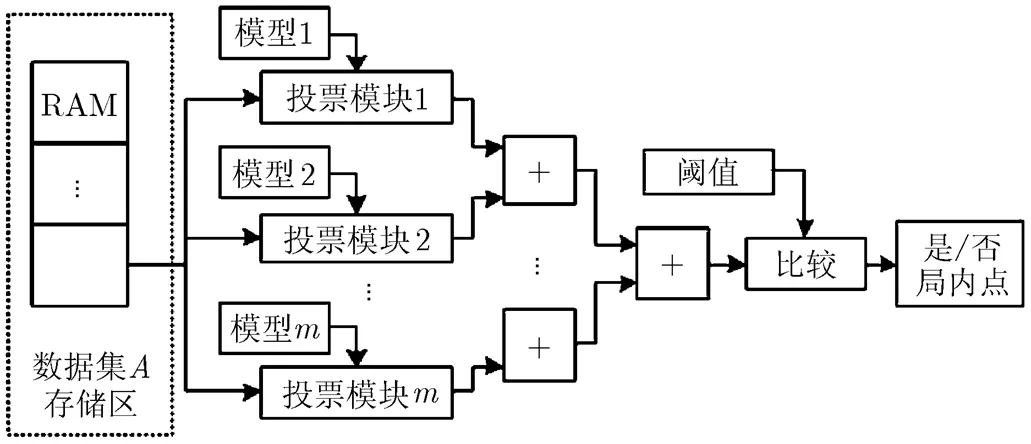
图5投票检验模块
4 性能评估与实验
4.1 算法性能评估
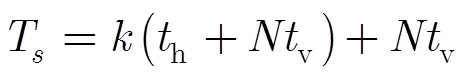

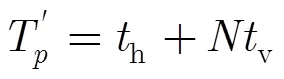

表2 RANSAC算法性能比较
本文算法除上述的性能优势外,还利用FPGA充足的硬件资源和高度的并行性,实现了多指令多数据流的深度流水线运算,避免了寻找最佳模型时的串行操作,基本消除了RANSAC算法在数据吞吐量上的瓶颈。
4.2 仿真实验
仿真实验目的是比较PC上的传统RANSAC与FPGA上的并行RANSAC的准确性和运算速度。实验环境:CPU为Intel Core2 Duo E7400的PC平台;XILINX公司Virtex-5 LX330 FPGA。为了测试不同样本错误率和样本大小下两种RANSAC算法的特性,设计了估计圆的仿真实验,真实圆心为(600,450),半径为300。数据集大小分别为1000, 10000, 100000, 1000000,局外点呈2维均匀分布,比例分别为10%, 20%, 30%, 40%, 50%。在置信水平99%的条件下求解。
在不同的局外点比例下各进行100次试验,统计其正确结果和错误结果的个数,表3和图7为两种算法的准确性比较。可以看出,传统算法找到的正确局内点比例稳定在98.5%附近,本文算法的漏检率全面优于传统算法。更重要的是,本文算法给出的错误结果明显少于传统算法,说明本文算法的鲁棒性得到了提高。

图7 两种RANSAC算法找到的正确局内点比例
表4为两种RANSAC算法的运算速度比较。实验结果显示,当样本数量和局外点比例较小时,并行RANSAC的性能优势不很明显;而样本数据量大,局外点比例高时,并行RANSAC时间复杂度小的特点得到了很好的体现。如当=1000000,=50%时,即使CPU的运行频率(2.8 GHz)是FPGA(100 MHz)的28倍,并行RANSAC的运算速度仍然达到了传统算法的56倍。此外,在实际应用中常见数据集大小相近而噪声等干扰数量随机波动的情况,而并行RANSAC耗费的时间与局外点比例无关,很好地保证了算法的实时性。
4.3 真实图像处理实验
在天文导航中,需要用图像处理的方法提取近天体目标(如地球、月球)的中心。相机拍摄到的地球图像(图8(a))经过边缘提取获得含有干扰的圆图像(图8(b))后,可以利用RANSAC算法去除干扰,再用最小二乘法拟合圆心(图8(c))。
表3两种RANSAC算法在不同局外点比例下的准确性

局外点比例(%) 1020304050 实际局内点9998960088880000777696006666000055550000 正确结果传统9913007788427854758474716567091553908040 本文9998960088872968769644986634127455111747 错误结果传统768862187130333199 本文000115
表4两种RANSAC算法在不同数据集大小和局外点比例下的耗时(ms)

数据集大小局外点比例(%) 1020304050 传统本文传统本文传统本文传统本文传统本文 1000 0.12960.01126 0.11100.01126 0.1812 0.01126 0.3006 0.01126 0.5742 0.01126 10000 0.63130.10130 1.78670.10130 1.7747 0.10130 3.7239 0.10130 5.5898 0.10130 100000 6.35421.0013011.18241.0013030.8633 1.00130 30.5217 1.00130 62.6235 1.00130 100000063.648010.00100113.123010.00100179.089010.00100308.515010.00100566.284010.00100

图8 天体目标圆心提取示意图
用FPGA和PC对含干扰的地球图像(图8(a))进行圆心提取,结果如表5所示。

表5 FPGA圆心提取结果
FPGA提取的圆心与软件计算结果基本一致。在Virtex-5 LX330 FPGA上综合、布局布线后,并行RANSAC模块(其中包含30个假设模块和投票模块)占用60个硬核DSP模块,81780个LUTs和66750个寄存器。整个圆心提取系统在100 MHz的时钟下,图像输入完毕后经过2.063 ms可获得圆心和半径的拟合结果(边缘点约为1400个,局外点比例10%),可以获得最高484.7帧/s的处理速度。
5 结论
本文提出了一种改进的并行RANSAC算法,首先把假设阶段并行化,同时生成多个模型,之后采用投票方式对数据点进行检验,直接从数据集中获得局内点,与现有并行算法相比节省了一半时间。模拟数据和真实图像处理结果表明,该并行算法在改善RANSAC鲁棒性的同时有效提高了其性能。在大样本、高局外点比例的情况下,该算法能充分利用FPGA硬件的并行特性,在准确度和速度上均有更好的表现。
[1] Fischler M A and Bolles R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]., 1981, 24(6): 381-395.
[2] 陈付幸, 王润生. 一种新的消失点检测算法[J]. 电子与信息学报, 2008, 28(8): 1458-1462.
Chen Fu-xing and Wang Run-sheng. A new vanishing point detecting algorithm[J].&, 2008, 28(8): 1458-1462.
[3] Priyadarshi Bhattacharya and Marina Gavrilova. Improving RANSAC feature matching with local topological information[C]. 2012 Ninth International Symposium on Voronoi Diagrams in Science and Engineering, Piscataway, 2012: 17-23.
[4] Baker C L and Hoff W. DIRSAC: a directed sampling and consensus approach to quasi-degenerate data fitting [C]. 2013 IEEE Workshop on Applications of Computer Vision, Clearwater Beach, 2013: 154-159.
[5] El-Melegy M T. RANSAC algorithm with sequential probability ratio test for robust training of feed-forward neural networks[C]. Proceedings of International Joint Conference on Neural Networks, San Jose, 2011: 3256-3263.
[6] 周骏, 陈雷霆, 刘启和, 等. 基于序贯概率及局部优化随机抽样一致性算法[J]. 仪器仪表学报, 2012, 33(9): 2037-2044.
Zhou Jun, Chen Lei-ting, Liu Qi-he,Fast and accurate RANSAC based on optimal sequential probability test and local optimization[J]., 2012, 33(9): 2037-2044.
[7] Golban C, Szakats I, and Nedevschi S. Stereo based visual odometry in difficult traffic scenes[C]. 2012 Intelligent Vehicles Symposium, Alcalá de Henares, 2012: 736-741.
[8] 张文聪, 李斌, 邓宏平, 等. 视线跟踪过程中变形瞳孔的定位[J]. 电子与信息学报, 2010, 32(2): 416-421.
Zhang Wen-cong, Li Bin, Deng Hong-ping,Distorted pupil localization in eye tracking[J].&, 2010, 32(2): 416-421.
[9] Xu M and Lu J. Distributed RANSAC for the robust estimation of three-dimensional reconstruction[J]., 2012, 6(4): 324-333.
[10] Martelli S, Marzotto R, Colombari A,FPGA-based robust ellipse estimation for circular road sign detection[C]. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), San Francisco, 2010: 53-60.
[11] Marzotto R, Zoratti P, Bagni D,A real-time versatile roadway path extraction and tracking on an FPGA platform[J]., 2010, 114(11): 1164-1179.
[12] Dohi K, Hatanaka Y, Negi K,Deep-pipelined FPGA implementation of ellipse estimation for eye tracking[C]. 2012 22nd International Conference on Field Programmable Logic and Applications (FPL), Oslo, 2012: 458-463.
[13] 袁红星, 吴少群, 朱仁祥, 等. 平面单应性矩阵求解的CUDA 并行实现[J]. 微型机与应用, 2012, 31(23): 38-41.
Yuan Hong-xing, Wu Shao-qun, Zhu Ren-xiang,CUDA-based parallel implementation of homography estimation[J].&, 2012, 31(23): 38-41.
[14] Lee Dong-hwa, Kim Hyong-jin, and Myung Hyun. GPU- based real-time RGB-D 3D SLAM[C]. 2012 9th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Daejeon, 2012: 46-48.
[15] Fijany A and Hosseini F. Image processing applications on a low power highly parallel SIMD architecture[C]. IEEE Aerospace Conference, Big Sky, 2011.
[16] Fijany A and Diotalevi F. A cooperative search algorithm for highly parallel implementation of RANSAC for model estimation on Tilera MIMD architecture[C]. IEEE Aerospace Conference, Big Sky, 2012.
[17] 孙红伟. 二项分布两种近似计算的讨论[J]. 河南教育学院学报(自然科学版), 2007, 16(1): 28-29.
Sun Hong-wei. Discussion about two approximate calculations of binomial distribution[J].(), 2007, 16(1): 28-29.
江 洁: 女,1973年生,教授,博士生导师,研究方向为实时图像处理和天体敏感器技术.
凌思睿: 男,1988年生,硕士生,研究方向为实时图像处理和天体敏感器技术.
Parallel Voting RANSAC and Its Implementation on FPGA
Jiang Jie Ling Si-rui
(-,,,100191,)
RANdom SAmple Consensus (RANSAC) performs poor with the mass of data, high outliers ratio and complicated models.In this paper, a highly parallel voting version of RANSAC is presented. On the basis of parallelizing the hypothetical stage and generating multiple models simultaneously, a novel strategy of voting to determine whether a point belongs to inliers is proposed. Conventional search for the inliers relative to the best model is saved. On parallel platforms represented by FPGA, this algorithm can take advantage of the parallel architecture and characteristics to achieve deep-pipelined parallel computing. Experiments demonstrate the good robustness of the proposed algorithm and its considerable improvement of both speed and throughput.
FPGA; RANdom SAmple Consensus (RANSAC); Parallel computing
TP391
A
1009-5896(2014)05-1145-06
10.3724/SP.J.1146.2013.00962
凌思睿 lingsirui@126.com
2013-07-04收到,2013-11-08改回
国家自然科学基金(61222304)和高等学校博士学科点专项科研基金(20121102110032)资助课题
