管壳式换热器分段模拟数值方法的适应性研究

郭崇志 陈孝文

(华南理工大学)

研究固定管板换热器的温差应力对提高设备可靠性、延长设备使用寿命意义重大[1～3]。但由于设备结构和流道的复杂性，要获取具有足够精度的数值分析结果，必须采用数值模拟方法[4，5]。文献[6，7]提出了分段模拟、整体综合的核心思想和原理，并运用此方法实现了三维实体换热器模拟研究。文献[8]用该方法研究了预应力换热器最佳预变形，并进行了实验验证。为探讨传统整体建模分析法与分段模拟法的适应性，分别利用分段模拟和整体模拟技术进行了相同流动与传热条件的分析对比。研究发现，分段模拟技术几乎不受换热器尺度及离散化精度的限制，而整体模型往往有较大的限制，尺度稍有增大便会导致计算失效。由此证明分段模拟技术对于实际工程规模计算具有良好的适应性。

1 计算模型

所研究换热器的主体结构由彼此之间相互约束的元件构成。为重点比较壳程流动与传热，选择简化管程流体行为，即假定管程为潜热释放过程。为提高计算精度，减少网格数量，适合整体建模和分段建模，采用整体模型分割离散实现网格分块。结构参数如下：

管心距Pt19mm

管板厚度δ12mm

导流筒外径×厚度×长度φ92mm×1mm×120mm

折流栅尺寸φ100mm×5.5mm×6mm

壳体φ115mm×6.5mm×1476mm

换热管 19-φ12mm×3mm×1500mm

折流杆直径Dr3mm

折流板间距B50mm

物性参数如下：

密度 7 840kg/m3

热膨胀系数 11.6×10-61/K

泊松比 0.3

导热系数 47.5W/(m·℃)

弹性模量 210GPa

比热 502.48J /(kg·K)

整体模型结构如图1所示，图2、3分别给出整体CFD模型和ANSYS模型，图4、5给出了相应的分段模型。

图1 换热器整体模型示意图

图2 CFD整体实体模型

图3 ANSYS整体几何模型

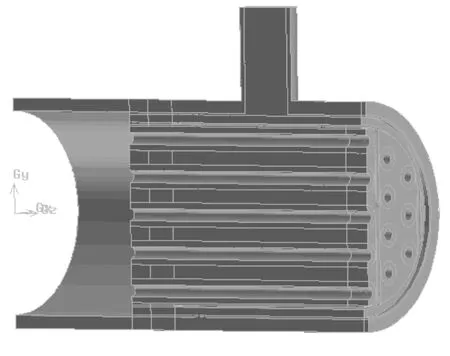
图4 换热器分段进口模型

图5 换热器分段折流栅段模型

2 CFD模拟结果

图6给出了整体模型和相应分段模型计算结果云图对比，可以看出，相同工艺参数下，整体模型和分段模型换热器的温度分布几乎看不出差异。笔者通过改变管程流体温度来获得不同的壳程流体出口温度，从而考察管程工艺条件改变情况下，两种模拟方法所产生的壳程出口温度差异(表1)。从表1可以看出，出口温度偏差最大仅为0.655 5%。说明在相同工艺条件下，分段模型和整体模型计算精算没有差别。

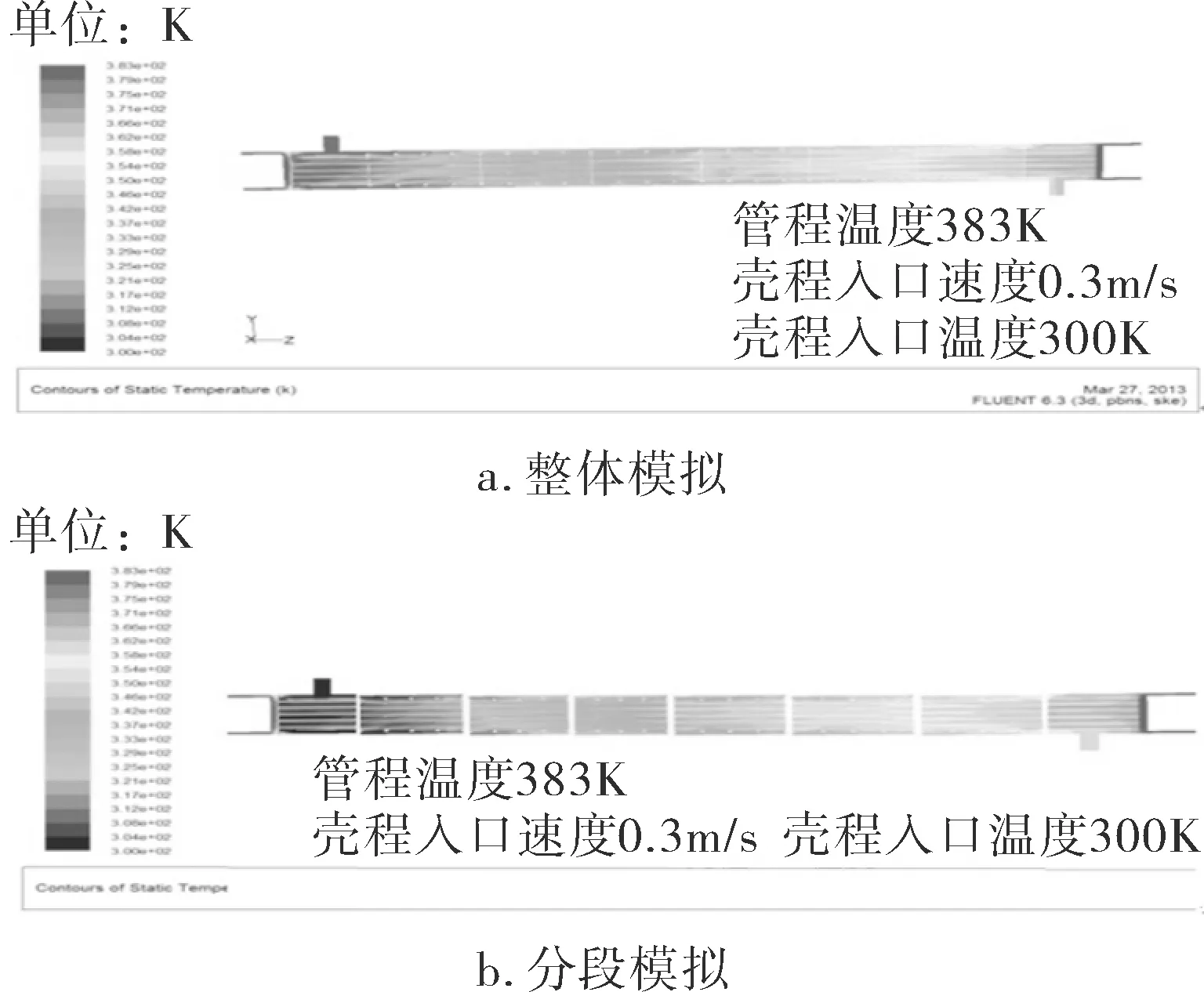
图6 两种模拟方法下的温度分布云图

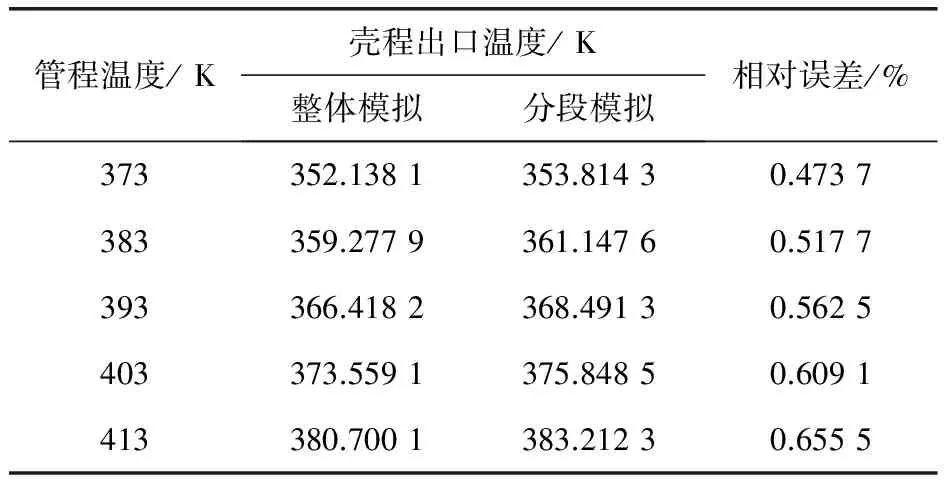
表1 两种模拟方法壳程出口温度对比

为了解分段数目对模拟结果的影响，将相同的换热器分成不同段数，将不同管程温度下的各分段结果与整体模拟结果对比，相对误差见表2。

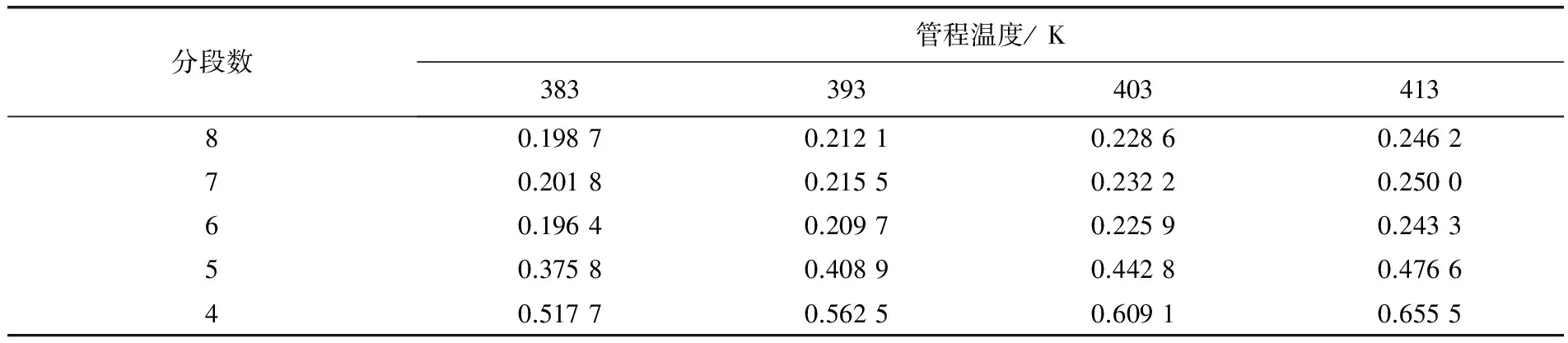
表2 各管程温度情况下分段与整体方法的相对误差 %

由表2可见，随分段数的增加，整体模拟与分段模拟相比较，壳程流体出口温度的相对误差趋于下降。最大偏差仅为0.655 5%，这说明分段数目对两种模拟方法获得的模拟结果影响不大。

3 结构温度场

利用面插值法将FLUENT温度结果不失真映射到ANSYS模型中，得到换热器温度分布，如图7所示，两种模拟方式获得的固体壁面温度分布几乎一致[9，10]。为了定量比较这两种方法，按图8所示方式编号，并将沿管长方向的温度数据绘制成图，发现两种方法预期的结果偏差都处于合理区间。

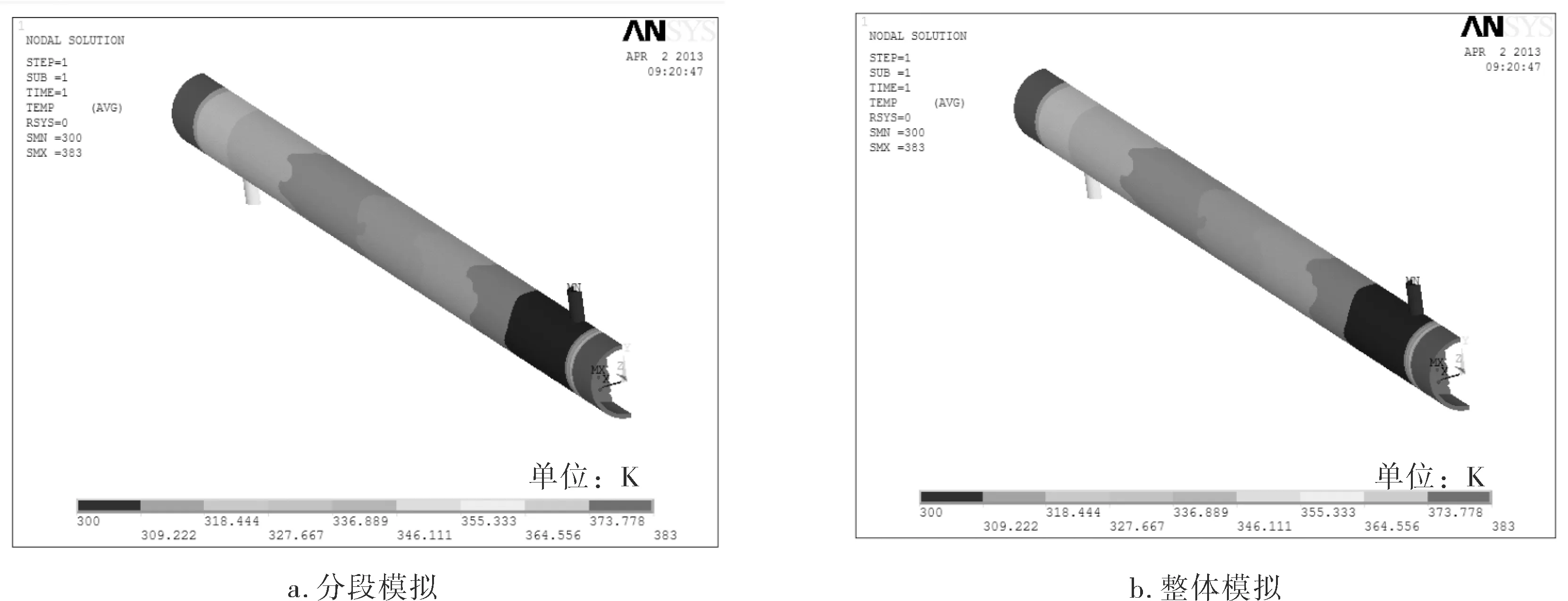
图7 ANSYS中不同模拟方式下的温度分布

图8 编号方式

4 模拟与实验对比

根据文献[8]的实验条件，将相同工艺条件下数值模拟结果与实验数据进行了对比分析。管板汽侧表面实验测点和路径定义如图9所示。模拟和实验数据的对比如图10所示。从图10可以看出，分段模拟和整体模拟结果在路径曲线上重合精度很高，与实验数据也比较吻合。

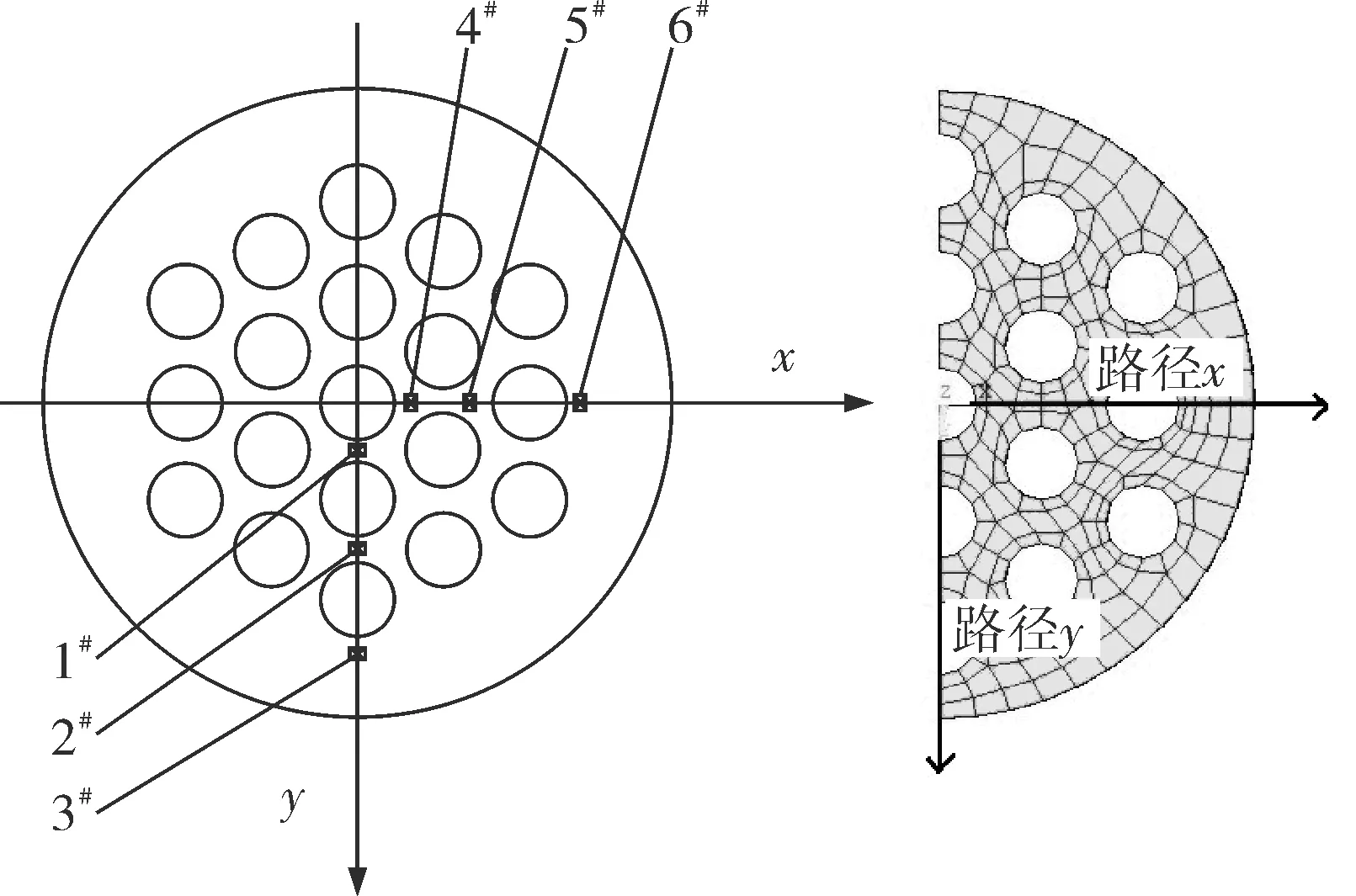
图9 管板测点和路径

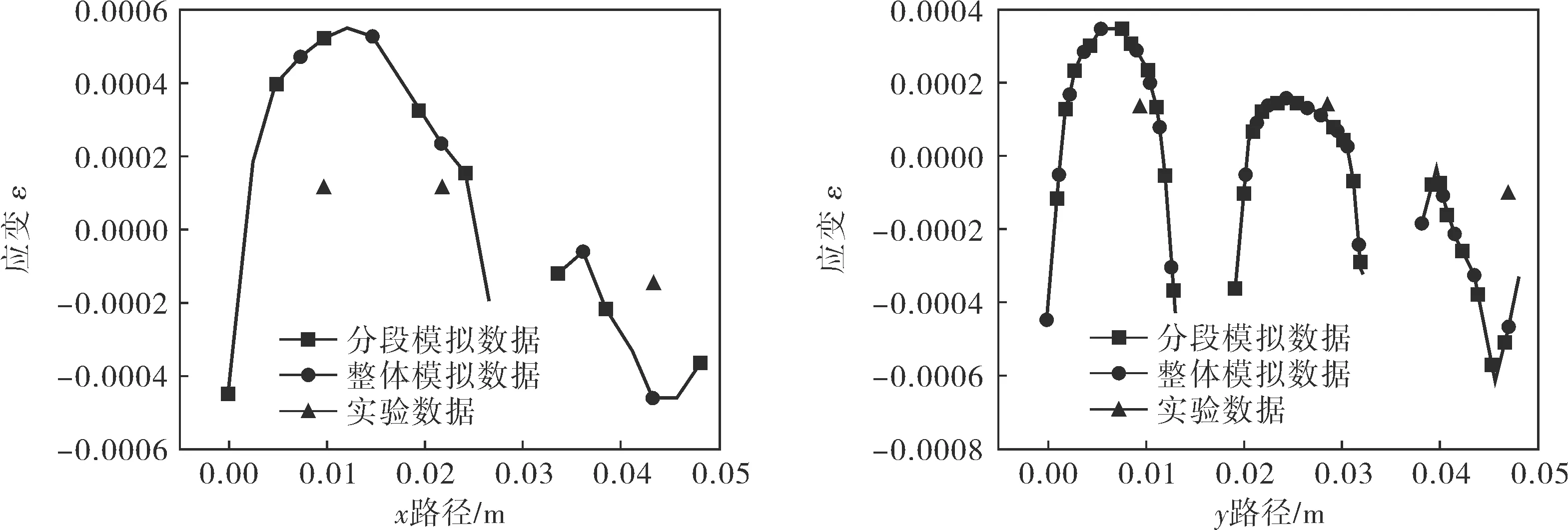
图10 路径x、y数据比较

5 两种模拟的差异

研究两种模拟方法差异的主要目的是考察各自对于求解实际工程模型的适应性。为便于说明，现保持换热器其他结构形式和尺寸不变，改变换热器长度和折流圈数目，利用相同的网格精度离散，并实施不同模拟方法的计算。表3给出了网格尺寸及类型。离散化网格数和平均网格精度见表4、5。

表3 换热器模型分块网格尺寸及类型

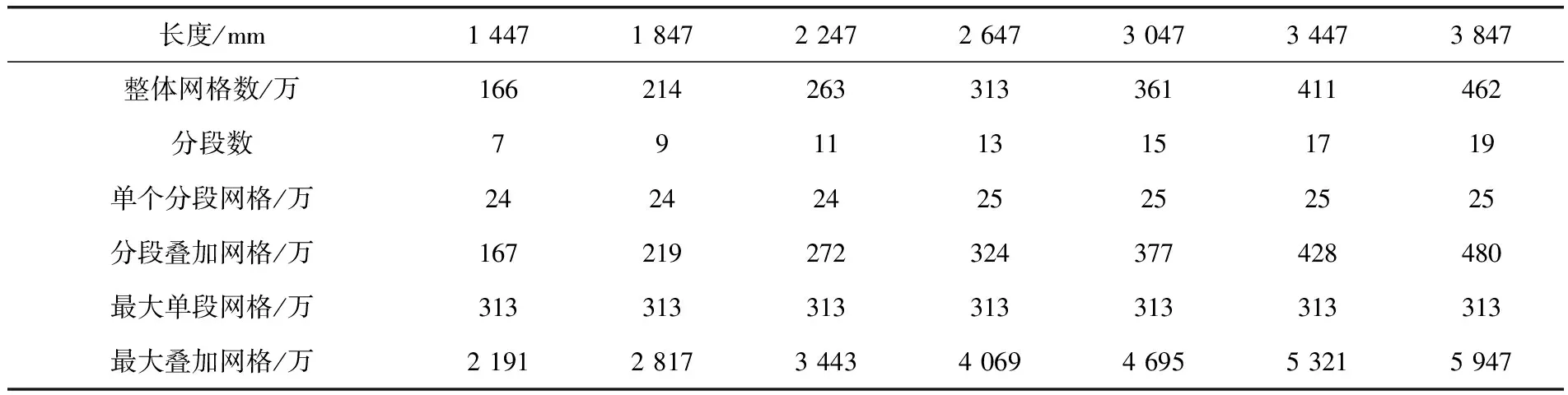
表4 各尺寸模型的网格数

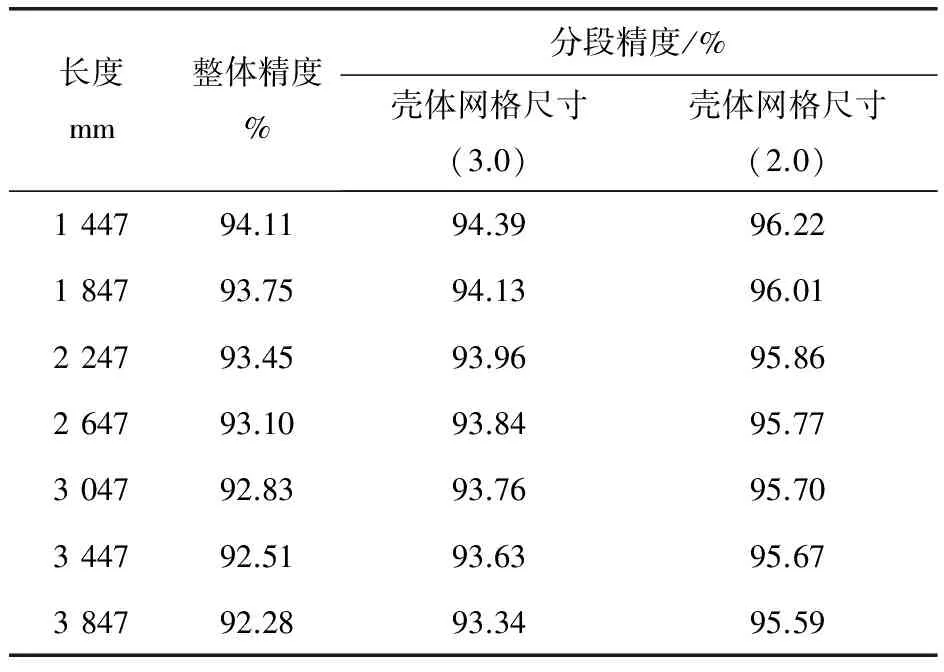
表5 各尺寸模型的平均网格精度

注：网格精度是网格扭曲率在0.6以下网格数占总网格数百分比。

由表4可以看出，分段数目随壳程长度的增加而增加，要达到与整体模型一致的计算效果，只需要创建单个段分网大致在24万～25万单元的模型就足够了。但是如果要提高计算精度，则整体模型已经达到极限，而分段模型的单个分段还可以继续提高离散化单元数目直到313万单元甚至更高，此时相当于把整体模型的几何尺度增加了十多倍，或者是把确定尺度的换热器计算精度提高十多倍。由此可见，如果只是保持原有的分网精度，分段技术可以处理更大的几何模型；也可以在保持模型尺度不改变的条件下，将离散化精度提高十多倍。换言之，相同的精度要求下，整体模型的计算单元如果是100万总数目，则分段计算的换热器单元总数可以达到整体模型的十多倍，网格精度大体一致。

表6的数据仅仅展示出离散化的情况，并不说明模型是否可计算。一般而言，单元总数目增加，计算速度逐渐降低，当模型尺度增加到一定程度(即网格增加到一定数量)时，计算机显示内存不足，无法完成计算。根据笔者所用电脑的实际情况，当分段的网格数目超过313万(即换热器长度为2 647mm)时，整体建模方法可以完成离散化，但是模拟计算已无法实施。这样看来，如果不放弃整体建模方法来实施模拟技术，则要完成大模型的模拟只能依靠提高电脑配置或者粗化网格(降低网格精度和计算成本)。但是通过改变模拟技术，采用分段建模，分段划网，分段模拟，整体综合的模拟方法，可以利用分块模拟的边界数据传递技术，一直计算下去。表6给出了这两种方法在实际模拟中的适应性对比。

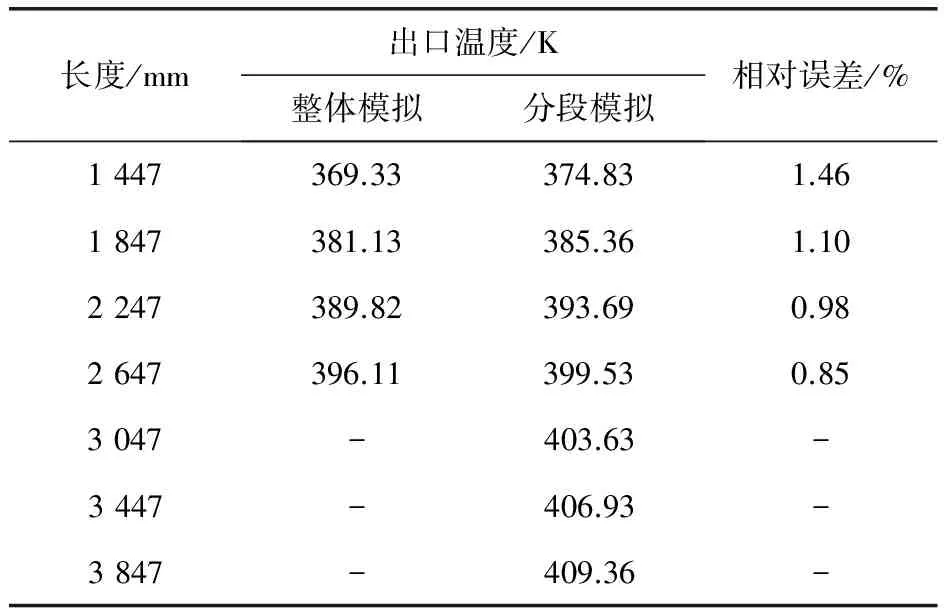
表6 各尺寸模型两种模拟方法的壳程流体出口温度对比

由表6可见，当换热器长度小于2 647mm时，整体建模跟分段建模方法结果一致，计算精度足够。但值得注意的是，当换热器长度继续增加时，对于整体法，即使已离散的模型，也无法通过计算，而在这种情况下，分段技术却可以继续实施。从计算实践看，分段模型可以继续进行，没有太大限制。但是整体模型早已无法实施计算。上述情况说明分段建模模拟技术无论是在计算规模还是计算精度方面都比传统整体模拟法更加优越。

如果在此基础上运用并行计算技术，那么分段模拟技术将具有更大的适用范围。随着并行计算平台的节点数增加，将有更多计算资源加入计算，所需时间减少,计算能力增强[12]。采用二、三、四节点并行时，完成相同计算任务，分别只需要原计算时间的52.7%、37.9%、29.6%，所以并行计算节约的时间相当可观。同时随着并行计算机器数量的增加，不仅计算效率提高，还扩展了可计算模型尺度。比如利用三节点并行，可将网格处理能力提高50%以上，而并行效率并没有大的下滑。利用文中配置进行三节点并行，以13个分段的模型为例，分段模型的最大叠加网格总数达到8 136万，而对应的整体模型网格总数只能达到616万，分段模拟的总网格数远大于整体模型。因此，分段模拟为解决大模型的模拟计算提供了一种可行的技术基础。

6 结论

6.1在计算规模较小的情况下，分段模拟可以更快获得具有足够精度的计算结果，该结果与实验结果较吻合，即此时分段模拟可以达到与整体模拟相同的计算要求。

6.2在计算规模比较大的情况下，分段模拟技术展示出很强的适应性，计算规模只受限于模型分段的大小，整体上基本不受限制，而此时整体计算模拟技术即使可以离散，也难以通过计算。

6.3在给定的几何尺度限制下，分段模拟技术可以将计算精度提高至少10倍；而在给定精度要求下，分段模拟的模型尺度可以扩展到10倍以上。

6.4利用并行计算技术，可以增强分段模拟技术的能力。

[1] 贺运初.换热器的强化传热与优化设计[J].化工装备技术，1997，18(2)：25～28.

[2] 曹纬.国外新型换热器介绍[J].化学工程，2000，28(6)：50～52，56.

[3] 王维慧.基于COMOSWORKS软件的固定管板式换热器应力分析方法[J].压力容器，2006，23(9)：21～24.

[4] 郭崇志，林长青.固定管板式换热器的温度场数值分析[J].化工机械，2008，35(6)：338～344.

[5] 郭崇志，周洁.固定管板式换热器的温差热应力数值分析[J].化工机械，2009，36(1)：41～46.

[6] 郭崇志，粱泉水.折流杆换热器数值模拟新方法[J].化工进展，2007，26(8)：1198～1206.

[7] 陈文昕.折流杆换热器的数值模拟与实验研究[D].广州：华南理工大学，2006.

[8] 粱泉水.预应力换热器的分析与实验研究[D].广州：华南理工大学，2007.

[9] 郭崇志，林长青.基于ANSYS和FLUENT的管壳式换热器整体分析方法[OL].http//pera.e-works.net.

[10] 郭崇志，肖乐.换热器流固传热边界数值模拟温度场的顺序耦合方法[J].化工进展，2010，29(9)：1615～1619.

[11] 林桥.预应力换热器传热与应力特性的数值模拟研究[D].广州：华南理工大学，2012.

[12] 郭崇志，肖乐.管壳式换热器数值模拟的并行计算技术研究[J].化工机械，2011，38(5)：604～606.