基于动态规划的机组启停优化研究
2014-05-29李元林李智张艳桃
李元林,李智,张艳桃
(国网浙江奉化市供电公司,浙江 奉化 315500)
1 引言
机组组合问题在很长时间内一直以调度周期内总运行成本最小为优化目标。但电力工业市场化改革后,目标函数相应演绎为购电成本最小,或更反映资源配置效率的社会总收益最大。环境污染问题的日益严重导致以排放最小为目标的尝试。当问题要顾及经济性、网络安全性以及排放许可等多个要求时,多目标模型就出现了。文献[1]用模糊逻辑方法解决有发电成本最小、网络安全、排放费用最小和可靠性成本最小四个目标的问题。文献[2]将各种多目标进化算法用于电力系统经济调度问题中,并进行了系统的对比与分析。在考虑燃料消耗量的同时,也研究了气体排放量的因素,将经济调度问题转换为带约束条件的两目标优化问题。文献[3]用动态规划法来优化机组退出过程,取得了与拉格朗日松弛法相当的优化效果和计算效率。用动态规划研究求解比线性规划和非线性规划更有效,特别是离散性问题,解析数学无用武之地,而动态规划成为得力工具。某些情况下,用动态规划处理不仅仅能做定性描述分析,而且可利用计算机给出求其数值解的方法。
2 建模分析
机组启停是要确定出一定研究周期内在系统中参于运行的机组的合理运行方案,使得在满足系统总负荷、运行安全和供电质量的前提下系统总耗量达到最小,它在电力系统的经济运行中扮演着重要的角色,好的机组启停方案可以节省大量的燃料费用。而机组启停最重要的一个环节是建立比较精确的数学模型。
2.1 机组耗量特性
电厂的成本可分为固定成本和可变成本,即发电总成本=总固定成本+总可变成本。采用燃料耗量成本来度量燃料耗量可以很好的反映机组发电所消耗的物化劳动,也将更为合理。用燃料成本作为输入F(单位为元/h)表示的F-P特性称为发电机组的成本特性。
单元机组的输入—输出曲线表达的是燃料输入率与发电机输出电能的函数关系,如图1所示。曲线上的起伏是由于汽轮机的几个调节汽门随着发出有功功率的增大而依次开放所形成的。即当上一级汽门开放时,蒸汽的流通会因节流效应产生损失,而导致耗量的增大,曲线向上凸起。
在分析计算时为了简便,通常用几个直线段或一条平滑曲线来近似代替上述有起伏的耗量特性,如图2所示。当用n段直线近似表示时,耗量特性可表示成:

式中,Pi-1≤P≤Pi,i=1,2…n;ai,bi为耗量特性参数。实践中更多的是采用平滑曲线来近似表示耗量特性曲线,通常采用的是二次曲线,可表示为:

式中,a、b、c为耗量特性参数。当然也可以用更高次数的多项式曲线来近似,但实践表明,次数增高并不能显著提高表达式的准确程度,而只会使问题的解析处理复杂化。所以,本文也采用二次曲线来表示机组的耗量特性,而机组的成本特性仅与耗量特性相差一个倍数而已。

图1 燃料能量输入率与输出功率的关系
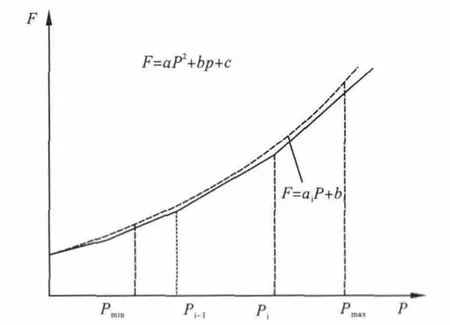
图2 火电机组特性的近似表示
耗量特性曲线确定之后,将某一时段的负荷分配情况代入耗量特性表达式,即可求得这一时段的机组运行成本。
2.2 机组启停成本
机组停机后再启动时要额外消耗一定的燃料,称为启动耗量。机组启动时,汽轮机系统要暖管、克服摩擦等,而锅炉要加温、加压,因此都要消耗一定的能量,也就是要一定的费用。其中,汽机的热容量很小,其启动耗量一般可近似当作一个与停机时间长短无关的常数。对于锅炉,由于其热容量很大,因而,从锅炉点火、产生蒸汽、升温升压、一直到锅炉各部分被加热到稳定状态的整个过程的燃料耗量与启动前锅炉的冷却程度有关而且数额较大。
机组的启动费用特性有两种模型,如图3所示。
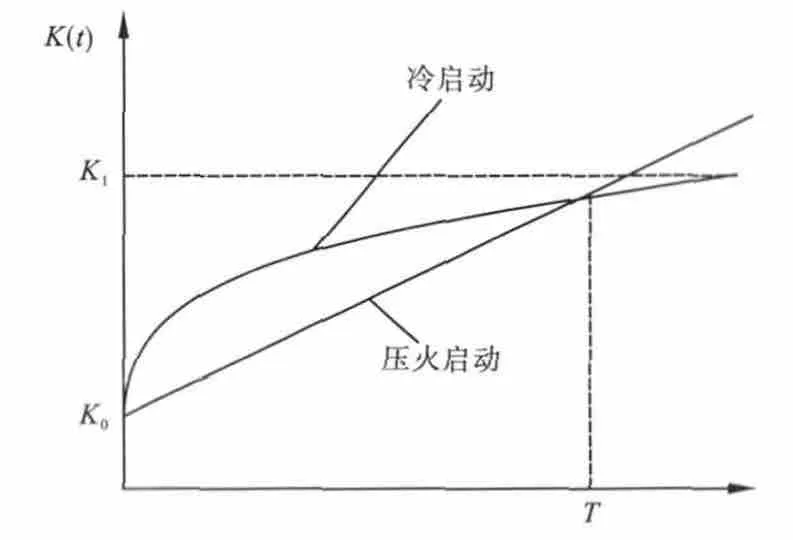
图3 启动费用特性
一种对应于机组由完全冷却状态启动,用指数函数表示,机组停炉停机后重新启动所需的启动费用k(t)和停机时间t的关系为:
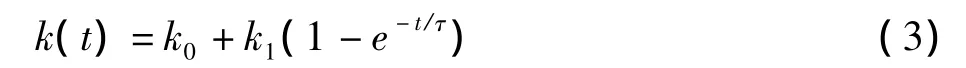
式中,τ为锅炉的冷却时间常数;k(t)为启动费用。k(t)分为两部分:第一部分k0是汽机的启动耗量,为固定费用(主要决定于汽机启动消耗的能量及运行人员的费用等);第二部分k1(1-e-t/τ)为锅炉由完全冷却状态启动时决定于热惯性的费用(主要决定于锅炉加温、加压)。
另外一种对应于机组压火启动(压火即保持锅炉、汽机一定的温度),也称热启动,用线性函数表示,机组压火t时间后再启动的启动耗量为:

k1为锅炉压火停运一小时所需的启动费用。
2.2 建立数学模型
(1)以时间划分阶段,设1个调度周期有T个时段,则划分成T个阶段,每个阶段对应系统1个具体负荷值;
(2)以各时段内可行机组组合为状态,设系统内有G个机组,每个状态矢量就有G维,每一维表示相应机组的开停机情况,1为开机,0为停机。
各时段状态矢量的个数是2G-1个机组组合中选出,满足以下约束条件的机组组合:

(3)时段间状态转移的决策:在计及最小停机和最小运行时间限制条件下,由前一时段的任意状态向后一时段的任一状态的转移必须满足最小停机和最小运行时间限制的要求。若满足,则决策变量为1,此转移有效;否则决策变量为0,此转移不能实现。
用 YJ[X(I,X-1)]表示(K-1)第时段第 I个状态向第K时段第J个状态转移的决策变量。
(4)以最小耗量函数(包括运行耗量和启动耗量)为最优指标函数,用f([J,K])表示由第1段诸状态到第K段第J个状态间各种转移中的累计耗量最低的路径的耗量。
(5)边界条件
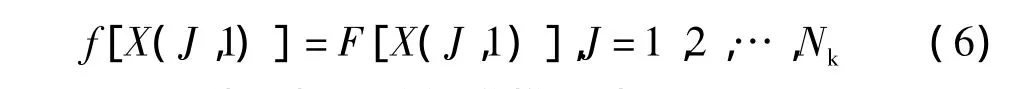
(6)最优目标函数的递推公式
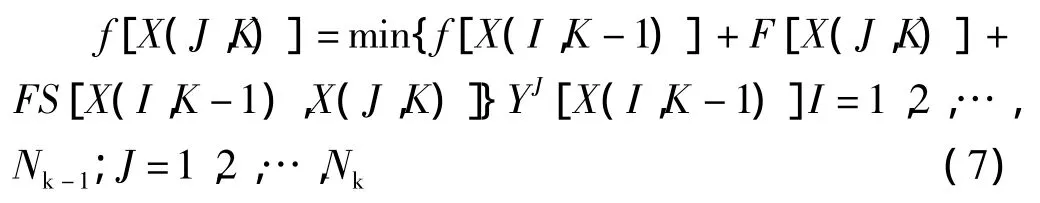
式中:F[K(J,K)]为第K时段上第J个状态的运行耗量;FS[X(I,K-1),X(J,X)]为从第(K-1)段的第1个状态到第K段的第J状态间各机组启动和停机费用之和。
3 算例分析
选用四种不同类型的发电机进行lingo仿真计算。每日电力需求如表1所示。

表1 每日用电需求(兆瓦)
每种发电机都有一个最大发电能力,当接入电网时,其输出功率不应低于某一最小输出功率。所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。这些数据均列于表2中。

表2 发电机数据
发电机使用的型号、数量以及发电机在每个时段工作时的输出功率不一致,很难精确地求出其最优解,因此,寻找出有效的近似求解算法就具有重要意义。
将每天分为7个时段,发电机使用总成本等于7个时段发电机使用成本之和。确定每个时段发电机使用的型号、数量以及发电机在每个时段工作时的输出功率,每个时段发电机使用成本分为启动成本、固定成本及边际成本,建立每个时段使用发电机所花费的成本的数学模型。工作的发电机组须留出20%的发电能力余量,正在工作的发电机组按照以80%的发电能力发电。第1时段发电机使用的启动成本与后6个时段发电机使用的启动成本算法有所不同,以分时段求出各时段的启动成本,求出的总费用为1915330元。得出模型最优解如表3所示。

表3 最优启停机组组合方式
4 结语
机组启停模型是建立在己经有了现货交易负荷预测结果。但是在电力市场的条件下这些都是不确定的,因此将来可以考虑在不确定的负荷预测和实时电价下来解决机组启停优化问题。文中优化火电机组启停问题仍属于单目标优化问题,可以将增大利润和减少成本结合起来考虑,建立一个多目标优化的模型来求解。
[1]Shahidehpour S M,Yamin Hatim,Li Zuyi.Market Operations in Electric Power System-Forecasting,Scheduling and Risk Management(M).John Wiley&Sons.New York,2002.
[2]M.A.Abido.Environmental/Economic Power Dispatch Using Multiobjective Evolutionary Algorithms[J].IEEE Transactions on Power Systems,2003,18(4):1529-1537.
[3]Li C,Johnson R B,Svoboda A J.A New Unit Commitment Method[J].IEEE Trans on PWRS,1997,12(1).
[4]Wang C,Shahidehpour S M.Ramp-rate limits in unit commitment and economic dispatch incorporating rotor fatigue effect[J].IEEE Transactions on Power Systems,1994,9(3):1539-1545.
[5]王民量,张伯明,夏清.考虑多种约束条件的机组组合新算法[J].电力系统自动化,2000,24(12):29-35.
