基于主成分分析法的火电厂选址综合决策
2014-05-28唐学文
唐学文
(广西电网公司南宁供电局,广西 南宁 530031)
1 引言
火电厂的选址是在满足一定可靠性约束的条件下寻求投资与运行费用最优的方案。这种单一追求成本最少的做法,必然是以其他目标被牺牲作为代价的。目前,许多研究都试图在发电厂规划[1-4]模型中尽可能去朵考虑一些相关影响因素,但是在优化规划阶段还是不容易将这些关联又矛盾的因素综合到同一个模型里进行求解。发电厂规划方案的综合决策可以弥补规划阶段的一些不足,对规划后确定的一些方案,从可靠性、经济性、适应性、环保性等多个方面进行定性或者定量的评价,最后建立数学模型对单个指标评价信息进行综合,得到最终确定的最优规划方案。
现行的火电厂综合评价应用中,常用的方法有模糊综合评价法、层次分析法以及两种方法的结合。文献[5]综合考虑了火电厂建设可行性的社会效益、经济效益、环境效益等多个因素,通过模糊综合评判法对火电厂的选址问题进行综合决策。文献[6]利用熵权法来处理火电厂选址评价中客观存在的不确定性与模糊性,熵反映数据本身的效用值求解各指标的权值,最后多层次模糊综合评价法得到方案优选结果。文献[7]综合灰决策方法与层次分析法,针对某些因素信息不完全的灰色性特点,进行火电厂规划选址决策。解决了传统建模方法和层次分析法难以解决的问题。文献[8]利用层次分析法结合定性和定量指标,首次对多目标多层次的火电厂选址问题进行了讨论。文献[9]建立了层次分析法和模糊综合评判法相结合的模型,解决了火电厂选址的综合决策问题。
目前解决火电厂规划方案综合决策问题的两种主流方法层次分析法和模糊综合评判法。这两种方法对各指标进行赋权都是由专家进行评判,比较容易受专家知识、经验、个人偏好的影响,主观随意性和不确定性较大。并且没有充分挖掘利用客观数据所提供的信息。
考虑上文所说的这些缺点,本文将主成分分析法(PCA)引入到火电厂选址方案的综合决策领域。采用主成分分析法仅利用客观数据便能得到方案的最后评价结果,评价结果相对客观。主成分分析法的基本原理与上述两种主流方法有较大的区别,它对解决火电厂选址优化决策系统开发和完善具有一定的参考价值。
2 火电厂选址方案综合评价指标体系
火电厂选址优选决策受到多种因素的影响,本文遵循科学性和独立性的原则,在已有的相关研究成果[10,11]基础上,从可靠性、经济性、适应性、环保性四个方面构建火电厂选址方案的综合评价指标体系。
3 主成分分析法
主成分分析法(principal component analysis,PCA)是多元统计学中进行数据简化降维的方法[12]。主成分分析法已经成功地应用于电力系统负荷预测、故障诊断、稳定评估等[13-15]领域中。PCA的基本原理是用少数几个不相关的数据,来替代原有较多的相关数据,并且使新数据成为原有数据的一个线性组合。即所选的新数据被称作主成分,选取主成分的原则是要尽量保留原数据中所含有的基本信息。利用统计学角度来分析,方差可以体现数据所含有的信息。方差越大,其数据所包含的信息量越大。

表1 综合评价指标体系
设由m个决策方案、n个指标构成的综合评价矩阵X=(xij)m×n,其中xij为方案i对于指标j的评价信息。利用公式(1)对指标信息进行标准化

式中:xj、Sj分别表示指标j的均值和标准差进行标准化处理后的指标数据 A=(aij)m×n=(A1,A2,…,An)满足:即标准化处理后的指标变量均值为0,方差为1。
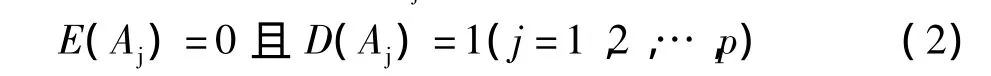
由标准化后的初始决策矩阵构建相关系数矩阵R= ( rij)p×p,系数矩阵的元素 rij表示指标 Ai和 Aj的关联程度。
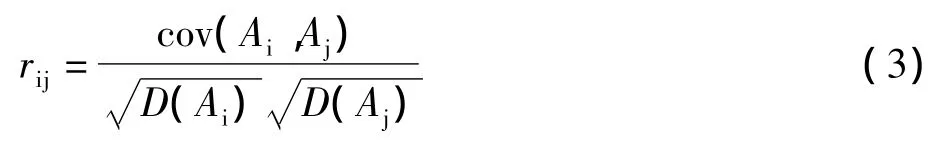
式中:cov(Ai,Aj)为指标Ai和Aj的协方差。根据公式(2)得到相关系数矩阵R与协方差矩阵相等。即相关系数矩阵为:

求出相关系数矩阵R的特征值,若R中有q个特征值大于零,特征值对应的特征向量为 P=(p1,p2,…,pq),即主成分为:

将上式表示成矩阵形式:

主成分求解的具体理论证明可参考文献[12]。它证明了主成分具有如下性质
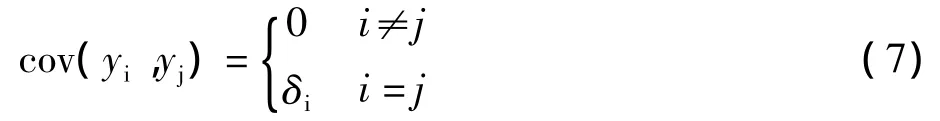
公式(7)表示主成分相互之间不关联,且第i个主成分yi的特征值δi为该主成分的方式。第yi个主成分的方差对总方差的贡献度:

贡献度wi表示第i个主成分所蕴含的原始信息的百分比。因此第一主成分的方差贡献度是最大的。这里定义前t个主成分的累积方差贡献度γ为

为了使评价体系中数据结构尽量简化,如果前t个主成分的累积方差贡献度γ达到一定目标时,则将t个主成分代替原有评价信息的n个指标。由t个主成分来形成综合评价函数:

定义主成分的方差贡献度为对应主成分的权重值。
3 基于主成分分析法的火电厂选址决策模型
建立主成分分析法的火电厂选址决策模型的过程:
(1)整理相关设计守则和规程,全面分析影响火电厂选址方案优劣性的相关因素,并遵循科学性、系统性和独立性的原则建立火电厂厂址候选方案综合评价指标体系;
(2)构建火电厂选址方案的初始决策矩阵V=(vij)n×m;
(3)对初始决策矩阵进行标准化处理,得到标准化后的决策矩阵为A=(aij)m×n;
(4)计算指标信息的相关系数矩阵R;
(5)根据计算相关系数矩阵R的特征根和特征向量来确定主成分;
(6)计算累积方差贡献度,选择m个起主要作用的主成分来表示指标信息;
(7)将m个主成分与方差贡献度形成综合评价函数,计算各方案的综合评价函数值并排序,得到最优决策方案。
4 算例分析
本文以国内某火电厂为例,先让相关设计部门进行规划设计初步确定三个候选厂址方案。通过各方案的实际数据进行统计得到经济性指标信息,采用专家评判法对剩下的指标进行打分并统计得到各指标的打分结果。各方案的评价矩阵如表2所示。

表2 各方案的评价矩阵
采用公式(1)对指标初始评价矩阵进行标准化处理。最终,得到标准化决策评价矩阵见表3。
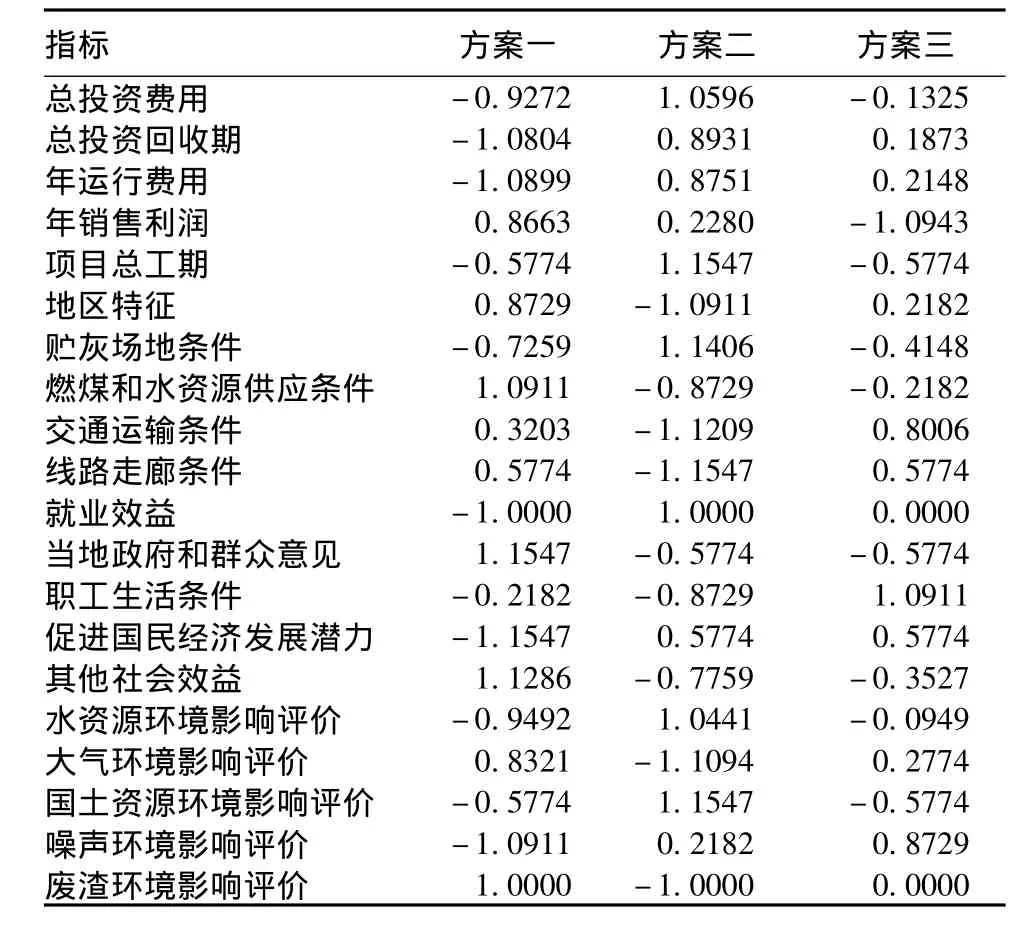
表3 标准化的评价矩阵
再按照前文所述方法,利用公式(3)、(4)对标准初始化矩阵进行运算,得到相关系数矩阵R。相关系数矩阵R主对角线上的元素都是1,矩阵中多数元素绝对值都是大于0.75的,表明了各评价指标之间的相关程度较大。
由矩阵分析的相关知识,求取矩阵R的特征根
及对应的特征向量,求解得出矩阵R的两个非零特征根,分别为 δ1=15.5047,δ2=4.4953,δ1与 δ2对应的特征向量分别为:

特征值δ1对应的方差贡献度为77.52%,因此只需要用一个主成分y1来代替原来指标数据信息,由l1来构造主成分y1与原指标的线性组合关系
y1= -0.2535A1-0.2481A2-0.2467A3+0.0684A4-0.2263A5+0.2516A6-0.2415A7+0.2465A8+0.192A9+0.2263A10-0.2536A11+0.213A12+0.0956A13-0.213A14+0.2374A15-0.2538A16+0.2494A17-0.2263A18-0.1560A19+0.2536A20
主成分y1对应的方差贡献度为77.52%,该主成分的权重为0.7752。最终的综合评价函数为:
3个待决策方案的综合评价函数值分别为2.9561、-3.1404、0.1844,显而易见最优火电厂选址方案为第一套方案。即候选厂址的优劣顺序为一、三、二。
模糊综合评判法[5]和灰色层次分析法[7]计算该实例结果见表4。明显地,两种方法所得的最优方案均为第一套方案,与本文模型所求结果一致。由于模糊综合评判法中,隶属度函数确定与最后的结果有很大的关系,而人为确定隶属度存在着很大的主观随意性。灰色层次分析法在权重确定过程中也存在一定的主观性。本文利用专家的经验和相关原始数据,构建了火电厂选址综合评价指标体系,引入主成分分析法来建立模型,有效地避免了综合评价过程中的人为主观性,排序结果之间的区分度较大,使结果更加客观、合理。

表4 其他方法评价结果
5 结论
本文对大型火电厂厂址选取的影响因素进行了分析和总结,将其细分为经济性指标、可靠性指标、适应性指标、环保性指标,在此基础上,引入主成分分析法,建立了基于主成分分析的火电厂选址综合决策的数学模型,通过实际算例进行验证,并将模糊综合评判法和灰色层次分析的结果与本文方法求得的结果进行了对比分析,验证了本文模型的客观性和有效性。本文所提方法思路清晰,计算简单,便于编程实现。而且不需要主观来确定权重,权重的确定完全依赖于客观数据特征,减少了评判过程中的主观因素和不确定因素,减少了电力决策者的工作量。
[1]杨勇平,刘殿海,杨昆,等.火电厂模糊优化选址[J].中国电机工程学报,2006,26(24):82 -87.
[2]吴耀武,侯云鹤,熊信艮,等.基于遗传算法的电力系统电源规划模型[J].电网技术,1999,23(3):10 -14.
[3]冯凯,李远德,侯云鹤,等.改进单亲遗传算法在电源规划中的应用[J].电网技术,2004,28(3):11 -15.
[4]贺峰,熊信艮,吴耀武.改进免疫算法在电力系统电源规划中的应用[J].电网技术,2004,28(11):38 -44.
[5]李艳梅,孙薇.多级模糊综合评判在火电厂选址中的应用[J].现代电力,2004,21(2):27 -30.
[6]梁冬青.基于熵权的模糊综合评价方法在火电厂选址的应用[J].煤,2010,19(1):3 -5,15.
[7]牛东晓.火电厂选址最优决策中的灰色层次分析法[J].电网技术,1994,18(6):27 -31.
[8]吕蓬,邢棉,康怡.火电厂选址最优规划中的层次分析法[J].华北电力学院学报,1994,21(4):99 -105.
[9]郭新志,乞建勋,李星梅.基于改进模糊层次分析法的火电厂选址综合评价方法研究[J].现代电力,2007,24(3):67 -71.
[10]牛东晓,李建青,马小勇.火电厂建设项目实施过程后评价指标体系研究[J].华东电力,2010,38(9):1416 -1420.
[11]段利东,牛东晓,吕海涛.火电厂建设项目影响评价及其环境因素分析[J].华东电力,2008,36(12):10 -12.
[12]余锦华,杨维权.多元统计分析与应用[M].广州:中山大学出版社,2005:193-197.
[13]刘宝英,杨仁刚.基于主成分分析的最小二乘支持向量机短期负荷预测模型[J].电力自动化设备,2008,28(11):13 -17.
[14]黄保海,李岩,王东风.基于KPCA和KFCM集成的汽轮机故障诊断[J].电力自动化设备,2010,30(7):84 -87.
[15]于之虹,郭志忠.改进主成分分析法用于暂态稳定评估的输入特征选择[J].电力自动化设备,2003,23(8):17 -21.
