双馈型风电机组的惯性控制

王琼，白丽燕，桑海燕，杨旭东，刘晓红

(兰州供电公司，甘肃 兰州 730050)

1 引言

风力发电作为目前技术比较成熟，经济效益较好的可再生能开发利用方式，已经被越来越多的国家列为能源发展的首要战略［1］。而双馈型风电机组以其具有较强风能捕获能力、改善风电场功率因数及电压稳定性的性能成为目前大型风电场的主流机型。双馈型风电机组通过转子侧接换流器实现对风电机组的变速恒频控制，捕获最大风能。中间的直流电压总线实现了电机与电网之间的解耦。因此，电网中频率的变化对发电机转子没有任何影响，因而其旋转动能被“隐藏”起来，对电力系统的惯量几乎没有贡献。随着系统中风机渗透率增加，电力系统表现出来的惯性将减少，因此各种系统突发事件(如发电机组的解列)或负载突然变化时会产生更高的频率变化率。这意味着旋转储备只剩较少的时间来调节功率失衡，这可能引起较大的频率偏差。

因此，有必要研究双馈风电机组的频率控制策略，进而提高含大型风电场系统的频率控制能力。本文从双馈型风力机组的惯性特性的角度出发，研究了频率的惯性响应阶段的控制策略。

2 双馈风电机组的模型及控制策略

DFIG在dq同步旋转坐标系下的磁链、电压、功率和电磁转矩方程为［2］:

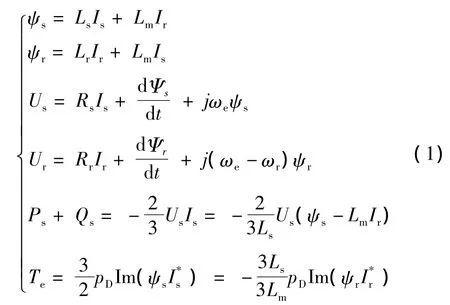
式中:ωe为同步角速度;ωr为转子电角速度;Us、Ur分别为定、转子电压矢量;Is、Ir分别为定、转子电流矢量;ψs、ψr分别为定、转子磁链矢量;Rs、Rr、Ls、Lr、Lm分别为定、转子电阻、等效自感和互感;Ps、Qs分别为DFIG的电磁转矩、定子侧有功、无功功率;pD为双馈电机的极对数。

忽略定子电阻及定子磁链变化，将同步坐标系的d轴定向在定子电压矢量上，由式(1)可得DFIG定子侧有功、无功功率和电磁转矩方程

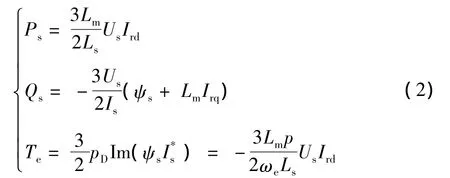
由式(2)可知，当采用定子电压矢量定向控制，并保持定子磁链恒定时，DFIG机组定子侧有功功率或电磁转矩可通过转子电流的d轴分量Ird控制，无功功率可以通过转子电流的q轴分量Irq控制，从而实现了有功和无功功率的解耦控制［3］。

双馈感应发电机的有功功率控制主要体现在最大风能捕获上。最大风能捕获指的是当风力机工作在切入风速和最大转速值之间时，通过调节发电机的转速，获取最大的风能利用系数Cp，进而使机组能够最大程度的吸收风能。

本文采用的最大风能捕获的基本原理如图4所示。发电机的有功功率经过转速－功率曲线得到转速参考值ωref，并与发电机实际转速ωr相比较，偏差值ωerr经过PI调节器得到参考转矩，再与发电机转速相乘，便得到发电机的参考有功功率Pord。将Pord与Vterm做除法运算得到发电机控制信号Ipmax。

图1 最大风能捕获原理图

在DFIG最大功率跟踪控制过程中，转子侧换流器仅根据风电机组转速变化调节有功输出。因此，当电网有功扰动时，风电机组仍然遵循其控制指令向电网输送功率，不能分担系统有功功率的变化，无法对系统扰动提供惯性支持。

风力机转子中存储的动能可以表示为:

式中，J为风力机转动惯量;ω为风力机转子转速。当系统频率从f0变化到f1时，转子转速将相应地从ω0变化到ω1，则风力机转子吸收或释放的旋转动能为:

由上式可知，若DFIG风电机组的转速运行范围为0.8～1.2(pu)，则通过改变风电机组的转子最大可以提供56%的转子动能。因此当DFIG风电机组或者风电场在电网中占到较大的比例时，其对整个系统转动惯量的贡献不容忽视。

可称式(4)为DFIG风电机组所具有的隐藏动能，当利用该部分动能使DFIG风电机组的"隐藏惯量"得到体现后，变速风电机组将具备类似同步发电机的惯性响应能力，并在参与系统调频过程中减小频率变化率的最大值。通过控制DFIG风电机组的转子转速变化，并利用其转子动能所得到的风电机组的电磁功率为［4］:

惯性时间常数往往表示发电机组利用其旋转动能提供功率输出所能持续的时间。若定义DFIG风电机组的惯性常数为H，则H可表示为:

式中，S为视在功率;ωs为风电机组的额定角速度。将H代入式(1.6)，且用标幺值来表示由转子动能所转换而来的电磁功率，可得到:

由上述惯性控制原理可知，在DFIG风电机组转子侧变换器控制系统中的有功功率参考值上增加一个与系统频率相关联的额外有功功率值，可对原来的功率控制环节进行修正，使得风电机组可在较短的反应时间内调整其有功输出，即对系统频率具有了有效的响应。当系统频率保持在其额定值且不发生变化时，该附加的频率控制环节将不起任何作用。而当频率发生变化时，频率控制环节开始根据控制需求来动作。系统频率下降时，DFIG风电机组通过附加频率控制环节来降低其转子转速，从而将部分转子动能转化为有功功率输入系统。反之，当系统频率升高时，DFIG风电机组通过提高转子转速来吸收部分电磁功率，并将转化所得的有功功率储存于风电机组的转子中，从而减少了有功功率的输出，即实现了此时风电机组参与系统调频的目的［4］。

综上可知，在DFIG风电机组的控制系统中增加一个额外的频率控制环节，既可以保持该种变速风电机组转速可控的优点，又能够使风电机组在系统频率变化时通过调节转子转速来吸收或者释放一部分转子动能，从而对系统频率产生有效的响应。

在运用DFIG风电机组的惯性控制法设计其附加频率控制环节时，通常是参考惯性响应实现的基本原理，通过系统频率的变化率来获得额外的有功参考信号，从而使DFIG风电机组具有虚拟的惯性响应［5］;

由式(7)可知，当系统频率变化时，利用系统中各同步电机的转动惯量所能获得的快速有功支持应当正比于发电机转子转速的变化率，也即系统频率的变化率。因此，运用虚拟惯性控制法所获得的额外有功参考信号ΔP可以通过一个与系统频率变化率的正比关系来得到［7－10］:

式中，Kf为控制比例系数，通常为定值。另外，在具体的控制设计中，往往还应加入低通滤波器等相关辅助控制设备，以消除控制信号中的噪声干扰或者个别过大的信号。

由第二章可知，得到的参考转矩，再与发电机转速相乘，便得到发电机的参考有功功率Pord，这样，附加的频率控制环节，既可以加在发电机的参考转矩上，进而影响发电机的参考有功功率(如图1)，也可以直接加在发电机的参考有功功率上，最终改变发电机的有功输出(如图2)［5］。本文选取的是第一种方法进行仿真。

图2 加在参考转矩上的惯性控制方法

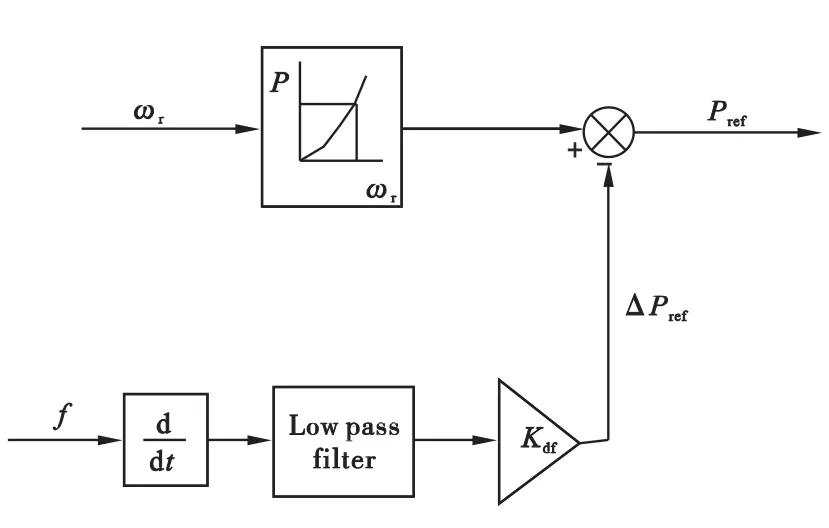
图3 加在参考功率上的惯性控制方法

频器中附加的频率控制模块不起任何作用。当系统出现功率缺额，频率发生变化时，双馈感应电机的有功功率参考设定点将会被附加的频率控制模块修改，参考设定点的值将等于电网频率变化率的函数。模拟的惯量正比于控制器常数，这个控制环节在电网频率超出指定的限值时会改变DFIG有功功率的设定点。

双馈感应风电机组在增加了附加频率控制环节之后，能够在电网频率发生变化时快速、有效的响应，改善了双馈感应风电机组的惯性特性。

3 仿真研究

3.1 基于Matlab/Simulink的仿真模型建立

为验证本文所提出的DFIG风电机组参与系统惯性控制策略的有效性，在Matlab/Simulink仿真平台上建立了一个含大规模风电并网的算例系统。该仿真系统是由一台同步发电机，一台风力发电机及负载若干组成，如图所示。

图4 仿真模型图

该仿真系统如图4所示，其中G1是一台额定功率为900MW的同步发电机，G2为一台等值了额定容量为600*1.5MW大规模风电场的DFIG风电机组，G3为无穷大电源，其作用只是启动DFIG风电机组，风电机组启动后，G3断开，L1、L2和L3都为系统负荷，其中L3是在DFIG风电机组稳定运行后投入的。每台同步发电机均配备了调速器和电力系统稳定器(PSS)，等值的DFIG风电机组则选取了simulink模型库中的DFIG average模型。

仿真中中搭建的惯性控制环节如图5所示。

图5 仿真时的惯性控制策略

3.2 仿真参数的设定

图5中，参数TS，K在仿真时并不是可以随意选取的，都有其对应的范围，当选去一个TS后，就有一个最大的K值。

选取 TS=0.1，0.2，0.5，1，2，5，10，仿真确定相应的K的最大值。

仿真结果如下:

图6 同参数时的加与不加惯性控制时的DFIG有功输出对比

图7 不同参数时的加与不加惯性控制时的DFIG有功输出对比

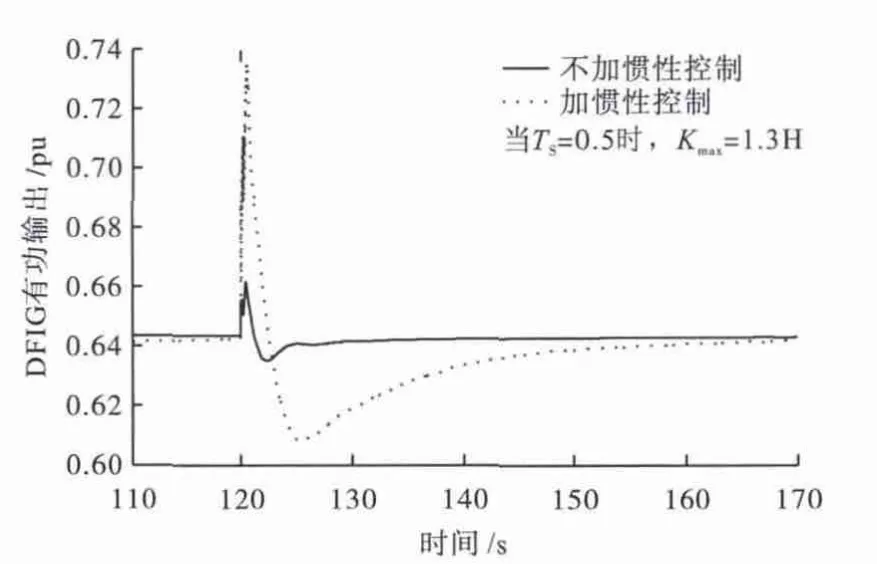
图8 不同参数时的加与不加惯性控制时的DFIG有功输出对比

图9 不同参数时的加与不加惯性控制时的DFIG有功输出对比

图10 不同参数时的加与不加惯性控制时的DFIG有功输出对比

从上述图可以看出，系数TS，决定了DFIG转子动能释放的快慢，TS越大，释放越慢;系数K决定转子动能释放的多少，系数K越大，转子动能释放的能量越多。

同时，当选取一个TS时，对应的Kmax/H有这样的关系:当TS较小时，Kmax/H是TS的2.5倍，当较大时，Kmax/H约是TS的2倍，并有倍数逐渐减小的趋势。

分析TS与Kmax的关系能够帮助我们在选取参数的时候更加有目的性，能够选取到更加合适的参数。

图11 不同参数时的加与不加惯性控制时的DFIG有功输出对比

图12 不同参数时的加与不加惯性控制时的DFIG有功输出对比

3.3 仿真结果

其中，参数TS，K的选取对于实验的结果有比较大的影响，选取TS=1，K=1.38H，仿真的结果如图13所示。

上图对比了无惯性控制和采用惯性控制的系统频率、DFIG功率及DFIG转速的动态响应。很明显，增加了惯性控制环节之后，系统频率下降的速率明显减小。当DFIG机组无惯性控制时，风电场对系统频率变化几乎没有响应;当DFIG机组采用惯性控制后，转子转速降低释放部分动能，转速下降幅度约为0.01pu，功率瞬时增加约为0.1pu，使系统频率降低的速度得到了有效减弱。

图13 频率变化时，加与不加惯性控制的DFIG的频率、有功、转速对比

从系统的频率曲线中可以看出，系统频率下降的速率虽然减小了，但是频率下降的幅值反而增加了。这是因为，DFIG增加了惯性控制后，当系统频率降低时，DFIG分担了一部分频率调节的功率，从而同步发电机的输出功率相对减少，从DFIG的有功输出与转子速度可以看出，DFIG转子速度降低，有功输出增加，但是，之后有一个DFIG转子速度恢复的过程，转速增加，输出功率减小，因而频率减小的幅值会增加。

4 总结

大规模风电并网后会给系统惯性响应带来不利影响，为提高风电并网后系统的稳定性，提高含风电系统的整体惯性响应能力，有必要对风电机组的惯性控制策略及方法进行深入的探讨和研究。因此，本文就目前多数风电场中所使用的双馈感应风电机组研究了其参与系统惯性控制的控制策略。 针对上述问题，本文开展了一系列相关研究，并得出了一些有益的结论，具体说明如下。

(1)普通同步发电机发电机在系统频率减小时，输出有功功率有所增加，对系统具有一定惯性响应;双馈变速风电机组在系统频率发生变化时，输出功率的变化量略有改变，对系统的惯性响应则十分有限。

(2)对双馈风电机组附加一个惯性控制环节，可以有效改善机组对系统的惯性响应特性，仿真分析表明增加了惯性控制环节的风电机组可以在系统频率波动的情况下，通过改变自身转子转速，吸收或者释放一部分动能，迅速平衡系统有功负荷波动，减慢系统频率波动。

［1］李俊峰，等.风光无限:中国风电发展报告2011［M］.2011，6.中国环境科学出版社，2011:1－46.

［2］贺益康，胡家兵，Lie Xu.并网双馈异步风力发电机运行控制［M］.北京:中国电力出版社，2012

［3］李和明，张祥宇，王毅，等.基于功率跟踪优化的双馈风力发电机组虚拟惯性控制技术［J］.中国电机工程学报，2012，32(7).

［4］曹张洁.双馈感应风电机组参与系统一次调频的控制策略研究［D］.西南交通大学.2009

［5］Xue Yingcheng，Tai Nengling，Review of contribution to frequency control through variable speed wind turbine［J］.Renewable Energy，2011，36(6):1671－1677.

［6］I.A.Gowaid，A.El－ Zawawi and M.El－ Gammal.Improved Inertia and Frequency Support from Grid－Connected DFIG Wind Farms.

［7］薛迎成，邰能灵，刘立群，等.双馈风力发电机参与系统频率调节新方法［J］.高电压技术，2009，35(11).

［8］R.G.De Almeida，J.A.P.Lopes，Primary Frequency Control Participation Provided by Double Fed Induction Wind Generators［C］.15th PSCC，Liege，2005:1 －7.

［9］Juan Manuel Mauricio，Alejandro Marano，Antonio Gomez－ Exposito，et al.Frequency Regulation Contribution through Variable － Speed Wind Energy Conversion Systems［J］.IEEE Transactions on Power Systems，2009，24(1):173－180.

［10］曹军，王虹富，邱家驹.变速恒频双馈风电机组频率控制策略［J］.电力系统自动化，2009，33(13):78 －82.