薄壁管材连续矫直截面扁化动态仿真分析①
2014-05-28张子骞杨会林
张子骞 杨会林
(东北大学机械工程与自动化学院 辽宁沈阳110004)
1 引言
近年来,高精度薄壁金属管材在工业、军事、医疗、航空航天、石油化工等领域中的需求急剧上升,为使管材具备较高的直线度和圆度,必须在出厂或使用前对其进行精整矫直[1-2]。薄壁管材一般采用多斜辊矫直设备通过多组轴向布置的等曲率矫直辊进行连续弯曲变形进而达到矫直的目的。每对矫直辊采用单一曲率半径设计,不同位置的矫直辊半径各不相同,由于管材初始曲率的大小和方向沿轴线各处不同,为此在入口处的初始矫直阶段,矫直辊弯曲半径设置接近极限弯曲半径,利用大塑性变形统一管材的弯曲程度,进而使管材在后续矫直中各截面具有相同的初始曲率。而管材特别是薄壁管材在大弯曲过程中其截面会随弯曲程度的增加不断扁化(即Bazier效应),故管材在经过初始弯曲后截面会发生畸变,必须在后续的矫直过程中通过径向挤压对截面进行矫圆。为准确设置矫直辊的压扁量,必须首先确定初始大弯曲过程中的最大扁化量以及弹复后的残留扁化量。
一直以来,许多学者对薄壁管材在弯曲过程中的截面扁化问题进行研究,有代表性的为YU等[3]给出的处理弯曲时截面扁化变形的普遍方法和原理,将Brazier处理圆柱壳弹性稳定性问题使用的能量方法[4]扩展到塑性领域,但针对薄壁管材的矫直问题尚需较多针对性工作。而现场仍然采用人工经验和反复试矫对弯曲扁化量进行估定,为此本文运用ANSYS/LS-DYNA对薄壁管材弯曲扁化的过程进行动态仿真,得到了最大扁化量和残留扁化量数据,并通过现场试验证明了分析结果的正确性,为现场矫直过程相关工艺参数的合理设置提供有效手段。
2 LS-DYNA薄壁管材弯曲扁化过程动态仿真
ANSYS/LS-DYNA是采用差分法进行积分计算的显式非线性动力分析软件,其算法特别适合于分析各类高度非线性的复杂力学过程。如爆炸和冲击、结构碰撞、金属加工成型等问题。薄壁管材连续矫直截面弯曲扁化变形过程属于大弹塑性变形,LS-DYNA对这类问题的处理效果较好。
2.1 模型简化与仿真条件
文献[5]对薄壁管材在等曲率矫直辊中的矫直工作过程进行了仿真模拟,在该结构模型中管材在辊缝中螺旋前进,在某一时刻管材截面在某一方位上发生弯曲扁化,随着管材的旋转该方位上随即发生卸载弹复,此时管材该截面在另一方位上又发生弯曲扁化,因此弯曲扁化和弹复过程必然相互影响,同时弯曲过程中和弯曲结束后截面扁化的方位难于准确确定,使得弯曲扁化量和残留扁化量都很难测准。为此基于文献[5]的纯弯曲假设,忽略辊形、辊距、倾角、压下量等因素的影响,建立了如图1所示的有限元模型,由上弯曲模、薄壁管材和下部两个支撑辊组成,上弯曲模的半径接近管材的临界弯曲半径,且上弯曲模有一定长度,保证薄壁管材在小弯曲半径下发生纯弯曲变形,弯曲模与管材的接触状态与实际矫直辊与管材接触状态相似,这样该模型可用于对薄壁管材矫直过程截面扁化的动态仿真研究。
仿真过程的建模参数如下:矫直材料为不锈钢1Cr18Ni9Ti,屈服极限 σs=205MPa,弹性模量E=206GPa,切线模量 E1=2GPa,管材外径 d=21mm,壁厚t=1mm,管材长度500mm,管材初始弯曲半径约为8m。上弯曲模的半径Rw=4.26m,下支撑辊距离为350mm。
2.2 材料属性
上弯曲模和支撑辊在矫直过程中仅发生较小的弹性变形,故在仿真过程中可视为刚体,其材料为Rigid Material。薄壁管材在矫直过程中发生大弹塑性变形,可将管材定义为经典双线性随动强化材料,即应力、应变关系采用两条不同斜率的直线简化。相关材料属性定义如下:DENS(密度)为7850kg/m3,EX(弹性模量)为 203GPa,NUXY(泊松比)为 0.3,Yield Stress(屈服极限)为 205MPa,Tangent Modulus(切线模量)为 2.03GPa,是弹性模量的1/100。
2.3 三维有限元模型
根据上述参数在Solidworks软件中建立上弯曲模和支撑辊三维模型,并与薄壁管材装配后导入ANSYS/LS-DYNA中,上弯曲模和支撑辊由于是实体结构,采用用SOLID164六面体实体单元进行网格划分,而管材由于壁厚很薄可以忽略厚度,故选择SHELL163壳单元进行网格划分,由于管材是变形过程中的主要受力对象,为此网格采用扫掠法划分较密,经网格划分后的模型如图1所示,共生成14564个节点。

图1 有限元仿真模型
2.4 接触与摩擦
为对图1所示模型进行正确的仿真分析,必须正确定义接触。而模型在定义接触前需要首先创建组元,这里创建的组元分别为上弯曲模(WQM)、支撑辊(ZCG)、管材(GC)共 3个。在LS-DYNA中接触的类型主要有三类:单面接触、节点与表面接触、表面与表面接触,压弯过程符合表面与表面接触类型,定义上弯曲模和支撑辊的组元WQM、ZCG分别与管材组元GC为表面与表面接触,接触类型设定为自动接触。同时管材在上弯曲模的作用下压入支撑辊的过程通常包括滑动摩擦和滚动摩擦,这里设置滑动摩擦系数为μs=0.15,滚动摩擦系数为 μd=0.01。
2.5 施加边界条件
薄壁管材弯曲扁化的过程仿真涉及两类边界条件,一类是运动约束,这里支撑辊的自由度在单元属性中被完全限制,上弯曲模在单元属性中被限制了除沿y轴平移外的其余五个自由度,管材的自由度不做限制可自由变形;另一类是载荷,压弯过程需要通过上弯曲模的移动对管材施加压力,这里需要对上弯曲模施加位移载荷,该载荷采用位移—时间曲线的控制方式来加载,运用数据表输入不同时间点对应的上弯曲模y向位移。
2.6 仿真结果与分析
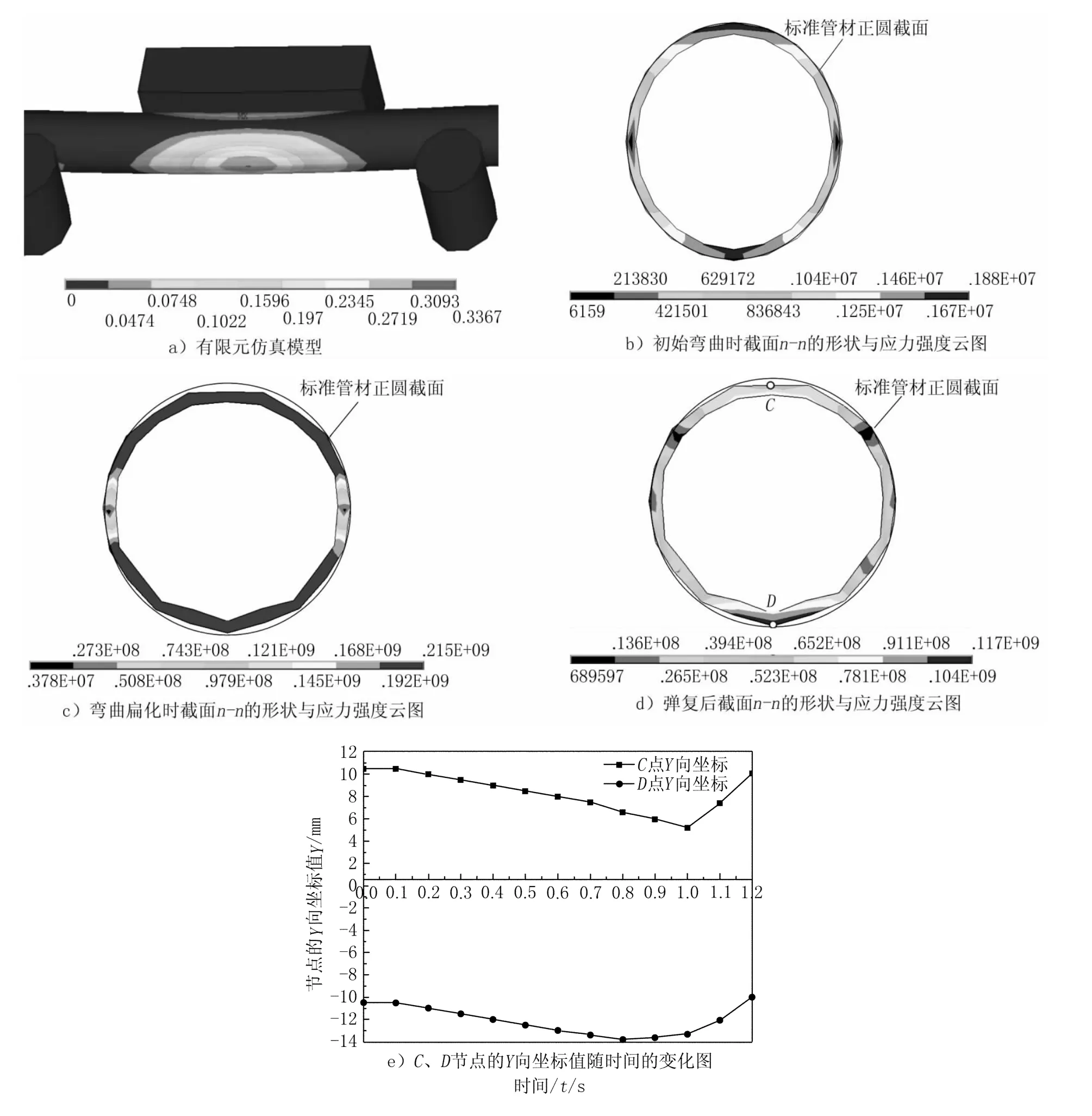
图2 薄壁管材弯曲扁化过程动态仿真结果
仿真过程中管材在上弯曲模的带动下被压入到下部两个支撑辊中,当上弯曲模与薄壁管材完全重合时,管材轴线的弯曲半径即为上弯曲模的半径,此时管材在小弯曲半径下发生弹塑性变形,管材的应变强度云图如图2a)所示,这里取管材长度方向上中点处的横截面n-n,图2b)为初始弯曲时截面n-n的形状与应力强度云图,可见此时应力水平较低,截面仍为圆形。图2c)为管材与上模完全接触时截面n-n的形状与应力强度云图,此时应力水平较高,截面与正圆相比发生了扁化。图2d)为管材与上模完全分离后截面n-n的形状与应力强度云图,此时截面存在残余应力,截面与正圆相比仍存在残留扁化变形。为准确确定弯曲扁化变形过程中的截面的最大扁化量和残留扁化量,分析管材截面变形程度最大的2个节点CD(如图2d)所示)的纵向(Y向)坐标随时间的变化情况,如图2e)所示,由图中可见,当t=1s时CD两点径向距离约为18.6mm,故最大弯曲扁化量约为2.4mm,当t=1.2s时CD两点径向距离约为20.1mm,故残留弯曲扁化量约为0.9mm。
3 现场试验验证
为验证仿真结果的正确性需进行现场试验,采用YC10GJ—70薄壁管材矫直机,如图3所示,采用二梁6柱的12斜辊式结构,矫直辊成对布置,第1、3、4、6 对辊采用准双曲线辊形,第 2、5 对辊采用深、浅凹形等曲率矫直辊,管材在第2对辊内通过大弯曲变形使初始曲率统一,故此处变形程度大采用大辊径设计。试验选用10根初始弯曲程度差别不大的不锈钢1Cr18Ni9Ti薄壁管材,管材参数如2.1节所述,依次送入矫直机进行矫直,在管材通过第3对辊后停机,此时对管材在第2对辊缝中的最大截面扁化量进行粗测,近似结果列于表1中,而后抬起上辊取出管材,对弹复后的管材截面沿着不同方位进行粗测,得到管材的最大残留变形量列于表1中。这里去掉表中同类数据的最大和最小值,而后将平均值作为试验值,得到截面的最大扁化量为2.27mm,最大残留扁化量为0.88mm,通过与仿真结果对比发现仿真值比试验值稍大,但偏差量不大控制在10%以内,而最大扁化量结果相差较大,这是由于在实际试验中,管材被矫直辊压紧,测量管径只能靠卡尺卡在矫直辊与管材间的缝隙测量,所测位置并不能保证为截面扁化量最大的位置,故实测值偏小。这样便通过现场试验证明了动态仿真结果的正确性,以及仿真模型简化的合理性。

图3 薄壁管材弯曲扁化过程的现场试验
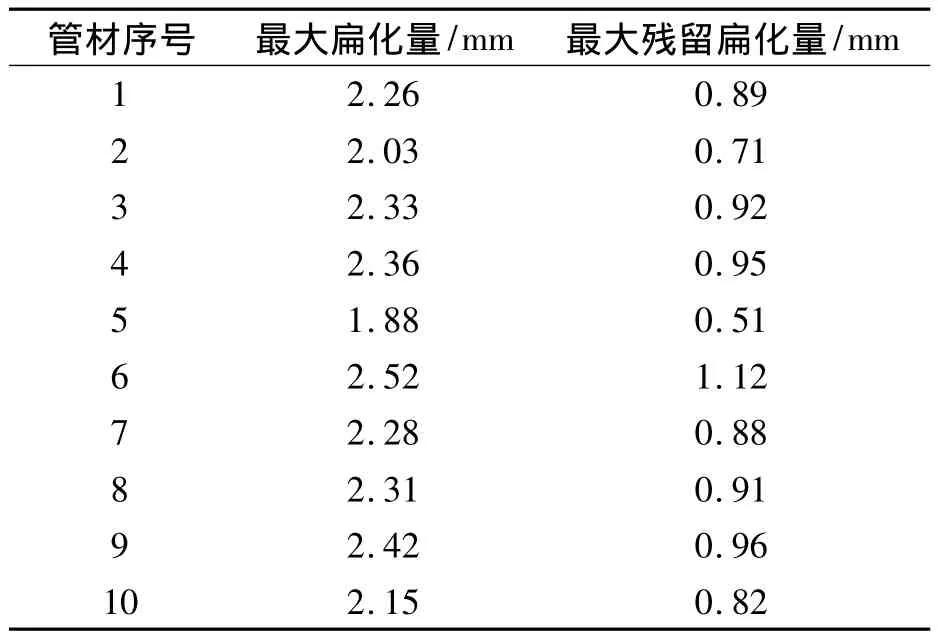
表1 最大扁化量和残留扁化量的现场试验值
4 结论
针对薄壁管材矫直过程截面畸变问题,采用ANSYS/LS-DYNA对薄壁管材弯曲扁化过程的动态仿真可确定管材截面的最大扁化量和残留扁化量;通过与生产实践数据的比对证明仿真结果是正确和可信的,为薄壁管材矫直工艺参数的确定提供了理论依据;采用仿真分析的思路和方法可推广移植到其他形状截面管材弯曲扁化工艺量的确定中去。
[1]张子骞,杨会林,田永利.薄壁管材矫直过程应变中性层偏移模型与分析[J].中国机械工程,2013,Vol.24(10):1390-1395.
[2]张子骞,颜云辉,杨会林.薄壁管材矫直曲率半径数学模型及其验证[J].机械工程学报,2013,Vol.49(11):160-168.
[3]Yu Tongxi,Zhang Liangchi,Plastic bending:theory and application[M].World Scientific Publishing Co Pte Ltd,1996.
[4]L.G.Brazier.On the flexure of thin cylindrical shells and other thin sections[J].Proceedings of the Royal Society of London.Series A,Containing Papers of a Mathematical and Physical Character,1927,Vol.116(773):104 -114.
[5]张子骞,张柏森,杨会林,等.管棒材等曲率矫直力模型可视化设计[J].东北大学学报(自然科学版),2012,Vol.33(3):409 -413.
