基于改进随机蕨的移动机器人物体识别算法
2014-05-27曾春年
梁 红,张 哲,徐 帆,曾春年
(1.武汉理工大学 自动化学院,湖北 武汉430070;2.武汉理工大学 信息工程学院,湖北 武汉430070)
随着计算机技术、自动化技术和传感器技术的发展,智能机器人成为当今的研究热点,对于智能移动机器人的研发来说,视觉是其中的一个重点,其物体识别备受关注。一方面,物体识别的能力代表了机器人认知能力;另一方面,物体识别的研究成果可以用于即时定位与地图构建、智能监控、人机交互系统和机器人环境感知等领域。很多成熟的移动机器人平台已经实现了特定物体的识别,从而使机器人拥有更为丰富的技能,如Willow Garage 公司的PR -II 机器人,可对各种杯子进行识别和姿态预测[1],并能根据指令为人们提供各种饮料;Aldebaran 公司的Nao 机器人,用摄像头捕捉目标物体图像后,通过WiFi 传到主服务器上,在主服务器上进行学习和识别,并可把自己的学习经验分享给其他Nao 机器人[2];Sony 公司的Aibo 机器狗,可完成机器人足球比赛。
虽然在计算机视觉领域,物体识别已经是多年的研究热点,也有相当多可供研究的数据库,但这些成果并不能直接被移动机器人所使用。相较于传统物体识别的各个难点,如光照影响、旋转影响、视角变化、遮挡等,移动机器人还面临着因移动带来的运动模糊以及复杂背景。同时它对算法的实时性要求也相当高,而很多算法之所以取得好的性能,往往是通过牺牲实时性做到的。
因此针对移动机器人物体识别的应用,需要寻找一个实时性较好,同时又要保证性能的算法。物体识别常用的一种方法是关键点匹配,其算法思路是提取目标物体图像的关键点和待识别图像的关键点,然后进行关键点匹配。根据关键点的匹配情况判断待识别图像中是否包含目标物体。根据关键点的不同描述和匹配方法,分为两个大类:一类是构造特征不变描述子,一般来说,高维描述子独特性更好,但耗时;低维计算量小,但损失关键点特性。常用高维进行描述,再用各种方法降维。MIKOLAJCZYK 等对10 种局部描述子做了不变性实验,结果表明,尺度不变特征(scale-invariant feature tansform,SIFT)算子及其扩展算法在同类描述子中具有最强的鲁棒性[3];另一类是对关键点进行统计特性分析,这种方法需要采集足够的目标物体图像样本,在很多应用中,限于技术条件无法做到。变通的方法是根据一个目标样本,经过模糊、扭转、缩放等变换,构造出目标物体图像各关键点的样本集。此类算法的代表有随机树[4]和随机蕨[5]。前者对关键点处图像小块(patch)用一种层次结构描述。后者对关键点处图像小块用无层次结构的二进制特征来表征。
从性能和速度的比较来看,基于二进制特征的随机蕨算法可达到接近标准SIFT 的识别率,所需时间大大减少,因此随机蕨算法更适合应用在移动机器人上。然而该算法也有一定的局限性,由于其关键点的描述并没有明确物理意义,其独特性不够强,误匹配率较高。另外,移动机器人采集的图像有一定的特点,如分辨率一般不高。这是由于带宽和性能的限制,高分辨率的视频摄像头无法应用到移动机器人上,通常在移动机器人上配备的摄像头分辨率为640×480。移动机器人所处的环境光照比较复杂,这就造成采集的图像曝光不一定很准确。过曝和欠曝的情况时有发生,过曝会造成信息量减小,欠曝又会造成噪点干扰和运动模糊现象。移动机器人所处的环境在不断变化,其背景物件也随之变化,没有固定的特征,显得杂乱无章。所有这些因素对物体识别算法提出了更多和更高的要求。因此需要在常规随机蕨算法的基础上进行改进和优化,根据移动机器人待识别图像的特点,通过对参数的调整以及匹配标准的改进,获得更高的识别率,同时保持较低的识别时间。
1 随机蕨算法思想和参数选择
1.1 目标图像关键点提取和统计样本构建
随机蕨算法的关键点检测子是LE PETIT 提出的,是基于harris 角点检测的,可设定参数,检测最稳定的Hobj个关键点。以保证这Hobj个关键点最能体现目标体的特征。
对关键点的图像小块进行二进制描述,设图像小块的尺寸为L×L,则二进制码中每一位的值取决于在该图像小块中随机取两点比较灰度值后的结果:
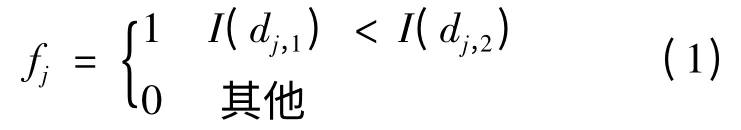
这种表述方式很简单,为了保证其独特性,必须保证二进制码的长度N,一般N至少需要300位以上。将各关键点所属类用Ci(i=1,2,…,H)表示,根据贝叶斯公式:

如将fj分为M组,每组包含S=N/M位二进制码,并假设不同组的二进制码相互独立,同组内二进制码具有相关性,则式(2)可近似为:

这些组就称为随机蕨(ferns),关于相关性的假设虽然在事实上不一定成立,但OZUYSAL 所作实验表明,无论是随机的分组还是按一定的相关性分组,对结果的差异都不大。但显然随机分组在计算上更容易实现。
1.2 构建统计样本模型
为了使根据统计样本获得的分类器具有鲁棒性,通过如下变换矩阵来构建样本:

其中,Rφ和Rθ分别为角度为φ 和θ 的旋转矩阵,φ 和θ 为生成样本的旋转角度,φ,θ∈[-π,π];diag(λ1,λ2)为缩放矩阵,λ1,λ2为生成样本的缩放范围,如果目标图像与待识别图像之间尺度变化不大,则λ1,λ2范围可选择较小值;如果尺度变化大,则λ1,λ2范围需选择较大值。同时在此基础上,添加了范围[0,255],方差25 的高斯白噪声。从而使分类器对旋转、扭转、缩放和噪声都具有一定的鲁棒性。得到这些样本后,通过同样的方式进行二进制码描述,每个关键点取10 800 个样本。根据这些样本,可以获得蕨类的统计特性。
1.3 待识别图像中关键点的提取和匹配
待识别图像中关键点的提取与目标图形关键点的提取方法基本一致,也可以确定Himg个最稳定的关键点,因为待识别图像一般都具有干扰物,所以参数选择时,必须确保Himg>Hobj,这样才可以保证待识别图像中有足够关键点与目标图像中的关键点进行匹配。得到关键点后,对图像小块进行描述,小块尺寸仍为L×L。通过式(3)可以计算出这串二进制描述从属于哪一类,即与目标图像的哪个关键点匹配的概率最大。
2 数据库和评估函数的选择
用于物体识别的数据库非常多,如加利福利亚理工学院的Caltech101[6]数据集,Pacal VOC 竞赛的数据集[7],都是业内认可的性能比较数据集。但是,作为移动机器人的待识别图像,其实际呈现出的效果与这种人工痕迹比较重的图像有所不同,其分辨率一般较差,运动模糊的现象也比较严重。因此,笔者选用的数据库是RAMISA 等制作的移动机器人数据库IIIA30[8]。它的待识别图像全部是从真实的移动机器人采集的实时视频得到的,一共有30 个类别(29 个物体和背景),2 450 个图像,其部分图像如图1 所示。
笔者采用的评估函数为正确率Pre和召回率Rec,其定义为:
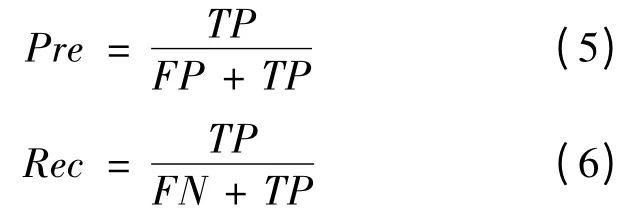

图1 IIIA30 中的待识别图像
其中:TP为有该物体,判断也是有该物体;FP为没有该物体,判断有该物体;FN为有该物体,被判断没有该物体。
因此Pre即是所有判断有该物体的图像,确实有该物体的比率,也就是正确率。Rec是所有确实有该物体的图像被判断出来的比率,也就是召回率。
3 实验结果和分析
在实验中,测试了几组关键点数目的数据,Hobj为目标图像中关键点的数目,Hobj取100,待识别图像因干扰较多,关键点的数目Himg取500,小寸L为32,设置M=40 个随机蕨,随机蕨的位数S=11。
分类器建模中旋转矩阵参数φ,θ∈[- π,π],缩放矩阵根据待识别图像与目标图像之间大小关系,设为λ1,λ2∈[0.6,1.5],共生成10 800幅图像,
对于基于关键点方法的物体识别,一般以关键点匹配数目作为标准来判定待识别图像中是否有该物体,如文献[9]。笔者最初也是用这种方式来进行判断,但发现效果并不太好。对识别效果特别差的图像进行分析,发现由于移动机器人所取的图像分辨率低,得到的关键点相当少,匹配数目也相应减少。因此这种仅用匹配数目的绝对数量进行判别的方式显然不适用于移动机器人的物体识别。在2 450 个数据图像中,按所设定的参数,关键点数目取500 个,仍有500 个图像中实际找到的关键点小于10。因此仅按传统的关键点匹配数目作为标准是不合适的,于是引入另一个参量,即匹配分数,其定义为:

其中:hnum为关键点匹配数目;hobj为实际找到的目标图像关键点数目;himg为实际找到的待识别图像关键点数目。H为设定的寻找关键点数,h为实际取得的关键点数目,显然h≤H,则hobj≤Hobj,himg≤Himg。
匹配分数的引入使那些关键点很少,但都是正确匹配的待识别图像,可以得到正确的判断。最后判断待识别图像是否有该物体的函数成为一个两参量的函数,即F(hnum,S)。该函数的结果值为布尔量,在S值一定的情况下,hnum取值越大,则Pre越大,Rec越小。这也是符合理论依据的。因为hnum越大意味着判断有特定物体的标准更为苛刻,这自然带来更高的正确率和更低的召回率。在hnum值一定的情况下,S取值越大,同样是Pre越大,Rec越小。需要注意的是,如果S值和hnum取其范围的最大值,Pre反而会下降,因为过于苛刻的判断标准可能导致TP为0,则Pre也为0。根据hnum和S取值范围,测试各组数据,求取使Rec不过于低(均值大于0.2),Pre尽可能高的取值。最后采用的数值为hnum大于9,S大于0.5。
运行算法所用计算机配置为:i5 -4430 @3.00 GHz 四核,4 G 内存,WIN7 64 位系统,得到的结果如表1 所示。

表1 不同类别的正确率和召回率
原始随机蕨算法的平均正确率为0.49,改进随机蕨算法为0.82,提高了0.33。原始随机蕨算法的平均召回率为0.44,改进随机蕨算法为0.22,仅有小幅下降。其平均运算时间为22.56 ms。
4 结论
笔者介绍了一种针对移动机器人摄取图像进行物体识别的随机蕨算法,该算法是基于关键点匹配的。根据移动机器人采集图像的特点对随机蕨算法进行了改进和优化,在目标图像中提取足够的关键点,并进行描述和统计学分析,当待识别图像中被匹配的关键点数目达到所设定的标准时,认为待识别图像中包含该物体。从实验结果可看出,改进随机蕨算法保持了较低的运算量,实时性好,同时优化算法达到了较高的识别正确率。
[1]RUSU R B,BRADSKI G,THIBAUX R,et al. Fast 3D recognition and pose using the viewpoint feature histogram[C]∥Intelligent Robots and Systems(IROS),2010 IEEE/RSJ International Conference.Taipei:[s.n.],2010:2155 -2162.
[2]SMOLAR P,TUHARSKY J,FEDOR Z,et al. Development of cognitive capabilities for robot Nao in center for intelligent technologies in kosice[C]∥Cognitive Infocommunications (CogInfoCom),2011 2nd International Conference . Budapest:[s.n.],2011:1 -5.
[3]MIKOLAJCZYK K,SCHMID C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(10):1615 -1630.
[4]LEPETIT V,FUA P. Keypoint recognition using randomized trees[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(9):1465-1479.
[5]OZUYSAL M,CALONDER M,LEPETIT V,et al.Fast keypoint recognition using random ferns[J].IEEE Transactions on Pattern Analysis and Machine Intelligence ,2010,32(2):448 -461.
[6]FEI - FEI L,FERGUS R,PERONA P. The caltech 101 dataset[DB/OL].[2014 - 02 - 15]. http://www. vision. caltech. edu/Image _ Datasets/Caltech101/.
[7]EVERINGHAM M,VAN GOOL L,WILLIAMS C K I,et al.Pascal VOC data sets [DB/OL]. [2014 -02 -15]. http://pascallin. ecs. soton. ac. uk/challenges/VOC/.
[8]RAMISA A,ALDAVERT D,VASUDEVAN S. The IIIA30 mobile robot object recognition dataset[C]∥11th International Conference on Mobile Robots and Competitions (ROBOTICA 2011). Lisbon:[s. n.],2011:72 -77.
[9]ZENDER H,MOZOS O M,JENSFELT P,et al. Conceptual spatial representations for indoor mobile robots[J]. Robotics and Autonomous Systems,2008,56(6):493 -502.
