基于运输网络的配送路线优化模型

张艳伟，周 万，向家伟

(1.武汉理工大学 物流工程学院，湖北 武汉430063;2.武汉理工大学 计算机科学与技术学院，湖北 武汉430063)

解决物流配送路线优化问题的方法有很多，常用的有旅行商法、动态规划法、节约法、扫描法、分区配送法、方案评价法等［1］。相关研究中，王会云等［2］研究了旅行商法在配送路线优化问题中的应用，并利用Matlab 和遗传算法对该问题进行了求解。陈彦军等［3］利用旅行商模型研究了物流配送问题。王勇等［4］利用动态规划法对配送路线及配送时间的优化问题进行了研究分析。张学志等［5］提出了一种改进节约算法，并利用该算法对配送路线问题进行了研究。杨文霞等［6］采用改进扫描算法解决配送路线优化问题，并结合实际案例分析了该优化方法的工作性能。霍亮［7］利用分区配送法研究了基于GIS 的物流配送问题。此外，文献［8 -11］研究了相关智能优化算法在配送路线优化问题中的应用，包括免疫算法、遗传算法、禁忌搜索算法和模拟退火算法。WANG 和LU［12-13］研究了利用遗传算法及其改进算法求解具有容量限制的路径优化问题，其基本思想是将遗传算法与其他算法(例如扫描法)相结合，用来改进算法的求解质量及计算速度。LEUNG 等［14］将二维装箱问题及配送路线问题结合起来考虑，并采用模拟退火算法对该问题进行求解，而针对同一问题，FUELLERER 等［15］则考虑采用蚁群算法进行求解。LIN 等［16］采用了一种模拟退火算法与禁忌搜索算法的混合算法对容量限制的路径规划问题进行求解，并通过大规模的算例实验验证了算法的有效性。LECLUYSE等［17］考虑了更加复杂的情况，如考虑了行程时间会随时间随机变化的车辆路径问题，并对行程时间可靠性进行了分析。由于客户需求可能产生在区域内的任意位置，确定出客户与配送中心以及客户之间的最短运输距离就十分必要。传统的配送优化模型往往假设配送中心及各客户之间的运输距离为两点之间的直线距离，并简单地利用勾股定理进行计算，这导致模型的优化结果与实际最优路线相差甚远。因此，在对配送路线进行优化时，必须考虑运输网络对配送计划的影响。

1 配送优化模型

考虑到客户与配送中心以及客户之间行车距离在实际配送中的重要性，将配送优化问题描述为：配送中心负责某一特定区域内的货物配送任务，满足该区域内随机产生的客户需求，需要确定配送方案，使送货车辆行走的总路程最短。结合配送问题的实际运作，建立如下数学模型：

目标函数：约束条件：

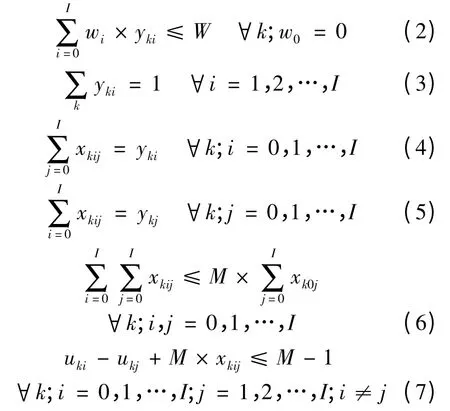
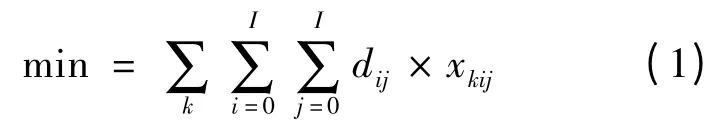
模型中各数学符号的意义如下：

I为需求点的数目;i为需求点编号，i=1，2，…，I，i=0 为配送中心编号;W为配送车辆的容量上限;wi为需求点i的货物需求量，i=1，2，…，I;k为配送路线序号;dij为点i到点j的运输距离(受运输网络限制的最短路程)，i，j=0，1，2，…，I;M为一个较大的整数。

决策变量：

yki为当配送路线k满足客户i的需求时，yki=1，否则，yki=0;xkij为当配送路线k满足i和j的需求，且j的访问顺序紧随i之后时，xkij=1，否则xkij=0;uki为0 -1 变量，用于消除配送路线模型中可能产生子回路的情况。

目标函数式(1)表示多条配送路线的总路程最短;约束条件式(2)表示单条配送路线装载的货物必须小于配送车辆的容量上限;约束条件式(3)表示客户需求有且只有一条配送路线为其服务;约束条件式(4)和式(5)保证了配送路线进出需求点的流量平衡;约束条件式(6)限定只有从配送中心出发的回路才是有效的配送路线;约束条件式(7)用来消除可能存在的子回路。

2 运输距离矩阵

由于客户需求是在特定区域内随机产生的，考虑到运输网络的限制，不能简单地用两点之间的直线距离作为运输距离。图1 为某实际的运输网络，0 为配送中心所在位置，位置固定，1 ～10 为客户所在位置(客户所在位置位于既定路网)，在绝大多数情况下，两点之间没有直线道路连接，且由于运输网络较为复杂，当两个点相距较远时，可供选择的路径较多，两点之间的最短路程很难通过观察得知。

针对实际运输网络中任意两点之间最短路程未知的情况，笔者采用弗洛伊德算法计算不同点之间的最短路程。在利用弗洛伊德算法进行计算时，首先需要将运输网络转化为一个距离矩阵，该矩阵包含了运输网络的所有空间信息。对于如图1 所示的运输网络，需要对其中所有的节点(即实际交通网络中所有的丁字路口和十字路口)编排序号。此外，配送中心和各客户需求点也需要编排序号。

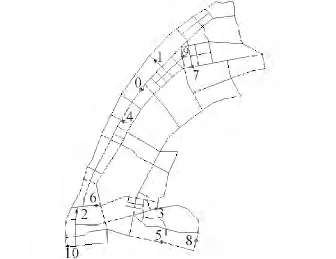
图1 实际运输网络示意图

用G(V，E)表示如图1 所示的无向连通图，用vi表示点i，(vi，vj)表示连接i和j的弧，d(vi，vj)表示弧的长度。图1 中共有101 个路口，1 个配送中心和10 个客户需求点，则需要构建一个112 ×112 的初始距离矩阵D(0)={a(0)ij}112×112。

当运输网络中的两点之间有弧直接连接时，弧的长度即为初始距离矩阵中对应元素的值;当两点重合时，对应元素(矩阵主对角线上的元素)的值为零;当两点不重合且没有弧直接连接时，初始矩阵中对应元素的值则为无穷大，在进行运算时，取一个足够大的整数M即可。

对于k=1，2，…，n，计算：

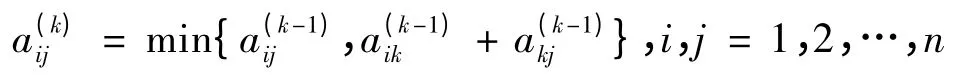
当k=n时，D(n)={a(n)ij}112×112为任意两点之间的最短路程。利用LINGO 能够方便地实现弗洛伊德算法，可以将初始距离矩阵D(0)从EXCEL导入到LINGO，求解结果则可以从LINGO 导入到EXCEL。对于如图1 所示的运输路网，可以在3秒之内求出最短路程矩阵，该矩阵即为配送路线优化模型中需要的距离矩阵。LINGO 中的程序代码如下所示：

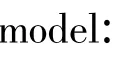
最短运输距离矩阵的求解结果如表1 所示，可以发现运输距离矩阵是对称矩阵，该距离矩阵将作为后续配送路线优化的输入量。

表1 运输距离矩阵

3 LINGO 算例分析

利用上述求最短路程矩阵的方法和建立的整数线性规划模型，可以对配送路线问题的算例进行求解。利用图1 中随机生成的10 个客户点，设配送车辆的容量上限为24，随机生成10 个客户点的需求量，这些需求量为3 ～8 之间的整数，且服从均匀分布，如表2 所示。

表2 客户点的货物需求量

利用LINGO 及相关数据，可以求出该算例的最优解，在一般笔记本电脑上的求解时间为38 min。LINGO 中的程序代码如下所示：

其中，路线1 完成的货运量为21，路线2 为17，路线3 为15。最优解下的目标函数值为30.736(地图上距离)。需要注意的是，在定义路线集合时无法精确预知最优条件下的配送回路个数。为此，在LINGO 编程时，综合考虑车辆容量和客户点总需求量，路线集合元素设置为一个足够大的值。算例中设置为4 个，大于最优解的配送回路个数(3 个)，设置合理。

4 模拟退火算法求解

模拟退火算法是一种基于蒙特卡罗迭代求解策略的随机寻优算法。模拟退火算法与初始解状态无关，具有渐进收敛性。模拟退火算法的求解流程如图2 所示。

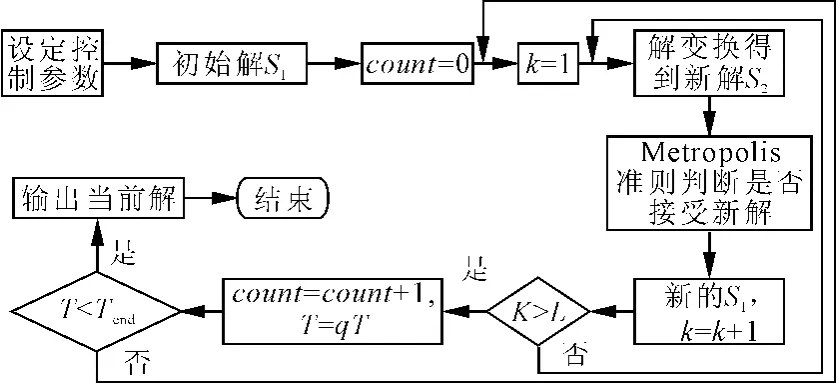
图2 模拟退火算法流程图

模拟退火算法的功能模块主要包括：设置控制参数，生成初始解，变换生成新解，Metropolis 准则和降温模块［18］。其中控制参数的设置对算法的求解质量有较大影响，主要控制参数包括初始温度、降温速率、迭代步长和终止准则(笔者限定温度下降次数超过500 次时停止运算)。

利用C 语言编写配送路线优化问题的模拟退火算法程序，对算例进行多次求解。通过多次试验得到求解质量较高的算法控制参数，如表3所示。在设定的控制参数下，随机运行程序12次，由于程序以降温次数作为终止准则，在一般笔记本电脑上程序每次的运行时间为9.89 s，记录每次试验的运行结果，包括目标函数值以及首次得到该函数值的降温次数等，如表4 所示。从表4 可以看出，算法程序在12 次试验中，有6 次收敛到了全局最优解，5 次收敛到相对误差仅为0.228%的局部最优解，最差的局部最优解为第9次试验结果，相对误差也仅为0.309%。

表3 模拟退火算法参数设置

LINGO 及模拟退火算法的求解结果表明，模拟退火算法能够有效地解决所提出的路线配送优化问题。笔者利用弗洛伊德算法和模拟退火算法对配送路线优化问题进行求解，得到的配送路线图更加符合配送活动的生产实际，如图3(a)所示。相关文献由于没有考虑运输网络的约束，配送路线的优化结果通常如图3(b)所示。

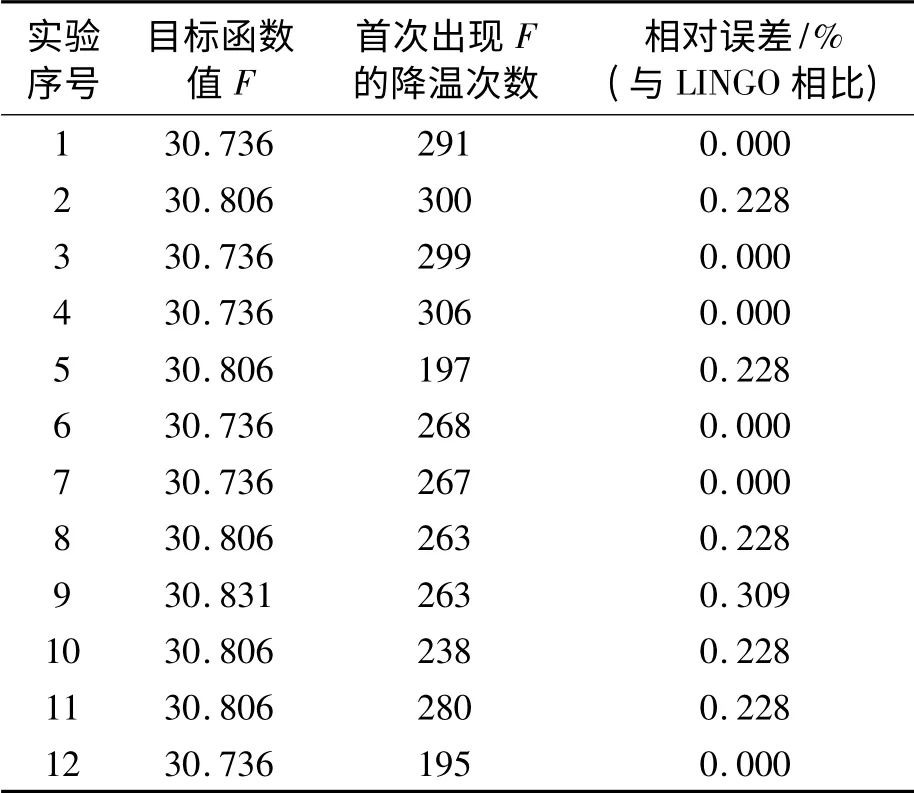
表4 算法程序试验结果

图3 路线优化结果对比

5 结论

笔者基于实际运输网络考虑物流配送路线优化问题，针对运输距离受限于运输网络，而不能简单利用勾股定理以直线距离作为运输距离的实际情况，利用弗洛伊德算法以及LINGO 和EXCEL软件计算运输网络中任意两点之间的最短路程，并以此构造配送路线优化模型中的距离矩阵。利用求得的运输距离矩阵以及所提出的用于解决配送路线优化问题的整数线性规划模型，可以在LINGO 环境下对小型算例进行求解，求解结果证明，该整数线性规划模型正确，能够用于解决配送路线优化问题。

考虑到LINGO 求解速度较慢的弱点，开发了基于C 语言的模拟退火算法程序对相应的配送路线优化问题进行求解，求解结果显示，在合适的控制参数条件下，模拟退火算法能够得到相对误差较小的优化解，并且算法求解时间相对于LINGO 精确求解具有较大的优势。

［1］CHEN W，EBERHART R C. Genetic algorithm for logistics scheduling problem［M］.［S.l.］：IEEE Press，2002：512 -516.

［2］王会云，肖建禄，刘登泰，等. 基于遗传算法的配送路线优化［J］.后勤工程学院学报，2008，24(3)：91-94.

［3］陈彦军，吴国平，李敬民. 基于GIS 空间分析的物流配送模型研究及应用［J］.南京师范大学学报：工程技术版，2004，4(3)：68 -72.

［4］王勇，池洁. 物流配送路线及配送时间的优化分析［J］. 重庆交通大学学报：自然科学版，2008，27(4)：647 -650.

［5］张学志，陈功玉. 车辆路线安排的改进节约算法［J］.系统工程，2008，26(11)：67 -70.

［6］杨文霞，郭海湘，杨娟，等.改进的扫描法求解单车场多车型车辆路径问题［J］. 物流技术，2010，21(4)：50 -53.

［7］霍亮.基于GIS 的物流分区配送方法研究［J］.测绘学院学报，2003，20(2)：145 -147.

［8］张彦敏，芮小平. 用免疫遗传算法实现配送路线求解［J］.武汉理工大学学报，2011，33(9)：72 -76.

［9］黄明，林广智，梁旭，等.改进的遗传算法在车辆路径问题中的应用［J］. 大连交通大学学报，2010，31(1)：95 -99.

［10］郎茂祥，胡思继.车辆路径问题的禁忌搜索算法研究［J］.管理工程学报，2004，18(1)：81 -84.

［11］杨宇栋，郎茂祥，胡思继.有时间窗车辆路径问题的模型及其改进模拟退火算法研究［J］.管理工程学报，2006，20(3)：104 -107.

［12］WANG C H，LU J. An effective evolutionary algorithm for the practical capacitated vehicle routing problems［J］. Computers ＆ Operations Research，2010，37(11)：1870 -1876.

［13］WANG C H，LU J. A hybrid genetic algorithm that optimizes capacitated vehicle routing problems［J］. Expert Systems with Applications，2009(36)：2921-2936.

［14］LEUNG S C H，ZHENG J. Simulated annealing for the vehicle routing problem with two - dimensional loading constraints［J］. Flexible Services and Manufacturing Journal，2010，20(1 -2)：61 -82.

［15］FUELLERER G，DOERNER K F，HARTL R F，et al.Ant colony optimization for the two - dimensional loading vehicle routing problem［J］. Computers ＆Operations Research，2009，36(3)：655 -673.

［16］LIN S W，LEE Z J，YING K C，et al. Applying hybrid meta - heuristics for capacitated vehicle routing problem［J］. Expert Systems with Applications，2009(36)：1505 -1521.

［17］LECLUYSE C，WOENSEL T V，PEREMANS H.Vehicle routing with stochastic time-dependent travel times［J］.40R - Q J Operations Research，2009(7)：363 -377.

［18］史峰，王辉，郁磊，等. Matlab 智能算法30 个案例分析［M］.北京：北京航空航天大学出版社，2011：178 -187.