基于相空间重构及自适应支持向量机的短期风速预测

杨洪深

风速的随机性对风电场输出功率具有显著影响，通过风速预测，可在一定程度上降低风能的间歇性对电网的不利影响[1]。风速常见的预测方法主要包括时间序列法[2]、神经网络法[3]、支持向量机法[4]、卡尔曼滤波法[5]等。在众多预测模型中，支持向量机（Support Vector Machine，SVM）与神经网络不同，是一种建立在结构风险最小化原则基础上的预测模型，具有更优越的推广能力，通常被应用于分类及回归等模式识别领域。

SVM用于风速预测的难点在于模型参数的确定及输入向量的选择。文献[6]指出了风速的变化是空气动力学演化的结果，空气动力学系统属于混沌系统，因此风速时间序列具有混沌特性，并采用加权零阶局域法预测风速，取得了较好的预测效果。实际上，SVM和混沌理论中的相空间重构都把输入空间的向量扩展到高维空间，挖掘系统隐含的规律。因此，相空间重构如果能够利用SVM理论，自动地通过非线性变换把输入空间的时间序列映射到高维空间，并在这个空间实现数据的线性可分，提取其系统内部隐含的信息，可以更好地实现混沌时间序列的预测。据此，文章在风速时间序列相空间重构的基础上采用自适应支持向量机[7]，对SVM模型参数进行自适应调整，从而获得较高的预测精度。

1.风速序列混沌属性分析及相空间重构

1.1 风速序列混沌属性分析

混沌系统产生的轨迹经过一段时间的变化之后，最终会在高维空间呈现出具有一定规律的运动轨迹，称为混沌吸引子。高维度空间的混沌吸引子经过拉伸、折叠后成为低维空间中的混沌时间序列，并表现出混乱复杂的特性。

通常的预测方法仅针对这种复杂、无序的时间序列展开，难以揭示出其内在演化规律，预测精度受到限制。混沌时间序列的预测可以理解为动力系统研究中的“反问题”，即给定相空间的一串迭代序列，如何构造一个非线性映射来表达这一动力系统。其理论基础是Takens的嵌入定理[8]和相空间重构理论[9-11]。

风速可以看成是空气动力学混沌系统的一个分量，其变化过程是气压、温度、湿度等多因素影响的结果，通过对混沌吸引子的恢复可以找到风速时间序列的内在变化规律，从而实现对风速的短期预测。

1.2 相空间重构

Takens指出了相空间重构的思想：设d是动力系统的维数，如果延迟坐标的维数 ，则在这个嵌入维空间里可以把有规律的轨迹恢复出来。对于时间序列x1，x2，…，xN-1，xN，将其嵌入到 m 维欧式空间 Rm中，则得到相空间重构的相点：

1.3 延迟时间的计算

延时时间 的选择方法主要有自相关法、平均位移法、去偏复自相关法、互信息法等[10]。自相关函数法是一种通过提取时间序列间的线性相关性来计算延迟的简单方法。设时间序列数目为N，则序列的时间跨度为时的自相关函数为：

利用互信息法可以估计时间延迟。一个时间序列的互信息可以表示为：

式中 为概率， 是两个时间序列 和的互信息函数， ，用来表示两者相关性的强弱，越小，时间序列的相关性越弱，但是相关性太弱又会导致系统性态的不确定，所以延迟时间不能过大，因此将第一次达到极小值时的时滞作为相空间重构的时间延迟。

文章算例中综合考虑自相关函数法和互信息法确定延迟时间。

1.4 嵌入维数的计算

嵌入维数的确定方法有几何不变量法，Cao算法，假近邻法等。文章采用假近邻法确定最佳嵌入维。

1.5 最大Lyapunov指数计算

混沌具有三个明显的特征：（1）对初始条件具有敏感的依赖性；（2）非周期性；（3）存在奇怪吸引子。判定一个系统是否混沌的常用方法主要有Lyapunov指数法及连续功率谱法等。Lyapunov指数是对相空间中初始条件不同的两条相邻的轨迹随时间推移按指数规律分离的比率的定量描述，若最大Lyapunov指数大于零，则可判断该序列是混沌系统。最大Lyapunov指数的计算步骤可参考文献[12]，文章采用此方法计算最大Lyapunov指数来判断风速的混沌属性。

2.自适应支持向量机(Self Adaptive SVM—SA-SVM)

支持向量机应用于回归方面，主要有Vapnik提出的ε-回归支持向量机（ε-SVR），其基本算法详见文献[13-14]。支持向量机模型中，不敏感系数ε、惩罚因子C和核函数宽度系数σ2等参数对模型的推广能力和预测性能具有较大的影响，交叉验证法虽然能在一定程度上确定最佳参数，但计算量大、速度慢[15]。文章采用参数自适应调整法确定SVM模型参数。该方法根据模型训练过程中的误差变化情况，自动地调整支持向量机的参数，以获得较好的回归估计函数。

设惩罚因子和宽度系数的调整步长为△C和△σ2，且不敏感系数ε取值为ε＝0.5D，其中D为噪声分布函数的方差，在整个迭代过程中ε保持不变。

以ME最小化为目标的C和σ2自适应调整步骤如下：

（1）设迭代初值k=0，并选定参数的初值。宽度系数的初值为其中x为输入向量的均值，即；惩罚因子的初值为：C（0）＝2（max（yi）-min（y）i）。利用参数初值进行支持向量回归估计，并求得平均拟合相对误差 ME（0）。

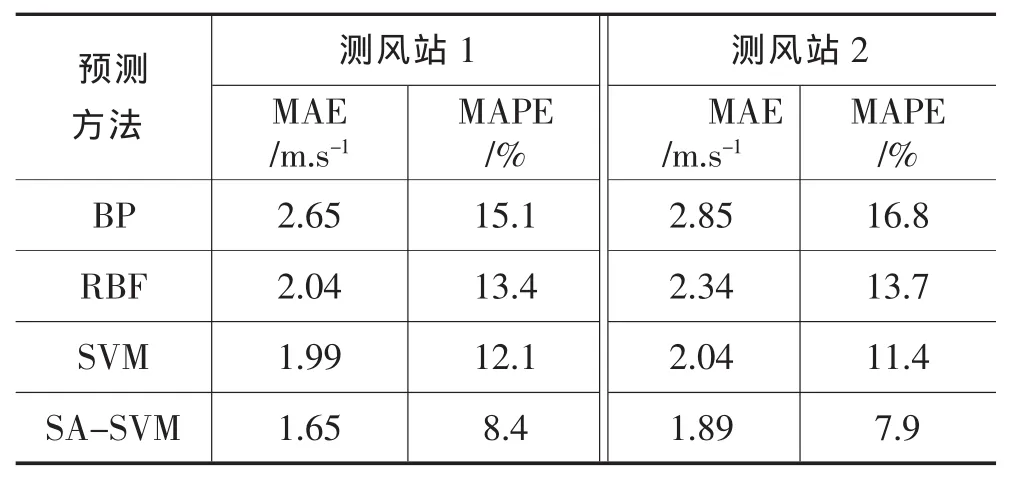
（3）判断 ME（k+1）

（5）记回归精度为 ，判断 是否成立，若不成立，则转到步骤（2）；若成立，则转到步骤（6）。

（6）判断回归函数是否过于复杂，即检查回归函数在相邻样本中值点是否落在yi和yi+1之间，若未落在yi和yi+1之间，则回归函数过于复杂，同时迭代次数没有达到最大次数，则令并转到步骤（4）；否则，回归函数不复杂，转到步骤（7）。

（7）迭代终止，以当前函数作为回归函数。

3.风速预测

根据前文提出的方法，采用自适应支持向量机对风速进行混沌预测的步骤如下：

(1)根据混沌相空间重构理论计算风速样本的最佳嵌入维数d和延迟时间 ，生成训练样本数据集和测试样本数据集，并对样本数据作归一化处理。

(2)采用SA-SVM方法训练支持向量机，并自适应调整模型参数从而得到回归函数。

(3)利用训练好的支持向量机模型预测风速。

实验数据取自某风电场2012年5月份的小时风速历史数据。将历史风速数据分别划分成2个数据集，即训练数据集和测试数据集，对各数据集进行相空间重构构造样本（Xt,Yt）。前者用于对网络进行训练，后者用于检验网络的预测性能。

采用平均绝对误差 (MAE)、平均绝对百分比误差(MAPE)和均方根误差（RMSE）来对预测效果进行评价。即：

其中，N为样本个数，WR为实测值，WF为预测值。

图1的自相关函数曲线第一个经过1-1/e的延迟时间为4h，第一个过零点的延时为21h；图2是由互信息法计算结果，发现 第一次达到最小值的时延也近似为4h。图3是风速序列在不同延迟下的相空间三维轨迹，混沌系统包含较为丰富的信息，混沌吸引子的相空间轨道随着时间延迟的变化而变化，较小时，相轨线被压缩在对角线上，吸引子所包含的信息量较少，增大后相轨线逐渐展开，当超过一定值后，相轨线开始折叠，吸引子所包含的信息量也开始减少；可见 ＝1时，吸引子相邻点的相关性太强，吸引子包含的信息较少，＝10,20时吸引子在相空间中趋向于均匀分布，类似于随机时间序列，短期预测性消失；综合考虑取时间延迟为4h。图4为由假近邻法确定的最佳嵌入维m=5。风速时间序列的最大Lyapunov指数计算值为0.0301，证明了风速序列具有混沌特性，可以采用混沌预测方法。

图1 自相关函数法求延迟时间

图2 互信息法确定延迟时间

图3 不同延迟时间对应的混沌吸引子

图4 假近邻法确定的最佳嵌入维

为综合比较考察文章方法的预测性能，将SA-SVM与BP网络进行对比分析。图5是预测曲线，表1是十次试验误差均值。

图5 预测曲线

表1 预测误差

从图5和表1看出，SA-SVM的预测曲线相对于BP神经网络更接近于实测值，并且在风速突变点，SA-SVM的预测误差更小。SA-SVM预测模型的误差指标MAE、RMSE分别为2.42m/s和4.27m/s，两项误差指标均小于BP神经网络。SA-SVM法在371h和389h等风速突变点处的预测误差明显大于其他时刻，这是由于风速发生了较大波动时，其对应的相点与预测中心相点间的关联度较低，从而得到的预测误差较大。

将文章所提SA-SVM风速预测方法及BP神经网络、RBF神经网络、SVM同时应用于某风场2个测风站的风速预测。各方法预测误差十次实验平均值如表2所示。可以看出，对2个不同测风站，SA-SVM的预测误差最小，这进一步说明该方法表现出良好的稳健性和预测精度。

表2 预测方法比较

4.结论

文章分析了风速时间序列的混沌属性，并进行相空间重构。采用自适应支持向量机模型进行短期风速预测研究,取得了较高的预测精度。其原因一方面在于混沌系统相空间重构理论与SVM都是把输入空间的向量扩展到高维空间，并提取系统隐含的信息和规律；另一方面在于参数自适应调整能够为SVM获得优良的回归估计性能。

［1］杨秀媛，肖洋，陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报，2005，25(11)：1-5.

［2］孙春顺，王耀南，李欣然.小时风速的向量自回归模型及应用[J].中国电机工程学报，2008，28(14)：112-117.

［3］Li Shuhui，Wunsch D，O'Hair E，et al.Using Neural Networks to Estimate Wind Turbine Power Generation[C].//IEEE Power Engineering Society WinterMeeting.Columbus，USA：Power Engineering Society，2001：977-986.

［4］杜颖，卢继平，李青，邓颖玲.基于最小二乘支持向量机的风电场短期风速预测[J].电网技术,2008,32(15):62-66.

［5］潘迪夫，刘辉，李燕飞.基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J].电网技术，2008，32(7)：82-86.

［6］罗海洋，刘天琪，李兴源.风电场短期风速的混沌预测方法[J].电网技术，2009，33(9)：67-71.

［7］田景文，高美娟.人工神经网络算法研究及应用[M].北京：北京理工大学出版社，2006.7.

［8］Taken S F.Detecting Strange Attractors in Turbulence[J].Lecture Notes in Mathematics,1981,898:366-381.

［9］陈铿，韩伯棠.混沌时间序列分析中的相空间重构技术综述[J].计算机科学，2005，32(4)：67-70.

［10］陶佳，张弘，朱国荣,等.基于优化相空间重构技术的风电场发电功率预测研究[J].中国电机工程学报，2011，31(28)：9-14.

［11］王丽婕，廖晓钟，高爽等.并网型大型风电场风力发电功率-时间序列的混沌属性分析[J].北京理工大学学报，2007，27(12)：10 77-1080.

［12］Wolf A.Determining Lyapunov Exponents From a Time Series[J].Physica D:Nolinear Phenomena,1985,16(3):285.317.

［13］Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag，1995.

［14］Chen Bojuen,Chang Mingwei,Lin Chihjen.Load Forecasting UsingSupportVectorMachines:aStudyon EUNITE Competition 2001[J].IEEE Transactions on Power Systems,2004,19(4):1821-1830.

［15］邓乃扬，田英杰.数据挖掘中的新方法——支持向量机[M].北京：科学出版社，2004.