中等收入及其人口比重测算方法研究

朱 玲

1.引言

我国现在处在典型的中等收入国家发展阶段，对于中等收入的定义各不相同，一般以收入的多少为标准，划分中等收入者。国内经济学专家对中等收入者的概念、界定方法和标准，都有不同的见解。其中在顾纪瑞（2005）[1]的综述中，主要有三种标准来定义中等收入者：（1）中等收入主要不看消费水平和财产的多少，而看持续的收入能力;(2)中等收入者的起点略高于人均GDP，接近职工年平均工资水平，上限则定在起点的4倍;(3)以预测的2020年人均年收入作为现阶段中等收入标准的基础。

用绝对收入水平对中等收入者下定义各有利弊。可以比较准确地测算中等收入者的人数及其所占的比重，但是主观成分较大（上下限都比较难确定）；用统一的上下限标准测算中等收入群体比例，存在很大难度。其实，如果我们关注的重点不是中等收入群体的具体特征，而是中等收入群体比重本身，则有另外两种方法可供参考，收入空间法和人口空间法，也是现在用的比较多的方法。但是这两种方法在一定程度上也都有各自的缺陷，文章提出的两种测算方法主要是对这两种常用方法的改进。

2.收入空间法缺陷及其改进

2.1 收入空间法的缺陷

收入空间法定义：收入落在中位收入m的一个范围内的人口为中等收入人口。 如图1，中等收入人口是收入属于（xl，xh）中的人口，这时中等收入人口比例M等于F(xh)-F(xl)，见图2。这种方法中xl与xh的取法具有任意性，由于经济进步，通货膨胀等因素的影响，收入的区间是变化的，更多的情形是所有人口的收入都提高了，即全社会的收入区间右移，可见xl与xh的任意性使纵向比较各年的中等收入人口时出现困难。为了克服收入空间法中xl与xh的任意性以及中等收入区间取法的任意性，我们研究了确定中等收入范围的科学方法。

图1 收入空间法

图2 中等收入人口比例

2.2收入空间法的改进

收入分配经验分析说明，收入分配曲线一般是右偏的，如果高收入人群比例较大，由于均值受极端值影响较大，则人均收入变大，均值就会远离中位数值，中等收入人群比例就会下降，可见收入分布的偏度影响中等收入的范围。人口收入分布偏度记为：

其中m代表中位收入，u代表平均收入，若skewnss值越大，则人口收入分布偏度越大，若skewnss值越小，则人口收入分布偏度越小。

为了确定中等收入范围，考虑到中位数的统计学意义，我们以中位数左边的值xl记为中等收入的下限，中等收入右边的点xu记为中等收入的上限，我们建立这样的函数关系：

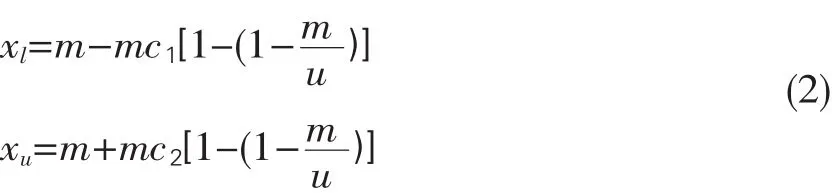
中等收入群体是一个国家或地区在一定时期内收入水平处于中间范围内的所有人员的集合，在不考虑收入分布偏度的情况下，Thurow(1984)选择中位数的75%到125%范围内的群体作为中等收入群体。文章在研究中等收入范围时考虑收入分布偏度，取c1=c2=，这样即可求得中等收入的范围为，[m(1－)，m(1+)]由上式看出，当收入分布的偏度越大，则中等收入区间变小。

记收入不高于xl的人口占总人口的比重为Pl，收入不高于xu的人口占总人口的比重为Pu，由P(x≤x)可得：

中等收入人口比例范围为：[Pl,Pu]。

构造这样的函数克服了收入区间取法的随意性了。

3.人口空间法的缺陷及其改进

3.1 人口空间法的缺陷

人口空间法考虑的是收入分配发生了变化，当中等收入范围拉大，低端人口收入下降，高端收入人口增加，直观上两极分化扩大了，这时中等收入人口应该是下降了，但是这种方法，中间的人口拥有的总收入比例不变，这与现实经济直观不符合。

3.2 人口空间法的改进

为了解决人口空间法没能解决两极分化的问题，依据参考文献[2]，引用两极分化的指数公式：

公式中m和u分别表示中位数和算术平均值，G为基尼系数，S表示50%的低收入成员的人口份额与其收入份额的差，即,S=0.5-L(0.5)，L(0.5)表示收入最低的50%的人口的收入份额。

在此基础上我们构造一个关于两极分化指数I的函数C(I)，以及构造的区间范围

同时我们借鉴这样一种思想：在正态分布的情况下，数值位于一个标准差范围的概率为68.27%，在静态的情况下，预先设定中等收入人口占总人口的比重为68.27%。这时我们可得到这样一个式子：

由于密度函数f(x)的值不易求得，因此我们换个角度求这样一个方程组从而确定C(I)。方程组如下:

其中XL、XU分别表示收入值,PL表示收入低于或等于XL的人口所占总人口的比例，PU表示收入低于或等于XU的人口所占总人口的比例，m表示中位数。

由于研究在各年中PU和PL，在合理的范围内可以取不同的值，那么这时我们可以确定一个PL，根据（3）式可以求得PU的值，接着C（I）的值也可以确定。从而中等收入的范围可以得到。同时可根据计算人口比例的变化，从而纵向研究各年中等收入人口的变动。

4.模型应用

4.1 构建新洛伦兹曲线模型

文章第二和第三部分提出的新收入空间法和新人口空间法是以洛伦兹曲线L（p）为基础。在原来的洛伦兹曲线模型的基础上构建一个新的模型使得拟合精度更高。从而使新收入空间法和新人口空间法更具有经济意义、更实用。

构建新洛伦兹曲线模型为：

我们把两个洛伦兹曲线模型[3]

与新构建的模型进行比较，分别用MSE、MAE、MAS三种标准对拟合精度的好坏进行比较①。

下表为用lingo软件计算出的MSE、MAE、MAS值。

表一 MSE、MAE、MAS 值

通过表一可以发现新构建的模型的MSE、MAE、MAS值比其他两个模型要小，说明拟合精度更高。接下来用数据对我们所构建的新收入空间法和新人口空间法以及新洛伦兹曲线进行应用。

4.2 模型应用

以下数据来自2013年全国研究生数学建模大赛E题。

题目中给出了A、B两个地区前后两个不同年份的收入分配分组数据。根据四个表的数据对各地区、各年份的中等收入的多少（或范围）、中等收入人口的数量(或范围)进行定量描述，说明中等收入人口的变化趋势。同时比较两个地区的中等收入人口、收入的变化情况。

表二 年份之一A、B两地区的中等收入的范围和中等收入人口比例的范围

表三 年份之二A、B两地区的中等收入的范围和中等收入人口比例的范围

通过比较A地区年份之一和年份之二的中等收入人口比例分别为0.2714、0.2285，能够发现第二年的中等收入人口的比例变小，两极分化严重。通过比较B地区年份之一和年份之二的中等收入人口比例分别为0.5284、0.3816，能够发现第二年的中等收入人口的比例变小，两极分化严重。

比较A、B两个地区的中等收入人口、收入，发现B地区中等收入人口比例总体大于A地区，同时B地区的中等收入的范围总体大于A地区，A地区的两极分化比B地区严重。

以上表格中的数据所用的计算方法是基于模型1，接下来我们用第二个模型 来计算，通过比较可以看出哪种模型更具优势。

通过以下方程组：

其中令 PU－PL＝68.27%， 理由是在正态分布的情况下，数值位于一个标准差范围的概率为68.27%，我们借鉴这种思想，在静态的情况下，预先设定中等收入人口占总人口的比重为68.27%。可以算得C（I），其中I是两极分化指数，I的值可以依据所给的数据不同算出不同的值，此时可以根据四组数据算出它们之间的关系，从而可以计算出两极分化指数对中等收入范围的影响，并得出中等收入人口比例的范围。根据计算结果列出以下表格：

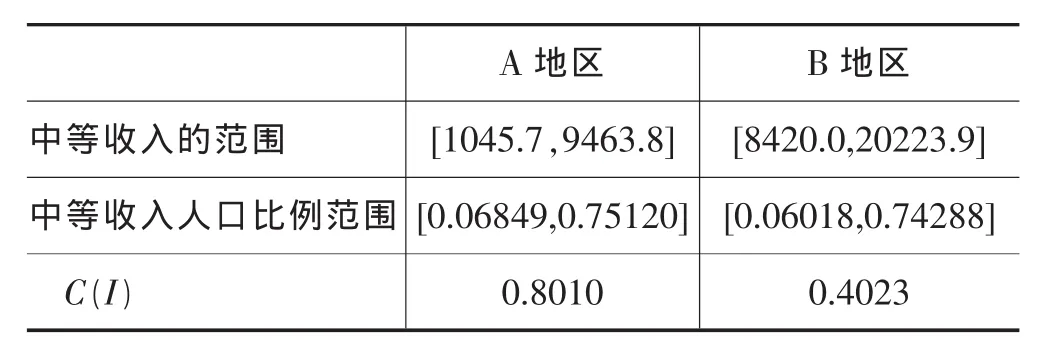
表四 年份之一A、B两地区的中等收入的范围和中等收入人口比例的范围和C（I）值

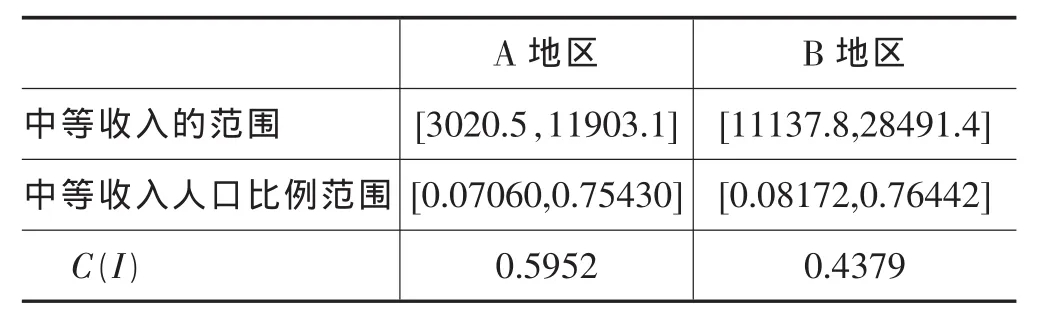
表五 年份之二A、B两地区的中等收入的范围和中等收入人口比例的范围和C（I）值

以上表格的分析结论如下：从两个表格的中等收入人口比例的范围可以发现，为了达到中等收入人口的比例为68.27%这样一个理想的状态即国家经济发展人民生活富裕大部分人处于中等收入的水平，一些低收入人群也被纳入了中等收入的群体，实际上他们没达到中等收入的水平。这与我国目前的发展不符合，此处理想化了。为了更符合我国的国情，对理想的68.27%进行修改，拟定35%为中等收入人口比例，那么计算以下方程组：

得出：

表六 A、B地区两年中等收入人口比例的范围

分析表六可以发现中等收入人口比例为35%是比较符合我国国情的，具有一定的经济意义。

5.总结

从文中改进后的方法可以看出收入空间法的改进解决了中等收入范围任意的缺陷.人口空间法的改进解决了两极分化的问题.但是两种方法仍然有改进的空间,第二种方法我们是在理想化的前提下取68.27%,但依据我国目前的国情是达不到中等收入人口比例为68.27%的.在此基础上把中等收入人口比例改进为35%,这与我们的实际相联系更具有经济意义.

注：

①此处两模型2013年全国研究生数学建模竞赛E题。

[1]顾经瑞.界定中等收入群体的概念、方法和标准之比较[J].现代经济探讨，2005，（10）：10-16.

[2]王力.均等指数和两极化指数建立与比较[J].中国人口.资源与环境，2012，（1）:149-154.

[3]Wang,Z.X.,Y-K Ng,and R.Smyth,2011.A general method for creating Lorenz curves[J].The Review of Income and Wealth 57,561-582.