酿酒葡萄和葡萄酒成分间的典型性相关分析

唐洪玉，周 琳，陈义安

(重庆工商大学数学与统计学院，重庆 400067)

酿酒葡萄和葡萄酒成分间的典型性相关分析

唐洪玉，周 琳，陈义安＊＊

(重庆工商大学数学与统计学院，重庆 400067)

根据酿酒葡萄与葡萄酒的理化指标，按“逐步降维，保留信息”的思想建立模型，把原来多个变量划为几个综合指标，并对这些综合指标进行研究，以简化问题的求解过程;因酿酒葡萄和葡萄酒质量间的内在联系及变化规律具有随机性、理化指标信息过大，先进行变量替换，分别选取15个、8个综合变量替代原变量，再对酝酿葡萄与酝酿葡萄酒主成分分析，最后进行典型相关分析。

降维;主成分分析;典型相关分析;变量替换

目前，对葡萄酒的鉴别主要采用感官评定法。传统的产品感官评价主要依靠品评专家的个人经验来完成，品评专家必须具有大量的行业背景知识和丰富的品评经验。但品评结果的主观性较强，且品评过程时间长，费用大，成本较高，不利于大批量样本的感官品评。由于葡萄酒的化学成分复杂，也可借助化学计量学的方法对其进行区分。化学计量学方法即通过定量分析葡萄酒中多种化学物质的含量，再对数据进行多元统计分析，从而达到对样品进行鉴别的目的。这种方法比感官评定更加客观、公正。葡萄酒作为许多欧洲国家的一种重要的商品，国外对这种鉴别方法已经作了较多的研究。但是，对化学成分进行准确的定性定量分析较困难且过程复杂。葡萄酒的成分有1 000多种，并且它们之间存在着复杂的关系。因此，采用科学的方法使存在于这些复杂关系的问题简单化，进而更加清楚地了解它们之间的关系，多元统计方法无疑可以为葡萄酒的质量控制、预测、预报、区分提供一种有效的途径。多元统计分析中主成分分析和典型性相关分析数学工具能把众多的描述语转化为较少的、综合性较强的描述语，并且能够反映出原来多个描述语的信息，从而筛选出科学合理的描述特性。

1 问题的分析

考虑到酿酒葡萄与葡萄酒的理化指标数量过多，利用主成分分析的降维思想，寻找少数几个综合变量(原变量的线性组合)对替代原变量，将原两组变量的关系化为少数几对综合变量的关系。于是分别建立酿酒葡萄与葡萄酒的理化指标的向量矩阵，由于指标信息大，于是对它们进行了变量替换，并建立了典型性相关分析模型;应用Matlab软件先对酝酿葡萄与酝酿葡萄酒进行主成分分析，分别选取与主成分个数相同的综合变量替代原变量，然后再进行典型相关分析。

2 基本假设

(1)两组评酒员对葡萄酒的质量评估是权威公正的，不掺杂个人情感因素。

(2)在酝酿葡萄过程中，每种样品的原材料不发生替换。

(3)酿酒葡萄、葡萄酒的各种指标测量值是完全可信的。

(4)葡萄酒的质量只与外观、香气、口感、平衡整体有关。

(5)假设每一个样品酒源自同一个品酒组的平均评分都是来自同一个总体的样本，服从正态分布，且每个总体之间相互独立。

(6)假设两个品酒组分别对红葡萄酒、白葡萄酒的品均分具有方差齐性，若用σ21表示甲组品酒员给每个红葡萄酒样品平均分的方差，σ22表示乙组品酒员给每个红葡萄酒样品平均分的方差，即:σ21=σ22。

3 符号定义

Xj:表示红葡萄酒第j个指标的值(j=1，2， 31);Xij:表示红葡萄酒的第i个品种的第j个指标值;zk:为红葡萄酒新的指标值(k＜j);A:标准化后的红葡萄的典型相关系数;B:标准化后的白葡萄的典型相关系数; R:酿酒红葡萄和红葡萄酒的理性指标之间的相关性。

4 模型建立

酿酒葡萄与葡萄酒的理化指标之间的联系，表面上无法看出它们的关系。但酿酒葡萄、葡萄酒的理化指标均可以建立向量矩阵，于是考虑从这两个向量矩阵间寻找关系。典型性相关分析［1］是研究两组变量相关关系的一种统计方法，它的思想与主成分分析模型［2］相类似，以“逐步降维，减少变量”的思想为中心，寻找几个综合变量来替代原有的多个变量，与本题所要解决的问题相融合，于是建立典型性相关分析模型。

首先，对酝酿葡萄与葡萄酒进行主成分分析，分别选取15个与9个综合变量替代原变量进行典型相关分析［1］。设研究的酝酿葡萄与葡萄酒的两组指标变量分别为 X=(χ1，χ2， χp)T，(p=15);Y= (y1，y2， yq)T，(q=9)。分别对X、Y的每个指标，观察n次，有:

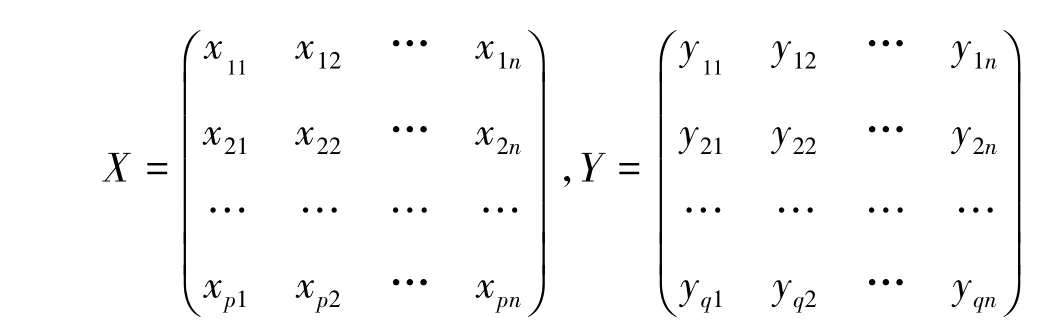
分别对X，Y取行平均，得到样品向量的平均值:

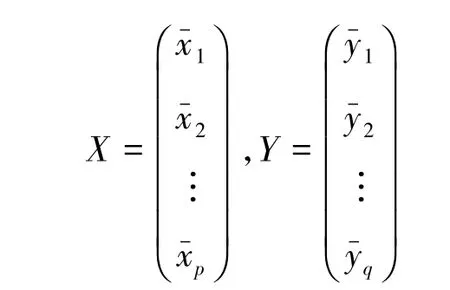
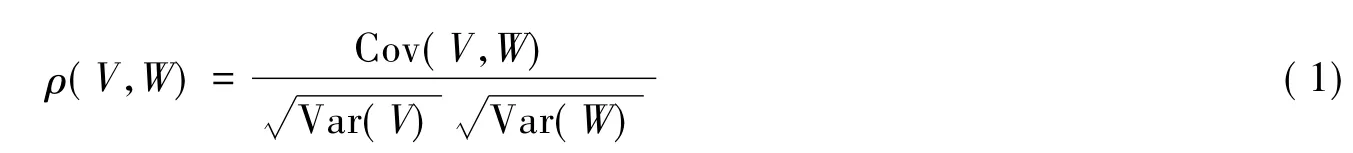
分析式(1)将发现:在使得V，W的相关达最大的同时，V和W的方差将达最小，这说明按此准则得到的典型成分V和W，对原变量组X和Y的代表性最差，它们无法更多地反映原变量组的变异信息。另一方面，因V，W任意线性组合的相关系数与V，W的相关系数相等，便使得相关系数最大的V=a'X和W=b'X并不唯一。故在典型相关分析解法［4］中附加了约束条件:

接下来，在约束条件式(2)下，求出a、b，使得ρ(V，W)最大。于是做拉格朗日函数［5］:

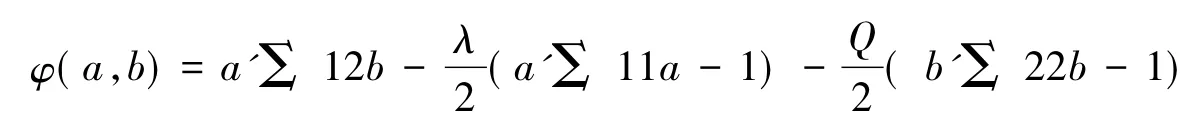
对a求导:

对b求导:

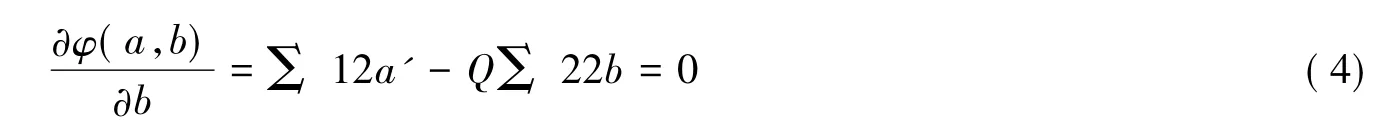
再式(3)×a'，式(4)×b'得:

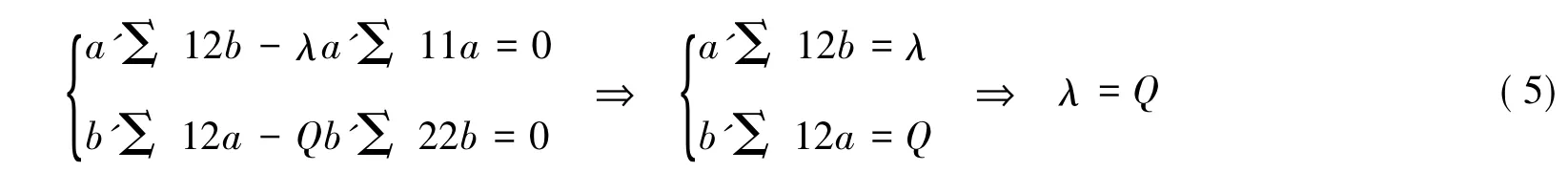
而a'Σ 12b正是相关系数ρ(V，W)，利用式(4)中的结论，可得:

由式(7)得:

将式(8)代入式(6)中，得:

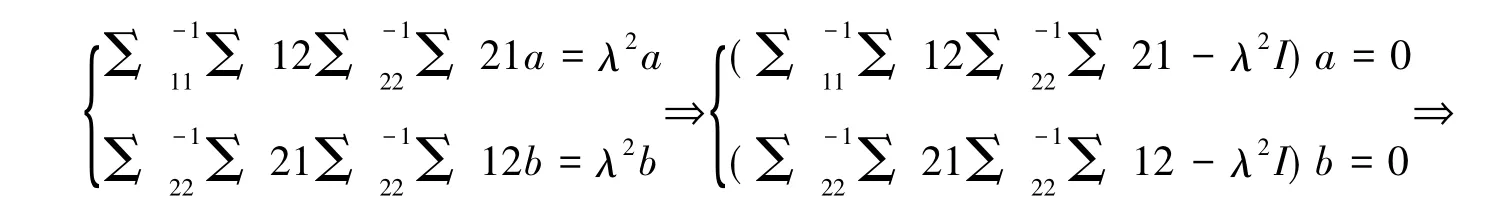
由定义可知a'X，b'Y是X，Y的第一对典型相关变量，它们之间的相关系数称为第一个典型相关系数。

最后利用MATLAB软件［6］求出第一典型变量和典型相关系数。

5 模型的求解

5.1 主成分分析

采用主成分分析方法，先将酿酒葡萄的理化指标进行主成分分析，得到了红白酿酒葡萄的15种主要相关成分，分别是氨基酸总量、花色苷、多酚氧化酶活力、DPPH自由基、总酚、单宁、葡萄总黄酮、总糖、还原糖、可溶性固形物、可滴定酸、固酸比、干物质含量、果皮质量和果皮颜色;对于葡萄酒的理化指标，用同样的方法得到两种葡萄酒的理化指标的主要相关成分，其中红葡萄酒的成分是花色苷、单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积和色泽;白葡萄酒的成分是单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积和色泽。

5.2 典型性相关分析

第二步先将酿酒红葡萄和红葡萄酒进行典型相关性分析，利用matlab软件，使用指令［A，B，R］= canoncorr(χ，y)，分别得到了矩阵A、B和R，其中A和B为标准化的红葡萄、白葡萄的典型相关系数，酿酒红葡萄和红葡萄酒的理性指标之间的相关性为R，如表1、表2所示。

表1 酿酒红葡萄和红葡萄酒的理化指标之间的相关性

由表1可以看出花色苷、单宁、总酚、酒总黄铜和白藜芦醇相关性极强，DPPH、色泽L*和色泽a*相关性较强，色泽b*相关性较小，可以忽略。同样的得出了酿酒白葡萄和白葡萄酒的理性指标之间的相关性R:

表2 酿酒白葡萄和白葡萄酒的理化指标之间的相关性

由表2可以看出单宁、总酚和酒总黄铜相关性极强，白藜芦醇、DPPH和色泽L*相关性较强，色泽a*和色泽b*相关性较小，可以忽略。

［1］王俊，谢晓佳.基于层次分析法及可拓理论的露天采石场安全评价研究［J］.重庆工商大学学报:自然科学版，2013(6): 61-68

［1］高惠璇.典型相关与典型冗余分析［J］.数理统计与管理，2002(1):56-64

［2］李新蕊.主成分分析、因子分析、聚类分析的比较与应用［J］.山东教育学院报，2007(6):1-4

［3］茆诗松，程依明，濮小龙.概率论与数理统计教程［M］.北京:高等教育出版社，2011

［4］杨俊英，杨洋，唐龙妹，等.典型相关分析［J］.临床荟萃，2006，21(1):52-53

［5］华东师范大学.数学分析［M］.北京:高等教育出版社，2010

［6］姜启源，邢文训，谢金星，等.大学数学实验［M］.北京:清华大学出版，2005

Application of Typical Correlation Analysis to the Composition Analysis of Wine Grapes and Wine

TANG Hong-yu，ZHOU Lin，CHEN Yi-an
(School of Mathematics and Statistics，Chongqing Technology and Business University，Chongqing 400067，China)

According to physical and chemical indicators of wine grape and wine，the model is set up based on the idea of dimension reduction step by step and retaining the information to classify original multi-variable to several comprehensive indicators and to study these comprehensive indicators so as to simplify the solving process of the problems.Because the intrinsic connection and changing law between wine grapes and wine quality have randomness and because their physical and chemical indicators are too large，this paper firstly makes variable substitution by selecting 15 comprehensive variables and 8 comprehensive variables respectively to replace original variables，then conducts primary component analysis on wine grapes and wine and finally carries out typical correlation analysis.

dimension reduction;principal component analysis;variable substitution

O211

A

1672-058X(2014)01-0093-05

责任编辑:田 静

2013-05-22;

2013-05-30.

唐洪玉(1990-)，女，四川宜宾人，从事数学金融研究.

＊＊通讯作者:陈义安(1969-)，男，四川渠县人，教授，从事应用数学研究.E-mail:chenyian@ctbu.edu.com.