均匀半空间回线源非中心点频率域电磁场计算

刘 磊，范 涛，李 貅，智庆全

（1．中国煤炭科工集团 西安研究院有限公司，西安 710077；2．长安大学地质工程与测绘学院，西安 710054）

均匀半空间回线源非中心点频率域电磁场计算

刘 磊1，范 涛1，李 貅2，智庆全2

（1．中国煤炭科工集团 西安研究院有限公司，西安 710077；2．长安大学地质工程与测绘学院，西安 710054）

在回线源频率域非中心点磁场计算过程中，会遇到双贝塞尔函数积分问题。这里给出了一种基于静磁场毕奥－萨伐定律计算双贝塞尔函数积分的数值方法，将频率域电磁场写成由回线源直接激发的一次场和由地下导电介质感应出的二次场的和的形式，根据一次场和二次场被积函数的形态区别，对两部分的积分采用不同的计算方法。为了验证该方法的准确性，将回线源剖分成若干个电偶极子，用电偶极子叠加的电磁场与本文提出方法计算的结果对比。对比结果表明，二者的相对误差很小，这有助于研究回线源电磁场的分布规律。

瞬变电磁法 ；双贝塞尔函数 ；毕奥－萨伐定律

0 引言

在回线源频率域电磁场正演模拟研究中，中心点磁场响应特征研究比较详尽，而非中心点电磁场的研究相对较少。相比于中心点计算表达式，非中心点电磁场的表达式更为复杂，是含有双贝塞尔函数的积分形式，该类积分由于强震荡性和积分区间无限大，要求得精确的积分结果十分困难。

对于震荡函数的积分，Filon［1］采用折线逼近的方法，折线逼近的办法在积分区间有限时，计算效果较好，当积分区间无限时，折线逼近方法会遇到很大的困难；Iserles等［2］用构造新的函数表达式的方法对截断点到∞区间的积分进行逼近；陈入云等［3］在Iserles的基础上，给出了一种改进的渐近算法，并根据误差理论给出了数值积分的误差，该算法对于单个贝塞尔函数积分效果较好，但不能完全适用于双重贝塞尔函数的积分；张爽等［4］利用贝塞尔函数展开形式进行积分计算并计算了误差；华军［5］对折线逼近法进行了改进，他将无限的积分区间分为两个积分区间，在有限的积分区间内利用一般的数值积分方法，在截断的无限区间内，使用正余弦变换的方法计算积分；Chave［6］利用连分式的办法解决了有限区间内计算速度和计算精度之间的矛盾，但对于积分区间无限长的情况，效果不佳；薛国强等［7］利用华军给出的计算方法研究了方形回线瞬变电磁的瞬变电磁场响应特征。无论使用何种算法，积分区间都是无限的，要取得精确的计算结果，需要的计算时间都较长。本研究根据回线源频率域电磁场的推导过程，结合一次场对应的物理意义，将无限区间的双贝塞尔函数积分等价成沿发射回线的回路积分，简化了积分计算过程并提高了计算速度。

1 回线源产生的频率域电磁场

均匀半空间情况下大回线频率域垂直磁场表达式为［8］

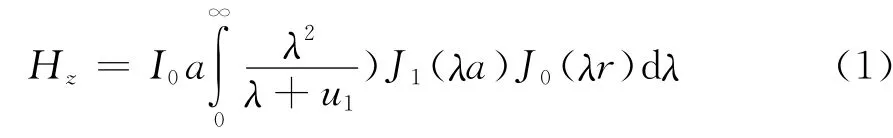
在磁场表达式的积分中，含有0阶和1阶贝塞尔函数，被积函数震荡性很强且积分区间无限，不能直接求取。在频率域，磁场是由激发电流产生的一次场和由导电介质感应产生的二次场共同构成。从标量赫兹位出发，分别对一次场和感应场表达式进行分析，可得计算总场的简便方法。均匀半空间回线源频率域磁场标量赫兹位的表达式为

根据标量赫兹位与磁场的关系

回线源频率域磁场的垂直分量可以写成如下的形式

其中：

式中 ：f1是一次场的表达式，由激发电流直接产生；f2是感应场的表达式，由地下涡旋电流产生；a是发射回线的半径；r是计算点与回线圆心偏离的距离。

要精确计算积分表达式的值，必须了解被积分函数f1、f2的形态，在计算过程中，选取回线半径a的值为100 m，偏移距离r的值为60 m。一次场和二次场核函数形态如图1及图2所示。

一次场核函数是高震荡函数，不能用常规的方法得到积分结果，而二次场核函数在出现极大值之后迅速衰减，用一般的积分方法可以计算得到。

对定义在区间［0，1］上的连续函数积分，可以用函数在某些点的值与其对应的权值的积之和代替积分结果：

ai、xi分别为对应的高斯系数和高斯点，对于积

图1 f1被积函数形态Fig．1 The pattern of integration expression f 1

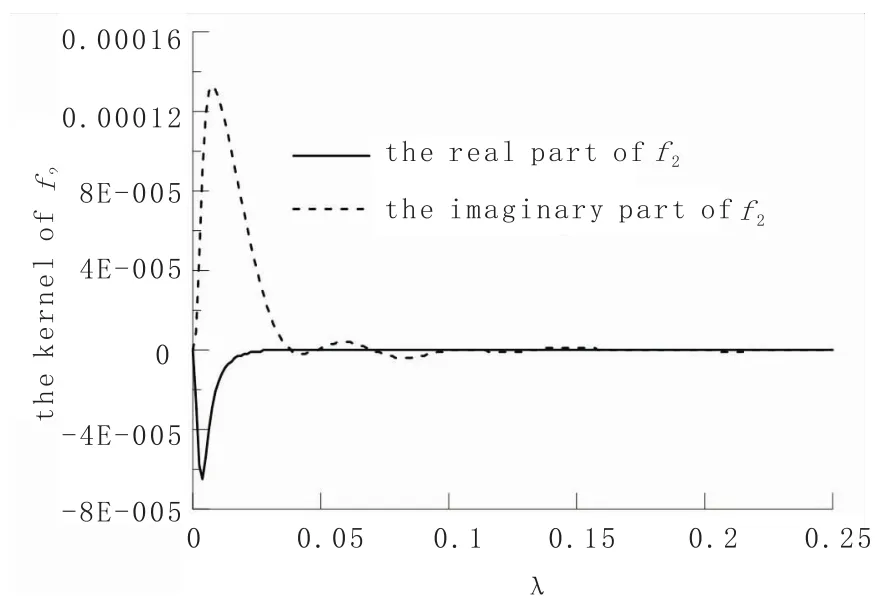
图2 f2被积函数形态Fig．2 The pattern of integration expression f2

分区间在［a，b］上的积分，通过积分变换将积分区间转换到［0，1］区间：

在本文的计算过程中，将二次场积分区间截断，截断区间为［0，1］，将截断区间剖分成若干子区间，在每个子区间内采用七点高斯积分，可以比较精确地得到二次场积分结果。

一次场是由发射电流直接激发，而回线源激发的磁场可通过毕奥－萨伐定律计算，双贝塞尔函数无限区间的积分可以等价地表示成沿线圈的回路积分：

对公式（9）进行进一步化简得到关于一次场的表达式

从表达式（10）可以看出，积分在a＝r（接收点在线圈所在的位置）时奇异，这是由于不考虑发射回线截面积大小时，激发电流密度无限大，该点处的磁场强度无法确定。

关于一次磁场的高震荡无穷积分，根据其对应的物理含义，可以用一个比较简单的定积分公式表示，该积分又可以利用本文所提到的高斯积分公式求取，线圈平面内任意一点的场值都很容易得到，这样大大简化了非中心点磁场计算过程，节省计算量。

2 验证实例

均匀半空间回线源中心点存在解析解，为了验证本文方法的正确性，选取发射回线半径为100 m，半空间电阻率为100Ω·m，选定计算频率范围为10－2Hz～106Hz，中心点处解析解与本文所提出的数值解对比结果如图3及图4所示。

图3 中心点计算结果对比Fig．3 The contrast of result in the center point

从计算的结果看出，将总场分解成由回线产生的一次场由地下介质产生的二次场的计算结果和解析结果相差很小，在频率为10－2Hz～106Hz范围内，解析解和数值解实部、虚部最大相对误差均小于0．4%。

图4 中心点场值计算相对误差Fig．4 The relative error of the result in the center point

当测点位于中心点时，偏移距为0 m，被积函数中只出现一个贝塞尔函数，为进一步验证本文给出的方法在任何偏移距下都成立，需给出一个比较准确的对比结果。采用文献［9］中的方法，将回线源剖分成若干段，任意点电磁场的值等于所有偶极子在该点产生的场值的叠加。任意点磁场可以用式（11）表示。

选取发射回线半径为100 m，偏移距 r＝60 m，半空间电阻率为100Ω·m，两种方法计算得到的非中心点场值及误差对比结果见图5及图6。

图5 非中心点计算结果对比Fig．5 The contrast of result in the non－central point

由非中心点的计算结果表明，当计算频率在10－2Hz～106Hz范围内时，随着频率的增加，基于偶极子叠加计算的结果与本文给出的方法相比，实部和虚部的相对误差都有所增加，相对误差最大值小于4%。

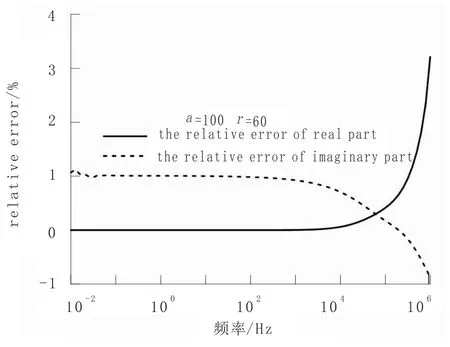
图6 非中心点计算结果实、虚部误差分布Fig．6 Therelative error distribution of the real and imaginary part

由于与激发源的相对位置不同，磁场在回线源不同位置有不同的变化规律，选取回线半径为100 m，半空间电阻率值为100Ω·m，激发频率分别为10－2Hz～106Hz，接收点分别位于0 m、30 m、60 m、90 m、120 m、150 m，利用本文给出的方法，计算了不同位置磁场结果。

图7 不同偏移距场实部与频率关系Fig．7 The relationship of the frequency and the real part of magnetic field at different offset

在发射线圈内部，随着偏移距离的变大，磁场实、虚部随频率的变化规律一致，对于实部，磁场幅值逐渐变大，虚部最大值对应的频率增高（图7）；在线框的外部，磁场的实部与虚部符号均与线圈内相反，这与激发场在线圈位置处方向发生变化相对应（图8）。

3 结论

图8 不同偏移距场值虚部与频率关系Fig．8 The relationship of the frequency and the imaginary part of magnetic field at different offset

1）回线源中心点与非中心点磁场计算结果表明，可以将回线源频率域的场分开写成一次场和二次场的和，根据各自代表的物理含义，频率域磁场关于一次场的无限区间双贝塞尔函数积分，可以等价地写成一种沿发射回线的闭合回路积分形式。这避免了计算震荡积分和积分区间无限大的问题，大大简化计算过程，节省了计算时间。

2）利用毕奥－萨伐定律求得一次场后，二次场利用一般的数值积分方法就可以完成，利用本文给出方法与解析解结果及文献［9］给出的方法对比表明，本文提出的方法是有效的。

3）对非中心点磁场的计算结果表明，非中心点磁场随激发频率的变化与中心点有相似的规律，在发射线圈内，非中心点场值与中心点场值实部表现为幅值的差异，虚部表现为最大值对应的频率发生移动，在发射线圈外部，实部与虚部的符号均与线圈内相反。

［1］ FILON L N G．On a quadrature formula for trigonometric integrals［J］．Proc Royal Soc Edinburgh，1928（49）：38－47．

［2］ ISERLES A，NORSETT S P．On the numerical quadrature methods for highly oscillatory integrals and their implementation［J］．BIT Numerical mathematic，2004（44）：755－772．

［3］ 陈入云，向淑晃．一类含贝塞尔函数积分的数值算法［J］．重庆工学院学报：自然科学版，2008，22（11）：83－88．

［4］ 张爽，郭欣，宋立军．利用贝塞尔函数的级数形式进行数值计算的误差分析［J］．吉林大学学报，2004，14（2）：57－59．

［5］ 华军，蒋延生，汪文秉．双重贝塞尔函数积分的数值计算［J］．煤田地质与勘探，2001，29（3）：58－61．

［6］ ALAN D．Chave，numerical integration of related Hankel transforms by quadrature and continued fraction expansion［J］．Geophysics，1983，48（12）：1671－ 1686．

［7］ 薛国强，李貅，郭文波，等．大回线源瞬变电磁场响应特征［J］．石油地球物理勘探，2007，42（5）：586－590．

［8］ 李貅．瞬变电磁测深的理论与应用［M］．陕西：陕西科学技术出版社，2002．

［9］ 李建平，李桐林，张亚东．层状介质任意形状回线源瞬变电磁场正反演［J］．物探与化探，2012，36（2）：256－258．

A new calculation method for double bessel function integration

LIU Lei1，FAN Tao1，LI Xiu2，ZHI Qin－quan2
（1．Xi'an Research Institute of China Coal Technology＆Engineering Group Corp，Xi'an 710077，China；2．College of Geology Engineering and Geomatics，Chang'an University，Xi'an 710054，China）

According to the double Bessel function integration account in the process of calculation non－center point transient electromagnetic field，a new numerical method based on Biot Savart Law was offered in this paper．We describe the field as the summation of primary field stimulate by the loop and secondary field generated by the media，after analysis the pattern of the kernel function，calculated the two integral function with respective method．In order to confirm the validity，subdivision the loop into some electric dipole，comparing the result acquire by superposition every electric dipole to that gain from the method offered，it prove the effectiveness of the new method．

TEM；double Bessel function；Biot Savart law

P 631．3＋25

A

10．3969／j．issn．1001-1749．2014．05．07

1001-1749（2014）05-0555-05

2014-02-24 改回日期：2014-05-23

“十二五”国家科技重大专项（2011ZX05040-002）；国家自然科学基金项目（41104087）

刘磊（1988－），男，硕士，从事煤田地质勘探方面研究，Ej-mail：chdliulei＠163．com。