Excel在地球化学数据处理中的高级应用

谭亲平，夏 勇，谢卓君，闫 俊

（1．中国科学院地球化学研究所，贵阳 550002；2．中国科学院大学，北京 100049）

Excel在地球化学数据处理中的高级应用

谭亲平1，2，夏 勇1*，谢卓君1，2，闫 俊1，2

（1．中国科学院地球化学研究所，贵阳 550002；2．中国科学院大学，北京 100049）

Excel强大的图表绘制和数据计算能力，为地球化学数据的处理提供了便利。在研究地球化学数据处理原理的基础之上，详细解释了三角图解，频率直方图，概率格纸图解法求异常下限，多重分形法计算异常下限，R型聚类分析和判别分析的具体计算步骤。这些方法有利于地质科技方面的研究。

三角图解；异常下限；直方图；聚类分析；判别分析

0 引言

在地质工作中，常常需要计算各种数据，绘制各种图表［1－3］，目前尚无统一的软件能够满足地质工作当中所有的数据处理的需求。Excel为大众软件，地质科技人员较为熟悉，并有一定的操作经验。它的强大的图表绘制和数据计算能力基本能满足地质工作中的数据处理需求。作者以Microsoft Excel 2010为界面，以文献和作者在工作中的数据为例，详细解释各种地质数据处理的原理和具体操作步骤，它适用于基层地质科技人员的工作性质和工作条件。本研究涉及了Excel的高级用法，需要了解相关的多元统计学知识，并能熟练操作Excel才能合理地进行运用。

1 三角图解

Microsoft Excel已经提供了大量的图表类型，但在地学中需要经常应用的三角图解却没有提供。在Excel中，可以通过将三角坐标转化为直角坐标的办法来“迂回”实现。三角图解有a、b、c三个轴，它们的值范围都是0～100，且满足a＋b＋c＝100。通过坐标变换可将三维坐标系（a、b、c）转换为二维直角坐标系（X，Y），然后再利用转换得来的直角坐标绘制散点图即可实现三角图解的绘制。

图1中直角坐标的原点设为BC的中点，任意点D在三角图解中的坐标设为（a，b，c）。根据几何学原理，任意点D在直角坐标中的坐标是：X＝（b＋c）／2－b，Y＝sin60°*a。设A、B、C三个端点的坐标分别为：A（100，0，0）、B（0，100，0）、C（0，0，100），根据上面的公式计算出它们的直角坐标分别为：A（0，86．60254）、B（－50，0）、C（50，0）。在Excel中利用三个端点的直角坐标，每两个点绘制带直线的散点图，就能得到三角图解的外框。将需要处理的数据，根据同样的公式，也转换成直角坐标，然后添加为散点图即可。

下面通过一个实际的例子来说明三角图解的绘制过程。表1中的原始数据来自文献［4］。以表1中的第2排数据为例，在D2中输入函数：＝100／（A2＋B2＋C2），即可得到比例因子，再将每个变量乘以比例因子，可在E2：G2中得到归一化后的值。归一化后使三个变量之和等于100。在H2和I2中分别输入函数：＝（F2＋G2）／2－F2和＝E2 *√3／2得到相对应的直角坐标，将得到的直角坐标添加到前面已生成的三角形外框中，在生成的图中删除直角坐标轴，插入三个文本框，在文本框中填入三个端元符号。图2是应用本文的方法得到的图，它与文献［4］中的图重合。该方法的关键为三角坐标向直角坐标的转换原理。

表1 三角图解数据表Tab．1 Data table of triangular chart

图1 三角坐标转直角坐标原理图Fig．1 Schematic diagram of traingular coordinate transform into rectangular coordinate

2 频率直方图

频率直方图在Excel中的绘制过程，可利用实例来说明。假如有表2的A列中的一组数据需要绘制频率直方图，首先在B3和B7中分别输入函数：＝MIN（A2：A13）和＝MAX（A2：A13），计算出该组数据的极值。根据极值和实际需要确定分组间隔，本次分组间隔为2。在C2中输入极小值整数位，在C3中输入：＝C2＋2，选中C2：C3，按住鼠标左键将其拖拽至极大值即可得到分组。然后应用“直方图”工具就能绘制频率直方图。首次使用分析工具需加载计算工具：文件－选项－自定义功能区在“开发工具”选项前打勾－确定，然后选择开发工具－加载项－选中“分析工具库”和“规划求解”加载项－确定。工具加载完成后：数据－数据分析－直方图，就能出现频率直方图对话框（图3）。

图2 三角图解应用实例图Fig．2 Application example of triangular chart

表2 频率直方图数据表Tab．2 Data table of frequency histogram

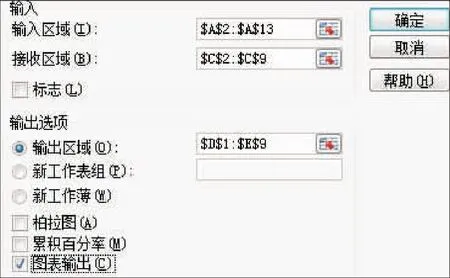
图3 频率直方图对话框Fig．3 Dialog box of frequency histogram

图3中“输入区域”需要输入原始数据：＝A2∶A13，在“接收区域”需要输入分组数据：＝C2∶C9，输出选项中选中“输出区域”，输入任意空白区域，本文实例中输入：＝D1∶E9，选择“图表输出”，最后确定，就能得到D列数据和相对应的频率直方图。如需要将多组数据在一张图中表示，只要将每组数据经过上面的步骤处理，然后在某一频率直方图中添加数据即可：右击－选择数据－添加。该方法的关键是分析工具库中直方图的使用技巧。

3 概率格纸图解法求异常下限

概率格纸图解法确定背景值和异常下限，是建立在元素在地质体中呈正态分布或对数正态分布的基础上。应用这种方法时，统计元素各个分组区间内的累积频率，并在概率格纸上绘出各个累积频率分布点的连线，然后根据其在概率格纸上反映的正态分布（或对数正态分布）特点，确定背景值及异常下限。其在Excel中的具体做法和步骤如下。

图4是在Excel中绘制的概率格纸，其中纵坐标是正态分布累积频率的反函数值（实际标记为累积频率），横坐标是元素含量的对数值（数据已通过正态检验）。表3中A、B、C和D列是绘制概率格纸横向网格的数据，在A和C列中假设一组累积频率，在B和D列中计算各自对应的反函数值，比如在B2中输入函数：＝NORMSINV（A2%）。函数NORMSINV（probability）返回标准正态分布累积函数的反函数值。

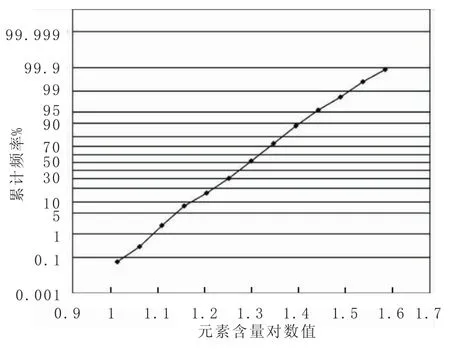
图4 元素含量累积频率分布图Fig．4 Chart of cumulative frequency distribution of element content

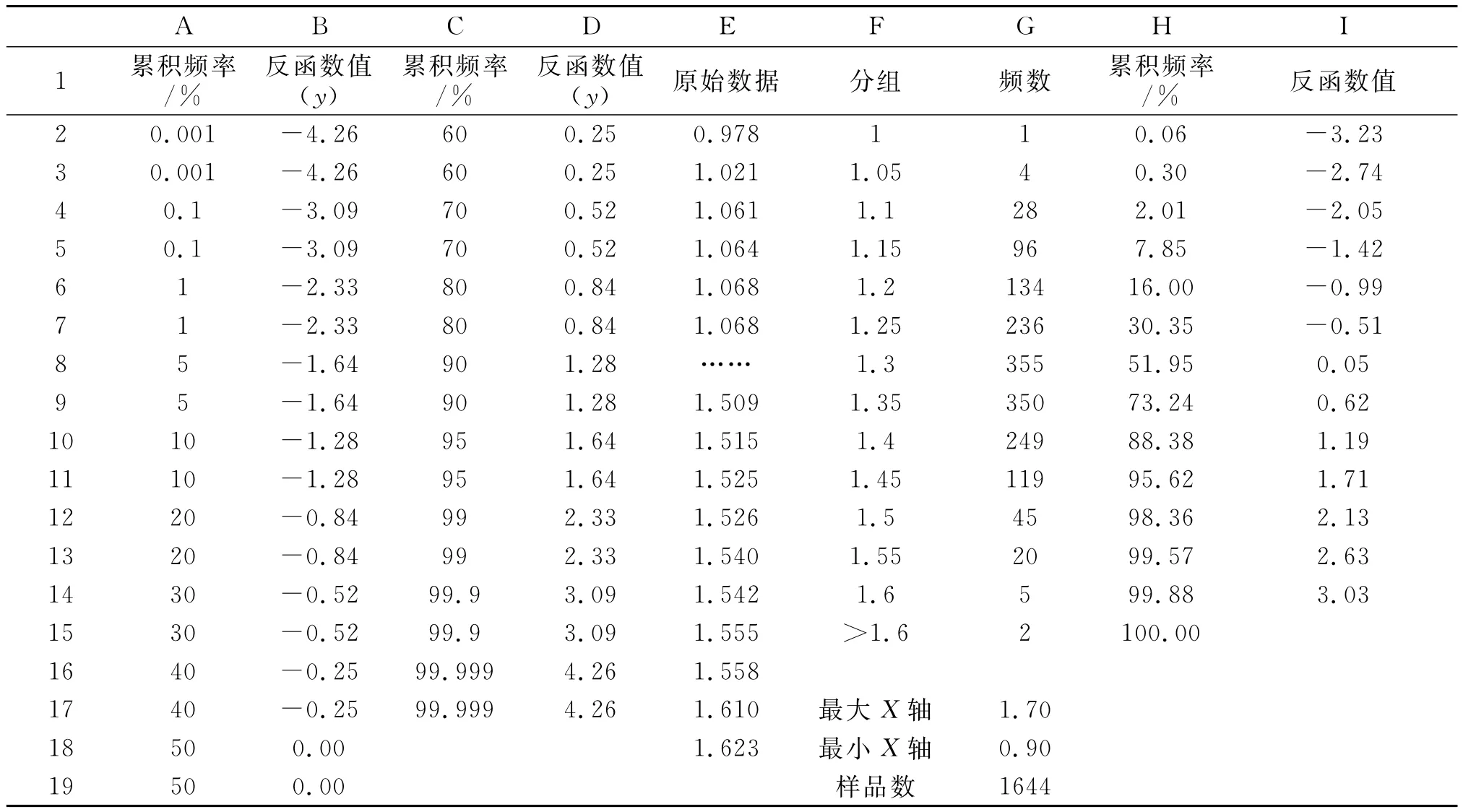
表3 概率格纸法求异常下限数据表Tab．3 Data table of probability ruling paper method to calculate anomaly threshold

以纵坐标为0．1%的横向网格线为例，介绍横向网格的绘制方法。首先绘制带直线的散点图：插入－散点图－带直线和数据标记的散点图－在图中右击－选择数据－添加，出现“编辑数据系列”对话框，在“系列名称”中输入：＝A4（累积频率值0．1%），在“X轴系列值”中输入：＝G17∶G18（图4中X轴的极大值和极小值），在“Y轴系列值”中输入：＝B4∶B5，点击“确定”后出现一条横向直线。选中该直线右击，选“添加数据标签”，在直线端点处出现标签数据，选中该标签数据右击，选择“设置数据标签格式”并出现对话框，在“标签包括”里只选择“系列名称”，在“标签位置”中选择“靠左”，关闭后删除右端点的数据标签即可。其他的网格线利用此方法一一添加，并将X轴的极大值和极小值固定为G17∶G18中的数值，删掉Y轴坐标即可。

概率格纸绘制好之后，将需要计算的数据添加到概率格纸中，就可以计算异常下限和背景值。表3中E、F、G、H、I列中的数据是数据的处理过程，其中分组和频数的计算参考上面频率直方图的方法。H列中累积频率的计算以H2和H3为例分别输入函数：＝G2／1644*100，＝G3／1644*100＋H2。I列中利用函数NORMSINV（probability）返回累积频率的反函数值。所有数据计算好之后，将数据添加到已绘制好的概率格纸中，X轴输入：＝F2∶F14（分组），Y轴输入：＝I2∶I14（实际应为反函数值，但Y轴标记为累积频率），适当调整后就能得到图4。图4中连线与累积频率为50%线的交点的横坐标为背景值，连线上累积频率为97．7%的点横坐标即为异常下限。该方法的关键在于概率格纸的绘制，但绘制好之后可以多次使用，以后只需将新的数据添加在已绘制好的格纸上即可。

4 多重分形法计算异常下限

目前利用分形技术进行地球化学异常下限确定的方法主要有：含量－周长法、含量－面积法、含量－距离法、含量－频数法等。这里采用含量－频数法，设分形求和模型：N（Ci）＝kC－Di（i＞0），式中Ci为元素含量，又称特征尺度，k为比例常数（k＞0），D为一般分维数，N（Ci）为当元素含量为Ci时所有大于等于Ci的元素含量的和数。分形求和模型两边分别取对数得到一元线性回归模型：lg N（Ci）＝－Dlg（Ci）＋lg（k），用最小二乘法求出斜率D的量，即为分维数。Excel中多重分形法的计算过程如下。

表4中对A列中的数据进行分组并计算频数，C列对B列中的分组数据求对数，如在C2中输入：＝LOG10（B2），F列中为当元素含量为Ci时所有大于等于Ci的元素含量的和数，如在F5中输入函数：＝E5＋F6，G列对F列中的数据求对数，如在G2中输入：＝LOG10（F2）。然后绘制散点图：X轴中输入：＝C2∶C15，Y轴中输入：＝G2∶G15，其散点大致分布在两段直线上，同时在图中可确定两段直线的分界点。根据分界点，两段直线在表4中的坐标数据分别为：X＝C2∶C8，Y＝G2：G8和X＝C9：C15，Y＝G9∶G15。确定好两段直线的坐标数据之后，重新绘制散点图，分别输入两段散点的X、Y坐标，生成两段散点，然后分别选中一段散点，右击弹出下拉菜单，选择“添加趋势线”，弹出“设置趋势线格式”对话框，在“趋势线选项／回归分析类型”中选择“线性”，同时在“显示公式”前的方框中打勾，最后关闭即可。该方法的关键在于理解多重分形法的原理。

表4 多重分形法数据表Tab．4 Data table of multifractal method

图5 元素含量－频数双对数曲线Fig．5 Chart of element content frequency double logarithmic curve

5 R型聚类分析

R型聚类分析是根据样品的多种变量的测定数据进行数字分类，定量地确定变量之间的亲疏程度［5］。进行数字分类，需要选择合适的数量指标，以此衡量样品之间的亲疏程度。数量指标主要有距离系数，相似系数和相关系数。本研究用相关系数作相似性统计量的逐步计算形成法做R型聚类分析，将通过一个实际例子，说明在Excel中聚类分析的计算步骤。

由于各变量的单位，量级和数值变动范围的差异很大，计算中往往突出了那些绝对值较高的变量。因此，在进行聚类分析之前需将各个变量换算成一致的相对值。常用的变换的方法有标准化和正规化，本例中选择标准化。例如表5中B2∶G7为原始数据，在第8和第9行中分别计算均值和标准差，比如分别在B8、B9中输入函数：＝AVERAGE（B2：B7）和＝STDEV（B2：B7），然后选中拖动即可全部算出。在B11∶G16中计算出标准化数据，比如在B11中输入函数：＝（B2－B8）／B9。标准化之后的数据，均值为0，标准差为1。数据标准化之后即可计算相关矩阵：数据－数据分析－选中“相关系数”－确定，然后弹出“相关系数”对话框（图6），在“输入区域”选中B10∶G16，在“分组方式”中选择逐列，选中“标志位于第一行”，在“输出区域”中选择A19，确定之后会得到表5中A9∶G25的相关矩阵。从相关矩阵中可以看出Cu和Co相关系数最大，因此首先将Cu和Co连为一组。逐步加权平均，即新的CuCo＝（Cu＋Co）／2，计算修正数据，将得到的新数据CuCo替换Cu和Co，并与其他数据一起，计算新的相关矩阵，直到所有元素均已分组完成（表6）。最后在绘图软件中根据上面的计算结果，绘制出谱系图即可（图7）。

表5 聚类分析数据表Tab．5 Data table of R cluster analysis

表6 R型聚类分析连结顺序表Tab．6 Link sequence table of R cluster analysis

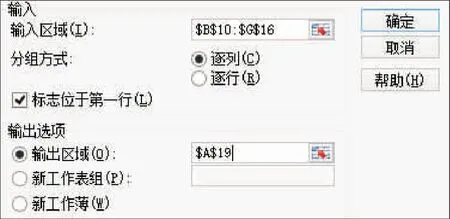
图6 相关矩阵对话框Fig．6 Dialog box of correlation matrix

6 判别分析

若有两个母体，按照某种准则，把它们的P种特征（变量）组合成一个综合指标（关系式），称为判别函数，使两类母体的区分率达到最好［6］。判别函数中最简单的形式是线性函数。有p个变量n个样品的两个母体的判别函数可以写成：

代表每个变量的方差和，当k≠f时Skf代表两两变量之间的协方差和。方差／协方差的定义为同一／不同变量之间的偏差乘积的平均数。但是根据Skf表达式，Skf应为方差或协方差的n倍（n为样品数）的和。实际胡以铿［7］在《地球化学中的多元分析》中的计算实例中Sif也是方差或协方差的n倍的和。

图7 R型聚类分析谱系图Fig．7 Pedigree chart of R cluster analysis

作者以文献［7］中的实例来说明在Excel中判别分析的计算过程。表7中第3到第9行为原始数据，共7个样品（n＝7），在第10行计算每个变量的均值，比如在B10中输入：＝AVERAGE（B3：B9），在第11行中计算两组样品同一变量的均值差，比如在B11中输入：＝B10－E10，在第12行中计算每个变量方差的7倍，比如在B12中输入：＝VAR．P（B3：B9）*7，在第13行中计算两组样品中同一变量方差的加和，比如在B13中输入：＝B12＋E12，其中B13，C13，D13分别代表S11、S22、S33，同理在B14、B15中分别计算协方差的7倍以及协方差和，分别输入：＝COVARIANCE．P（B3：B9，C3：C9）*7和＝B14＋E14，其中B15、C15、D15分别代表S12、S13、S23。经过上面方差和协方差的计算得到如下方程组：

将方程组的系数在第16、17、18行中按顺序排列，在E16、E17、E18中分别输入函数：＝B16*B19＋C16*C19＋D16*D19，＝B17*B19＋C17*C19＋D17*D19，＝B18*B19＋C18*C19＋D18* D19，此时E16、E17、E18中的值均显示为零。然后利用“规划求解”解线性方程组：数据－规划求解－弹出“规划求解参数”对话框（图8），在“设置目标”中输入：＝E16，在目标值中输入：0．5571，在“更改可变单元格”中输入：＝B19∶D19，在“遵守约束”中点击“添加”，在弹出对话框中分别输入：E17＝F17，E 18＝F18，最后把“使无约束变量为非负数”前的“勾号”去掉，确定即可得到B19∶D19中的三个解，同时E16、E17、E18中的值也变为非零。获得方程组的解之后，就可以列出判别函数，判别显著性检验以及对未知样品的判别，本文略。本文计算结果与文献［7］中实例计算中的微有差别，这是在计算过程中保留有效数字个数不同造成的（本文计算过程中保留9位有效数字，实际在表7中显示4位）。该方法的难点为判别分析的原理，方差／协方差的计算以及利用“规划求解”解方程组技巧。

图8 规划求解对话框Fig．8 Dialog box of solution of programming

7 结论

Excel为大众软件，除本研究中提到的应用外，微量／稀土配分图，散点图，相关性计算，正态检验，样品化验数据误差的检验，一次趋势面分析等等都可以用Excel来实现。因此熟练使用Excel基本能满足地球化学的数据处理需求。地球化学数据处理多种多样，有时需借助好几种软件甚至收费的软件才能实现各种计算需求，每一种软件又需要花费一定的时间去掌握和熟练。熟练使用Excel不失为较为理想地选择，对地质人员较为适用。

表7 判别分析数据表Tab．7 Data table of discriminant analysis

参考文献：

［1］ 蒋敬业，程建萍，祁士华，等．应用地球化学［M］．武汉：中国地质大学出版社，2006．

［2］ H．E．霍克斯，J．S．韦布．矿产勘查的地球化学［M］．谢学锦，译，廊坊：地质科学院物探研究所，1974．

［3］ 伍宗华，古平．隐伏矿床的地球化学勘查［M］．北京：地质出版社，2000．

［4］ 李明欣，梁斌，王全伟，等．川西龙泉山白垩系泥质岩的元素地球化学特征［J］．高校地质学报，2013，19（2）：346－354．

［5］ 春乃芽．利用Excel实现R型聚类分析［J］．物探与化探，2007，31（4）：374－376．

［6］ 春乃芽．利用Excel实现判别分析［J］．物探化探计算技术，2007，29（6）：560－564．

［7］ 胡以铿．地球化学中的多元分析［M］．武汉：武汉地质学院地球化学教研室，1984．

［8］ 罗先熔，文美兰，欧阳菲，等．勘查地球化学［M］．北京：冶金工业出版社，2007．

Advanced application of Excel in geochemical data processing

TAN Qin-ping1，2，XIA Yong1*，XIE Zhuo-jun1，2，YAN Jun1，2
（1．State Key Laboratory of Ore Deposit Geochemistry，Institute of Geochemistry，Chinese Academy of Sciences，Guiyang 550002，China；2．University of Chinese Academy of Sciences，Beijing 100049，China）

The Excel functions of chart drawing and data computing facilitate geochemical data processing．With studying in the principle of geochemical data processing this paper explains the calculation steps of the triangular diagram，the frequency histogram，the probability ruling paper graphical method for anomaly threshold，the multifractal method to calculate anomaly threshold，R cluster analysis，and discriminant analysis．These methods are entirely applicable to geochemical data processes．

triangular diagram；anomaly threshold；histogram；cluster analysis；discriminant analysis

P 632

A

10．3969／j．issn．1001-1749．2014．05．21

1001-1749（2014）05-0626-08

2014-03-07 改回日期：2014-08-19

国家重点基础研究发展计划（973计划）（2014CB440905）；矿床地球化学国家重点实验室＂十二五＂项目群课题（SKLODG－ZY125－01）

谭亲平（1986-），男，博士，从事构造地球化学研究，E-mail：565310821＠qq．com

*通讯作者：夏勇（1960-），男，博士生导师，从事矿床地球化学研究，E-mail：xiayong＠vip．gyig．ac．cn