磁电弹性圆环板屈曲问题的哈密顿体系方法

高慧霞，何文明

(温州大学数学与信息科学学院，浙江温州 325035)

磁电弹性圆环板屈曲问题的哈密顿体系方法

高慧霞，何文明

(温州大学数学与信息科学学院，浙江温州 325035)

运用哈密顿体系方法给出了磁电弹性圆环板屈曲问题的解析解，并对磁电弹性圆环板的纯弯曲问题进行了分析．算例结果表明，采用哈密顿体系方法求解磁电弹性圆环板屈曲问题非常方便快捷．关键词：磁电弹性圆环板；哈密顿体系方法；本征解

磁电弹性耦合材料是压磁材料和压电材料的复合体，是一种智能材料，它具有同时感知磁、电、力影响的能力，并且可以实现它们之间的相互转化，即磁场或电场会导致其变形，而材料变形时也可以产生电场和磁场，这种独特的机电和磁力转换能力使得这种材料在工程中的应用十分广泛．

文献[1]采用调和函数的一些函数作线性组合，给出了磁电弹性圆环板的纯弯曲问题的解析解，文献[2]由控制方程出发，采用凑合法给出了磁电弹性旋转圆环的解析解，文献[3]采用微分求积法和状态空间法相结合的半解析数值方法对以上问题进行了求解，这些文献所采用的方法都属于凑合法，具有一定的局限性：求解过程中，由于是一类变量的求解，所以不可避免地会有高阶偏微分方程出现；假设的使用只适应于一些简单的机械模型，对于复杂局面很难给出合理的假设；所得的解是不完整的，只能近似地满足边界条件．

哈密顿体系方法不同于一类变量的求解——拉格朗日体系的解法，它是将原变量和对偶变量组成的状态空间引入到弹性力学，然后再利用分离变量法，导出横方向的本征问题，通过对各阶重本征值解的约当型形式的分析进行求解，通过理性推导，逐步进行下去．哈密顿体系方法已应用到很多问题的研究中，文献[4]给出了哈密顿体系下机电耦合问题的基本方程，文献[5]、文献[6]、文献[7]分别讲述了哈密顿体系方法在弹性圆板热屈曲问题、粘弹性悬臂梁弯曲变形问题及功能梯度压电板 / 管静动力分析中的应用，但关于哈密顿体系方法在磁电弹性圆环板中的应用，目前还未见到相关文献报道．本文将在磁电弹性圆环板屈曲问题中引入文献[8]中的哈密顿体系方法，通过理性推导给出磁电弹性圆环板屈曲问题的解析解．

1 磁电弹性圆环板屈曲问题的基本方程

磁电材料极化后为横观各向同性材料，设极化方向为z轴方向，考虑磁电圆环板内半径为r0，外半径为r1，厚为h，选取柱坐标(r,θ,z)，z轴沿板的厚度方向，坐标原点为板心，可得磁电弹性圆环板的轴对称问题的基本方程，也就是磁电材料的本构方程、几何方程和平衡方程．

本构方程为：

其中，σr、σθ、σz、τzr为应力，εr、εθ、εz、γzr为应变，c11、c12、c13、c33、c44为弹性系数，e31、e33、e15为压电系数，d31、d33、d15为压磁系数，λ11、λ33为介电系数，μ11、μ33为磁性系数，g11、g33为磁电系数，ur、uz为位移，Er、Ez为电场强度，Hr、Hz为磁场强度，φ为电势，ψ为磁势，Dr、Dz为电位移，Br、Bz为磁感应强度．

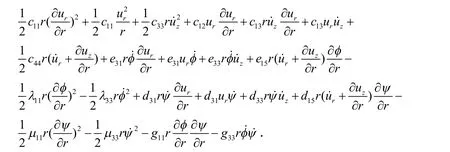
势能可由如下积分表示，记作Π．

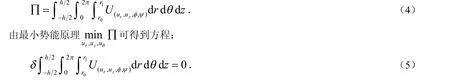
2 导入哈密顿系统

3 问题的零本征解

对方程（6）式采用分离变量法来求解，就可得到磁电弹性圆环板屈曲问题的解，即得到ur,．下面进行变量分离．令

因为有自由边界的存在，原问题必然会存在零本征解，H的零本征值λ=0是很重要的，此时一定产生重根，并且会出现不同阶数的约当型．本文将讨论零本征解，下文会具体地将这些解找出来并赋予其物理意义．现在来寻求这些零本征解，即当λ=0时，方程为：

这组解的物理意义分别为：均匀力拉伸、均匀电场和均匀磁场．

下一步还应寻找更下一阶的约当型．二阶约当型的控制方程为：=，(i=1,2,3)，因为此方程的解不满足问题的边界条件，所以求解过程到此结束．以上的求解已表明，零本征解已全部找到，不会再有别的了，因此该约当型链到此中断，即不存在更高阶的约当型解．

4 哈密顿体系方法的应用

下面将以文献[1]中具体的例子为例，来介绍哈密顿体系方法对该问题的求解过程．

文献[1]中给出的纯弯曲问题的边界条件为：

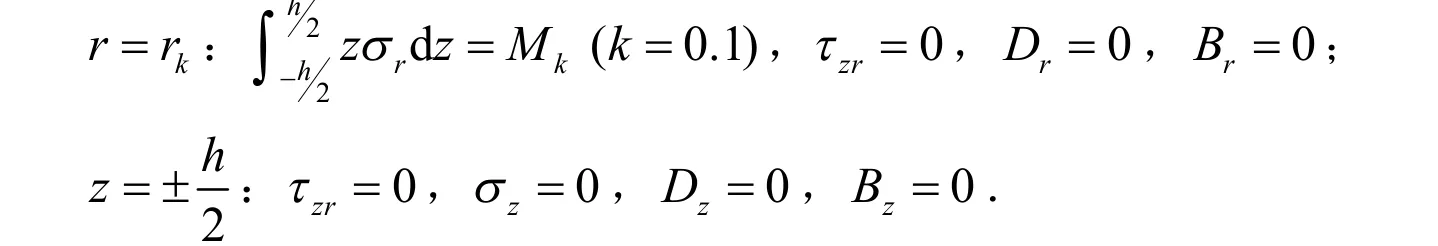
对应的应力场分布结果为：

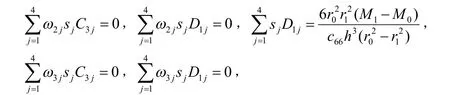
然后再代入到ur、uz、φ、ψ中才可以得到位移、电势和磁势的显示表达式．

本文方法的求解过程如下.

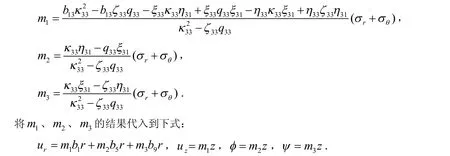
通过对比可以发现哈密顿体系方法更为方便．

[1] 陈江瑛, 侯鹏飞, 丁皓江. 磁电弹性圆环板的三个解析解[J]. 宁波大学学报, 2002, 15(4): 18-21.

[2] 陈江瑛, 丁皓江, 侯鹏飞. 磁电弹性旋转圆环(圆盘)的三维分析[J]. 浙江大学学报, 2003, 37(4): 440-444.

[3] 聂国隽, 仲政. 功能梯度磁电弹性圆板的三维动力特性分析[J]. 同济大学学报, 2009, 37(6): 749-754.

[4] 边文凤, 孙芳, 王彪. 哈密顿体系下机电耦合问题的基本方程[J]. 计算力学学报, 2005, 22(4): 411-414.

[5] 徐新生, 邱文彪, 周震寰, 等. 哈密顿体系下的弹性圆板热屈曲问题[J]. 大连理工大学学报, 2008, 48(1): 1-5.

[6] 张维祥, 邵兴, 徐新生, 等. 粘弹性悬臂梁弯曲变形的哈密顿体系方法[J]. 兰州理工大学学报, 2009, 35(3): 127-130.

[7] 代海涛, 程伟, 李明志. 哈密顿体系下功能梯度电板/管静动力三维解[J]. 北京航空航天大学学报, 2008, 34(1): 104-107.

[8] 钟万勰. 弹性力学求解新体系[M]. 大连: 大连理工大学出版社, 1995: 102-116.

Hamiltonian System Approach to the Bending Problem of Magnetoelectricity Elastic Annular Plate

GAO Huixia, HE Wenming
(School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

The Hamiltonian system approach is used to propose an analytical solution to the blending problem of magnetoelectricity elastic annular plate, and the pure bending problem of the magnetoelectricity elastic annular plate is analyzed as well. Numerical results show that the Hamiltonian system approach to the problem is very convenient.

Magnetoelectric Elastic Annular Plate; Hamiltonian System Approach; Eigensolution

O24

A

1674-3563(2014)04-0017-08

10.3875/j.issn.1674-3563.2014.04.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2013-09-28

高慧霞(1969- )，女，河南濮阳人，硕士研究生，研究方向：计算机数学与复杂系统控制