造假行为的传播与遏制——基于进化博弈模拟的研究

吴怡萍 蔡恒进

造假行为的传播与遏制
——基于进化博弈模拟的研究

吴怡萍 蔡恒进

借鉴进化博弈的思想,一个新的模型建立起来用以模拟造假行为的传播过程,以期找到其广泛传播的路径,并寻找遏制的方法。模型赋予了个体学习的能力,结果显示惩罚程度对造假行为的传播没有影响,但抽查概率却是决定性的。为了提高查处的效率,“连带检查”机制被加入到模型中,即对造假者周围邻居进行检查并施以同样的惩罚。这种机制能够在抽取概率为26%时达到消除造假者的目的,相比之下,没有“连带检查”时必须把抽取概率提高到80%才能达到消除造假者的目的。

进化博弈;造假行为;惩罚机制;连带检查

在漫长的管理进化史中,对“人”的界定是在不断发生变化的。自Adam Smith开始,经济社会中的“人”被认为是“经济人”,即以完全追求物质利益为目的而进行经济活动的主体(雷恩·贝德安,2012:164-169)。建立在自利原则上的“经济人”,拥有完全理性,希望以尽可能少的付出,获得最大化的收获,并可以为此不择手段。之后Herbert Simon指出了完全理性决策只是一种理想模式,因为人们面对的是一个复杂的、不确定的世界,无法获得完全的信息,同时人的计算能力和认知能力也是有限的,其所作的决策不可能不受到外界环境或是情绪的影响,因此无法做到完全理性,而应该是“有限理性”(Herbert Simon, 1997:35-37)。从最初的“机器的操作者”到“拥有智力和感情的机器”,从“完全理性人”到“有限理性人”。管理者对“人”的研究越来越多,管理学的重点也从如何管理机器、生产线以及生产的流程,转变为如何管理人(Harold Koontz,1980:175-187)。

现实市场总是处于不完备的状态,因此交易者的机会主义行为会经常发生。当现有工商市场中制度存在缺陷时,交易主体发现选择机会主义的失信行为有利可图,一旦这种损人利己行为得不到现有制度的惩罚或惩罚不够,就会发生劣币驱逐良币的效果,引发更多人不讲信用,从而使道德进一步滑坡。我们希望借鉴进化博弈的思想来对造假行为的泛滥进行定量分析,用计算机模拟来研究其传播途径,并找到有效遏制方法。

前人在对这些行为进行研究的时候,往往都是从人的心理、制度的不健全或者管理缺失的角度来进行分析(王林燕,2010:214-215)。他们关注的都是造假者与监管机构之间的博弈,这固然可以为监管部门提供一定的参考(刘伟兵、王先甲,2009:28-33)(王先甲、刘伟兵,2011:679-686),但是由于造假者都被看作为一个整体,他们的心理以及造假者行为对相互的影响则被忽视了。我们的模型研究的就是造假者之间的博弈,这是造假行为传播的重要影响因素。

一、模型的理论基础

(一)进化博弈理论

进化博弈最早应用于生物领域,因其另辟蹊径的思维模式而给生物进化指出了一条新的道路,也使得它的影响力逐渐扩大,衍生到各个行业中(Trivers R L,1971:35-57)。其中,进化博弈思想与社会科学,尤其是经济与管理领域的合作,成为跨学科交叉成功的典范。这种将生态学与经济学结合的创新的分析方法,结合了经典博弈理论和社会学理论,将有限理性的人作为观察对象,利用动态分析方法,把影响人行为的各种因素纳入模型之中,来考察群体行为的演化趋势。

进化博弈思想中比较重要的一条就是互惠理论,其实质就是以牺牲目前的利益为代价,换取以后长期的利益(Axelrod R,1984:25-28)。这也是生物学中对于物种间合作的解释,它同样可以被延伸到人的合作中来。前人已经对这种行为进行了深入研究,并通过数学和计算机工具为合作进化过程建模。20世纪80年代,Robert Axelrod完成的计算机锦标赛被认为是最早利用计算机模型完成的合作进化研究。在这个锦标赛中,Tit-for-Tat策略表现得格外优异,成为互惠利他主义的范例(Nowak M A,Sigmund K, 1992:250-253)。这是一种针锋相对的策略,即完全跟随对方的策略,上回合对方合作即合作,上回合对方背叛即背叛。这种策略比较友善,因为初始采取的是合作的策略,而且不会主动背叛对方,但是当遭到背叛的时候也会以牙还牙地进行报复,而当对方停止背叛的时候会立即原来并继续合作。然而这个策略的容错性很差,突变对于系统的影响很大,因此Martin Nowak和Karl Sigmund提出了Generous Tit-for-Tat策略,之后又提出了Pavlov策略(Nowak M A,Sigmund K,1993:56-58),这种策略的基本行为机制是win stay,lose shift(Parkhe,Rosenthal,Chandran,1993:531-539)(Martin Nowak,2006:1560-1563),并通过引入多种概率性策略的不均匀集合,以及突变和选择到进化模拟中来证明Pavlov策略的优越性。Martin Nowak和Karl Sigmund证明了在自然环境下,合作行为可能会经常建立在win stay,lose shift的基础上。

(二)自我肯定需求理论

关于假冒伪劣的博弈模拟,前人大多关注的是造假者与监管机构之间的博弈。而我们认为,造假者之间也存在博弈。造假行为的模仿、造假行为在生产者之间的传播,都是研究造假行为发生所需要关注的部分。因此,我们首先将模型中的个体设定为生产者。

生物领域用合作进化的思想来解释不同物种(Christian Hilbe,Martin A.Nowak,2012:1067),或者不同个体之间的合作现象(Grilo C,Correia L,2011:109-122)。我们在探寻造假行为发生原因的过程中,发现也可以用合作-背叛的模式来进行研究。每个诚信的个体,在面对周围的造假行为时,是会选择坚守诚信,还是同流合污?他们进行选择的依据是什么?我们认为,人的需求来自于理性与自我肯定。我们依据人的参照依赖心理特征,排除掉随机的和完全非理性的需求之后,将需求分为两类——理性经济需求和自我肯定需求(H.J.Cai,2012:1-6)。理性经济需求是每个人在其已掌握信息的基础上做出理性选择后产生的需求。与之相对的是自我肯定需求,它是人在理性经济需求之外的,建立在对自己的主观判断上的需求。我们认为,自我肯定需求源于比较,而这种比较一般有两种:一种是将自己的现在与过去比,另一种是将自己与他人比(H.J.Cai,2011:445-449)。这两种比较加上人对自己的肯定而产生了一种不同于理性经济需求的自我肯定需求。因为人是倾向于肯定自我的,在面对选择时,人更倾向于做出有利于自己的判断,更倾向于认可自己,并期望获得高出平均水平或超出过去水平的报酬或认可。

将这种比较带到博弈中,就是学习和模仿。个体不是孤立存在的,周围个体的行为会对其产生影响。当其中一个个体选择造假,例如用质量较差的原材料替换原有的材料,就能够获得较高的额外收益。排除掉法律和道德的因素,周围的个体会学习并模仿,而使得这一行为逐渐向外传导,影响的范围逐渐扩大。不过当这一行为逐渐传播开来,成为系统中大部分个体的选择的时候,额外的收益逐渐减少直至不复存在。

二、模型的设计

(一)对经典Pavlov模型的改进

Röhl et al.(2011)引入声誉机制,应用进化博弈模型来研究合作中的欺骗行为.他们在模型中构建了三类人——辨别者、背叛者以及欺骗者,每种人再分为声誉好的和声誉差的两种,通过模拟他们两两交互的重复博弈,证明了欺骗者的存在对系统产生有害作用,因为对声誉造假可以促进基于间接互惠的合作行为(Torsten Röhl,Claudia Röhl,2007)。

我们还原了Pavlov策略,用计算机模拟实现了Pavlov策略的多人多次博弈,结果发现这是一种引导合作的策略,不论初始背叛者的比例有多少,最终模型都以全部变为合作者达到稳定状态。显然这种策略的模拟结果与现实情况不符,所以我们对其进行了改进:

Pavlov策略以及之前的各种进化博弈策略使用的都是一对一的交易模式(W.H.Press,F.D.Dyson, 2012:109)(A.J.Stewart,J.B.Plotkin,2012:10134-10135),而我们的模型中对此做了修改,在交互时依然是一

对一,但是决策选择的时候会受到周围个体的影响。人是社会性的动物,其所作的决策会受到周围个体、环境的影响。因此我们的假设为,个体能够获得周围个体的信息,但是并不能获得整个市场的完全信息,而且个体在做决策的时候,会更多地参照自己周围的个体。因此个体在做决策的时候,会将自己的收益与邻居的收益进行比较,以此来选择之后的决策。这样每次交互中,每个个体所关注的信息是它周围这个小的群体中所有个体的信息,并且会对这些信息进行分析和判断,以此来决定自己下一周期的选择。每一周期它会观察自己周围个体的决策和收益,然后学习其中获得收益最高的人。现实生活中的信息和选择,也是依靠这样的方式,通过周期的演进而不断传递出去的。这种心理正是来源于个体的自我肯定需求。其核心观点就是个体的比较,即个体的满足感取决于与周围个体的比较。如果自身获得的收益更高,就能获得更高的满足感;否则即便绝对值很高,也不会获得满足。

在Röhl的模型中,个体决策的改变是通过一系列参数和方程计算出来的,包括被抽到的概率、每一周期付出的成本、可能获得的收益、如果欺骗可能被发现的概率等等,然而我们认为真实的决策没有这么复杂,个体想要改变策略只是因为他看到了更好的策略,而这种认知是通过学习和模仿得来的。基于我们对Pavlov策略的改动,个体认知的范围扩大,其接触的个体有多个,而且他做决策的时候会对这些个体的收益进行综合比较,这就使得较好的决策能够脱颖而出,而周围的个体会对这个决策进行学习。好的决策通过这个过程,可以迅速地在系统中传播出去。当然,不好的但是收益高的决策也是一样,例如造假行为就是一个典型的例子。

(二)具有学习能力的进化博弈模型

我们的模拟是分两步完成的,为了更清晰地探寻造假行为的传播过程,我们首先在模型中不加入惩罚机制,只观察造假行为是如何通过学习和模仿在周围的个体中传播开来的。第二步,再在这个模型的基础之上,加入惩罚机制,并与第一步的结果进行对比,以此来观察惩罚机制是如何发挥作用的。

基于前面提到的修改,我们将这个新的模型建立在一个二维平面中,设定每个个体的认知范围是一个3×3的方格,即他能够获取周围8个个体的所有信息,并且对这8个个体采取的决策是一致的。具体到每次交互,个体的选择只有不造假或造假。双方都不造假时,收益为3;都造假时,收益为1;一方造假另一方不造假时,造假者收益为5而不造假者收益为0。决定其下一周期决策的因素不再是其自身单次收益的高低,而是综合比较周围8个个体的总收益,找出其中收益最高的个体,选择它的决策,作为自己下一周期的决策。

具体到模型中,在V*V的二维平面中存在V2个个体,每个个体i与其周围的每个邻居j进行交互。在i与j的交互过程中,i的收益取决于i和j单次博弈的结果。每个个体每一周期对周围8个邻居的决策是相同的。周期开始时,个体i对周围8个邻居的决策参照上一个周期中自己和8个邻居中获得最多收益的人j,如果j是因为对邻居造假获得的收益,那么i在这一个周期中对所有邻居采取造假决策,反之,i对所有邻居采取不造假决策。

模型的基本还是囚徒困境。每个Agent有不造假和造假两种选择,如果他们都选择不造假,则都获得3的收益;若都选择造假,则都获得1的收益;若一人不造假一人造假,则不造假方获得0的收益而造假方获得5的收益。而Agent每周期的决策,则是采取上一个周期周围获得最多收益者的选择。具体流程如图1所示:

个体i在周期t对周围8个邻居采取统一的决策为Si,t,在这个周期获得的总收益为Pi,t。除了第一个周期,每个个体的决策是随机选取以外,以后的每个周期t(t＞=2),i采取上一个周期中自己和8

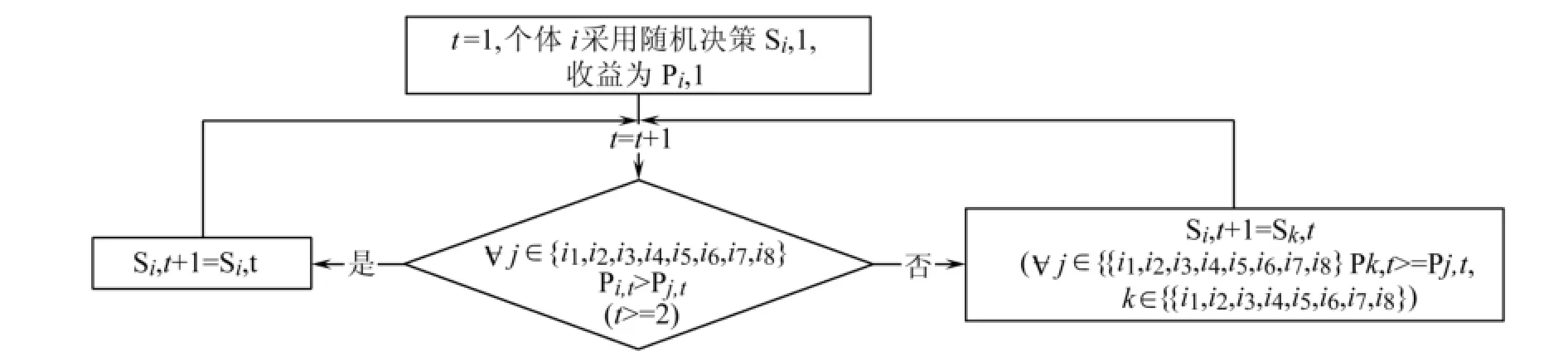
图1 具有学习能力的进化博弈算法流程图

个邻居里获得收益最大的个体j所采取的决策,即个体j在t周期的决策:

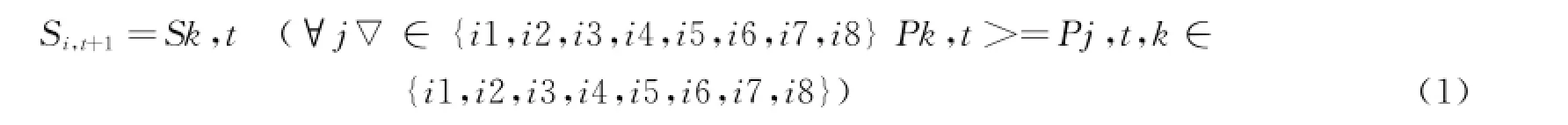
其中i1,i2,…i8分别表示i的8个邻居。当个体i和8个邻居中获得最大收益的人不止一个时,如果获得最大收益的人中有采取不造假决策的,那么i这个周期选择不造假决策;否则i采取造假决策。

三、模型的结果

(一)不加惩罚机制的模拟结果

在前文模型的基础上,我们取V=100来进行模拟实验。当初始状态下所有的个体都不造假的时候,模型不会有任何改变,最后还是都不造假。当加入一定数量的造假者之后,造假的行为开始以不同的程度在整个系统中传播出去。在这个拥有10000个个体的系统中,设定初始造假者比例为0.2%,即初始有约20个个体造假时,随着周期的演进造假行为逐渐扩散并形成网络。从导出的造假者数量可以看出,到大约50周期时,虽然有个别的变化,但是整体来看已经趋于稳定。而这时的整个系统中,可以看出造假者依然占少数,如图2中(4)所显示的,其中蓝色代表的是不造假者,而绿色是造假者。这时蓝色的占主导,而绿色则只是在其中割裂出一些细小的网络。

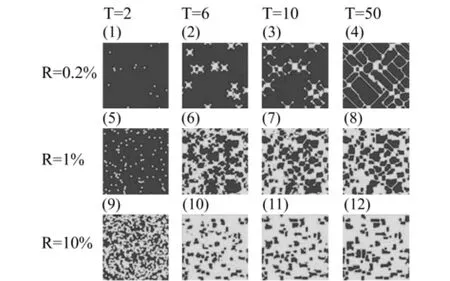
图2 初始造假者比例为0.2%、1%及10%时的个体行为演化图

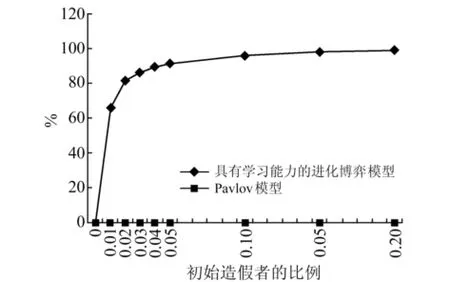
图3 两种模型不同初始造假比例下的最终造假者比例对比图

但是当我们提高这个初始比例的时候,造假者的数量开始急剧增加。当初始造假者的比例为1%时,虽然这个比例很小,但是造假行为的传播却很快。从图(5)到图(6),即从第2周期到第6周期,造假行为迅速扩散,一半的个体开始学习这一行为。因为在大部分人不造假的情况下,少量的造假行为能够带来最高的收益,这样通过模仿传导出去,使得不造假者纷纷转而选择造假。系统在第50周期的时候基本达到稳定状态,如图(8)所示,与图(4)相比,绿色超越了蓝色,数量更多;而当初始造假者的比例为10%时,最终造假的人数更多,如(12)所示,不造假者只能以一个个孤岛的形式存在。

接下来我们对不同初始造假比例下,最终剩余的不造假者进行了统计,并且将其与Pavlov策略的结果进行对比。如下图所示,Pavlov策略下,初始比例从0到20%,最终的不造假者都是100%。而我们建立的新模型则与之完全不同,当初始造假者的比例为1%时,模型稳定后不造假者只剩下33.77%,减少了三分之二;而当初始比例上升为2%时,最终不造假者剩下18.22%,又减少了一半左右;这个比例在初始造假者上升为5%时就已经很低了,为8.69%;直到初始造假者为20%时,基本上所有人转化为造假者。

与Pavlov策略相比,我们模型中的个体能够获得更多人的信息(其周围8个个体的信息),这比Pavlov中每个个体只关注自己的交易对象更为合理;而且,在这个认知范围扩大的进化博弈模型中,个体还能够对自己获得的信息进行比较和分析,将自己周围8个个体的策略和收益进行对比,从中选择收益最高的个人进行模仿,这也使得好的策略能够在系统中传播出去。当然,在这个模型中,不好的行为,例如能够获得短暂高额收益的造假行为,也能够迅速扩散。但是,正是这样的模拟,才更符合实际情况。

由这些数据我们可以看出,在一个不造假者的群体中,只要出现造假者,即使数量很少,也会立即带来巨大的影响,即引导大家走向造假。因为在不造假的环境中,最初的造假能够获得巨大的收益,这就使得其周围的人对其进行学习。但是当造假者大量增加的时候,造假所带来的收益也迅速减少。当系统中全部为不造假者时,即初始造假者比例为0时,所有个体一个周期的收益总和为2.4×105;而当这一比例为0.01时,总收益也降低为1.31×105。随着初始造假者比例的上升,系统中的总收益在逐步降低,直到所有人变成造假者,这时的总收益是最低的。

(二)加入惩罚机制的模拟结果

我们在前面的模型中加入惩罚机制。在每个周期的交易结束后选取一定概率的生产者进行检查,如果被检查的生产者这一周期采取了造假的行为,那么会对该生产者进行惩罚,没收其一定比例的财产。其中,抽取生产者的概率叫做监管力度p,没收的财产比例叫做惩罚力度q。

我们使用的参照组模型为初始造假比例为10%的情况,之前的模拟结果显示,稳定后其剩余的不造假者数量只剩下3.99%。而加入惩罚机制后,如图1所示,绿色代表造假者,蓝色代表不造假者。当抽查概率p设定为10%时,与不加入惩罚机制相比,虽然模拟刚开始时差别不大,但是之后加入惩罚机制的模拟中蓝色的方块数量更多,说明该惩罚机制是有效果的。由于p取10%时模型演进到5000周期都没有达到稳定状态,而是在50周期之后,不造假者的数量以一个较低的速率持续增长着。所以我们取前500周期的数据取平均,作为其最终的不造假者数量,结果为6.7%,与不添加惩罚机制的模拟结果相比几乎增加了一倍。

为了进一步观察这种惩罚机制的作用效果,我们用不同的p值做了多次试验,结果显示最终的不造假者数量随着p的升高而逐渐升高,如图2中蓝色点所示。当p取20%时,惩罚机制作用更加明显,这种概率下模型也没有到达稳定状态,用前500周期的平均值算得的不造假者比例为又翻了一倍,达到12.21%;当p取50%时,惩罚机制的效果已经非常明显,在50周期之后基本达到稳定,保持在50%左右。最后,当p取80%时,不造假者的数量最终回升到100%,即造假者不复存在。

对于这个结果——需要抽查概率达到80%才能完全杜绝造假行为,我们依然感到不够满意。因为这个概率在现实生活中是难以达到的,所以我们对惩罚的规则做了一点修改,加入了“连带检查”的机制,即对于发现的造假者,同时对其周围8个人中的造假者也施以同样的惩罚。具体到模拟中,就是在查到造假者之后,同时检查该造假者周围的邻居,如果邻居在这一周期采取了造假的行为,那么也会对其没收相同比例的财产。这是一种更严格的惩罚,而模拟的结果也显示出其更有效果。如图4所示,第三条代表的是加入了“连带检查”的模拟演化图。同样以抽查概率为10%,与前面两种情况相比,第三条的蓝色区域明显增加,并且能够形成较大的片状连接在一起。这种情况下稳定后的不造假者比例达到26.02%。

通过以上两种惩罚机制,以及原有对照组模型的周期演化图,可以更明显看出不同程度惩罚机制的作用。将每种比例下,不同机制的模拟结果放在一张图中,如图5所示,能够更直观的看出每种机制的作用效果。这里的每一个概率下,我们都运行了两种情况,结果差别不大。

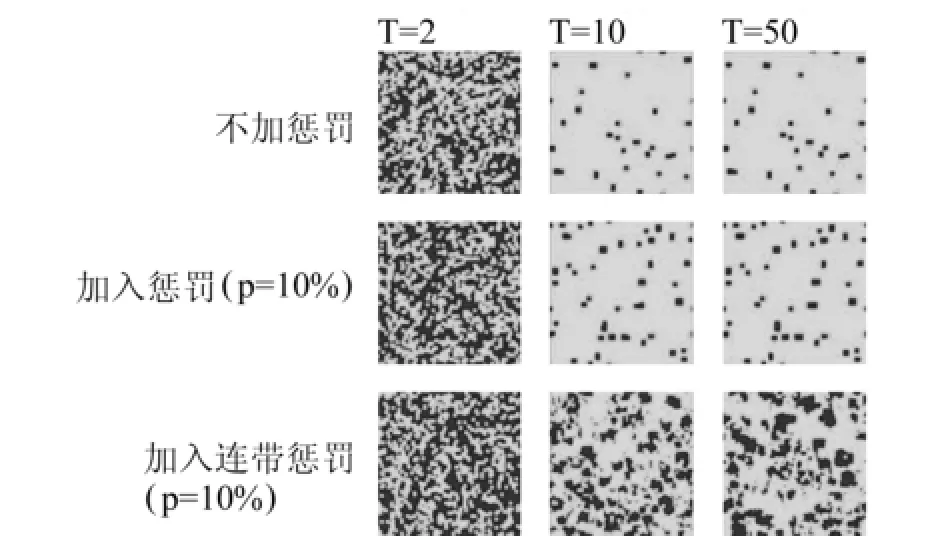
图4 不加惩罚、加入惩罚(p=10%)以及加入“连带检查”(p=10%)三种情况的模拟演化对比图

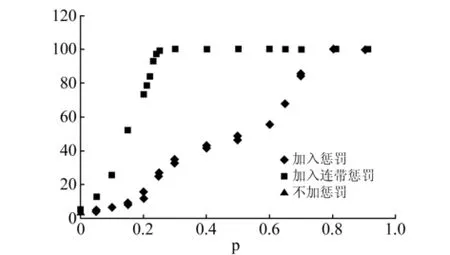
图5 不同监督机制下的最终不造假者数量散点图

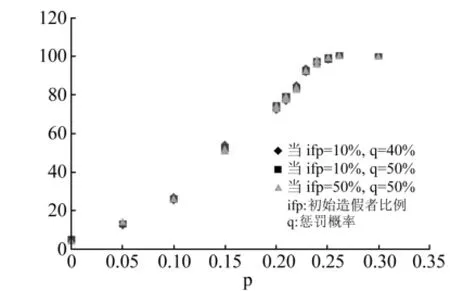
图6 “连带检查”机制中,不同参数下的最终不造假者数量散点图

从上图中可以看出,加入“连带检查”的模型,在抽查概率为26%时即可以消灭所有的造假者,使最终不造假者比例达到100%。如图2所示,相比蓝色的点上涨的速度比较缓慢,红色的点上涨得非常迅速。当p取15%,不造假者的数量即有52%;当p提升到20%时,这时不造假者已经占大多数,达到73%左右;而当p取25%时,几乎全部转化为不造假者,直至p取26%时,最终的比例达到100%。

对于模型的其他参数——初始造假者的比例、惩罚的力度(q)对模型的影响我们也做了研究,结果显示没有明显影响。如下图6所示,蓝色的点代表的是“连带检查”机制下,其他参数不变,将惩罚的比例q从50%改为40%的结果。而图中黄色的点则代表的是,将初始的造假者比例从10%改为50%的情况。作者还尝试了其他多种情况,结果均差异不大。所以可以得出结论,即其他因素对造假行为的影响很小。

四、结论

本文通过对经典的进化博弈模型进行修改,模拟了造假行为传播的过程,并将有无惩罚机制的两种情况进行了对比,找出了最有效果的惩罚机制,即“连带惩罚”。我们在Pavlov模型的基础上,赋予了个体学习的能力,具体表现为比较周围邻居的总收益,然后跟随收益最高者的选择。由于个体在选择时会比较周围邻居的上周期收益,选择其中收益最高者模仿其决策,因此当有个体选择造假时,能够获得较高的额外收益,这一行为能够通过这一博弈过程迅速向外传导,使得他周围的个体都对他进行模仿。结果显示,由于具有学习能力,因此造假行为的传播非常迅速。之后在这个模型之中,我们添加了惩罚机制,即在每个周期的交易结束后选取一定概率的生产者进行检查,如果被检查的生产者这一周期采取了造假的行为,那么会对该生产者进行惩罚,没收其一定比例的财产。模拟的结果显示,抽查的概率是决定性的,造假者的数量会随着这个概率的增加而逐渐减少。

从管理机制的角度,我们的模拟结果为现今的工商执法部门提供了数据依据。要查处造假行为,只需要设定一定的惩罚额度,并尽可能地提高抽查的概率。在实际的打击假冒伪劣的行为中,造假行为往往不是单独发生的,造假者也经常处于聚集状态。对于查到的造假者,如果能做到不仅仅对其实行惩罚,还利用其作为线索继续追查,找出其周围的造假者,不仅能够提高惩罚的震慑作用,也大大降低了执法的成本。

参考文献:

[1] 雷恩·贝德安(2012).管理思想史.北京:中国人民大学出版社.

[2] 刘伟兵、王先甲(2009).进化博弈中多代理人强化学习模型.系统工程理论与实践,3.

[3] 王林燕(2010).中国经济社会诚信缺失现象的文化因素分析——从中国文化诚信观与西方“经济人”假设的角度.河南社会科学,1.

[4] 王先甲、刘伟兵(2011).有限理性下的进化博弈与合作机制.上海理工大学学报,6.

[5] Axelrod R(1984).The Evolution of Cooperation.New York:Basic Books.

[6] A.J.Stewart,J.B.Plotkin(2012).Extortion and Cooperation in the Prisoner’s Dilemma.Proc.Nat.Acad.Sci.USA.

[7] Christian Hilbe,Martin A.Nowak(2012).Karl Sigmund.The Evolution of Extortion in Iterated Prisoner’s Dilemma Games.ar Xiv preprint ar Xiv.

[8] Grilo C,Correia L(2011).Effects ofasynchronism on evolutionary games.Journal of Theoretical Biology.

[9] Harold Koontz(1980).The Management Theory Jungle Revisited.The Academy of Management Review,5.

[10]Herbert Simon(1997).Administrative Behavior.New York:The Free Press.

[11]H.J.Cai(2012).The Historical Context of the Rise of China and the Entry Point of the Transformation of the Development Pattern,Emergence and Transfer of Wealth,2.

[12]H.J.Cai,Yiping Wu(2011).Self-Assertiveness Demands are the Ultimate Cause of Financial Crises,Applied Social Science.Information Engineering Research Institute.

[13]Martin Nowak(2006).Five Rules for the Evolution of Cooperation.Science.

[14]Nowak M A,Sigmund K(1992).Tit for tat in heterogeneous populations.Nature.

[15]Nowak M A,Sigmund K(1993).A strategy of win-stay,lose-shift that out performs tit-for-tat in the Prisoners Dilemma game.Nature.

[16]Parkhe,Rosenthal(1993).Chandran,Prisoner’s dilemma payoff structure in inter firm strategic alliances:an empirical test.OMEGA International Journal of Management Science,5.

[17]Trivers R L(1971).The Evolution of Reciprocal Altruism.The Quarterly Review of Biology,1.

[18]Torsten Röhl,Claudia Röhl(2007).Heinz Georg Schuster,and Arne Traulsen,Impact of fraud on the mean-field dynamics of cooperative social systems,Physical Review,76.

[19]W.H.Press,F.D.Dyson(2012).Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent.Proc.Nat.Acad.Sci.USA.

■责任编辑:刘金波

Fraud Propagations and Containments——A Study Based on Evolutionary Game Simulation Model

Wu Yiping(Doctoral Candidate,Wuhan University)
Cai Hengjin(Professor,Wuhan University)

An evolutionary game model is built up to simulate the fraud behaviors and find a way to better contain them. With modifications the classical Pavlov strategy is changed with learning ability.The simulations depict that the punishment degree doesn’t affect much,on the spread of frand behaviors but the checking frequency is a determining factor.To improve efficiency,the“collateral checking”mechanism is adopted to check and punish the frauds as well as the frauds in their neighborhood.The new mechanism shows better result since it can eliminate frauds at the checking percentage of 26%, while it has to be raised to 80%if without“collateral checking”.

evolutionary game;fraud behavior;punishment method;collateral checking

吴怡萍,武汉大学国际软件学院博士生;湖北武汉430079。Email:wuyp1028@gmail.com。蔡恒进,武汉大学国际软件学院教授,博导。

国家重点基础研究发展计划项目(2011CB302306),武汉大学研究生自主科研项目(201121601020001)