基于局部均值分解的边际谱在滚动轴承故障诊断中的应用

李慧梅，安 钢，黄 梦

（1.装甲兵工程学院机械工程系，北京 100072；2.军事交通学院汽车工程系，天津 300161）

基于局部均值分解的边际谱在滚动轴承故障诊断中的应用

李慧梅1，2，安 钢1，黄 梦1

（1.装甲兵工程学院机械工程系，北京 100072；2.军事交通学院汽车工程系，天津 300161）

局部均值分解（Local Mean Decomposition，LMD）将复杂的多分量信号自适应地分解为有限个乘积函数（PF）的和，在计算了各个分量的瞬时幅值（IA）和瞬时频率（IF）后，可以计算出基于LMD的边际谱。针对直接法求取瞬时频率存在端点误差大问题，提出一种改进的直接求取瞬时频率的方法；提出了基于LMD的边际谱的滚动轴承故障诊断方法，将该方法应用于实际滚动轴承故障诊断中，结果表明该方法能有效地提取出滚动轴承的故障特征频率，从而确定故障部位。

局部均值分解；边际谱；滚动轴承；故障诊断；瞬时频率

滚动轴承是旋转机械中最常用、最易损坏的部件之一，其状态监测和故障诊断一直是一个研究热点。提取滚动轴承的故障特征频率来诊断滚动轴承故障，是滚动轴承故障诊断常用的方法之一［1］。但实际中，由于噪声的干扰，滚动轴承故障特征不明显，这就需要合理的信号处理方法来处理信号，从而突出轴承元件的故障特征频率来诊断故障所在部位。滚动轴承故障振动信号是非平稳信号［2］，为此，应用现代非平稳信号处理方法分析滚动轴承故障振动信号，可更为有效地提取故障特征。小波变换和经验模式分解（EMD）等是滚动轴承常用的非平稳信号处理方法［3－4］。但小波变换分析信号时缺乏自适应性，EMD理论存在模式混叠、端点效应、过包络、欠包络等问题。

2005年，Smith［5］提出了一种新的自适应的时频分析方法——局部均值分解（LMD）。与EMD相比，LMD在抑制端点效应、避免过包络、欠包络、减少迭代次数等方面要优于EMD方法［6］。鉴于这些优点，LMD方法在机械故障诊断中得到了广泛应用，应用最多的是利用它的解调能力来提取故障信息［7－8］，基于LMD的时频谱［9］、能量谱［10］等概念陆续提出并得到应用。但基于LMD的边际谱的应用研究还很少。本文借鉴Hilbert边际谱的思想，给出了基于LMD的边际谱的计算公式；在计算边际谱时，针对直接法求取瞬时频率存在端点误差大的问题，提出了一种改进的直接求取瞬时频率的方法；将基于LMD的边际谱应用于滚动轴承故障诊断中，结果表明该方法能有效地突显出滚动轴承的故障特征频率，从而确定滚动轴承故障部位。

1 局部均值分解方法简介

LMD方法本质上就是将一个信号分解成有限个瞬时频率具有物理意义的乘积函数（PF）分量，其中每一个PF分量都是由一个包络信号a（t）和一个纯调频信号si（t）相乘而得到的，包络信号是该PF分量的瞬时幅值（IA），对纯调频信号的相位展开后求导便可以得到该PF分量的瞬时频率（IF，也记作f（t）），对于一个给定的信号，局部均值分解的具体步骤可参见文献［5］。

一个信号通过局部均值分解后，可获得的主要信号特征如图1所示。通过LMD，原始信号被分解成有限个单分量函数PF，对PF分量的IA和由纯调频信号的相位展开后求导得到的PF分量的IF进行傅里叶变换，可分别得到信号的调幅特征和调频特征。将IA和IF同时显示，即可获得信号完整的时频分布。在此基础上，借鉴Hilbert谱的思想，可获得信号的边际谱、能量谱等。

图1 局部均值分解获得的信号特征Fig.1 The signal characteristics obtained via LMD

2 基于LMD的边际谱

程军圣等［10］定义了基于LMD的时频分布，记作：

式中：n为PF分量的个数；ai（t）为第i个分量的瞬时幅值；fi（t）为第i个分量的瞬时频率。S（f，t）反映了信号幅值随时间和频率的变化关系。

在此基础上，借鉴Hilbert边际谱的思想，定义基于LMD的边际谱为：

S（f）反映了信号的幅值在整个频率段上随频率的变化情况，它的幅值表示信号中某一频率成分在各个时刻的幅值之和。当滚动轴承发生局部损伤时，其故障特征频率必然存在，通过分析边际谱幅值可以找出故障特征频率，从而确定故障部位。

3 一种改进的直接求取瞬时频率的方法

3.1 一种改进的直接求取瞬时频率的方法

为构建基于LMD的时频谱和边际谱，需准确计算各个PF的IA和IF。从局部均值分解的步骤可以看出：在完成分解的同时，就直接计算出了各个PF分量的IA，IF通过分解得到的纯调频信号的相位展开后求导获得，该方法称为“直接法”，这也是局部均值分解的一个优点：不需要进行Hilbert变换就直接计算出了各分量的IA和IF，不会出现无法解释的负频率现象。直接法求取瞬时频率的具体实现步骤可参见文献［11］。但是，直接法在求取瞬时频率时存在端点误差大问题，本文针对该问题提出了一种改进的直接求取瞬时频率的方法。通过仿真信号说明，给定仿真信号：

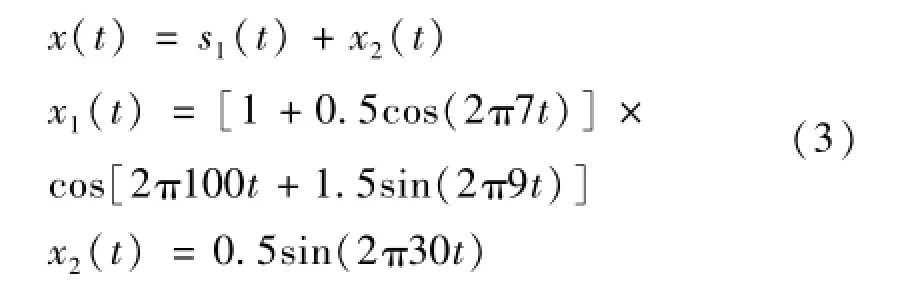
式中：t∈［0，1］，采样频率为1 024 Hz。仿真信号的LMD分解结果如图2所示。从图2中可以看出，PF1对应原信号中的x1（t），PF2对应原信号中的x2（t）。PF3、PF4、PF5是由分解误差产生的伪分量。分别对PF1和PF2利用直接求取瞬时频率的方法计算二者的瞬时频率，结果如图3所示。从图3中可以看出，在信号两端瞬时频率出现了较大误差，见图3中圆圈标注部位，尤其是PF2分量的端点误差较大。

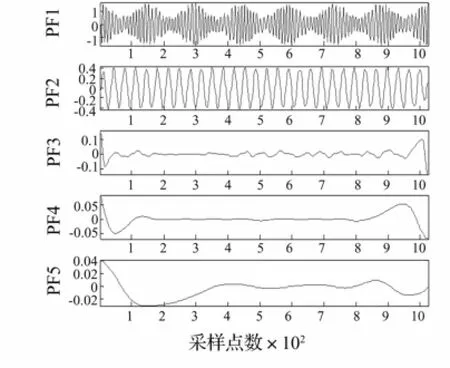
图2 仿真信号的LMD分解结果Fig.2 The LMD results of simulation signal

仿真信号x（t）在t＝0和t＝1时，正好是信号极值点，理论上不存在分解的端点效应问题［11］，所以这里可以排除端点效应带来的原因。但通过分解后，各个分量很有可能在端点处不再是极值点，PF2尤其明显，而与其对应的si（t）在端点处都取值为1或－1，达到极值点。这样的话，就使得si（t）在第一个极值点左边的曲线斜率和最后一个极值点右边的曲线斜率与信号本身不一致，曲线变陡了，见图4中圆圈标注部位，进而造成求得的瞬时相位和瞬时频率在第一个极值点左边和最后一个极值点右边的值与实际信号不符合，发生较大误差。基于上述分析，本文提出一种基于瞬时相位边界波形匹配的改进的直接求取瞬时频率的方法。其具体步骤如下：

（1）对于一个给定的纯调频信号si（t），直接法求取瞬时频率，要求－1≤si（t）≤1，且极大值为1，极小值为－1。若不满足，将所有极大值置1，大于1的值置1；将所有极小值置－1，小于－1的值置－1，使其满足。

（2）求取调整后的纯调频信号的瞬时相位φ（t）＝arccos（si（t）），并对瞬时相位进行边界波形匹配；具体匹配方法见本文的3.2小节。

（3）对匹配后的相位按式（4）展开，并将相位极值点的值去除用临近点的平均值代替，然后进行相位平滑，本文采用Savitzky-Golay平滑滤波器进行相位平滑。

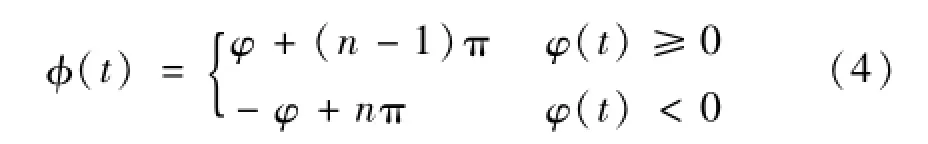
式中：n＝1，2，…，m－1，m是相位极值点个数加2。

（4）对平滑后相位进行求导，得到瞬时频率IF。

为对比分析效果，对仿真信号的PF1、PF2采用改进的直接法计算瞬时频率，结果如图5所示。从图5可以看出，改进后的瞬时频率求取方法可以明显改善原方法的端点误差大问题。

图3 直接法求取的PF分量的瞬时频率Fig.3 PF'IF calculated by directmethod

图4 LMD分解得到的纯调频信号Fig.4 The purely frequencymodulated signals

图5 改进的直接法求取的PF分量的瞬时频率Fig.5 PF'IF obtained by the improved direct

3.2 瞬时相位边界波形匹配方法

匹配包括相位的左右两端，下面以左端匹配为例来说明具体匹配方法。具体步骤如下：

（1）计算瞬时相位第一个极值点左边的点数，记为l；计算瞬时相位的极值点mi（i＝1，2，…，n），n为极值点个数，极值点对应的时间坐标记为tmi。

（2）以第一、二、三个极值点构造一个三角波形，作为特征波形。并计算：

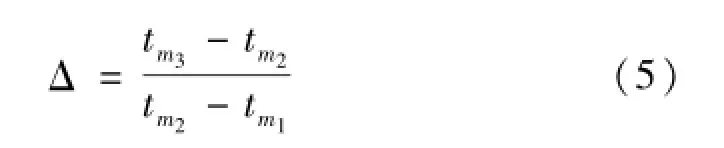
（3）依次以极值点m2k－1、m2k、m2k＋1构造三角波形，若n是偶数，k＝2，3，…，（n－2）／2，若n是奇数，k＝2，3，…，（n－1）／2，并对每个三角波形计算：

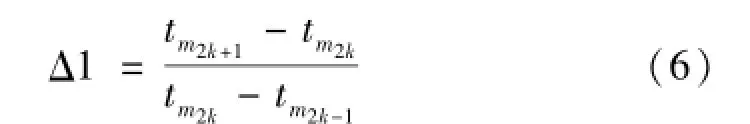
（4）计算各个三角波形与特征波形的匹配误差，匹配误差的计算公式为：δ＝｜Δ－Δ1｜。

（5）找出匹配误差最小的三角波形作为匹配波形，用匹配波形左端的l个点替代第一个极值点左端的点；如有多个匹配波形，则将多个匹配波形左端的l个点对应相加取平均值作为替代值。

（6）按同样的方法匹配最后一个极值点右端的相位，得到匹配后的瞬时相位。区别主要有：特征波形为倒数第一、倒数第二、倒数第三个极值点构造的三角波形；其余三角波形以极值点mn－2k、mn－（2k＋1）、mn－（2k＋2）构造，若n是偶数，k＝1，2，…，（n－4）／2，若n是奇数，k＝1，2，…，（n－3）／2用匹配波形右端点替代最后一个极值点右端的点。

4 应用实例

本文通过电火花电击7216轴承滚动体表面，使其产生长度为3mm，宽度为1mm，深为1mm的凹坑来模拟轴承滚动体点蚀故障，并将该轴承安装在某装甲车辆变速箱主轴上，进行实车行驶试验，采集实车行驶过程中变速箱的振动加速度信号。

试验时，车辆挂三档、发动机转速为1 025 r／min，在平坦水泥路面上匀速行驶。图6是试验时车辆动力传递示意图，其中2为故障轴承。根据变速箱结构，计算出变速箱主动轴转频为24.405 Hz，中间轴转频为12.202 5 Hz，主轴转频为12.202 5 Hz。

图6 某装甲车辆变速箱3档动力传递示意图Fig.6 The 3rd gear power transmission diagram of gearbox

根据7216轴承的几何参数和主轴的转频，由式（7）计算出轴承滚动体故障特征频率为44.91 Hz。

式中：fr为滚动轴承内圈（即主轴）的旋转频率，单位为Hz；d为滚动体直径，单位为mm；D为轴承节径，单位为mm；α为压力角，单位为rad。

图7为采样频率25 kHz，采样点数为4 096点的7216轴承滚动体点蚀故障振动加速度信号的时域波形图。

为了对比，首先采用常用的Hilbert变换包络解调故障诊断方法进行该轴承故障诊断。图8为该轴承故障信号的Hilbert包络谱。为对比清楚，也只画出了0～700 Hz的频率成分。图8中，理论计算特征频率44.91 Hz附近并未出现明显的峰值，反映不出轴承滚动体故障特征频率，这可能是由于信号受到路面随机激励、发动机等部件振动、环境噪声等干扰成分的影响较大，调制信息不明显。解调诊断方法效果不理想，需要考虑新的方法。

采用LMD方法对该振动信号进行分解，其结果如图9所示，其中省略了残余分量。在完成LMD分解的同时，计算出了各个分量的IA和si（t），随后利用改进的瞬时频率求取方法求取各分量的瞬时频率，在此基础上通过式（1）计算出基于LMD的时频分布S（f，t），再通过式（2）计算得到基于LMD的边际谱S（f），如图

图7 轴承滚动体故障信号Fig.7 The bearing fault signal

图8 轴承信号的Hilbert包络谱Fig.8 The Hilbert envelope spectrum of bearing signal

图9 轴承信号的LMD分解结果Fig.9 The LMD results of bearing signal

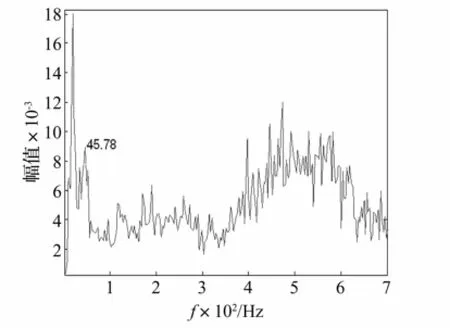
图10 轴承信号的边际谱Fig.10 Themarginal spectrum of bearing signal

10所示。为显示清楚，只画出了0～700 Hz的频率成分。图10清晰地反映了轴承滚动体故障特征频率（45.78 Hz），与理论计算特征频率44.91 Hz基本吻合，从而可以确定该轴承滚动体存在故障。与预先设置的故障一致，说明了方法的有效性。

5 结 论

（1）提出的基于瞬时相位边界波形匹配的改进的直接求取瞬时频率的方法能够有效改善原方法的端点误差大现象，从而提高瞬时频率的计算精度；

（2）基于LMD的边际谱反映了信号的幅值在整个频率段上随频率的变化情况。当滚动轴承发生局部损伤时，其故障特征频率必然存在，通过分析边际谱幅值可以找出故障特征频率，从而确定故障部位及类型；

（3）通过对实际滚动轴承故障振动信号的分析，表明基于LMD的边际谱能有效地应用于滚动轴承故障诊断。

［1］陈亚农，郜普刚，何 田，等.局部均值分解在滚动轴承故障综合诊断中的应用［J］.振动与冲击，2012，31（3）：73－78.

CHEN Ya-nong，GAO Pu-gang，HE Tian，et al.Roller bearing comprehensive fault diagnosis based on LMD［J］.Journal of Vibration and Shock，2012，31（3）：73－78.

［2］康海英，栾军英，郑海起，等.基于阶次跟踪和HHT边际谱的轴承故障诊断研究［J］.振动与冲击，2007，26（6）：1－3.

KANG Hai-ying，LUAN Jun-ying，ZHENG Hai-qi，et al.Fault diagnosis of bearing based on order tracking and HHT marginal spectrum［J］.Journal of Vibration and Shock，2007，26（6）：1－3.

［3］余光伟，郑 敏，雷子恒，等.小波变换在滚动轴承故障分析中的应用［J］.轴承，2011（7）：37－40.

YU Guang-wei，ZHENG Min，LEI Zi-heng，et al.Application of wavelet transform in fault analysis of rolling bearings［J］.Bearing，2011（7）：37－40.

［4］蔡艳平，李艾华，石林锁，等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析［J］.振动与冲击，2011，30（2）：167－172.

CAIYan-ping，LI Ai-hua，SHI Lin-suo，et al.Rolling bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis［J］.Journal of Vibration and Shock，2011，30（2）：167－172.

［5］Smith JS.The localmean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2（5）：443－454.

［6］Wang Y X，He Z J，Zi Y Y.A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis［J］.Journal of Vibration and Acoustics-Transactions of the ASME，2010，132（2）：021010.

［7］Chen B J，He Z J，Chen X F，etal.A demodulating approach based on local mean decomposition and its applications in mechanical fault diagnosis［J］.Measurement Science and Technology，2011，22（5）：1－13.

［8］何 田，林意洲，郜普刚，等.局部均值分解在齿轮故障诊断中的应用研究［J］.振动与冲击，2011，30（6）：196－201.

HE Tian，LIN Yi-zhou，GAO Pu-gang，et al.Application of localmean decomposition in gear fault diagnosis［J］.Journal of Vibration and Shock，2011，30（6）：196－201.

［9］Wang Y X，He Z J，Zi Y Y.A demodulation method based on improved localmean decomposition and its application in rub－impact fault diagnosis［J］.Measurement Science and Technology，2009，20（2）：1－10.

［10］程军圣，杨 怡，张 亢，等.基于局部均值分解的循环频率和能量谱在齿轮故障诊断中的应用［J］.振动工程学报，2011，24（1）：78－83.

CHENG Jun-sheng，YANG Yi，ZHANG Kang，et al.Application of cycle frequency and energy spectrum based on localmean decomposition to gear fault diagnosis［J］.Journal of Vibration Engineering，2011，24（1）：78－83.

［11］任达千.基于局域均值分解的旋转机械故障特征提取方法及系统研究［D］.杭州：浙江大学，2008.

App lication ofmarginal spectrum based on local mean decom position in rolling bearing fault diagnosis

LIHui-mei1，2，AN Gang1，HUANGMeng1
（1.Departmentof Mechanical Engineering，Academy of Armored Force Engineering，Beijing100072，China；2.Department of Automobile Engineering，Academy of Military Transportation，Tianjin 300161，China）

Localmean decomposition（LMD）can be used to decompose a complex multi-component signal into a linear combination of several product functions（PFs）.After obtaining the instantaneous amplitudes and instantaneous frequencies of all PF components，the marginal spectrum based on LMD can be calculated.Aiming at the big error problem of the instantaneous frequency atend-points extracted with the directmethod，an improved directmethod was put forward.Themarginal spectrum method based on LMD for rolling bearing fault diagnosiswas proposed，and itwas applied in actual rolling bearing fault diagnosis.The analysis resultsshowed that the fault characteristic frequency can be extracted effectively，and the fault position can be determined.

localmean decomposition；marginal spectrum；rolling bearing；fault diagnosis；instantaneous frequency

TN911.7；TH165.3

A

军队科研计划项目

2013－01－30 修改稿收到日期：2013－03－11

李慧梅女，博士生，讲师，1978年生