基于问题解决的高等代数课堂教学研究——以极大线性无关组为例

张鑫浩

（镇江高等专科学校丹阳师范学院，江苏丹阳 212300）

基于问题解决的高等代数课堂教学研究
——以极大线性无关组为例

张鑫浩

（镇江高等专科学校丹阳师范学院，江苏丹阳 212300）

将介绍极大线性无关组的2种方式，即从线性无关的向量组引入和从平面向量空间的基底引入，通过设置一连串的数学问题充分融合在一起，可以提高高等代数的教学效率。

问题解决；数学课堂教学；极大线性无关组

1 问题提出

传统的《高等代数》教材非常注重从定义到定理的严谨推理，偏重课程的理论体系［1］。但在具体的课堂教学中，学生由于学习习惯、认知水平等因素的影响，不能快速理解、消化抽象的定义与定理的本质，渐渐就会失去学习的兴趣及动力。因此，在高等代数的教学过程中，不仅要关注逻辑的严谨性和描述语言的准确性，还要关注学生对概念、定义的理解。本文根据支架式教学理论和问题化教学模式，围绕着一个教学单元，通过有意安排一些与课程内容息息相关的问题，与学生共同探讨，培养学生解决问题的认知能力，促进学生高级思维能力的发展，实现他们对课程内容持久深入的理解［2］。

2 教材分析

极大线性无关组是高等代数的核心内容——向量空间中承前启后的一个教学单元。紧密联系着线性相关性和向量空间的基与维数。在不同的教材中，对这部分内容的处理方式、方法差别很大。但总体上，引入的方式主要可以分为从线性无关的向量组引入和从平面向量空间的基底引入两种。不管教材采取何种引入方式，在结构上都是由某点引入，从而构建理论体系，而将其他的引入方式放置在课后习题中。学生对此并不是很理解，学完这部分内容以后，尤其是看了不同版本的教材以后，往往不清楚问题的根源。笔者通过设置一连串的数学问题，在各种处理方式之间寻找一个联系点、平衡点，帮助学生深刻理解。

3 授课过程及设计意图

3.1 概念的引入

问题1已知

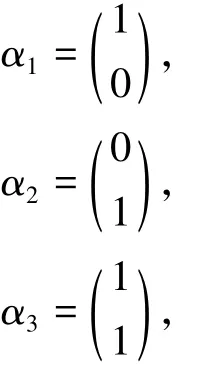
你能写出向量组｛α1，α2，α3｝中含向量个数最多的线性无关的部分组吗？

认真分析问题可知，问题的关键在于写出向量组｛α1，α2，α3｝中所有的线性无关的部分组，可以按照以下步骤进行：

1）写出它的所有的部分组。

2）分别判断它们的线性相关性。究竟是线性相关的，还是线性无关的？

3）写出含向量个数最多的线性无关的部分组。

由此引出极大线性无关组的定义，即

在向量组｛α1，α2，…，αs｝中，我们将其所含向量个数最多的线性无关的部分组称为向量组｛α1，α2，…，αs｝的一个极大线性无关组［3］。

设计意图：由具体问题引出极大线性无关组的概念。这种对极大线性无关组的引入方式与直接定义的方式不同，它突出了“极大”的含义，通俗易懂，可以加深学生对概念的理解。

3.2 性质的探究

在解决问题1的过程中发现其局限性：遇到向量组所含向量的个数较多时，过程很繁琐。因此有必要研究极大线性无关组的性质，由此引出：

问题2向量组（Ⅱ）是向量组（Ⅰ）的一个极大线性无关组，向量组（Ⅱ）有哪些性质？

教师和学生一起探究，总结出极大线性无关组的性质，即

性质1向量组（Ⅱ）是向量组（Ⅰ）的一个线性无关的部分组。

性质2向量组（Ⅰ）中的每一个向量都能由向量组（Ⅱ）线性表出［4］。

进一步引申：

1）向量组与它的极大线性无关组等价。知道这些，在以后研究向量组的时候，可以用它的极大线性无关组去替换它。

2）向量组的极大线性无关组中的每一个向量都不能由其余的向量线性表出，即极大线性无关组中的每一个向量都不能少。因此，极大线性无关组可以形象地描述为原向量组的“浓缩的精华”。

设计意图：学生发现从定义出发寻找极大线性无关组的局限性，会激发他们进一步探索其性质的兴趣，得出极大线性无关组的两条重要性质。通过进一步引申，可以加深学生对这两条性质的理解。

3.3 极大线性无关组的判定

问题3如果向量组（Ⅱ）满足上述两条性质，向量组（Ⅱ）是否为向量组（Ⅰ）的极大线性无关组？

让学生讨论交流，得出结论：

向量组（Ⅱ）满足上述两条性质等价于向量组（Ⅱ）是向量组（Ⅰ）的一个极大线性无关组。

问题4已知

能否找到向量组｛α1，α2，α3，α4｝的一个极大线性无关组？

设计意图：通过问题3进一步探究极大线性无关组的两条性质，证明它们与概念之间的等价关系。并通过具体实例，让学生根据这两条性质寻找极大线性无关组。比较运用概念与运用性质寻找极大线性无关组的不同之处，能让学生在看到不同教材时理解不同定义间的内在联系。

3.4 向量组的秩

问题5向量组的极大线性无关组之间有什么联系？

学生通过探究知道，向量组的极大线性无关组之间是等价的。

由等价的线性无关的向量组所含向量个数相同可知，向量组的所有的极大线性无关组所含向量的个数都相等。

因此，我们将向量组的极大线性无关组所含向量的个数称为这个向量组的秩。引入符号，即将向量组｛α1，α2，…，αs｝的秩记为rank｛α1，α2，…，αs｝。

特别地，若

则｛α1，α2，…，αs｝为线性无关的。

结合极大线性无关组的概念可知，秩为r的向量组中任意r个线性无关的向量都构成它的一个极大线性无关组［5］。这样，我们就能够通过向量组的秩来判断极大线性无关组。

问题6线性表出与向量组的秩之间有什么关系？

师生共同分析出：

命题1若向量组（Ⅰ）能由向量组（Ⅱ）线性表出，则有

rank（Ⅰ）≤rank（Ⅱ）。

特别地，当向量组（Ⅰ）与向量组（Ⅱ）等价时，则

rank（Ⅰ）=rank（Ⅱ）。

设计意图：通过研究问题5得到向量组的秩的概念，并通过向量组的秩来判断、寻找极大线性无关组。通过对问题6的研究，建立线性表出与向量组的秩之间的联系，为向量空间知识的学习奠定基础。

3.5 向量空间的基与维数

以上探讨的向量组，其含有的向量的个数都是有限的，接下来研究向量的个数为无限的情形。

设V是数域F上的一个向量空间，若V中的某向量组｛α1，α2，…，αn｝，也满足两个条件，即1）｛α1，α2，…，αn｝线性无关；2）V中任意向量都可由｛α1，α2，…，αn｝线性表出，我们就称向量组｛α1，α2，…，αn｝就是向量空间V的一个基。向量组｛α1，α2，…，αn｝所含向量的个数称为向量空间的维数。并记为dim V，即dim V=n。

问题7已知

请找出L（α1，α2，α3，α4）的一个基？

通过问题7的解决，我们得到更加一般化的结论，寻找某向量组生成的子空间的基就是寻找该向量组的极大线性无关组。

命题2

dim L（α1，α2，…，αs）=rank｛α1，α2，…，αs｝。

设计意图：由极大线性无关组的研究类比出向量空间的基的概念，同时通过实例使学生理解寻找向量空间的基与寻找向量组的极大线性无关组之间的内在联系。（证明由学生课后完成。）

3.6 维数与秩知识的运用

问题8线性表出、维数与秩的联系？

师生通过对问题8的讨论，得出如下结论：

命题3设U和W都是向量空间V的两个非零子空间，如果U⊆V，则

dim U≤dim W。

命题4若向量组（Ⅰ）能由向量组（Ⅱ）线性表出，则有

rank（Ⅰ）=dim L（Ⅰ）≤dim L（Ⅱ）=rank（Ⅱ）［6］。

特别地，当向量组（Ⅰ）与向量组（Ⅱ）等价时，则有rank（Ⅰ）=dim L（Ⅰ）=dim L（Ⅱ）=rank（Ⅱ）。

设计意图：从向量组之间的线性表出关系，推出各自生成子空间之间的包含关系，即命题3。再联系向量组的秩就是生成子空间的维数，得到命题4。

3.7 探究拓展

课堂上主要讨论有限维向量空间。对于有限维向量空间的基的存在性，留给学生课后思考。

4 结束语

紧紧围绕如何寻找向量组的极大线性无关组，依次得到了极大线性无关组的定义、性质以及向量组的秩。再运用类比方法，从有限个向量的向量组过渡到向量空间，依次得到向量空间的基与维数，以及如何寻找向量空间的基。通过实例归纳向量空间的基、维数与向量组的极大线性无关组、秩之间的联系。最后，阐述向量组的线性表出运用秩与维数的知识，加深学生对线性表出的理解。

［1］陈建华，李立斌，凌智，等.基于问题解决的线性代数课程教学设计研究［J］.高等理科教育，2011（4）：117-119.

［2］胡小勇.问题化教学设计［D］.上海：华东师范大学，2005：11-13.

［3］张贤科，许甫华.高等代数学［M］.北京：清华大学出版社，2004：75.

［4］张禾瑞，郝鈵新.高等代数［M］.北京：高等教育出版社，2007：226.

［5］丘维声.高等代数（上）［M］.北京：高等教育出版社，2007：79.

［6］唐忠明，戴桂生.高等代数［M］.南京：南京大学出版社，2000：113.

〔责任编辑：卢 蕊〕

A study of classroom teaching of Higher Algebra based on solving problems—Taking themaximal linearly independent group for examp le

ZHANG Xin-hao
（Danyang Normal School，Zhenjiang College，Danyang 212300，China）

According to the teaching problems in the teaching of Higher Algebra and besed on the teaching practice，the current twoways to introduce themaximum linearly independentgroup，that is introduced from linearly independent group or from the basal plane vector，are fully fused together by setting a series ofmathematical problems to improve the teaching effectiveness of Higher Algebra.

solving problem；mathematics classroom teaching；maximum linearly independent group

O15-4

C

1008-8148（2014）03-0104-03

2014-02-15

张鑫浩（1975—），男，江苏丹阳人，讲师，硕士生，主要从事数学教育、代数几何研究。