步进炉控温系统传感器容错控制研究
2014-05-25胡玲艳王兴成
胡玲艳 王兴成
(大连海事大学信息科学技术学院1,辽宁 大连 116026;大连大学信息工程学院2,辽宁 大连 116622)
步进炉控温系统传感器容错控制研究
胡玲艳1,2王兴成1
(大连海事大学信息科学技术学院1,辽宁 大连 116026;大连大学信息工程学院2,辽宁 大连 116622)
针对冶金领域大型步进炉内部测温传感器可能出现的不同故障状态,引入多模态故障模型;考虑系统存在的时滞及不确定性因素,基于李雅普诺夫稳定性定理及LMI方法,进行鲁棒稳定性分析及容错控制器设计,得到在任意传感器故障情况下保证系统稳定的充分条件。最后根据辨识得到的系统模型,借助Matlab的LMI工具箱进行仿真研究,结果表明所得定理能够保证系统具有鲁棒完整性,验证了所得定理的有效性。该研究为实际生产过程的优化控制提供了有力的指导依据。
步进炉 时滞 不确定性 容错控制 LMI
0 引言
步进炉热处理过程是一个典型的复杂工业过程控制系统,内部工艺环节多、控制难度大,业内专家、学者一直对该类炉型设备先进控制技术进行研究。他们从不同的角度提出新的控制理论及研究方法,这也为其他复杂工业过程的控制研究提供了有效参考。
对步进炉控制技术的研究不仅出于节能降耗的实际需要,同时也是对计算机控制技术和智能化综合控制方法的研究与实践。本文以宁夏中色某集团公司所建一座铜扁锭天然气步进式加热炉为研究背景,考虑系统运行过程中存在的不确定、滞后特性,以及不同传感器可能出现的故障状态,参考基于热传导和能量平衡方程所建立的炉温状态空间模型,进行鲁棒容错控制器设计,以增强系统的适应性、可靠性。
1 系统模型
1.1 系统温度分布模型
步进式加热炉主要为铜及铜合金锭进行加热,采用端进、端出步进式结构,从进料端到出料端分为余热回收段、加热段、保温段。由于炉型较大,为提高系统控温的均匀性,加热段、保温段又分为多区进行控制。炉子内部分区如图1所示。
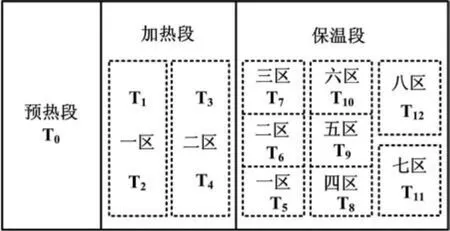
图1 步进炉内部分区及测温点示意图Fig.1 Interior partitions and temperature measurement points in stepping furnace
在系统控制过程中,各区温度通过热电偶进行检测。预热段不做控制,只设一支热电偶T0实时进行温度监控。加热段和保温段是控制段,加热段分为两区,两区单独控制,加热一区设两个热电偶温度检测点T1和T2;加热二区设两个热电偶测温点T3和T4。在保温段,为保证控温精度及温度分布的均匀性,分区进一步细化,共分为八个控温区,各区分别设一支控温热电偶。图1中虚线所进行的分区是软件上的虚拟分区,是程序控制上的划分。在满足工艺控制要求的前提下,分区也可采用其他形式[1]。
针对上述步进炉控制工艺,以文献[1]和[2]推导得到的状态空间模型为参考,以铜锭温度为状态向量X,炉温为控制向量U,根据离散状态空间模型与连续状态空间模型之间的转换关系,考虑实际系统的状态不确定性与时滞性,给出如下铜锭温度分布状态空间模型[1-2]:

式中:状态变量x∈Rn为铜锭温度;控制变量u∈Rm为炉温;A∈Rn×n、B∈Rn×m为根据工艺参数辨识后的常数矩阵;τ为系统时滞;ΔA、ΔAd为系统运行过程中存在的状态不确定性与时滞不确定性。
假设ΔA、ΔAd满足如下条件:

式中:D、E和Ed分别为具有适当维数的常值矩阵。H(t)满足:

1.2 故障模型
假设在各区段对温度的检测过程中,考虑热电偶及温度变送器可能出现的故障或失效状态,引入故障矩阵S。S为对角矩阵,表达式如下:

式中:si为某控温区第i个传感器运行状态。
si为1代表热电偶及变送器工作正常,si为0代表断路故障或无信号,si<1代表传感器检测信号小于实际值,si>1代表传感器信号被放大,即大于实际值[3]。故障模式如表1所示。
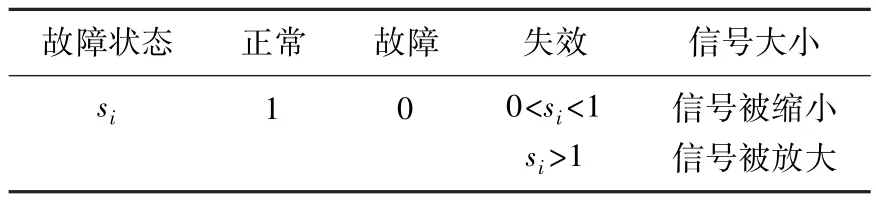
表1 故障模式Tab.1 Fault modes
2 稳定性分析及控制器设计
针对模型存在的不确定性、时滞性及传感器故障情况,下面进行系统的稳定性分析和容错控制器设计。首先给出如下引理。
引理1[4-5]假设X、Y和H是具有适当维数的已知常数矩阵,且满足≤I和α>0,P∈Rn×n,如果P正定,则:

引理2[4](Schur Complement引理)对于对称矩阵A11、A22和A12,以下条件是等价的:
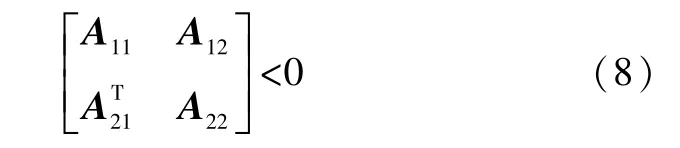
下面针对系统(1)构造变增益状态反馈控制器:
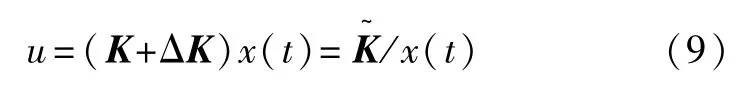
式中:K为反馈增益矩阵;ΔK为增益摄动。
这里考虑摄动是由于控制器性能衰减所导致的情况[5],则ΔK=δK。

式中:δj为不确定参数。

将式(9)代入系统(1)中,则闭环系统为:

将传感器故障矩阵S引入式(12),则S=diag(s1, s2,…,sm)应放在状态变量x与之间[6-8],于是闭环系统模型可写为:

定理:考虑系统(13)可能存在的各种传感器故障,给定标量α>0,如果存在矩阵和适当维数的正定矩阵P,满足如下矩阵不等式,则系统(13)是渐进稳定的。

证明 对任意的传感器故障,选择如下Lyapunov函数。

式中:P为正定矩阵;Q为半正定待定矩阵。
设V1(x,t)=xT(t)Px(t),将其沿闭环系统(13)求导可得:
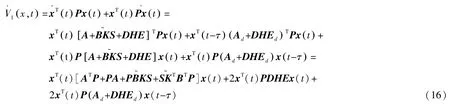
根据引理1,可以得到:

定义:

由式(16)~(19),求V(x,t)导数得到:
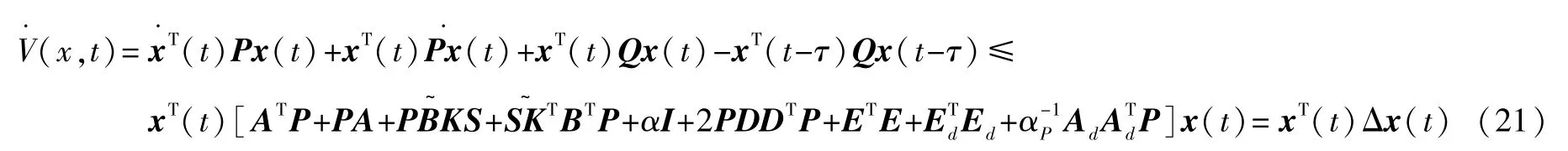
于是有:
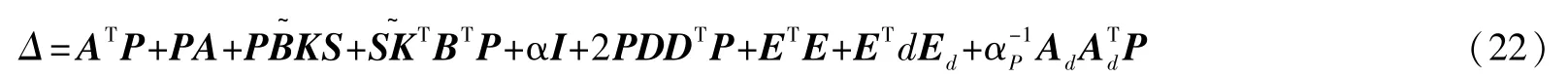

根据引理2,可知式(23)与式(13)是等价的,证明完毕。
3 参数辨识及仿真
定理1 推导及证明过程给出了系统(1)稳定的条件及容错控制器的设计形式,下面以步进炉加热一区为例,采用文献[2]对系统模型进行离散化处理的技术。针对青铜锭多批次的运行过程进行数据采集,借鉴文献[1]~[2]模型辨识方法,获得如下统计参数值:青铜锭厚度0.22 m、Ka=24.8、ρ=8 800 kg/m3、C= 343。取沿炉长方向的单元步长Δy=0.02 m,铜锭平均运行速度v=0.05 m/s,h(i,k)辨识值约为36.8。经矩阵变换可得到辨识矩阵。


当α=0.3、τ=2 s时,考虑加热一区可能的温度传感器故障状态,设S0=diag(1,1)代表两个传感器均正常,S1=diag(0,1)代表第一个传感器T0故障,第二个传感器T1正常;S2=diag(1,0)代表第一个传感器T0正常,第二个传感器T1故障;利用Matlab的LMI工具箱,求解由S0、S1、S2构成的线性矩阵不等式,可得:

假设控制器衰减造成的扰动δ=diag[0.2,0.2],,则:

设初始状态x(0)=[5.0 -0.46]T,α=0.3,τ= 2 s,经仿真,系统的零输入响应如图2所示。
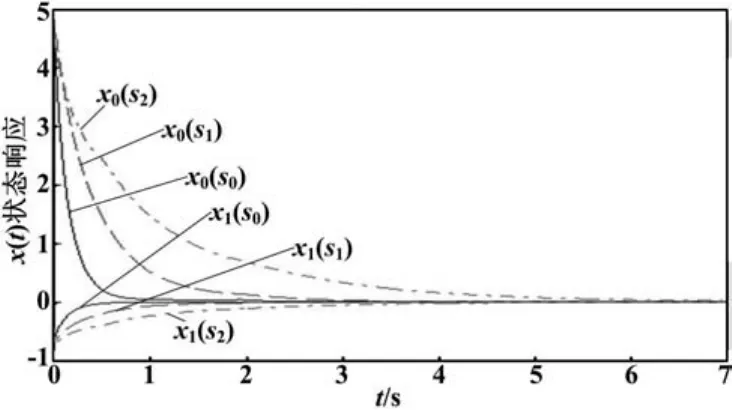
图2 s0,s1,s2时不同故障下零输入响应曲线Fig.2 State response curves of x with s0,s1,s2
当传感器处于失效状态,假定初始状态与图2相同,设α=0.6,τ=4s,取s3=diag(0.15,1),即第一测温传感器检测值小于实际值;取s4=diag(3.5,1),即第一个传感器检测信号大于实际值。经仿真系统的零输入响应如图3所示。
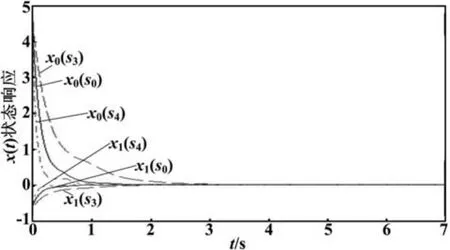
图3 s0,s3,s4时不同故障下零输入响应曲线Fig.3 State response curves of x with s0,s3,s4
由图2和图3可见,系统状态向量X0和X1分别从初始值5.0和-0.46逐渐趋向于零,这就表明在各种故障状态下,定理1及容错控制器能够保证系统具有鲁棒完整性[6-8]。
4 结束语
步进炉控制系统的稳定性及容错能力是提高系统控制品质的重要体现,也是先进控制算法优化系统控制的目标。本文基于步进炉状态空间模型,针对系统存在的不确定、时滞性及传感器故障情况进行鲁棒容错控制设计,得到了系统稳定条件及容错控制器设计结构,仿真结果验证了算法的正确性。该控制算法对冶金领域同类炉型设备具有一定普适性,具有较强的实践意义和推广研究价值。
[1] 田玉楚,侯春海.连续热镀锌退火炉的数学模型开发[J].冶金能源,1995,14(3):38-41.
[2] 田玉楚,侯春海.带钢连续热镀锌退火过程的模型化[J].控制理论与应用,1995,12(4):459-463.
[3] 宗臻,王诗宓.基于LMI的输出反馈鲁棒完整性控制器设计[J].控制理论与应用,2005,22(3):682-686.
[4] 吴敏,何勇.时滞系统鲁棒控制[M].北京:科学出版社,2009.
[5] 陈跃鹏,周祖德.广义系统的鲁棒控制与容错控制[M].北京:科学出版社,2010.
[6] 马喜成,李炜,薛芳.基于时滞状态反馈的鲁棒容错控制[J].控制工程,2007,14(6):668-672.
[7] 马喜成,李炜.不确定时滞系统的鲁棒容错控制[J].兰州理工大学学报,2007,33(3):79-82.
[8] 杨虹,孙金生,王执铨,等.不确定离散时滞系统的鲁棒容错控制器的设计[J].控制工程,2004,11(7):132-135.
Research on the Sensor Fault Tolerant Control for Temperature Control System of Stepping Furnace
Due to different fault states of the temperature sensors may appear in large scale stepping furnaces of metallurgical field;the multimodal fault model is introduced.Considering time delay and uncertainty exist in the system,based on Lyapunov stability theorem and linear matrix inequality(LMI)method,the robust stability is analyzed and the fault tolerant controller is designed,thus the sufficient conditions to guarantee stability of the system under any sensor fault are derived.In accordance with the system model obtained by recognition,and with help of the LMI toolbox of Matlab,simulation research is conducted.The results indicate that the approach obtained can ensure the robust integrity and verify the effectiveness.The study provides useful guiding significance to optimal control for practical production processes.
Stepping furnace Time-delay Uncertainty Fault-tolerant control Linear matrix inequality(LMI)
TF345
A
2010辽宁省教育厅重点实验室基金资助项目(编号:LS2010007);
2013辽宁省教育厅科学研究基金资助项目(编号:L2013463)。
修改稿收到日期:2013-12-10。
胡玲艳(1978-),女,现为大连海事大学控制理论与控制工程专业在读博士研究生,副教授;主要从事先进智能控制、热处理过程工业控制算法的研究。
