正弦输出磁编码器在线分步校正方法
2014-05-25张健龚丽农
张健 龚丽农
(青岛农业大学机械电子工程学院,山东 青岛 266109)
正弦输出磁编码器在线分步校正方法
张健 龚丽农
(青岛农业大学机械电子工程学院,山东 青岛 266109)
磁编码信号往往存在直流偏置、幅值不等和相位偏移等问题,需要对其进行校正。为解决Hydemann校正方法参数选择困难的问题,提出了一种在线分步校正方法。采用数字峰峰值检测算法,获取磁编码器输出信号的幅度及直流偏置;采用简化的Hydemann方法获取相移信息。试验结果表明,该算法响应速度快、校正精度高、参数选择容易、便于计算机的实现,具有一定的工程应用价值。
磁编码器 直流偏置 幅值不等 相位偏移 校正 峰峰值检测
0 引言
磁编码器是一种基于磁阻效应或霍尔效应的新型轴角传感器,具有结构简单、体积小、抗冲击能力强、可靠性高[1-3]等特点,被广泛应用于工业、农业以及航天领域。磁编码器的输出是转子角位置的正余弦信号[4]。但由于众多非理想因素的影响,磁编码器输出的正余弦信号往往存在直流误差、幅值误差和相位误差。若直接进行解调,必将造成较大的解调误差,需先对其进行校正。最常用的校正方法为Hedemannn方法[5-8],但其对初值选择要求较高;另外,锁相环法[9]、傅里叶分析法[10]、神经网络法[11]以及非线性校正方法[12]也有较广泛应用。
为解决常规Hedemann方法迭代初值选择困难的问题,本文提出了一种分步的在线磁编码器输出信号校正方法。该方法采用动态峰峰值检测方法获取正余弦信号的直流偏置及幅值;利用所获取的幅值及偏置信息,构造简化的目标方程,采用梯度算法获取相移信息。
1 磁编码器工作原理
单对极磁编码器的基本结构是在单对极永磁磁鼓下方的平面内,垂直放置A、B两个磁敏元件,如图1所示。当永磁磁鼓随着旋转装置旋转时,周围空间将产生正弦分布的旋转磁场,磁敏感元件感知磁敏感强度变化后,输出包含角位置信息的电压信号。

图1 单对极磁编码器基本结构图Fig.1 Basic structure of the magnetic encoder with single pair of pole
理想情况下,磁编码器的输出是完全正交的正余弦信号,但是由于制造工艺的影响,实际的正余弦信号中往往存在幅值不等、直流偏置和相位偏移问题。此时,若直接对磁编码器输出信号进行解调(常用方法包括反正切法、锁相环法等),必将造成较大的解调误差,因此对磁编码器输出信号进行校正是很有必要的。
2 磁编码器输出信号校正方法
本文所提出的补偿算法流程框图如图2所示。

图2 校正方法流程框图Fig.2 Flowchart of the proposed correction method
磁编码器输出信号ysin、ycos经滤波及幅值调理后,得到调理后正余弦信号ys、yc。
假设ys、yc可以描述为:
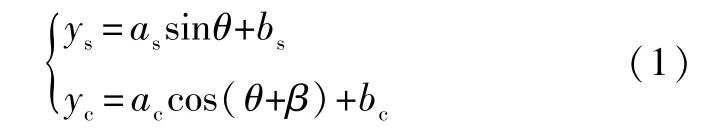
式中:as、ac为幅值增益系数;bs、bc为直流偏置量;β为相位偏移角。借鉴Hedemannn方法,若定义x1=1/ac, x2=-bc/ac,x3=1/(as×cosβ),x4=-bs/(as×cosβ)-bctanβ/ac,x5=tanβ/ac,式(1)可改写为:
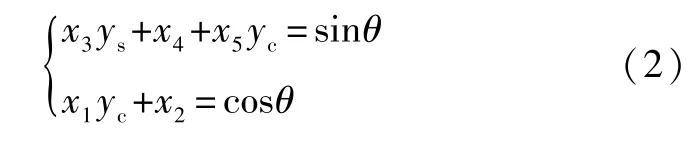
因此,若能获取as、ac、bs、bc及相移β信息,便可通过式(2)对磁编码器输出信号进行校正,得到完全正交的两路正余弦信号。
记ys、yc经A/D转换可得其数字量ys[k]、yc[k]。如图2所示,通过幅值及偏置计算可获取ys、yc的幅值增益系数as、ac及直流偏置量bs、bc;相移β信息由相移估计算法利用ys[k]、yc[k]、幅值增益系数as、ac及直流偏置量bs、bc信息经过多次迭代获取;然后,利用式(2)对ys[k]、yc[k]进行整定,便可得到正交的数字正余弦信号;最后经D/A转换后,可得正交的模拟正余弦信号
2.1 幅值及偏置计算
定义ys[k]、yc[k]的峰-峰值(最大值与最小值)分别为ysmax、ycmax与ysmin、ycmin。当A/D采样率远远高于磁编码器输出信号频率时,由采样时间所造成的峰-峰值检测误差可近似忽略。因此,ys、yc的幅值增益系数as、ac及直流偏置量bs、bc计算公式为:

2.2 相移估计
根据x1~x5的定义,若ys、yc的幅值增益系数as、ac,直流偏置量bs、bc及x1、x2为已知量,则x4可由x3、x5线性表示为:

因此,式(2)可简化为:
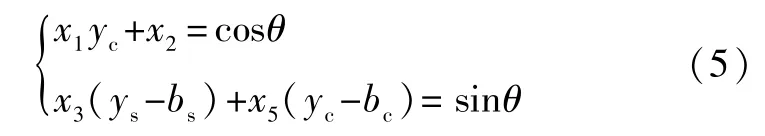
定义M=[ys-bsyc-bc],X=[x3x5]。根据三角函数性质cos2θ+sin2θ=1及式(5)可得:

选取目标函数为:
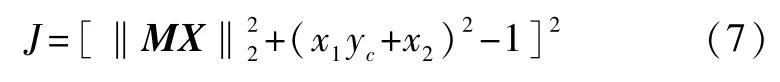
选取Lyapunov函数为:

式中:▽J为J的梯度。

根据Lyapunov稳定性理论,只需取:

J将收敛至零。为便于计算机实现,式(11)可离散化为:

式中:J[k]、▽J[k]为第k时刻目标函数J的值;η为大于零的合适数。
目标函数(7)为二元二次方程,其必然存在符号相反的两组解,即根据迭代初值的选取不同,将获取符号相反的两组x3、x5。但是磁编码器输出信号的相移-90°<β<90°,因此根据x3的定义,x3为正值的一组解为其真解。若迭代结果x3为负数,则对所得x3、x5取反,即得真解。获取x3、x5的估计值后,由x5的定义,通过反正切运算便可得到相移β,通过式(2)便可得到校正后的磁编码器输出信号sinθ和cosθ。
3 试验结果及分析
为验证本文方法的有效性,进行了实物试验验证。在试验装置中,算法由DSP芯片TMS320F28335实现,其主频可达150 MHz,具有浮点数及三角函数运算功能。A/D转换采用DSP内置A/D模块完成,采样率高达15 MHz,分辨率为12位,并支持两路信号同步触发功能。D/A转换芯片采用TI公司DA7664,其转换精度可达16位,转换时间可达12 μs,并支持同步锁存输出功能。磁编码器输出信号如图3所示(为便于与校正后信号比较已通过硬件电路进行了归一化)。

图3 磁编码器输出信号曲线Fig.3 Output signals curves of magnetic encoders
由图3可知,校正前信号存在明显的幅值不等、直流偏置问题。由于DSP内置A/D模块所能接收的模拟信号范围为0~3.3 V,因此还需对图3所示磁编码器输出信号进行正向偏置(约1 V)。DSP所接收到的磁编码器输出信号如图4所示。

图4 DSP接收到的磁编码器输出信号曲线Fig.4 Output signals curves of magnetic encoder received by DSP
采用峰-峰值检测方法所获取的ys、yc的峰-峰值ysmax=2.091 0 V、ysmin=0.133 4 V、ycmax=2.244 7 V、ycmin= 0.020 3 V。记Heydemann方法为CM1,本文所述方法为CM2,CM2,ac、bc、bs和B估计值如表1所示。

表1 CM2,ac、bc、as、bs和β估计值Tab.1 Estimated values of ac、bc、as、bsand β of CM2
由x1、x2的定义可得x1=0.987 9、x2=-1.118 9。将获取的x1、x2、bs、bc及ys[k]、yc[k]代入相应公式,选取η=0.001,迭代初值X=[1 0.1],进行迭代,得x3=1.034 9、x5=0.159 7。x3、x5迭代过程如图5所示。根据x5定义,得tanβ=0.161 6,取其反正切,得β= 9.179 6°。
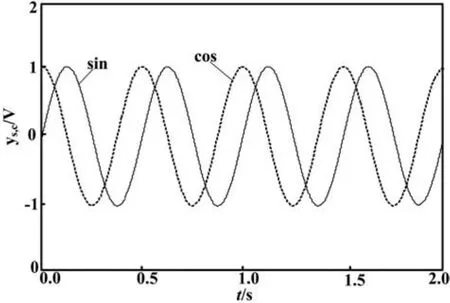
图5 X迭代过程曲线Fig.5 Convergence process of vector X
将获取的磁编码器输出信号幅值增益系数as、ac,直流偏置量bs、bc及相位偏移β代入式(2),得校正后的磁编码器输出信号如图6所示。校正前后磁编码器输出信号的李沙育图形如图7所示,由图可见,校正后的两路信号的已基本正交。

图6 校正后磁编码器信号曲线Fig.6 Output signals of magnetic encoder after correction

图7 校正前后两路信号的李沙育图形Fig.7 Comparison of Lissajous figures before and after correction
为验证本文所述方法对迭代初值选取的鲁棒性,对x3、x5的迭代收敛情况进行试验,并与Heydemann方法进行了比较。试验结果如表2所示。
由表2可知,由于Heydemann方法目标函数存在多解问题,当x3、x5选取不同的迭代初值时,会收敛至不同值,而本文所述方法将收敛至唯一解。

表2 CM1与CM2参数收敛情况比较Tab.2 Comparisons of parameters convergence conditions of CM1and CM2
4 结束语
本文针对磁编码器输出信号中存在的幅值不等、直流偏置及相位偏移问题,提出了一种在线的分步校正方法。首先采用数字峰-峰值计算方法获取幅值不等及直流偏置信息,然后采用简化的Heydemann方法获取相位偏移,并采用DSP作为主控CPU进行了实现。试验结果表明,采用数字峰-峰值计算方法能够准确获取直流偏置信息;采用简化的Heydemann方法,目标函数仅包含符号相反的两组解,迭代结果不受迭代初值影响,参数选择更加容易。
[1] 姜芳芳.基于DSP的单对磁极磁编码器[D].沈阳:沈阳工业大学,2013.
[2] 张立化,吴红星,郑继贵,等.基于工业机器人用位置伺服磁编码器的设计[J].微电机,2013,46(10):56-60.
[3] 季学武,何正义,张雪峰.磁旋转编码器在永磁同步电机位置测量中的应用[J].电气传动,2008,38(2):6-8.
[4] 于非,赵继敏,罗响.磁编码器算法分析与研究[J].微特电机, 2011(10):20-25.
[5] Heydemann P L M.Determination and correction of quadrature fringe measurement errors in interferometers[J].Applied Optics, 1981,20(19):3382-3384.
[6] Kang H J,Kim S H,Lee S H et al.Adaptive digital demodulation of sinusoidal encoder signal for positioning control of spiral servo track writing[J].Microsystem Technologies,2012(18):1247-1253.
[7] Balemi S.Automatic calibration of sinusoidal encoder signals[C]// Proceedings of the 16th IFAC World Congress.Prague:IFAC,2005: 68-73.
[8] Van H H,Jeon J W.Signal compensation and extraction of high resolution position for sinusoidal magnetic encoders[C]//Control, International Conference on Automation and Systems 2007.Korea: ICROS,2007:1368-1373.
[9] Van H H,Jeon J W.An efficient approach to correct the signals and generate high-resolution quadrature pulses for magnetic encoders[J]. IEEE Transactions on Industrial Electronics,2011,58(8):3634-3646.
[10] Faber J.Self-calibration and noise reduction of resolver sensor in servo drive application[C]//ELEKTRO 2012,Rajeck Teplice: IEEE,2012:174-178.
[11] Tan K K,Tang K Z.Adaptive online correction and interpolation of quadrature encoder signals using radial basis functions[J].IEEE Transactions on Control Systems Technology,2005,13(3):370-377.
[12] 曾一凡,李蕊.单对磁极磁编码器的信号处理方法[J].仪表技术与传感器,2012(7):9-15.
An Online Step-by-step Correction Method for Sinusoidal Output Magnetic Encoders
Very often,the magnetic encoding signals are featuring with DC offset,unequal amplitudes,and phase shift,etc.,so it is necessary to correct the signals.In order to solve the problem of Hydemann correction method about difficult to select parameters,an online step-to-step correction method is proposed.By adopting digital peak-peak value detection algorithm,the amplitude and DC offset of the output signals of magnetic encoder are obtained,and the phase shift information is got by adopting simplified Hydemann method.The result of tests shows that the algorithm features fast response,high correction accuracy,easy to select parameters,and convenient to be implemented by computer,it possesses certain engineering applicable values.
Magnetic encoder DC offset Amplitude deviation Phase shift Correction Peak-peak detection
TM383
A
修改稿收到日期:2014-04-25。
张健(1982-),男,2006年毕业于山东科技大学测试计量技术及仪器专业,获硕士学位,讲师;主要从事伺服电机控制的研究。
