石英挠性加速度计零偏分析与建模方法
2014-05-25王洪李磊民黄玉清
王洪 李磊民 黄玉清
(西南科技大学信息工程学院1,四川 绵阳 621000;西南科技大学国防科技学院2,四川 绵阳 621000)
石英挠性加速度计零偏分析与建模方法
王洪1李磊民2黄玉清1
(西南科技大学信息工程学院1,四川 绵阳 621000;西南科技大学国防科技学院2,四川 绵阳 621000)
针对温度、振动、湿度等因素会影响石英挠性加速度计的参数漂移这一问题,对石英挠性加速度计在贮存条件下的稳定性进行了研究。首先在贮存条件下采集石英挠性加速度计的零偏数据,分析数据特点及规律,然后建立时间序列数学模型,最后对模型进行进行仿真。将贮存条件下的真实数据和预测数据进行对比,对比结果表明建模是有效的,建模所得数据的相对误差在允许误差范围内,证明了建模的适用性。预测数据反映了在贮存条件下零偏数据随周围环境变化的规律,为研究石英挠性加速度计在贮存条件下的稳定性提供了理论参考。
时间序列模型 石英挠性加速度计 零偏数据 自回归滑动平均模型 数据分析
0 引言
石英挠性加速度计是高精度探测与控制仪器,在航空、航天和航海业的导航、定位系统中具有不可替代的作用,是导弹、核潜艇、远程轰炸机等战略武器的核心器件[1-2]。然而在贮存条件下,温度、振动、湿度、外磁场干扰等诸因素的影响会引起加速度计的参数漂移,具体表现为零偏K0与标度因数K1的变化,进而造成严重的导航计算误差[3]。因此,在贮存条件下,对石英挠性加速度计进行稳定性分析和建立正确的数学模型分析其稳定性是研究的重点。文献[4]采用有限元仿真与物理试验试验相结合的方法,初步探索温度对石英挠性加速度计的热致变形误差影响规律[4]。文献[5]通过大量的重复性静态试验试验测试,分析了石英挠性加速度计的误差来源,并建立了导航系统定位精度误差补偿的数学模型[5]。文献[6]选择自回归滑动平均模型,对时间序列数据进行模型的建立和仿真[6]。
本文通过在贮存条件下对石英挠性加速度计零偏数据的采集,分析零偏数据的特点和变化规律,得到贮存条件下石英挠性加速度计零偏的时间序列数据;并对数据建立自回归滑动平均模型,通过该模型对石英挠性加速度计零偏数据进行短期预测。建模结果表明,时间序列模型分析法对石英挠性加速度计的稳定性分析具有一定的有效性。
1 零偏数据采集和分析
1.1 零偏数据采集
石英挠性加速度计是用石英晶体经过特种加工形成挠性支撑,并用电容元件作为信号传感器,也就是用力矩器磁钢的表面与敏感质量两边平面之间的间隙变化来拾取摆质量相对壳体的位移信号。当敏感质量在加速度作用下产生偏转时,由于两边间隙的改变使桥路容抗发生变化,从而输出反映摆偏转角的信号[5]。
考虑到采集零偏数据是一个长期且繁琐的工作过程,因此设计一个数据采集装置,其模型如图1所示。以0°为起点,按照旋转角度45°为间隔,测量加速度计在360°之内各个姿态下的零偏数据,以此得到零偏时间序列数据。
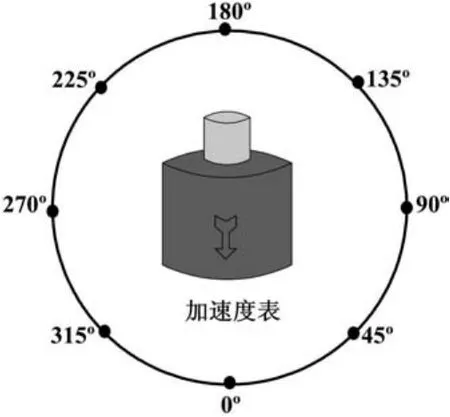
图1 石英挠性加速度计数据采集模型Fig.1 The data collecting model of quartz flexible accelerometer
1.2 零偏数据分析
零偏值是指在确定性误差恒定的加速度条件下,偏离0电压的值。对于石英挠性加速度计来说,输入加速度值与输出电量间的关系式为[1-2]:

式中:Ain为石英挠性加速度计输出所指示的加速度,以重力加速度g为单位,g=9.8 m/s2;U为石英挠性加速度计的输出电压;K0=(U0+U180)/2K1,为零偏值; K1=(U90-U270)/2为电压标度因数;K2=(U90+U270)/ 2K1-K0为二阶非线性系数;x为输入加速度。
石英挠性加速度计在贮存条件下,结合式(1),每隔10 d在正常试验试验条件下采集51个零偏数据,得到的51个离散时间序列如表1所示。

表1 石英挠性加速度计的零偏数据Tab.1 The zero offset data of quart flexible accelerometer 10-6g
2 零偏数据时间序列模型建模
2.1 自回归滑动平均模型
假设{Xt}为随机时间序列,Box-Jenkins模型理论认为xt的取值不仅与前p步的各值xt-1,xt-2,…,xt-p有关,而且同前q步的随机干扰at-1,at-2,…,at-q也有关,且均为线性关系,从而得到自回归滑动平均模型ARMA(p,q)的模型如下[7]:

式中:xt为时间序列数据经过d阶差分处理后的平稳数据序列。
这一模型就称作p阶自回归q阶滑动平均混合模型,记为ARMA( p,q)模型。若p=0,称作纯滑动平均模型,记为MA( q);若q=0,称作纯自回归模型,记为AR( p);若p=q=0,模型退化为Xt=at,即{Xt}为白噪声序列。
2.2 基于ARMA(p,q)模型对零偏数据建模
根据实验室数据采集装置采集的零偏数据和时间序列建模的方法,对零偏数据时间序列进行ARMA(p,q)建模[8]。建模具体流程如图2所示。

图2 零偏数据时间序列模型建模流程图Fig.2 Modeling process of time series model of zero offset data
图2中,ACF为自相关系数,PACF为偏自相关系数。
2.2.1 时间序列数据的平稳性检验
时间序列的平稳性是建模的重要前提。检验时间序列的平稳性必须考虑以下两个内容:一是序列的均值和方差是否为常数;二是序列的自相关函数是否仅与时间间隔相关,而与此间隔端点位置无关。检验时间序列平稳性的常用两种方法是参数检验法和非参数检验法[9]。根据零偏数据时间序列样本个数较小的特点,本文采用非参数检验法(即游程检验)。对真实数据进行非参数检验,可知|Z|=4.43>1.96,所以原始零偏数据是非平稳时间序列。对真实数据进行一次差分得到一阶差分数据,再对一阶差分数据进行非参数检验,可知|Z|=1.34<1.96,所以一阶差分数据平稳。真实数据和一阶差分数据的非参数检验值如表2所示。
2.2.2 基于AIC准则模型定阶
本文采用Akaike信息准则对模型定阶[10],该准则由H.Akaike给出,其定义为:
AIC准则的思想是:在p、q的有效范围内寻求使得统计量A( s)达到最小的点,并将其做为(p,q)阶数的估计。通过Matlab数据分析软件,分别计算一阶差分后数据的自相关系数(ACF)和偏自相关系数(PACF),并得到相应数据图,如图3所示。
由图3可知,自相关系数(ACF)和偏自相关系数(PACF)都具有拖尾性。因此,选择ARMA(p,q)模型,确定参数的范围为0≤p≤6、0≤q≤19。根据式(3)计算AIC的值,通过计算得到AIC的最小值为2.35,此时对应的p=6、q=16。因此得到的时间序列模型为ARMA(6,16)。
2.2.3 基于最小二乘法模型的参数估计
选择合适的拟合模型之后,利用序列的观察值确定该模型中未知参数的值。常用的对未知参数的估计方法有3种:矩估计、极大似然估计和最小二乘估计[7]。结合参数模型,本文选用工程上最常用的参数估计方法,即最小二乘估计法。
为了获得满足ARMA(p,q)模型在时间序列相邻的n个观测值x1,x2,…,xn,有逆转形式:

在式(4)中取t=1,2,…,n,得误差平方和为:

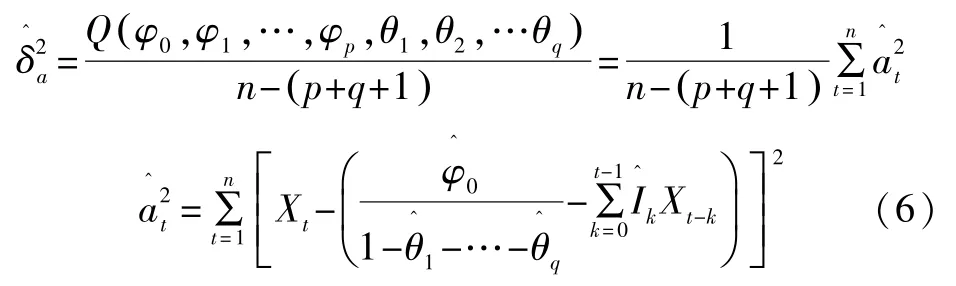
结合最小二乘法原理及式(4)、式(6),Matlab估计出的各个参数值如表3所示。
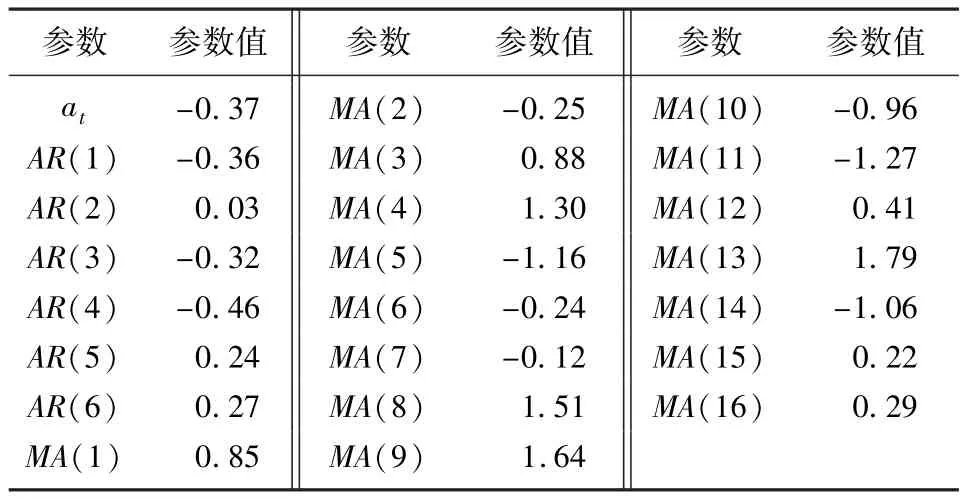
表3 模型参数通过最小二乘法估计的参数值Tab.3 The model parameter values estimated by the least squares method
2.2.4 模型显著性检验
模型显著性检验[8]主要是检验模型的有效性。一个模型是否显著有效主要是看它提取的信息是否充分,即残差序列应为白噪声序列。原假设和备择假设分别为:
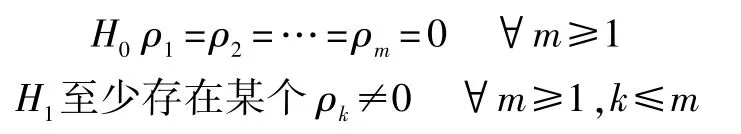
检验统计量LB:

如果拒绝原假设,说明残差序列中还残留着显著相关信息,拟合模型不显著;如果不能拒绝原假设,则则认为拟合模型显著有效。
为了便于分析,本文采用Eviews软件分析分析时间序列模型的残差是否为白噪声。经过Eviews软件分析得到原一阶差分数据的残差数据如图4(a)所示;对残差数据进行相关性分析后,得到的P值如图4(b)所示。由图4(b)可知,残差P均大于界限值0.05,所建模型接受假定参数取值,所以模型是有效的。
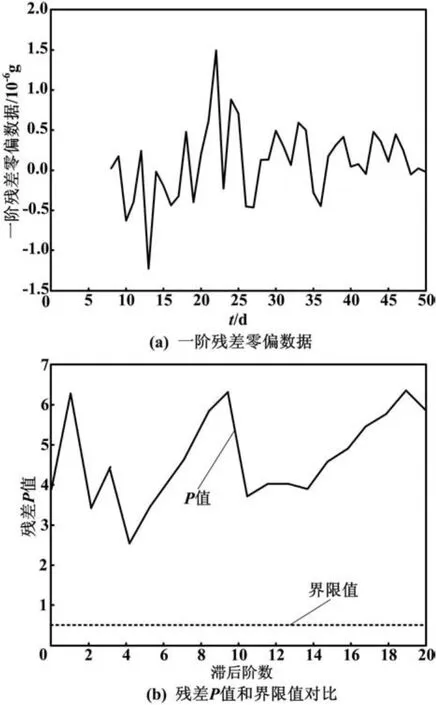
图4 一阶差分数据的残差分析图Fig.4 The residual analysis of the first-order differential data
2.2.5 模型预测
经过对零偏数据规律和特点的分析,建立的时间序列模型为:ARMA(6,16)。采用该模型对零偏数据进行预测,并进行还原差分,拟合真实数据和预测数据如图5所示。真实数据和预测数据[7]从第410 d到第500 d的误差分析如表4所示。
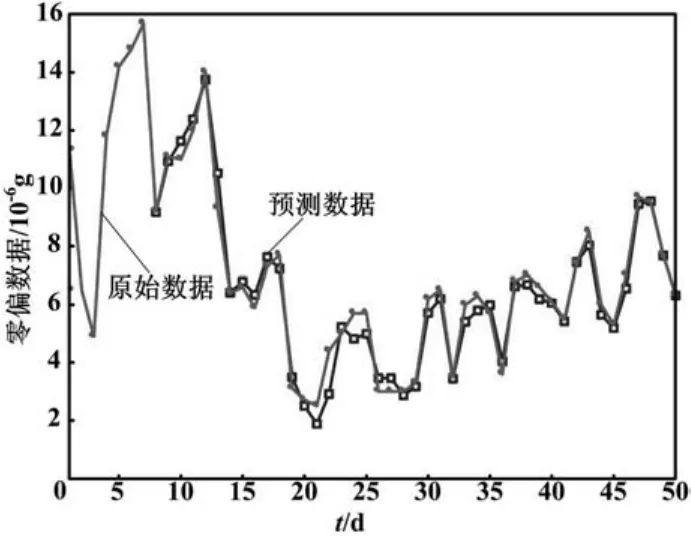
图5 真实数据和预测数据对比图Fig.5 Comparison of real data and forecasting data
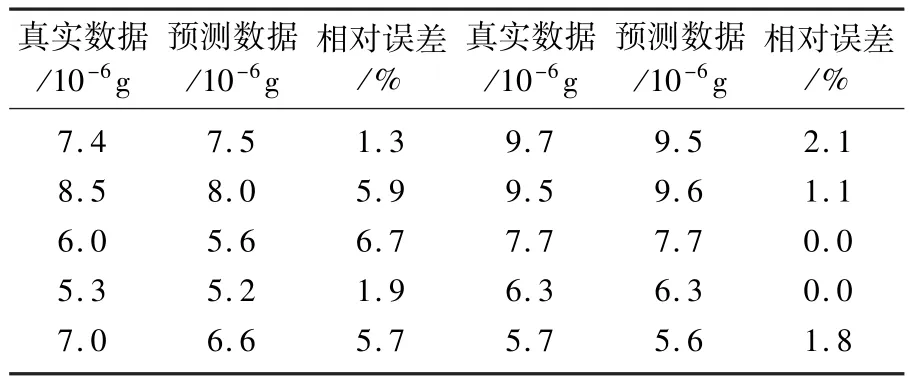
表4 真实数据和预测数据相对误差分析Tab.4 The relative error analysis of real data and forecasting data
由图5和表4可知,石英挠性加速度计零偏数据建立时间序列模型的预测数据和真实数据相对误差均在10%以内,证明了建模的有效性。
3 结束语
在贮存条件下,石英挠性加速度计零偏数据会随着周围环境发生随机性变化。本文采用石英挠性加速度计数据采集装置采集零偏数据,分析零偏数据随周围环境变化的规律和特点,得到相应时间序列,建立基于ARMA(p,q)模型的零偏数据时间序列模型。通过模型仿真,得到石英挠性加速度计零偏数据的预测值,分析预测结果可知,预测数据和真实数据误差均在接受范围内。通过对比和分析贮存条件下石英挠性加速计真实数据和预测数据,得到石英挠性加速度计在贮存条件下的稳定性变化规律,为研究石英挠性加速度计零偏数据提供了理论依据。
[1] Cheng Hongjie,Zhao Yuan,Qian Zhibo.Research on performance analyzing and modeling of quart flexible accelerometer[J].Electronic Measurement&Instruments,2009(8):412-415.
[2] 王珂.石英扰性加速度计偏值和标度因数稳定性的研究[D].哈尔滨:哈尔滨工程大学,2012.
[3] 许丹,廖寻,陈云霞,等.加速度计贮存稳定期分析[J].北京航空航天大学学报,2013,39(2):173-174.
[4] 唐永超,冯志刚,田军,等.石英挠性加速度计热固耦合仿真分析[J].强度与环境,2012,39(6):53-54.
[5] 张鹏飞,龙兴武.石英挠性加速度计误差补偿模型的研究[J].传感技术学报,2006,19(4):1100-1101.
[6] 韩瑞玲,佟连军,朱绍华,等.基于ARMA模型的沈阳经济区经济与环境协调发展研究[J].地理科学,2013(11):56-57.
[7] Ives A R,Abbott K C,Ziebarth.alysis of ecological time series with ARMA(p,q)models[J].The Ecological Society of America,2010, 91(3):858-859.
[8] 王燕.应用时间序列分析[M].北京:中国人民大学出版社, 2005:16-106.
[9] 张树京,齐立心.时间序列分析简明教程[M].北京:清华大学出版社,2003:1-117.
[10] 卢艳超,温卫宁,赵彪,等.基于EEMD-ARMA模型的电网工程导线价格预测[J].电力建设,2013,34(11):39-41.
Analyzing and Modeling Method for the Zero Offset of Quartz Flexible Accelerometer
Aiming at the problem that the parameter drift of quart flexible accelerometer will be influenced by the factors,i.e.,temperature, vibration and humidity,the stability of quartz flexible accelerometer under storage condition is studied.Firstly,the zero offset data of quartz flexible accelerometer under storage condition are collected,and the characteristics and rules of data are analyzed;then the time series mathematical model is established;finally the simulation of the model is conducted.The real data and the predicted data under storage condition are compared,the result of comparison shows that the modeling is effective;the relative errors of data obtained by modeling are within the range of tolerance,thus the applicability of modeling is verified.The predicted data reflect the regular pattern of zero offset following the changes of surrounding environment under storage condition;this provides theoretical reference for researching the stability of quartz flexible accelerometer under storage condition.
Time series model Quart flexible accelerometer Zero offset data Autoregressive and moving average mode Data analysis
TP212+.1
A
国防基金资助项目(编号:12ZG6103)。
修改稿收到日期:2014-04-29。
王洪(1988-),男,现为西南科技大学控制理论与控制工程专业在读硕士研究生;主要从事传感器技术、机器人控制技术的研究。
