基于双树复小波变换的转静碰摩响应分析
2014-05-25李纪永李舜酩陈晓红江星星
李纪永,李舜酩,陈晓红,江星星
(1.南京航空航天大学能源与动力学院,南京 210016;2.南京航空航天大学理学院,南京 210016)
基于双树复小波变换的转静碰摩响应分析
李纪永1,李舜酩1,陈晓红2,江星星1
(1.南京航空航天大学能源与动力学院,南京 210016;2.南京航空航天大学理学院,南京 210016)
针对碰摩故障诊断中转静碰摩响应消噪及特征提取构造分段圆弧平滑阈值函数,利用小波、小波包及双树复小波(Dual-tree Complex Wavelet)分别对非平稳信号降噪处理,以信噪比为指标判断降噪效果。结果表明,构造的阈值函数消噪具有高效性。通过计算单转子局部碰摩动态响应,用双树复小波对位移响应进行特征提取。与小波及小波包相比,双树实小波近似解析性及采样插值具有互补特点,能完整提取动态响应特征,减少信息丢失。并用仿真及转子碰摩实验验证该方法的有效性。
转静碰摩;降噪;动态响应;阈值函数;双树复小波
航空发动机中转静碰摩有两类,即转动部分碰摩部位不在转轴本身如叶片等与静止部分发生的碰摩及转动部分发生在转轴本身的碰摩。碰摩故障通常表现为其它故障的间接结果[1-2],如转子质量不平衡、热弯曲、轴系不对中及转子涡动失稳等均可能表现为转静碰摩。碰摩发生时一般为先有局部碰摩,即在一个周期内转子与定子发生一次或数次碰撞。冲击产生接触力及摩擦力,摩擦力将转子转动能量转化为横向振动同时伴有较复杂的振动现象,在某些条件下会出现混沌运动。
通过小波及小波包分析碰摩非平稳信号[3-4]可提取细节成分,但仍有3种缺陷限制其应用[5]:①平移敏感性,即输人信号平移会在小波分解系数中产生不可预计变化;②方向性差,只能提供3个空间方位;③相位信息缺乏。小波变换域的能量越集中说明小波分析效果越好,而该能量集中程度与小波幅频、相频特性有关。小波滤波器非理想截止特性及分解过程隔点采样会致信号分解、重构时产生虚假频率成分。
双树复小波变换(Dual-tree Complex Wavelet Transform,DTCWT)由Kingsbury[6]提出。Salesnick等[7]对双树复小波滤波器构造进行深入研究。双树复小波变换具有的良好抗频带混叠能力及平移不变特性可保证双树复小波变换在滤波器特性及周期复合冲击特征检测方面优于经典离散小波变换、第二代小波变换及经验模式分解等时频域分析方法。
降噪可视为经典的非参数回归,现有函数估计方法包括样条曲线拟合估计、核函数估计及傅里叶展开估计等[8]。Donolo等[9-10]在小波变换基础上提出的阈值降噪方法优势在于小波基函数空间多样性。小波变换稀疏性及去相关性保证真实信号小波变换能量集中于有限的小波系数,而如何选取阈值及阈值函数为实现小波去噪算法中关键问题[11]。阈值计算方法[12]有:stein无偏估计、固定阈值及启发式阈值;阈值函数有硬阈值、软阈值。硬阈值含间断点造成重构信号振荡,重构信号不光滑;软阈值所得小波系数与原小波系数存在固定偏差,影响重构信号逼近程度。为此,研究者构建不同阈值函数,包括折衷阈值函数、指数阈值函数等,但大多与真实小波系数有一定偏差。
本文采用stein无偏估计计算阈值,利用构造的阈值函数对双树复小波变换后非平稳信号进行降噪处理,计算单转子碰摩响应,并对碰摩位移响应用双树复小波进行特征提取;利用单转子及多转子碰摩实验验证本文所提方法。
1 双树复小波分解
DTCWT由两实值小波φh(t)与φg(t)构成复小波,即

式中:φg(t)=H[φh(t)],H为Hilbert算子。
两正交小波函数组成Hilbert变换对的充要条件[5]为两低通滤波器满足半采样延迟条件。其幅值与相位存在关系为
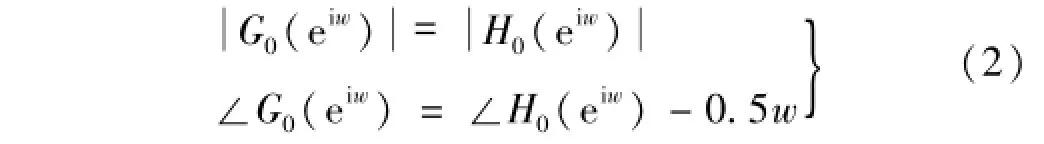
构造关键环节为使两小波函数滤波器满足式(2),构造方法有线性正交法、共同因子法及Q平移方法(quarter shift)。Q平移法设计的滤波器为

式(3)精确满足幅值条件,近似满足相位条件,其相位表达式为

对称中心在点n=0.5(N-1)-0.25附近。利用Q平移方法设计的双树复小波变换整体为精确线性相位,由于φc(t)的解析性,DTCWT具有近似平移不变与抗频带混叠等优良特性。前者有益于多重谐波信号检测;后者对提取周期性冲击特征非常有利。
2 双树复小波降噪阈值及阈值函数
利用小波降噪核心为阈值及阈值函数选择。含噪信号表示为:s=f+se,e为服从标准正态分布的高斯白噪声,其强度可用稳健估计方法计算,即σ=中值运算利用stein无偏似然估计,将某次层系数平方按由小到大排列,获得某向量W=[w1,w2,…,wn],其中w1≤…wn,n为小波系数个数。由此估算向量R=[r1,r2,…,rn],其中:

式中:0≤α≤1,不同a值对应不同阈值函数,实用性强,缺点亦明显,即具有间断点且与真实系数有一定偏差。
为克服软、硬阈值缺点,构造分段圆弧平滑阈值函数,设圆1半径r1,圆2半径r2,几何关系见图1。由图1看出,圆弧1半径为r1,圆弧2半径为r2,圆1圆心坐标为O1(1-r1,r1),圆2圆心坐标为O2(1+r2,r1),半径满足几何关系r1+r2=βt。其中0≤β≤1。

图1 几何关系示意图Fig.1 Geometric relation schematic
分段圆弧平滑阈值函数可表示为
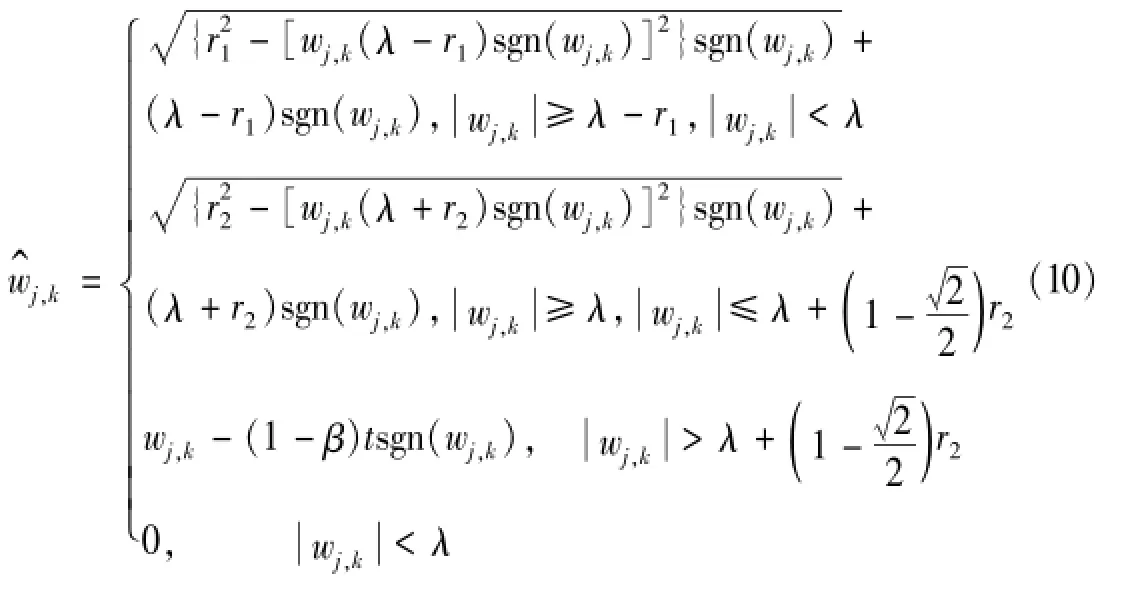
改进的阈值函数在各点处一阶可导,利于数学处理,避免信号重构时出现振荡。调节参数b及半径r1即可得不同折衷阈值函数。b=1时即可平滑过渡至真实小波系数。a=0.5,b=1时示意见图2。
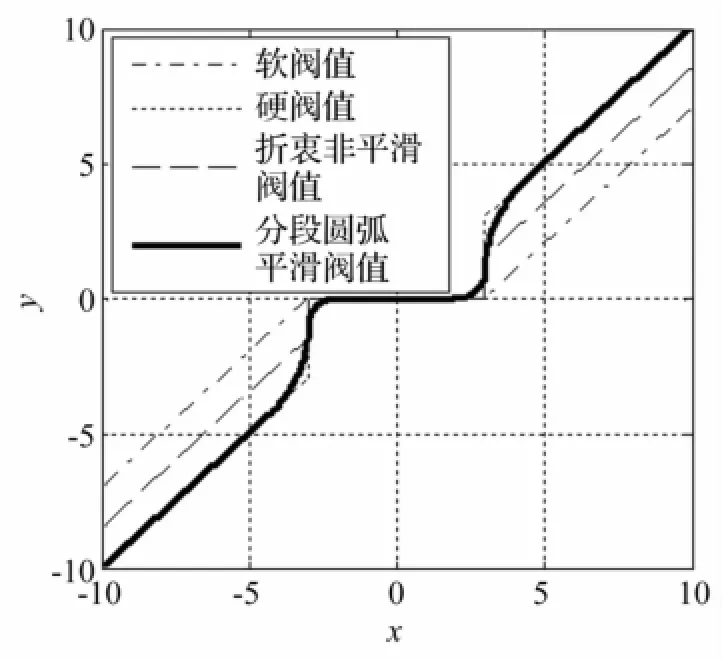
图2 阈值函数Fig.2 Threshold function
利用典型非平稳信号Heavy sine(初始信噪比6.4 dB)、Doppler(初始信噪比6.4 dB)、Bump(初始信噪比7.3 dB)、Blocks(初始信噪比9.6 dB)验证分段圆弧平滑阈值函数降噪的有效性。信噪比依次(每组SNR顺序从左至右,先第一行后第二行)见表1。综合比较可知,双树复小波去噪性能较好,从而验证分段光滑圆弧平滑阈值函数降噪的有效性。
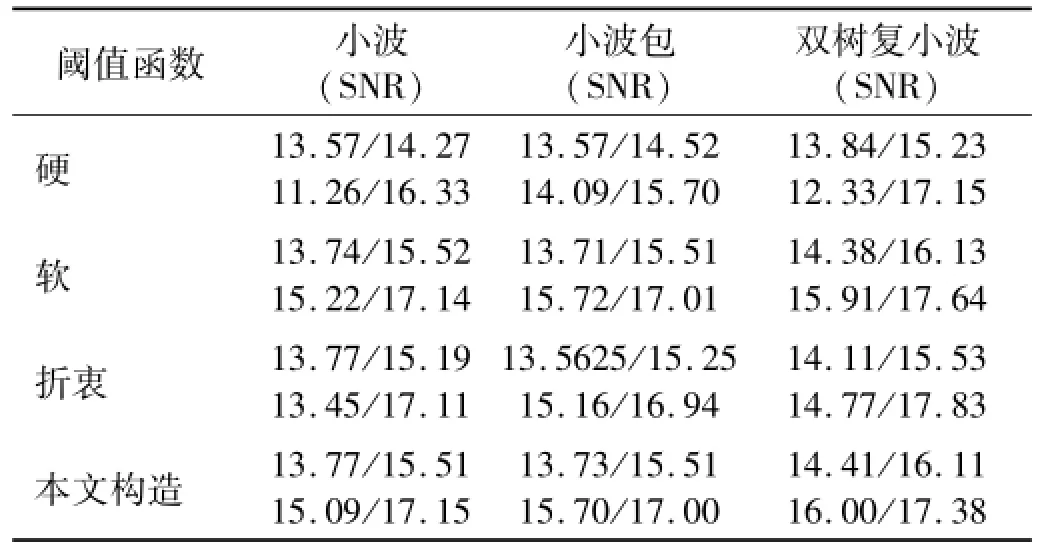
表1 Heavy sine,Doppler,Bump,Blocks降噪后SNR值Tab.1 SNR of denoised Heavy sine Dopp ler,Bum p,Blocks
3 单转子仿真碰摩响应双树复小波分析
Jeffcott单转子碰摩模型见文献[2],本文重设参数为
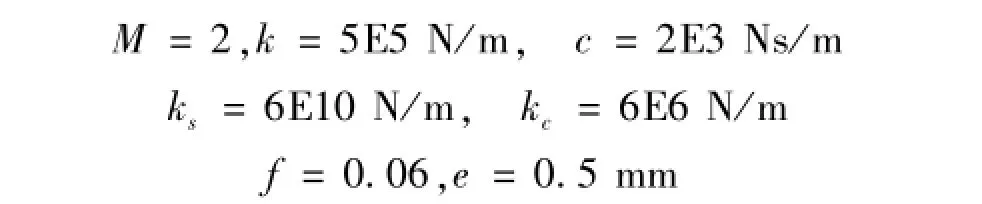
式中:M为转子质量;c为轴阻尼;k为轴刚度;ks为非线性刚度系数;f为摩擦系数;kc为定子径向刚度。
计算转子动态位移响应其分叉图见图3。令s=ω/ωc,ωc为临界转速。分析s=5.65时动态响应,利用Wolf方法求得lyapunov指数为0.022,时间历程及庞加莱映射见图4(a),响应呈非线性;其频谱见图4(b),存在的高频率成分未完全显示,如s=84、95.2、112,所取信号频率成份较丰富,能较好反映转子碰摩故障现象。
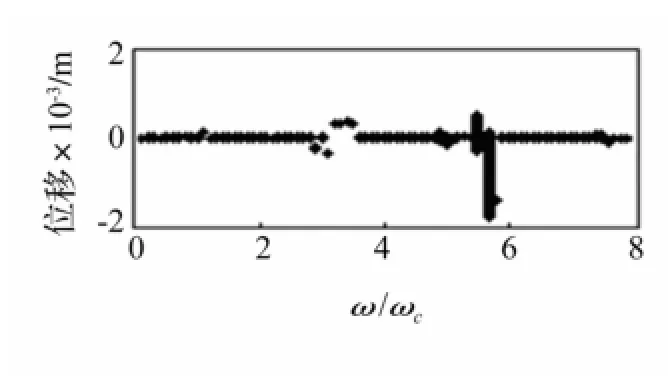
图3 转子系统分叉特性Fig.3 Rotor system bifurcation characteristic

图4 混沌信号时域及频域特征Fig.4 Chaos response time and frequency characteristic

图5 不同分解方法所得频谱Fig.5 Spectrum via different extraction methods
利用小波、小波包及双树复小波对混沌信号进行分析,所得频谱见图5。由图5(a)看出,小波分解各层存在严重频谱泄漏;而图5(b)中除频谱泄漏外亦存在较严重频率混叠,如第2层存在5个虚假频率,第3层节点在高频处存在虚假频率,第4层在中高频处存在虚假频率,小波及小波包分解的频率泄漏由滤波器非理想截止特性造成,小波包分解产生的虚假频率由分解过程中下抽样造成采样率降低,从而导致频率折叠及在重构过程中隔点插零操作形成。由图5(c)看出,第2层提取的响应高频成份包括s=84,95.2,112,得益于波重构过程中双树分解系数互补,减小信息丢失。各层几乎不存在虚假频率。此因双树复小波带通频率响应只在正半频率轴上(除第一层外),能减小频率混叠。而由于滤波器非理想截止特性,第4层存在频谱泄漏。
4 转子实验故障信号双树复小波分析
选单转子及三转子碰摩位移响应信号进行分析,其中三转子实验装置示意图见图6。单转子临界转速4 216 r/min、2 754 r/min时的碰摩位移及频谱见图7。由图7看出,基频45.9 Hz及2倍频91.8 Hz清晰可辨,而若干高次倍频成份淹没在噪声中。利用双树复小波进行降噪处理,选构造分段光滑阈值函数对信号重构,频谱见图8。由图8看出,已提取信号的高频细节信息,其中第二层含505.1 Hz,593.2 Hz,643 Hz等;第三层含328.3 Hz(7倍频),367.4 Hz等;第四层含183.8 Hz(4倍频),204.1 Hz;第5层为2倍频,频带间有轻微混叠,与相同分解层下小波包分解混叠频谱成份相比(图9,线框内),频率混叠成份大幅降低。
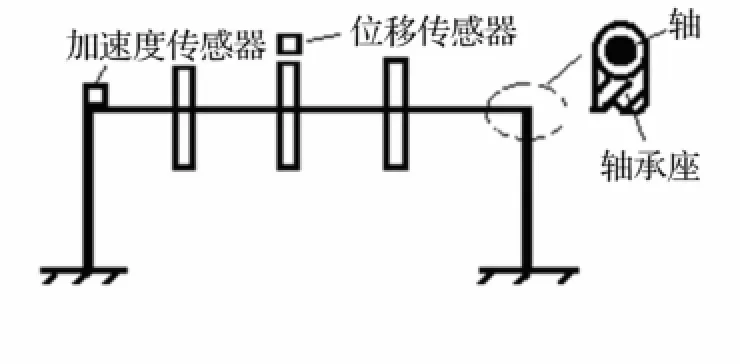
图6 转子装置示意图Fig.6 Rotor unit schematic

图7 转子位移响应时间历程及频谱Fig.7 Rotor displacement time history and its spectrum

图8 位移频谱Fig.8 Displacement spectrum

图9 位移频谱Fig.9 Displacement spectrum
三转子临界转速为1 867 r/min、转速为5 700 r/min时转子振动较大,轴与轴套发生碰摩。位移传感器测得碰摩信号及频谱见图10,除基频95.8 Hz外,亦产生2倍频及若干高次倍频。

图10 转子位移响应时间历程及其频谱Fig.10 Rotor displacement time history and its spectrum
利用双树复小波进行降噪处理,选构造分段光滑阈值函数对信号重构所得频谱见图11,已提取信号的高频细节信息,其中第二层含669.5 Hz,765.3 Hz,860 Hz,分别为7、8、9倍频;第三层含382 Hz,为4倍频;第四层含191.2 Hz,为2倍频。各频带间无混叠,有用信息获得充分显示。

图11 位移频谱Fig.11 Disp lacement spectrum
5 结 论
(1)构造的分段圆弧平滑阈值函数在整个区间一阶导数连续,能避免重构信号振荡,可有效消除非平稳信号中噪声。
(2)利用双树复小波变换分析碰摩非线性动态响应信号提取的转子动态响应高频信号与小波及小波包变换相比,双树复小波变换能抑制模式混叠,并能提取更多细节信息。
(3)由两平行但不同的离散小波组成的双树复小波变换其双树分解系数信息互补,可减少由下采样造成的信息丢失,能完整提取碰摩故障信号特征;其双树实小波解析特性可抗频带混叠并具有平移不变特性,减少信号信息特征丢失,在故碰摩故障信号特征提取中效果较好。
[1]Han Q,Zhang Z,Wen B.Periodic motions of a dual-disc rotor system with rub-impact at fixed limiter[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2008,222(10):1935-1946.
[2]Chu F,Zhang Z.Bifurcation and chaos in a rub-impact Jeffcott rotor system[J].Journal of Sound and Vibration,1998,210(1):1-18.
[3]Lin J,Qu L.Feature extraction based on Morletwavelet and its application for mechanical fault diagnosis[J].Journal of Sound and Vibration,2000,234(1):135-148.
[4]Peng Z,He Y,Lu Q,et al.Feature extraction of the rubimpact rotor system by means of wavelet analysis[J].Journal of Sound and Vibration,2003,259(4):1000-1010.
[5]Kingsbury N.Complex wavelets for shift invariant analysis and filtering of signals[J].Applied and Computational Harmonic Analysis,2001,10(3):234-253.
[6]Selesnick IW,Baraniuk R G,Kingsbury N C.The dualtree complex wavelet transform[J].Signal Processing Magazine,2005,22(6):123-151.
[7]Selesnick IW,Baraniuk R G,Kingsbury N C.The dual-tree complex wavelet transform[J].Signal Processing Magazine,IEEE,2005,22(6):123-151.
[8]Chang SG,Yu B,VetterliM.Adaptivewavelet thresholding for image denoising and compression[J].Image Processing,IEEE Transactions on,2000,9(9):1532-1546.
[9]Donoho D L.De-noising by soft-thresholding[J].Information Theory,IEEE Transactions on,1995,41(3):613-627.
[10]Donoho D L,Johnstone I M.Adapting to unknown smoothness via wavelet shrinkage[J].Journal of the American Statistical Association,1995,432(90):1200-1224.
[11]吴定海,张培林,任国全,等.基于双树复小波包的发动机振动信号特征提取研究[J].振动与冲击,2010,29(4):160-163.
WU Ding-hai,ZHANG Pei-lin,REN Guo-quan,et al.Feature extraction of an engine vibration signal based on dualtree wavelet package transformation[J].Journal of Vibration and Shock,2010,29(4):160-163.
[12]Stein C M.Estimation of themean of a multivariate normal distribution[J].The Annals of Statistics,1981,9(6):1135-1151.
Rotor-stator rub-impact response analysis based on DTCWT
LI Ji-yong1,LIShun-ming1,CHEN Xiao-hong2,WANG Xing-xing1
(1.College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.College of Science,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China))
The de-noising of rub-impact response signals of a rotor-stator system and its characteristics extraction are key problems of rub fault diagnosis.A piecewise smooth threshold function was constructed forwavelet de-noising,and non-stationary signals were de-noised separately by using Wavelet,Wavelet packets and dual-tree complex wavelet transform(DTCWT).SNR(signal to noise ratio)was taken as an index to evaluate the de-noising effect.The results reveal that the constructed threshold function is highly active in de-noising.As an example,the dynamic response of a single rotor under rub-impactwas calculated and decomposed by DTCWT.The simulation and experiment results show that the dynamic response can be exactly derived due to the complementary property between approximate analyticity and sampling interpolation of DTCWT.It is also proved that the proposedmethod is effective.
rotor-stator rub;de-noising;dynamic response;threshold function;DTCWT
V233.1
:A
10.13465/j.cnki.jvs.2014.22.019
航空自然科学基金(2012ZD52054);国家自然科学基金项目(61403193);南航基本科研业务费科研项目(NS2014081)
2013-07-24 修改稿收到日期:2013-11-21
李纪永男,博士生,1984年生
李舜酩男,教授,1962年生邮箱:smli@nuaa.com
