响应传导函数在船舶机械噪声预报中的应用及实验验证

周军伟，何 琳，徐荣武，崔立林

（1．海军工程大学振动与噪声研究所，武汉 430033；2．海军工程大学船舶振动噪声重点实验室，武汉 430033）

响应传导函数在船舶机械噪声预报中的应用及实验验证

周军伟1，2，何 琳1，2，徐荣武1，2，崔立林1，2

（1．海军工程大学振动与噪声研究所，武汉 430033；2．海军工程大学船舶振动噪声重点实验室，武汉 430033）

据线性时不变系统自身具备的响应传导特性，将力－响应传递函数模型转化为响应－响应传导函数模型用于船舶机械噪声预报。理论推导传导函数法用于响应预报的约束条件，分析其用于船舶机械噪声实时预报的可行性。给出传导函数的求解方法－工况联合法，并对其应用条件进行分析论证。双层圆柱壳体模型试验结果表明，传导函数法用于近、远场机械噪声预报时均具有较高精确度。

机械噪声；实时预报；频响函数；传导函数；激励源；工况联合

对船舶辐射噪声的主要成分－机械噪声进行测量、评估意义重大［1］。水下结构辐射声的计算方法已有诸多研究［2－5］。该方法按原理可分三类，即解析法［3，6］、数值法［3，6］及实验测量法［3，7］。由于船舶结构的复杂性，解析法及数值法用于辐射噪声评估受到一定限制，而实验测量法基于船舶真实结构响应所得远场辐射噪声结果则相对准确。

实验测量法中传递函数法应用通常有三步：①由人工激励试验获得传递函数，亦称频率响应函数（FRF）；②识别实际工况设备作用于结构的激励力；③将前两步所得传递函数与激励力相乘得远场辐射噪声。受测量手段及设备安装条件限制，实际工况激励力较难获得。针对传递函数法面临的激励力识别难题，考虑避开求解激励力而直接由激励力作用系统各点响应间的传递关系实现对系统未知响应的预报评估，将问题转化为在设备激励下求解系统近场参考点与远场目标点响应间传递关系。由于该传递关系在一定约束条件下保持不变，因而可据此传递关系与实测所得参考点响应对远场目标点响应实时预报。为将力与响应间传递关系（用H表示，称传递函数）与响应－响应间传递关系（用T表示）进行区分，称一定约束条件下系统响应间传递关系为传导函数，其辐射噪声计算方法则称传导函数法。

本文首先建立物理模型对传导函数原理说明、推导，获得传导函数保持不变需满足的系统约束条件，即本文方法的适用范围。再通过数学分析论证多工况联合法求解响应传导函数的可行性，给出传导函数法用于船舶机械噪声实时预报方案。并通过双层圆柱壳体模型试验检验传导函数法的应用效果。

1 传导函数T推导

系统在设备激励下的响应传导函数T由激励力与结构响应间传递函数H推导获得。本质上传递函数H为基于力与响应间因果关系，而传导函数T则在系统及激励条件下响应与响应间的共存关系，二者均为关于频率ω的函数［8］。为表达简洁，将力、加速度、声压均默认为频率ω的函数。

所建设备激励力作用的系统响应物理模型，见图1。用加速度代表响应，亦适用其它响应（如位移、声压等）［9－10］。将一组作用力FA施加于系统，其参考点加速度响应集合记为AK，目标点加速度响应集合记为AU，由于力、参考点、目标点数量均大于1，故FA，AK，AU均为列向量集合。

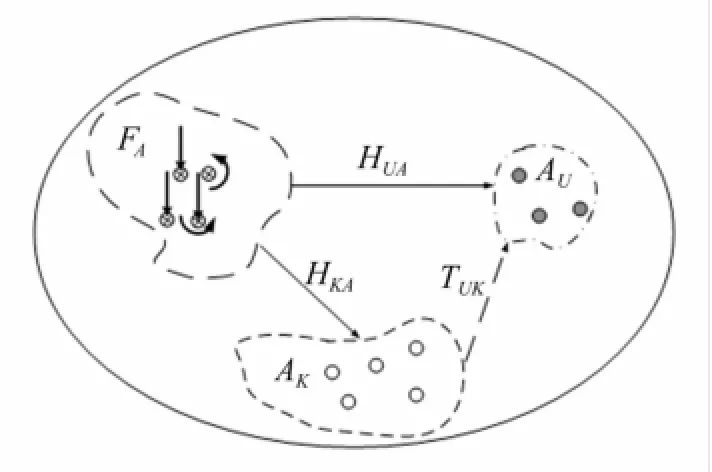
图1 系统受力响应模型Fig．1 System with force-response relationship

2 系统约束条件

由式（5）知，T由传递函数HUA及HKA的逆矩阵约束，使T保持不变需满足约束条件：①系统为线性时不变系统即满足响应叠加原理，传递函数能反映系统固有特性，不随激励力幅值变化［10－12］。②激励点、参考点、预报点三者数量及位置固定不变即满足矩阵HKA，HUA中元素数值不变。③参考点数量大于等于激励力数量即满足矩阵HKA的逆存在条件。

满足系统约束条件即能用试验所测响应传导函数结合实测参考点响应计算目标点的声响应。将设备激励的船舶与周围空间声传播介质作为研究系统（图示椭圆包围的区域），并近似为线性时不变系统，见图2。由于系统中各激励设备数量、位置均固定（用EA表示），只要选足够数量参考点（用XK表示），将其与目标点（用XU表示）位置固定，则两点响应间传导函数T保持不变。通过试验测得T，当船舶航行或停靠时无论处于何种设备激励组合，用布置船体的参考点XK响应数据与T联合计算即可求出目标点XU的声响应。

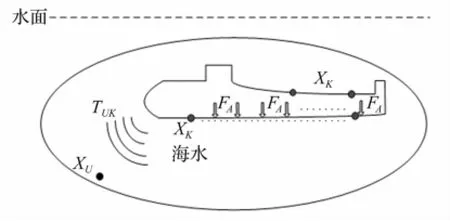
图2 设备激励下船舶噪声辐射模型Fig．2 Ship mechanical noisemodel with equipmentworking

3 工况联合法求解传导函数

3.1 原理分析

因分析知，传导函数T为频率ω的函数，见图3。对激励频率为ω0的作用力F（ω0），参考点与目标点响应的传导函数T也是关于频率ω0及倍频的函数，即T（ω0），T（2ω0），…；而对设备的宽带激励如激励频率为ω1－ω2，则亦可将宽带的传导函数T分解为T（ω1），T（ω1＋1），T（ω1＋2），…，T（ω2）进行逐个求解。

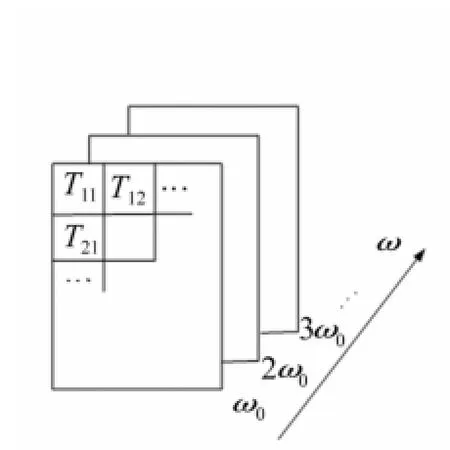
图3 传导函数频域属性Fig．3 Frequency dependency of TF

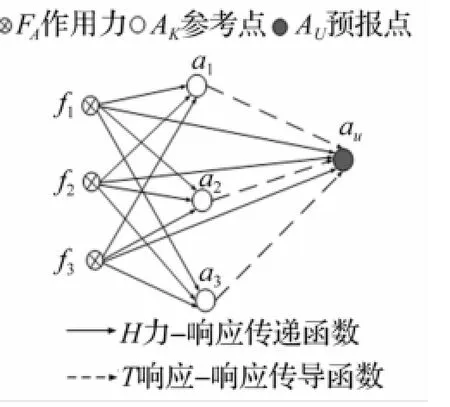
图4 力－响应及响应－响应关系模型Fig．4 Force-response vs．response-response

设三台设备的工作频率为ω0，其激励力幅值分别为f1，f2，f3；三参考点位置响应分别为a1，a2，a3；目标点响应为au，见图4。由响应－响应传导函数得

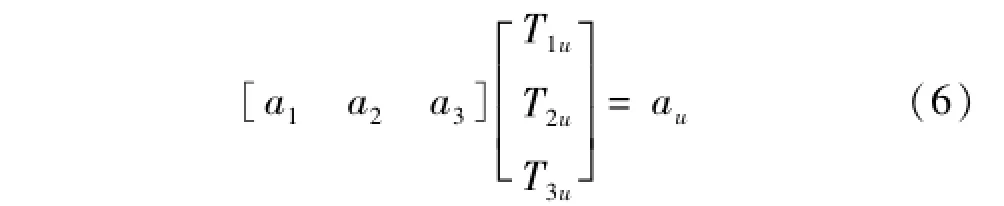
由于试验条件下式（6）中参考点响应［a1a2

a3］与目标点响应au均可通过传感器直接测得，但T1u，

T2u，T3u三未知数并不能由1个方程计算获得。据传导函数T保持不变时应满足的约束条件，可在约束条件下设计不同工况，记为m组。只要使每组工况各设备激励力幅值互不相同，即能连续获得一系列响应传导方程，即

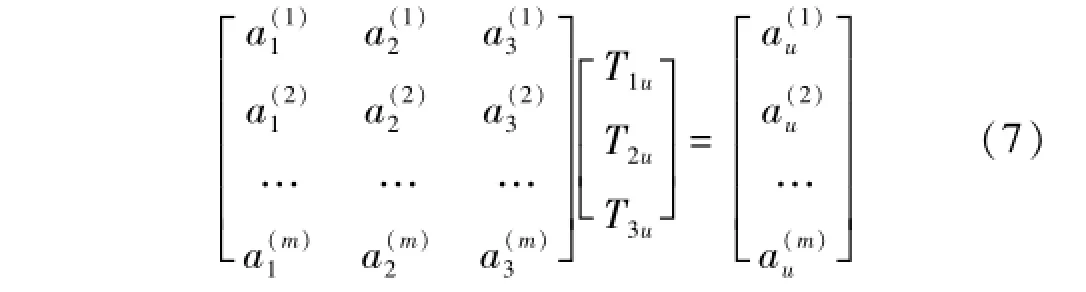
式中：上标（1）、（2）…（m）分别代表第1～m组工况所测响应。将式（7）变形，得传导函数T的解为

求解传导函数T需式（7）本身为适定或超定，即满足工况数m等于或大于参考点数k的条件。且对式（8）参考点响应矩阵AK的求逆运算尽可能精确，即矩阵AK趋于满秩，其行、列向量间保持线性无关。由式（9）看出，参考点响应由激励力与传递函数共同作用结果。不同工况的激励力幅值间相关性直接决定矩阵AK的行向量间相关性；传递函数矩阵各列之间相关性直接决定矩阵AK的列向量间相关性。因此，为获得参考点矩阵AK满秩结果，工况联合法求解传导函数T时应满足的约束条件为：①试验工况数大于或等于参考点数，即满足式（7）适定或超定。②不同工况的激励力幅值保持线性无关，即满足矩阵AK行向量间线性无关。③参考点应遵循分散、非对称布置原则，且应避开低频模态节点，即满足矩阵AK列向量间线性无关。

3.2 工况设置

求解某频率处传导函数时，为获得多组线性无关的激励力，可通过将工作在该频率的所有设备依次开启，或将设备遍历组合开启，或在保持设备同时开启情况下分别独立改变各设备激励幅值实现。以三台设备为例，工况设置方案分别对应于表1～表3。表中数字0代表设备关闭，1，2，3分别代表设备开启的各作用力相对幅值。

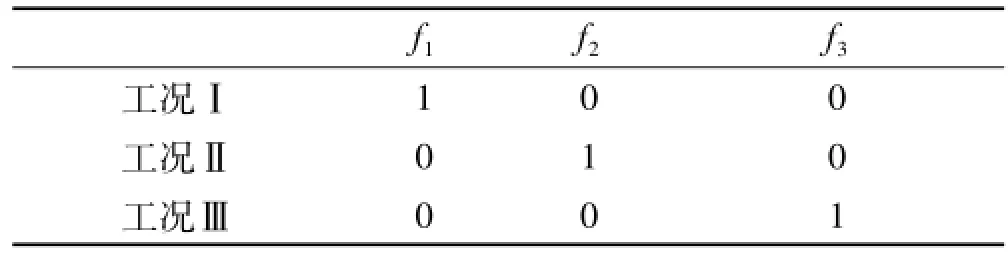
表1 依次独立开启Tab.1 Turn on separately in sequence

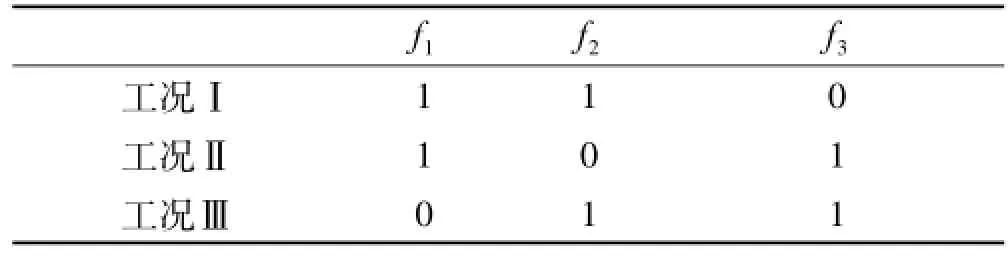
表2 遍历组合开启Tab.2 Turn on in combination and include all ones

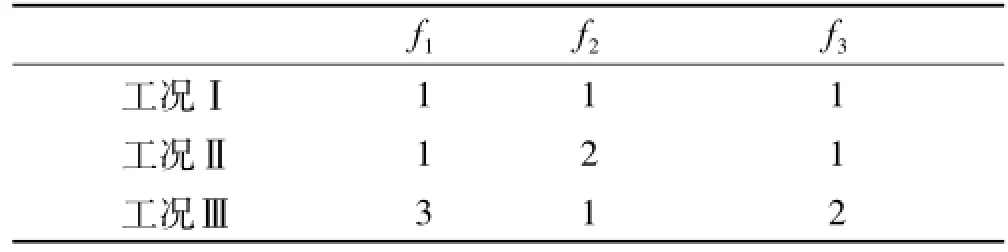
表3 同时开启独立变幅值Tab.3 Tu rn on sim ultaneously but vary individually

用以上工况设置方案可实现由较少试验工况数求得传导函数T，进而用于设备任意组合工况的远场响应评估，且该特性会随设备数量增多呈越显著优势。设在某频率处施加激励设备数量为10，则该10台设备对应的组合开启工况共N种，即

由式（10）求出N＝1 023。用工况联合法在试验中只需将10台设备分部开启建立10种线性无关工况即可求得传导函数T，可用于1023种工况的远场响应计算。

4 噪声预报实施流程

对传导函数T应用条件及求解方法论证分析后，给出传导函数用于船舶机械噪声实时预报的实施流程为：①将船舶机械设备按工作频率分组；②确定各工作频率下机械设备数量；③确定各工作频率下参考点数量及位置；④在远场目标位置布放水听器，开展多组线性无关的训练工况试验，通过所测得参考点及目标点响应求解各工作频率的传导函数存入数据库；⑤在船舶航行时据参考点实时响应数据由数据库中调取对应的传导函数，二者相乘获得船舶远场机械辐射噪声。

5 试验验证

5.1 近场结构响应预报

试验所用双层圆柱壳体模型外部尺寸及内部设备布置见图5、图6。为检验传导函数法用于响应预报的一般性，对模型在空气中外壳加速度响应进行预报验证。试验场所为半消声室，用于激励模型壳体的三台设备分别为电机、1＃激振器、2＃激振器。试验所用工况设置见表4，参考点及目标点位置见表5。

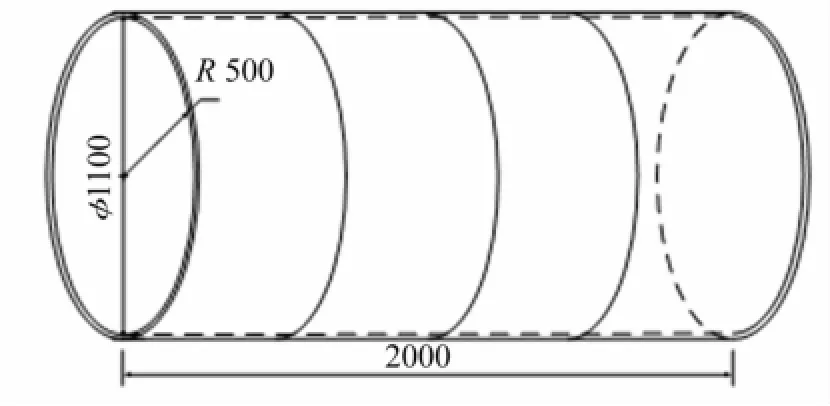
图5 双层圆柱壳体外形尺寸（单位：mm）Fig．5 External dimension of cylindrical double-shellmodel

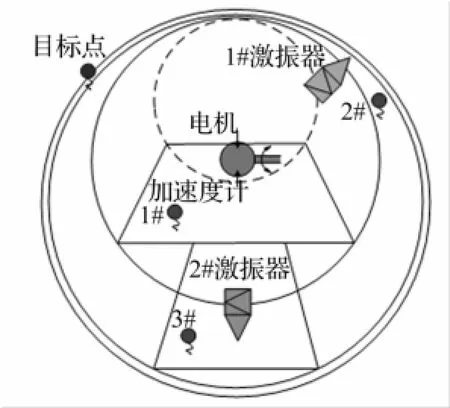
图6 圆柱壳体内部设备布Fig．6 Inner arrangement of cylindricalmodel

表4 陆上试验工况设置Tab.4 The training and validation conditions on land

表5 参考点及目标点位置Tab.5 The locations of reference and target points

由于三台设备激励频率不重合，理论上可只用1个参考点计算传导函数进行目标点响应预报。将参考点数量设为大于激励源数量。由式（8）据训练工况下所测参考点及目标点加速度响应求出传导函数T，将验证工况的参考点加速度与传导函数T相乘求得目标点预报响应，并将其与验证工况实测目标点响应进行比较，结果见图7。由图7看出，在设备激励频率处预报结果与实测值符合很好，各激励频率处预报误差分别为：61 Hz／2．45 dB；180 Hz／0．11 dB；300 Hz／0．56 dB。其它频率处因设备未进行有效激励，因而区域信号信噪比较低，预报结果意义不大。

5.2 水下辐射噪声评估

水下试验的消声水池见图8。双层圆柱壳体模型位于水下5 m，模型内安装3台激振器，在同深度距模型中心10 m处布设水听器，用于测量双层圆柱壳体远场辐射声压，同时作为辐射噪声评估的目标点。模型外壳分别布设20个加速度计及6个水听器用于近场参考点响应选取，试验中各激振器工况设置见表6，各工况参考点与远场目标点响应同测得。

表6 水下试验工况设置Tab.6 The training and validation conditions in underwater test

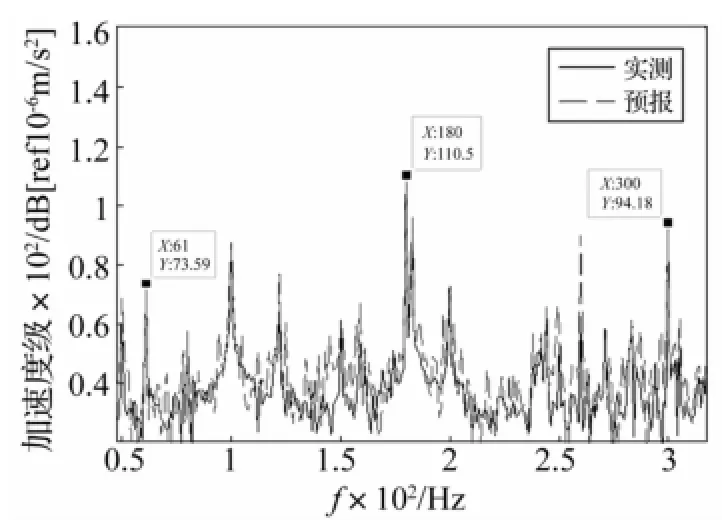
图7 结构加速度响应预报结果与实测值比较Fig．7 Comparison ofmeasured vs．estimated value on acceleration responses

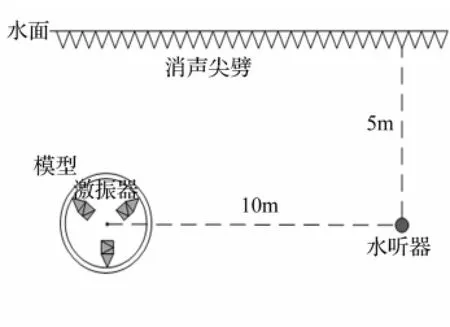
图8 双层圆柱壳体水下试验方位布置Fig．8 The arrangement diagram of underwater experiment

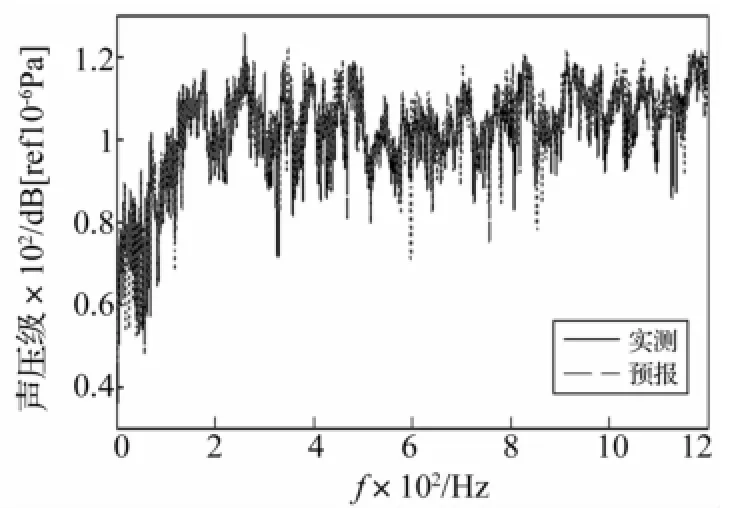
图9 外壳加速度作为参考点响应的预报结果（单频点）Fig．9 Comparison ofmeasured vs．estimated value using accelerometers measurement：single frequency point

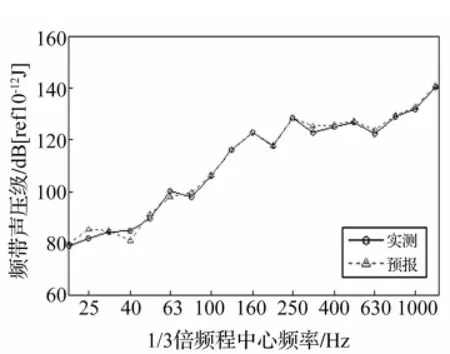
图10 外壳加速度作为参考点响应预报结果（1／3倍频程）Fig．10 Comparison ofmeasured vs．estimated value using accelerometers measurement：one-third octave

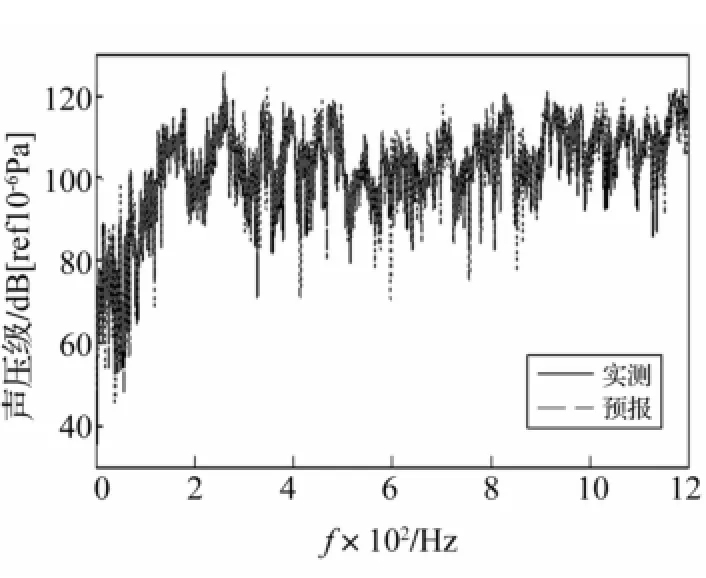
图11 外壳水听器作为参考点响应预报结果（单频点）Fig．11 Comparison ofmeasured vs．estimated value using hydrophones measurement：single frequency point

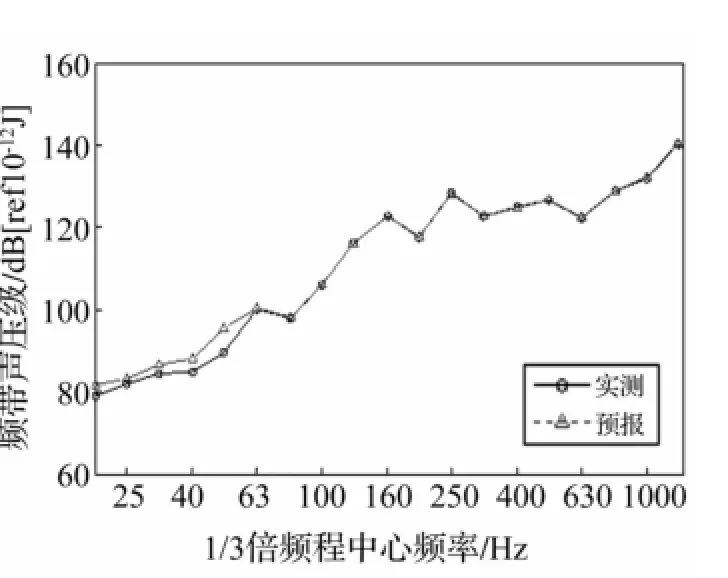
图12 外壳水听器作为参考点响应的预报结果（1／3倍频程）Fig．12 Comparison ofmeasured vs．estimated value using hydrophones measurement：one-third octave

用外壳加速度计作为参考点响应所得远场辐射声压预报值与实测值比较结果见图9、图10。用外壳水听器作为参考点响应所得远场辐射声压预报值与实测值比较结果见图11、图12。各试验结果分别以单频点及1／3倍频程形式表示。

5.3 试验结果分析

由双层圆柱壳体模型试验结果，可知：

（1）传导函数法用于响应预报精度较高。在中高频段（本试验模型对应150 Hz以上频段）的频带级预报误差小于2 dB，低频段（本试验模型150 Hz以下频段）的频带级预报误差小于5 dB，中高频段预报结果明显优于低频段。其原因可能为：①模型结构在低频区模态密度小，结构各参考点在单频点响应被有限模态主导，导致各频点参考点响应间相关性较高，使传导函数T计算结果不准确。随频率升高结构模态会越密集，每个频点均有较多模态对结构振动产生影响，各参考点响应间能保持互相独立，所求传导函数T精确度高，预报结果准确。由于模态密度与结构尺度关联，对如船舶大尺度结构，其模态密度对传导函数法预报结果影响尚需进一步研究。②低频段由于水中流固耦合影响，水在外壳体产生的等效附加质量较大，导致阻抗变大，结构不易被激励，导致所测响应信号信噪比差，影响计算及预报结果。

（2）1／3倍频程的预报结果优于单频点。由图9、图11看出，预报结果主要在响应极低的频率点（反共振频率）及响应极高的频率点（共振频率）处误差较大，由于反共振频率处信号信噪比低，共振频率处信号测量误差被放大，二者皆会导致预报误差变大。而用1／3倍频程处理预报结果时能在一定程度上抵消各频点处由测量随机误差导致的影响，使预报结果更准确。

（3）用外壳水听器的数据作为参考点响应所得预报结果优于用外壳加速度计数据。原因为考虑加速度计易受安装条件影响，当加速度计轴线偏离结构表面法向时会导致测量误差。

（4）由参考点位置选取对试验结果影响看出，参考点选取原则是成立的，即参考点位置尽量分散，非对称，避开低阶模态节点。

6 结 论

本文据线性时不变系统自身存在的响应传导特性，研究响应传导关系用于船舶机械噪声评估的可行性，通过理论推导得出传导函数法的应用约束条件。给出传导函数求解方法－工况联合法，并对工况联合法的应用条件进行分析论证。双层圆柱壳体模型试验表明，传导函数法预报结构响应及评估远场辐射噪声效果均较好。

［1］王之程，陈宗岐．舰船噪声测量与分析［M］．北京：国防工业出版社，2004：3－5．

［2］金广文．双层圆柱壳体水下噪声实时预报方法研究［D］．武汉：海军工程大学，2008．

［3］汤智胤．潜艇声隐身态势评估研究［D］．武汉：海军工程大学，2011．

［4］王斌．基于表面振动监测的大型水下结构辐射噪声预报研究［D］．上海：上海交通大学，2008．

［5］彭旭，骆东平．船舶结构建模及水下振动和辐射噪声预报［J］．噪声与振动控制，2003（6）：9－12．

PENG Xu，LUO Dong-ping．The modeling of the ship and numerical simulation of coupled vibro-acoustic behavior by FEM／BEM［J］．Noise and Vibration Control，2003（6）：9－12．

［6］孙雪荣，朱锡．船舶水下结构噪声的研究概况与趋势［J］．振动与冲击，2005，24（1）：106－113．

SUN Xue-rong，ZHU Xi．Status and trend of underwater noise research on ship structure［J］．Journal of Vibration and Shock，2005，24（1）：106－113．［7］何元安，杨德森．水下结构辐射噪声估算方法实验研究［J］．船舶力学，1999，3（2）：58－61．

HE Yuan-an，YANG De-sen．Experimental study on underwater structure radiated noise evaluation［J］．Journal of Ship Mechanics，1999，3（2）：58－61．

［8］Maia N M，Silva JM．The transmissibility concept in multidegree-of freedom systems［J］．Mechanical Systems and Signal Processing，2001，15（1）：129－137．

［9］张磊，曹跃云，杨自春，等．船舶噪声源的传递率矩阵识别方法及试验验证［J］．振动工程学报，2013，26（2）：291－297．

ZHANG Lei，CAO Yue-yun，Yang Zi-chun，et al．Transmissibility matrix method for identification of ship noise source and corresponding test verification［J］．Journal of Vibration Engineering，2013，26（2）：291－297．

［10］张磊，曹跃云，杨自春，等．双层圆柱壳体水下振动噪声结构传递路径分析［J］．振动与冲击，2012，31（20）：12－16．

ZHANG Lei，CAO Yue-yun，YANG Zi-chun，et al．Structural transfer path analysis for vibration and noise of a submerged cylindrical double-shell［J］．Journal of Vibration and Shock，2012，31（20）：12－16．

［11］傅志方，华宏星．模态分析理论与应用［M］．上海：上海交通大学出版社，2000：1－20．

［12］曹跃云，张磊，杨自春，等．船舶振动噪声源传递路径分析及试验验证［J］．振动与冲击，2013，32（22）：159－162．

CAO Yue-yun，ZHANG Lei，YANG Zi-chun，et al．A new OPA model for ship noise sources and test validation［J］．Journal of Vibration and Shock，2013，32（22）：159－162．

Practical app lication and experimental verification of transm issibility function in ship mechanical noise prediction

ZHOU Jun-wei1，2，HE Lin1，2，XU Rong-wu1，2，CUILi-lin1，2
（1．Institute of Noise＆vibration，Naval University of Engineering，Wuhan 430033，China；2．National Key Laboratory on ship Vibration＆Noise，Wuhan 430033，China）

The traditional response estimation model is based on force-response relationship．According to the transmissibility concept in linear time invariant system，a new response estimation method by the name of transmissibility function（TF）method was provided based on response-response relationship．The principle of themethod was interpreted in mathematic formula and the restriction condition was presented．Then，an engineering technique called operational conditions combination was presented for calculating the transmissibility function（TF）of vibration responses，and the guideline on how to devise the scheme of working conditions was discussed．The performance of the developed transmissibility function method was validated by a cylindrical double-shell vibration test．

mechanical noise；real-time prediction；frequency response function（FRF）；transmissibility function（TF）；exciting force；operational conditions combination

TB53

：A

10．13465／j．cnki．jvs．2014．22．014

国家自然科学基金（51209214）；国防科技重点实验室基金（SYSZC2012006）

2013－08－15 修改稿收到日期：2013－11－28

周军伟男，博士生，1983年生

徐荣武男，博士，副研究员，1980年生