基于秩相关随机变量模拟的水库防洪风险估计*

程 亮，王宗志，金菊良，刘克琳，吴成国

（1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏南京210029；2.合肥工业大学土木与水利工程学院，安徽合肥230009；3.合肥工业大学水资源与环境系统工程研究所，安徽合肥230009）

基于秩相关随机变量模拟的水库防洪风险估计*

程 亮1，王宗志1，金菊良2，3，刘克琳1，吴成国2，3

（1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏南京210029；2.合肥工业大学土木与水利工程学院，安徽合肥230009；3.合肥工业大学水资源与环境系统工程研究所，安徽合肥230009）

采用基于Spearman秩相关随机变量模拟方法，将拉丁抽样法产生的独立洪峰洪量序列转换成满足特定相关结构的洪峰洪量序列，利用模拟的洪峰和时段洪量放大修匀典型过程线生成入库洪水过程，实现了入库洪水过程随机模拟。采用Monte Carlo法估计防洪风险，构建了水库防洪风险估计模型。潘家口水库汛限水位调整防洪风险估计应用结果表明：主汛期汛限水位上限值控制在218.00 m，所建立的入库洪水过程模拟方法简便有效，非常适合于复杂洪水过程模拟，构建的防洪风险分析模型计算结果客观合理，在洪水资源安全利用系统风险分析中具有推广应用价值。

水库防洪风险估计；洪水资源利用；分期汛限水位；秩相关随机变量；洪水模拟

对汛期进行分期，采用分期汛限水位能有效缓解防洪与兴利的矛盾，是水库洪水资源利用的有效途径之一［1］。在带来兴利效益的同时，汛限水位调整也可能影响水库防洪安全。合理估计汛限水位调整的防洪风险是分期汛限水位综合论证重要工作内容之一［2］。水库防洪风险分析方法有频率分析法、均值一次二阶矩法及其改进、JC法、随机微分方程法和Monte Carlo法等［3］。Monte Carlo法作为一种通用性很强的风险分析方法被广泛用于防洪风险分析［4－10］。利用Monte Carlo法计算水库防洪风险率的关键是模拟生成入库洪水过程。常用的洪水过程随机模拟模型有自回归模型、解集模型、散粒噪声模型、非线性模型和非参数模型等［11－12］。除这些基于随机过程理论的模型之外，利用随机模拟产生的洪峰和时段洪量，放大修匀典型过程线生成洪水过程也是一种简便模拟方法［3］，如肖义等［13］利用从洪峰和洪量Copula联合分布中抽样产生的洪峰和洪量，放大修匀典型过程线生成洪水过程线。由于多维Copula函数的参数估计、函数类型选择和拟合优度检验较为复杂，目前Copula函数研究和应用多限于二维［14－15］。而且采用Copula函数模拟洪水过程时，需先构造联合分布再从联合分布中抽样，计算较为复杂。为此本文采用Iman和Conover提出的基于Spearman秩相关系数的相关随机变量模拟方法［16］，将拉丁抽样法产生的独立峰洪量序列转换成满足特定相关结构的洪峰洪量序列，再利用模拟的洪峰和时段洪量放大修匀典型过程线生成入库洪水过程，建立了基于秩相关随机变量模拟的洪水过程模拟方法。利用这一方法模拟入库洪水过程，采用Monte Carlo法估计防洪风险率，构建了水库防洪风险估计模型。并将其应用于潘家口水库主汛期汛限水位调整的防洪风险分析中。

1 研究方法

1.1 基于Spearman秩相关随机变量模拟的入库洪水过程模拟

选择洪峰和两个时段洪量作为随机变量，入库洪水过程模拟具体步骤如下。

（1）采用式（1）计算洪峰和洪量的Spearman相关系数矩阵C＝（cij）3×3，并对其进行Cholesky分解得到矩阵P＝（pij）3×3，即C＝PPT。

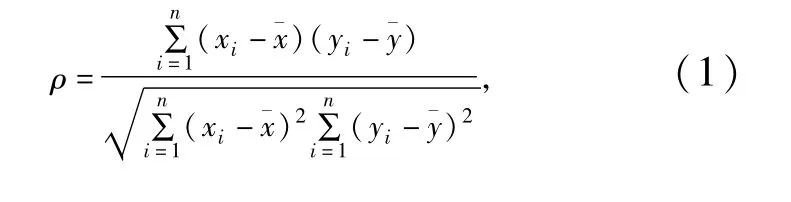
式中：n为相关变量X和Y的样本容量，xi是Xi在X中的秩，yi是Yi在Y的中的秩。

（2）按式（2）产生n维VanderWaerden Score向量Sn×1，并对向量S中的元素进行排列生成矩阵R＝（rij）n×3。

式中：φ－1（·）为标准正态分布函数的逆。矩阵R中的列向量均由向量S中的元素组成，只不过矩阵R中列向量元素在所属列中的排列顺序与向量S不同，而且矩阵R中各列向量中相同元素的排列顺序也不完全相同。

（3）求矩阵R的Spearman相关矩阵T＝（tij）3×3，并对矩阵T进行Cholesky分解得到矩阵Q＝（qij）3×3，即T＝QQT。

（4）依据式（3）对矩阵R进行转化得到矩阵Rb＝（rbij）n×3。

（5）依据洪峰和时段洪量的分布特征，采用拉丁抽样法产生服从P－3分布的独立随机数矩阵U。拉丁抽样法具有抽样效率高、遍历性、能有效控制随机模拟的误差等优点，可提高模拟精度［17］。采用拉丁抽样法产生服从P－3分布随机数时，首先产生n个服从U（0，1）分布的随机数ui，然后计算概率pi＝（i－1）／n＋ui／n，其中i＝1，2，…，n，最后用求逆法产生P－3分布随机数xi＝F－1（pi），其中F－1是P－3分布的逆函数，可采用数值方法［18］求逆。

（6）依据矩阵Rb中第j列元素的秩对矩阵U中第j列元素进行排序得到矩阵Vn×3。

（7）依据模拟的洪峰和时段洪量，采用鲍尔明法［19－20］修匀放大典型洪水过程线，最终得到n条入库洪水过程线。

由以上模拟步骤知，基于Spearman秩相关随机变量模拟的入库洪水过程模拟方法具有以下优点：①简便高效。模拟过程中不必从洪峰洪量联合分布中抽样，而只需通过矩阵变换将独立的洪峰洪量序列转换成相关序列。②可用于多站洪水等复杂洪水过程模拟。相对于单站洪水过程模拟，多站模拟的随机变量维数随站数成倍增加，而且需要考虑各站之间的洪峰洪量相关关系。由上述模拟步骤知，模拟计算量随随机变量维数增加呈线性增长，不存在“维数灾”问题；而且对随机变量间相关结构没有限制，因此这一模拟方法适合于多站洪水等复杂洪水过程模拟。

1.2 水库防洪风险率估算

将调洪最高水位Zm等于或高于控制水位Zd的概率定义为水库防洪风险率。其中水库控制水位Zd主要包括大坝防浪墙高程、坝顶高程和校核洪水位等。对于给定的汛限水位方案，采用Monte Carlo估计及防洪风险步骤如下：首先，根据水库调度规则，对随机模拟生成的n条入库洪水过程线分别调洪演算，得到n个调洪最高洪水位Zm；然后统计Zm等于或者超过Zd的次数m，依据下式计算防洪风险率Pf。

2 实例应用

2.1 水库概况

潘家口水库位于河北省唐山市与承德地区的交界处，是引滦工程的主要蓄水工程。水库设计标准为1 000年一遇，校核标准为5 000年一遇。现行汛限水位216.00 m，设计洪水位224.50 m，校核洪水位227.17 m。潘家口水库汛期被划分成3个分期，其中主汛期是7月1日－8月20日。主汛期设计洪水成果如表1所示［21］。主汛期现行调度方案是以1962年洪水和500年一遇洪水的调洪高水位作为分级控泄的。具体的调度规则见文献［21］。

2.2 计算过程

根据潘家口水库1954－2002年49年洪水资料，分别计算了主汛期洪峰Qmax、最大3 d洪量W3和最大6 d洪量W6之间的Pearson和Spearman相关系数，结果见表2。由表2可知，主汛期洪峰与洪量的相关系数均非常高，说明洪峰与洪量显著相关。利用本文建立的模拟方法，共模拟生成了40万组Qmax、W3和W6。表1中给出了模拟出的洪峰和洪量序列统计参数。由该表可知，模拟序列各统计参数均与实际值非常接近，误差非常小。表2中给出了Sperman相关系数的实际值与模拟值对比结果同。表2中，相关系数的实际值与模拟值也非常一致，误差也很小。综合表1和表2可知，模拟序列很好地反映潘家口水库入库洪水统计特征，可用于后续计算。表明本文所建立的入库洪水过程模拟方法能很好地保持洪峰洪量统计特征和相关结构，可用于洪水过程随机模拟。

潘家口水库共有1958、1959和1962年3条典型洪水过程线。为分析典型过程线对防洪风险率的影响，分别采用这3条典型过程线以及综合典型过程线，生成4种不同类型的入库洪水过程线，进行模拟计算。其中综合典型过程线是指按照选择概率从3条典型过程线中随机抽取一条过程线作为典型。3条典型过程线洪峰流量出现概率分别为96.323%、89.317%和98.046%。洪峰流量小于1959年典型过程线洪峰的概率为89.317%，位于1959和1958年典型过程线洪峰之间的概率为7.006%，位于1958和1962年典型过程线洪峰之间的概率为1.723%，将这三个概率的归一化值作为选择概率，则三条典型过程线的选择概率分别为7.146%、91.097%和1.757%。

表1 潘家口水库主汛期洪峰洪量统计参数的实际值与模拟值对照表

表2 洪峰洪量相关系数的设计值与模拟值对照表

从216.0～220.0 m每抬高0.5 m作为一个调整方案，共设计了9个主汛期汛限水位调整方案。在调洪演算之前，先计算出不同汛限水位方案的两级调洪高水位（即1962年洪水调洪水位和500年一遇洪水调洪水位）［21］。以校核洪水位227.17 m为控制水位。利用Monte Carlo法，估算了不同汛限水位方案在不同典型过程线下的防洪风险率，结果见表3和图1。

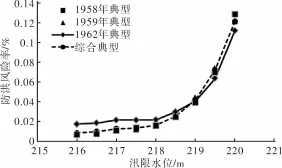
图1 各典型过程线的主汛期防洪风险率

表3 潘家口水库不同汛限水位下防洪风险率计算结果

综合分析表3和图1可得以下结论：

（1）随着汛限水位抬高，防洪风险率逐渐增大。随着汛限水位抬高，4种不同典型过程线的防洪风险率都在增大，且当汛限水位超过218.0 m后，风险率增幅都显著增大。为控制汛限水位抬高带来的防洪风险，潘家口水库主汛期汛限水位上限值控制在218.0 m。这一结果与文献［21］中汛限水位风险效益综合评估结果一致。

（2）典型过程线的选择对防洪风险率有一定的影响。峰现时间和涨落过程的差异导致同一汛限水位下不同典型过程线的防洪风险差别较大。其中1962年典型过程线计算出的风险率明显偏大，汛限水位调整的空间较小；而综合典型由于考虑了入库洪水的各种可能，计算出的风险率介于其他3种典型过程之间。汛限水位分析论证时应考虑典型过程线选取对防洪风险的影响。

3 结论

利用基于Spearman秩相关随机变量模拟方法，将拉丁抽样法产生的独立洪峰洪量序列转换成满足特定相关结构的洪峰洪量序列，再利用模拟的洪峰和时段洪量放大修匀典型过程线生成入库洪水过程，建立了入库洪水过程随机模拟方法。这一模拟方法简便高效，可用于多站洪水等复杂洪水过程模拟。利用该方法模拟入库洪水过程，采用Monte Carlo法估计防洪风险，构建了水库防洪风险估计模型。将该模型应用于滦河流域潘家口水库主讯期汛限水位调整的防洪风险估计中。应用结果表明：水库主汛期水位上限值控制在218.00 m；所建立的入库洪水过程随机模拟方法简便有效，可以用于洪水过程随机模拟；构建的防洪风险估计模型计算结果客观合理，在洪水资源安全利用系统风险分析中具有一定的推广应用价值。

［1］ 胡四一，高波，王忠静，等.海河流域洪水资源安全利用—水库汛限水位的确定与运用［J］.中国水利，2002（10）：105－108.

［2］ 高波，王银堂，胡四一.水库汛限水位调整与运用［J］.水科学进展，2005，16（3）：326－333.

［3］ 程亮.计算统计学方法在洪水资源利用的风险管理中的应用研究［D］.合肥：合肥工业大学，2010.

［4］ 丁晶，邓育仁，侯玉，等.水库防洪安全设计时设计洪水过程线法适用性的探讨［J］.水科学进展，1992，3（1）：45－52.

［5］ 熊明.三峡水库防洪安全风险研究［J］.水利水电技术，1999，30（2）：39－42.

［6］ 陈元芳.随机模拟法与传统方法推求设计防洪库容优劣的初步研究［J］.水科学进展，2000，11（1）：64－69.

［7］ 冯平，韩松，李建.水库调整汛限水位的风险效益综合分析［J］.水利学报，2006，37（4）：451－456.

［8］ 冯平，韩松.提高水库汛限水位的防洪风险分析［J］.天津大学学报，2007，40（5）：525－529.

［9］ 陈士永，王祥三，张涛，等.Copula函数和AR模型在洪水随机模拟中的应用［J］.水电能源科学，2009，27（2）：55－57.

［10］罗启华，周研来，杨娜，等.基于SAR模型和蒙特卡罗法的防洪调度风险分析［J］.人民长江，2011，42（1）：4－8.

［11］王文圣，金菊良，李跃清，等.水文随机模拟进展［J］.水科学进展，2007，18（5）：768－775.

［12］金菊良，潘金锋，张礼兵，等.洪水多站峰量同时模拟的随机模型［J］.灾害学，2003，18（1）：9－14.

［13］肖义，郭生练，熊立华，等.一种新的洪水过程随机模拟方法研究［J］.四川大学学报：工程科学版，2007，39（2）：55－60.

［14］郭生练，闫宝伟，肖义，等.Copula函数在多变量水文分析计算中的应用及研究进展［J］.水文，2008，28（3）：1－7.

［15］肖名忠，张强，陈晓宏，等.珠江流域干旱事件的多变量区域分析及区域分布特征［J］.灾害学，2012，27（3）：12－18.

［16］Iman R L，ConoverW J.A distribution-free approach to inducing rank correlation among input variables［J］.Commun.Statist-Simula.Computa.，1982（11）：311－334.

［17］刁艳芳，王本德.基于不同风险源组合的水库防洪预报调度方式风险分析［J］.中国科学：技术科学，2010，40（10）：1140－1147.

［18］Armido R DiDonato，Alfred H Morris.Computation of the incomplete gamma function ratios and their inverse［J］.ACM Transactions on Mathematical Software，1986，12（4）：377－393.

［19］鲍尔明.一种设计洪水过程线放大方法的探讨［J］.水文，1984，4（3）：24－28.

［20］王锐琛，杨百银.一种设计洪水过程线放大方法［J］.西北水电，1994（1）：1－5.

［21］刘克琳.水库汛限水位调整与风险研究［D］.南京：南京水利科学研究院，2006.

Risk Evaluation Model of Reservoir Flood Control Based on Sam pling Rank Correlated Random Variables

Cheng Liang1，Wang Zongzhi1，Jin Juliang2，3，Liu Kelin1and Wu Chengguo2，3
（1．State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Nanjing Hydraulic Research Institute，Nanjing 210029，China；2．School of Civil And Hydraulic Engineering，Hefei University of Technology，Hefei230009，China；3．Institute ofWater Resources and Environmental Systems Engineering，Hefei University of Technology，Hefei230009，China）

A flood risk evaluationmodel based on sampling rank correlated random variables is introduced.In themodel the Latin samplingmethod is used to generate independent flood peak and volume series，and a correlated random variables samplingmethod inducing the desired spearman correlation rank correlation coefficientmatrix is used to convert the independent series to related series.The flood process is amplified and smoothed by the typical hydrograph and the simulated flood peak and volume series.The flood control risk rate is evaluated by Monte Carlo simulation.Thismodel is applied to Panjiakou reservoir located in Luanhe river basin.Two conclusions are reached：1）The upper limit of flood control water level for the main flood season is 218.00 m；2）The flood process simulation model is simple to use and effective and the flood risk analysis resultwas objective and reasonable.The proposed method is suitable for risk analysis of flood resources utilization.

risk evaluation of reservoir flood control；utilization of flood resources；seasonal flood controlwater level；rank correlated random variable；flood simulation

S761 X43

A

1000－811X（2014）04－0020－04

10.3969／j.issn.1000－811X.2014.04.004

程亮，王宗志，金菊良，等.基于秩相关随机变量模拟的水库防洪风险估计［J］.灾害学，2014，29（4）：20－22，42.［Cheng Liang，Wang Zongzhi，Jin Juliang，et al.Risk Evaluation Model of Reservoir Flood Control Based on Sampling Rank Correlated Random Variables［J］.Journal of Catastrophology，2014，29（4）：20－22，42.］

2014－05－08

2014－06－26

水利部公益性行业专项经费基金资助项目（201201022，201301003）；国家自然科学基金资助项目（51309072，51279223，51309004）；安徽省自然科学基金（1208085ME75）

程亮（1985－），男，湖北浠水人，博士研究生，从事水资源系统模拟调控研究.E－mail：chengliang＠nhri.cn

金菊良（1966－），男，江苏吴江人，博士，教授，从事水资源系统工程研究.E－mail：JINJL66＠126.com