基于ANSYS的轿车副车架动力学拓扑优化

杨章程，陈丽丽，李剑敏

（浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州310018）

基于ANSYS的轿车副车架动力学拓扑优化

杨章程，陈丽丽，李剑敏

（浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州310018）

以上海大众某车型的前副车架为研究对象，建立了副车架的有限元模型，通过ANSYS进行自由模态试验，验证了模型的准确性；对副车架进行频率拓扑优化，根据得到的拓扑密度云图对副车架模型进行了参数优化，模态分析计算的结果表明优化后副车架的振型与原模型保持一致，低阶固有频率有显著提升，固有频率得到了优化。

模态分析；拓扑优化；模态试验

0 引 言

近年来国内外学者在以频率为优化目标进行优化方面进行了诸多研究，并在结果上达成了优化目的。2002年，Chandrasekaran A K等［1］选用轻型车车架的前三阶振动频率作为优化目标，进行多步拓扑优化得到X型横梁的最优拓扑结构。2007年，Laxman［2］针对某车型出现悬架系统上控制臂的应力太高、一阶固有频率太低的问题来对悬架控制臂进行形状优化，使其一阶频率有大幅度的提高而最大应力下降30%。2009年，王登封等［3］应用拓扑优化方法，针对某商用车车身设计中的固有频率作为约束条件，选用焊点体积最小作为优化模型的目标函数，进行优化，通过优化结果得到的焊点满足了设计的要求，并且在车身焊点数量上相比于原结构大幅度减少。

本文以上海大众某车型的前副车架为研究对象，综合ANSYS模态分析、模态试验、基于频率的拓扑优化等多学科方法进行分析研究，经优化后的副车架在振型基本不变的前提下，能提高低阶固有频率，取得明显的优化效果，从而避免副车架与发动机产生共振。

1 基于ANSYS副车架自由模态分析

副车架是中高档轿车底盘的重要部件，在底盘上起着承载、减振和集成零件的作用。注意到副车架为钢板冲压焊接结构，因此采用SHELL63壳单元进行网格划分。副车架材料为汽车结构钢，弹性模量为206 GPa，泊松比为0.3，密度为7.8 g/cm3，设置单元格最小尺寸为5 mm，副车架总共划分为26 153个单元，77 218节点，建立的有限元模型如图1所示。

图1 副车架有限元模型

运用ANSYS软件进行自由模态分析，得到副车架前12阶固有频率和各阶振型如图2。由于自由模态的前六阶为刚体模态，频率为0，没有分析意义；从第七阶模态开始提取，共提取6阶模态和其对应的振型。表1为副车架频率值及各阶振型的分析说明。

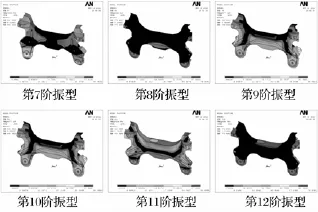
图2 副车架振型

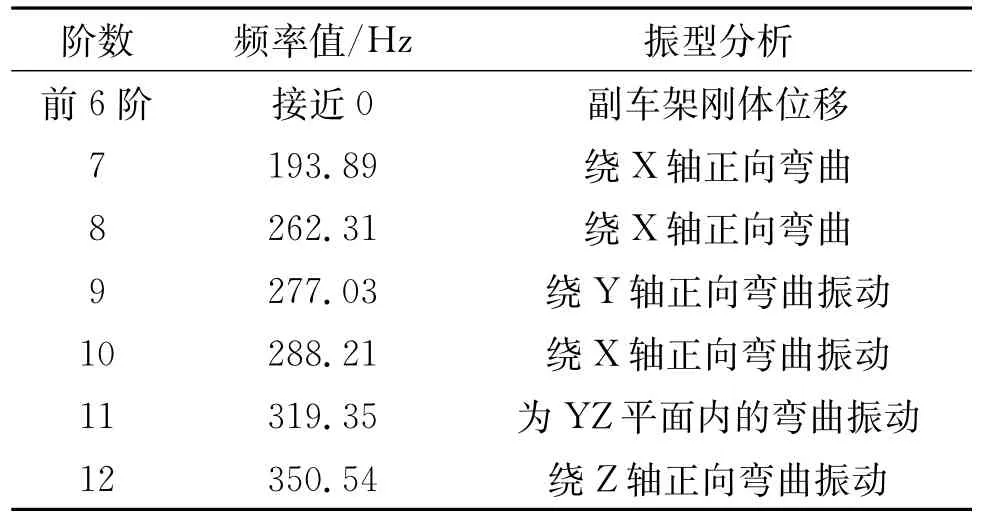
表1 副车架频率值及各阶振型

2 副车架试验模态分析

进行结构的模态试验，以验证有限元模型的准确性。用4根橡皮绳，在副车架与车身相连的4个连接点处进行悬吊，橡皮绳弹性较好，其与副车架等重物体组成单自由度系统的固有频率约为10Hz左右，远小于副车架第一阶频率，可以认为副车架处于自由支承状态，如图3所示。

图3 自由支承的悬架模式

考虑到副车架为体型较小、较刚硬的构件，其单点激励方式亦可获得较高的频率精度，故实验采用力锤单点敲击激励。将传感器粘贴在振动幅度也即变形比较大的地方，尽量避开节点，如图4所示。

图4 传感器粘贴位置

本实验选择的触发参数为自由采集方式，允许系统不做任何等待，立即进入信号采集状态，并且连续采集。根据力锤及加速度传感器参数对其进行标定，然后按图5连接好实验设备系统。

图5 模态分析实验设备系统组成

以力锤敲击触发随机信号进行激振，数据采集与分析系统对采集的信号进行处理，经傅氏逆变换得到相应的脉冲响应函数，再经计算得到所需的模态参数（图6-图9）。在数据采集与分析系统中，识别出副车架除刚体模态外的前6阶模态参数，并与有限元仿真的结果作一对比，如表2所示。

图6 频谱信号

图7 时域响应信号

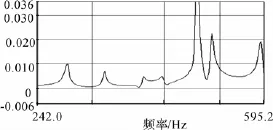
图8 频域响应信号

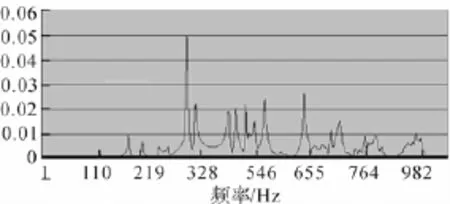
图9 低阶模态数值

通过比较自由模态下试验及有限元结果，模态频率的相对误差及相对误差均方根值均小于5%，两者符合良好。因此，认为有限元模型能够较好地反映了副车架的动力学特性，表明所建立的有限元模型正确。

3 基于频率的副车架拓扑优化

在有限元理论中，结构的固有频率振动方程为［］：

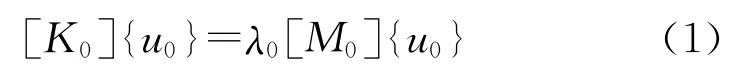
式中：［K0］、［M0］为结构的刚度矩阵和质量矩阵；［u0］为模态矩阵；λ0=为特征值对角阵。

在优化中，如果从结构中删除第e个单元会引起刚度矩阵和质量矩阵产生相应变化。

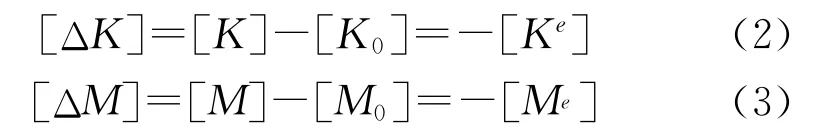
式中，［Ke］、［Me］分别为第e个单元的刚度与质量矩阵。

于是优化结束后的方程（3）简化为：

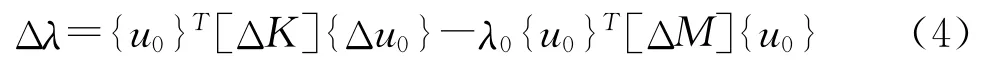
将（2）、（3）带入上式，可得：

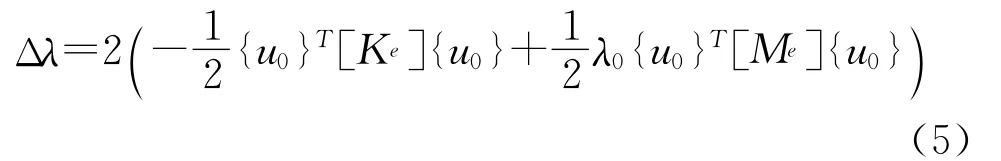
如果定义Ve、Te分别为单元模态的应变能和单元模态动能，则

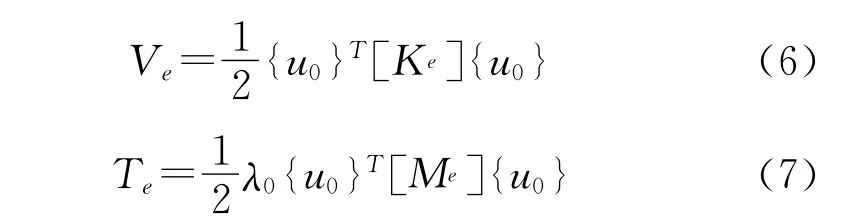
则方程（5）可写成：

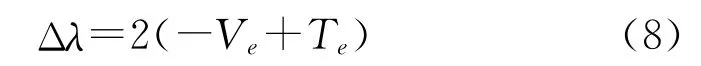
为消除单元尺寸的影响，可定义结构单元模态刚度灵敏度为：

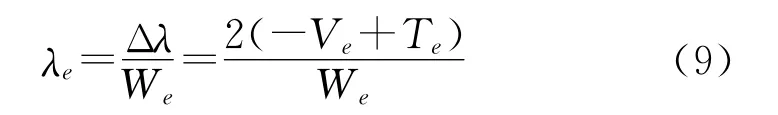
式中，We为第e个单元的体积，或称动刚度灵敏度。

由方程（9）可见，单元拓扑修改模态刚度灵敏度不仅与单元模态应变能有关，还与单元模态动能有关。一般说来，如果单元被删除将使结构刚度下降从而使固有频率降低，但单元被删除将使结构质量减小而使频率增加。因此，如果优化目标要求结构的质量最小，并使模态刚度（频率）提高，则最有效的方法即是删除具有模态刚度灵敏度较低的单元。根据方程（9）计算每一单元模态（动）刚度灵敏度（j=1，2，…K，n），并计算无量纲系数：

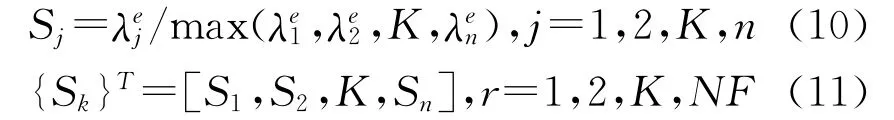
max（λej）为在所有单元中具有最大模态刚度灵敏度的单元；NF为分析所提取的模态数；Sj为0～1之间的无量纲系数。结构动态拓扑优化中，用下式作为删除单元的准则：

式中，Sc为预先给定的确定删除单元的阀值。当第j个单元的模态刚度灵敏度满足准则（12），则第j单元将被删除，反之则保留［5］。

在ANSYS中进行拓扑优化，得到单元伪密度分布图（如图10），蓝色部分显示的为将要去除材料部分，红色部分显示的为将要保留的材料部分。黄色所显示的为拓扑优化设计变量相对较大值（0.5～1），也将保留。

4 模型修改及模态分析

从图10中发现第七阶频率对副车架与车身处附近的单元最灵敏，但是删除连接点附近的材料显然不能满足副车架的功能性，所以本文对副车架与车身连接点附近的蓝色区域进行减薄处理，使其厚度由原先的2.5 mm减为1.5 mm（在学位论文《轿车副车架的结构优化及轻量化设计》中已验证了其符合强度设计。

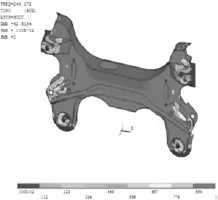
图10 拓扑优化密度云图

为了验证优化结果的可靠性，对改进后的副车架进行模态分析计算，并列出了前6阶的固有频率，结果如表3所示，相应的各阶振型如图11所示。对比原副车架结构与优化后的前6阶振型（图2和图11），可知副车架的振型与原模型基本保持一致，而7～12阶频率都得到了相应的提高，具体增幅如表3，实现了提高固有频率的优化目标。

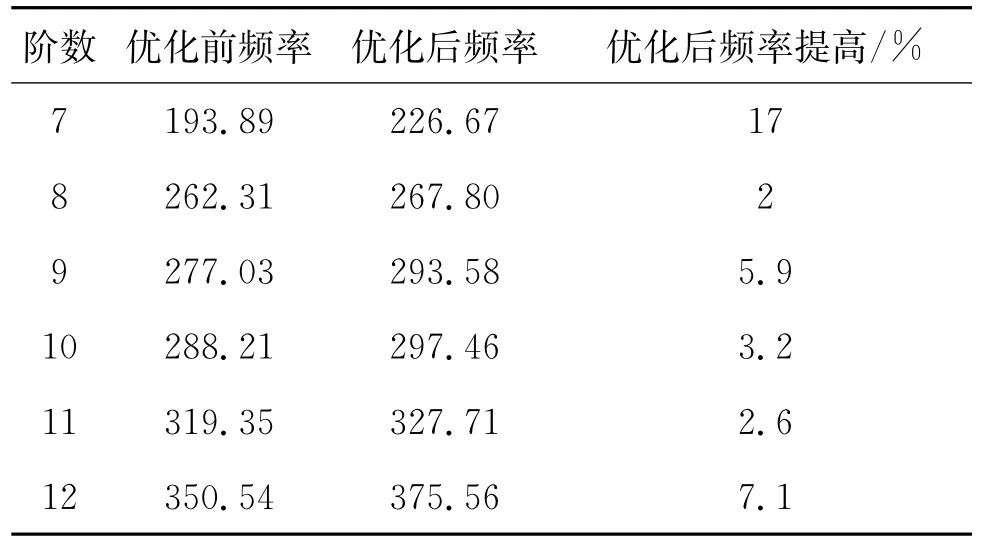
表3 优化后模态阶数的频率及优化前后对比

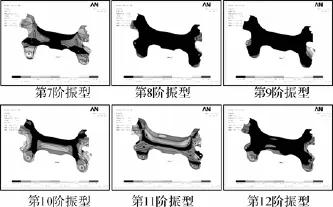
图11 优化后副车架低阶模态对应的振型

5 结 论

a）对副车架在ANSYS中进行模态分析，得到各阶振型及固有频率值；对比试验模态结果，两者相对误差及相对误差均方根值均小于5%，表明有限元模型能够较好地反映了副车架的动力学特性，证明所建立的有限元模型正确。

b）以频率为目标对副车架进行拓扑优化，根据拓扑密度云图对副车架模型修改，对副车架与车身连接点附近的不敏感区域进行减薄处理，使其厚度从由2.5 mm减为1.5 mm。

c）对改进后的副车架进行模态分析计算，副车架的振型与原模型保持一致，但低阶固有频率值都得到一定的提高，实现了提高固有频率的优化目标。

［1］Chandrasekaran A K，Solimana，Josephsonj，et al.Design optimization of heavy vehicles by dynamic simulations［J］.SAE Paper，2002（1）：30-51.

［2］Laxman S，Mohan R.Structural optimization：Achieving a robust and light-weight design of automotive components［J］.SAE Paper，2007（1）：7-18.

［3］王登峰.商用车驾驶室白车身焊点缩减拓扑优化研究［J］.汽车工程，2009，31（4）：326-330.

［4］郭立群.商用车车架拓扑优化轻量化设计方法研究［D］.长春：吉林大学，2011.

［5］陈 猛.轿车副车架设计与优化［D］.合肥：合肥工业大学2010.

［6］冯 桢，于 涛，曾齐福.拓扑优化方法在产品设计中的应用探索［J］.机械设计与制造，2007（3）：138-139.

Dynamic Topology Optimization of Auxiliary Frame of Passenger Cars Based on ANSYS

YANG Zhang-cheng，CHEN Li-li，LI Jian-min
（Zhejiang Key Laboratory of Reliability Technology Research for Mechanical and Electrical Products，Zhejiang Sci-Tech University，Hangzhou 310018，China）

Taking the former auxiliary frame of one vehicle model of Shanghai Volkswagen as research object，this paper establishes a finite element model for auxiliary frame，and verifies the accuracy of the model with free modal test by ANSYS；conducts topology optimization of frequency for auxiliary frame，obtains the cloud picture of topology density and modifies the geometric model.Modal analysis and calculation results showed that the optimized auxiliary frame vibration model consistent with the original model，the inherent low-order frequency is greatly improved and the optimization objective of improving the inherent frequency is realized.

modal analysis；topology optimization；modal test

U469.11

A

（责任编辑：张祖尧）

1673-3851（2014）01-0020-04

2013-09-15

杨章程（1989-），男，温州永嘉人，硕士研究生，主要研究方向是机构学与机械动力学。