碳纤维复合材料等效建模与电磁特性分析

廖 意, 张 元, 王 义, 吴琪琳

(1.上海市航空航天器电磁环境效应重点实验室,上海 200438;2.武汉军械士官学校,湖北 武汉 430075;3.东华大学纤维材料改性国家重点实验室,上海 201620)

碳纤维复合材料等效建模与电磁特性分析

廖 意1, 张 元1, 王 义2, 吴琪琳3

(1.上海市航空航天器电磁环境效应重点实验室,上海 200438;2.武汉军械士官学校,湖北 武汉 430075;3.东华大学纤维材料改性国家重点实验室,上海 201620)

针对碳纤维复合材料细观结构的电磁模型剖分和求解困难的问题,采用均匀化方法建立了复合材料的等效层模型,并用于碳纤维复合材料的反射系数、透射系数和屏蔽效能的计算。选取了三种不同物理结构的复合材料模型进行验证,等效层模型的计算结果与采用有限元数值软件的结果进行了对比,当纤维周期远小于波长时,等效层模型具有很好的精度,最后分析了物理参数变化对复合材料电磁特性的影响。

碳纤维；复合材料；等效建模；反射系数

0 引言

碳纤维复合材料(Carbon Fiber Reinforced Composite,CFRC)具有高强度、耐腐蚀、抗疲劳等优异性能,被广泛应用于现代航空和航天工业。波音B787、空客A380、战斗机、无人机等大量采用了复合材料,以降低重量［1］。虽然碳纤维复合材料在力学和热学等方面具有显著的优点,但是导电性能和电磁屏蔽特性远远低于传统的金属材料,外部电磁信号很容易耦合进入碳纤维复合材料结构体内,导致电磁干扰(Electromagnetic Inference,EMI)。近些年,复合材料的电磁特性研究已成为研究人员关注的热点。

复合材料的特征参数可以采用实验方法进行测量,如材料的反射系数、透射系数等,从而确定材料的等效电磁参数。国内外有较多文献对此作了介绍［2-5］。但是,实验方法往往成本高、周期长,且要求在碳纤维复合材料结构体已经成型情况下进行测试。通常,设计师希望在材料制造之前就能对等效电磁参数进行预测和分析,这也是现代材料设计的要求［6］。

理论上,采用数值计算方法能够比较精确地分析出复合材料的电磁特性。然而,由于碳纤维复合材料内部细观几何构型极为复杂,往往存在很大的未知数,导致计算工作的极大困难。国内外上世纪80年代开始研究关于复合材料计算的简化方法,采用有效媒质理论求得复合材料的等效电磁参数,经典的计算公式有Maxwell-Garnell方程、Bruggeman公式、QCA-CPA(准晶近似-相干势近似)公式等［7］,多数利用各组分的电磁参数以及体积比进行计算。针对周期结构复合材料,出现了均匀化方法(Homogenization Method),利用周期结构中电磁场的宏观特性预测材料的电磁参数［8］。

本文将采用均匀化方法,首先建立碳纤维复合材料的等效层模型,然后基于传输线理论推导出复合材料的反射系数、透射系数以及屏蔽效能的计算公式,并对建立的等效层模型进行验证,最后讨论了等效层模型的频率适用范围。建立的等效层模型可以用于复合材料屏蔽性能或吸波性能等的分析。

1 碳纤维复合材料的等效层模型

单层碳纤维复合材料结构如图1(a)所示。这是一种二相介质材料,碳纤维在x方向周期排列,外部以基体材料(如环氧树脂)包裹。基体材料的介电常数为εm,磁导率为μm,碳纤维介电常数为εf,磁导率为μf。单层材料表现出非均匀且各向异性的特点。图1(b)为复合材料在xy平面的截面图,单层厚度为L,碳纤维直径为D,纤维结构周期为P。

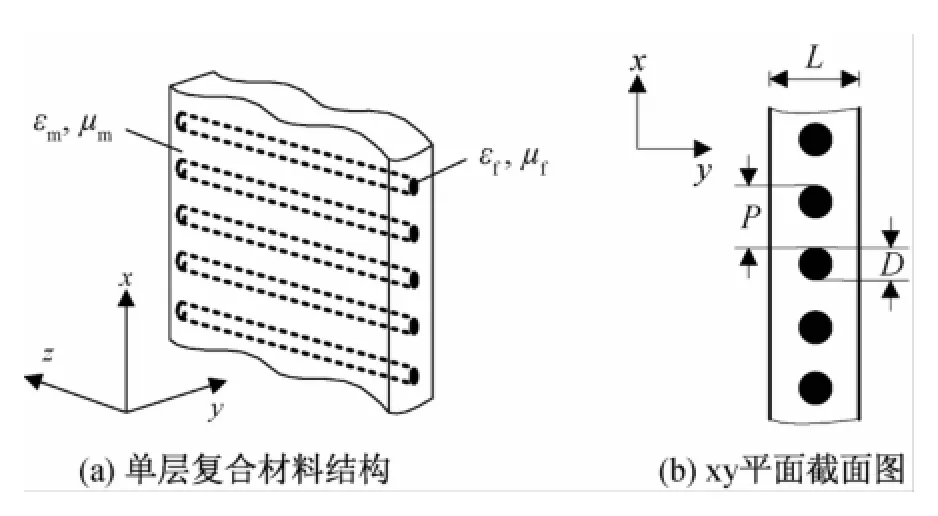
图1 单层复合材料结构与坐标关系

根据均匀化方法［8］,当碳纤维结构周期相对于波长较小时,可将复合材料结构视为等效媒质,平均电场和磁场仍然满足麦克斯韦方程组［9］。等效后的材料为均匀各向异性,电磁特性可以用张量形式的介电常数［ε］和磁导率［μ］表示。

式中:εx、εy、εz分别表示x方向、y方向和z方向的介电常数;μx、μy、μz分别表示x方向、y方向和z方向的磁导率。

式中:g为碳纤维在基体材料中所占的体积百分数。根据图1(b)的结构关系可以得出

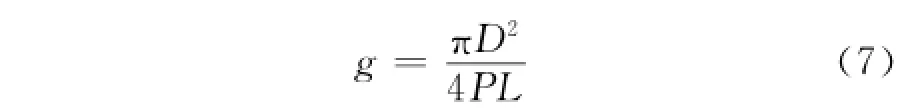
2 复合材料电磁特性计算

以两层复合材料为例,利用等效层模型可以导出反射系数、透射系数和屏蔽效能的计算公式,单层和两层以上材料的计算可以同理推出。

图2(a)为两层复合材料及坐标关系,假设:电磁波为平面波,并沿+y方向入射,电磁波依次经过空气、复合材料A、复合材料B、空气;复合材料A中碳纤维按z方向排列,复合材料B中碳纤维按x方向排列;介电材料磁导率为μ0。

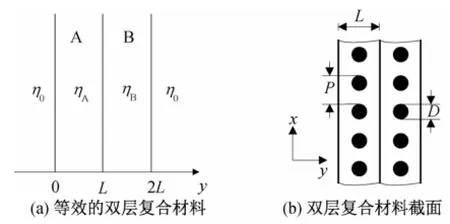
图2 双层复合材料

由图2(a)可见,复合材料A和复合材料B的输入波阻抗分别为ηA和ηB,厚度都为L,y＜0和y＞2L的区域都为空气。根据传输线理论,在分界面y=2L处的反射系数R2L和透射系数T2L分别为

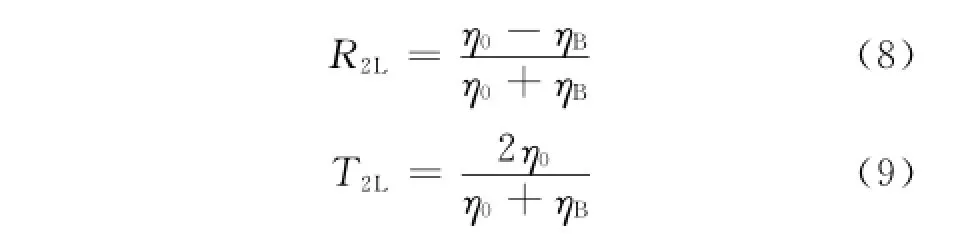
在分界面y=L处的反射系数RL和透射系数TL分别为

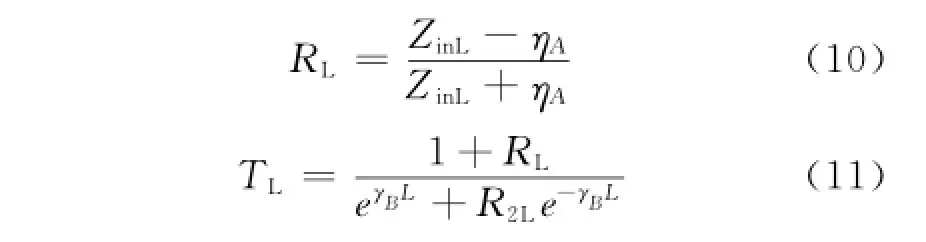
式中:ZinL为分界面y=L处的输入阻抗。

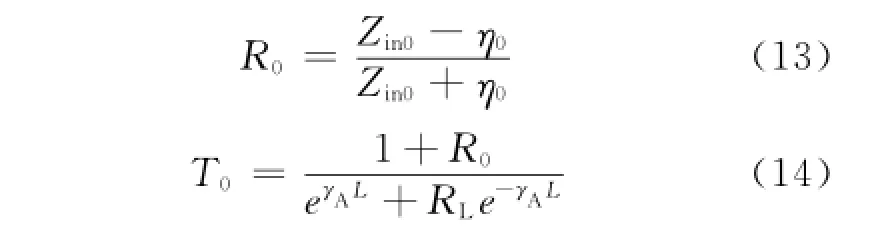
总的透射系数T为图2(a)中三个界面透射系数的乘积:

屏蔽效能是透射电场与入射电场比值,用分贝(dB)表示时的计算式为

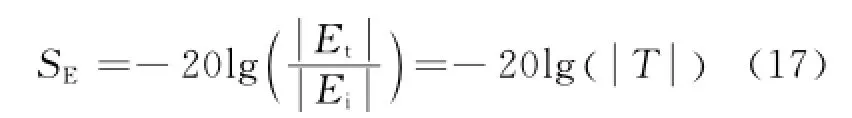
当电磁波由+y方向入射,电场在x方向极化时,复合材料A中的介电常数用εx表示,对应地,复合材料B中的介电常数则需要用εz表示,用于求解反射系数、透射系数和屏蔽效能。这里只考虑了电磁波垂直入射且电场在x方向极化的情况,由于复合材料的电磁特性是用张量形式计算出来的,故对于任意入射角与任意极化方向都是有效的。

3 等效模型验证与讨论

选取了三个不同的复合材料结构模型作为示例(其中部分结构为文献［9］的实例),对等效层模型计算的结果与采用有限元方法计算的结果进行比较,并分析了不同物理参数对复合材料电磁特性的影响。

3.1 实例验证

［示例1］

复合材料的参数为D=7.5 mm,P=15 mm, L=15 mm,基体材料相对介电常数εmr=2,纤维相对介电常数εfr=4,纤维电导率σ=0 S/m。当电场分别在x方向极化和z方向极化时,材料的反射系数结果如图3所示。

图3 示例1中复合材料的反射系数

可以看出在较低频率,等效层模型计算结果与有限元法计算结果接近。随着频率的升高,当结构周期尺寸约为四分之一波长时,纤维材料与基体材料接触面的电磁效应不可忽视,平均场概念不再适用,等效模型计算结果的误差逐渐增大。

［示例2］

复合材料的参数为D=0.05 mm,P=0.1 mm, L=0.75 mm,εmr=2,εfr=2,σ=10 000 S/m。反射系数的计算结果如图4(a),纤维间距P很小时,在频率范围10 GHz以内,两种算法的结果吻合较好。屏蔽效能计算结果如图4(b),当电场在x方向极化时,屏蔽效能很低,电磁波几乎全部透射,而当电场在z方向极化时,屏蔽效能达到30 d B以上。在频率20 GHz以上时,等效层模型计算结果的误差较大。

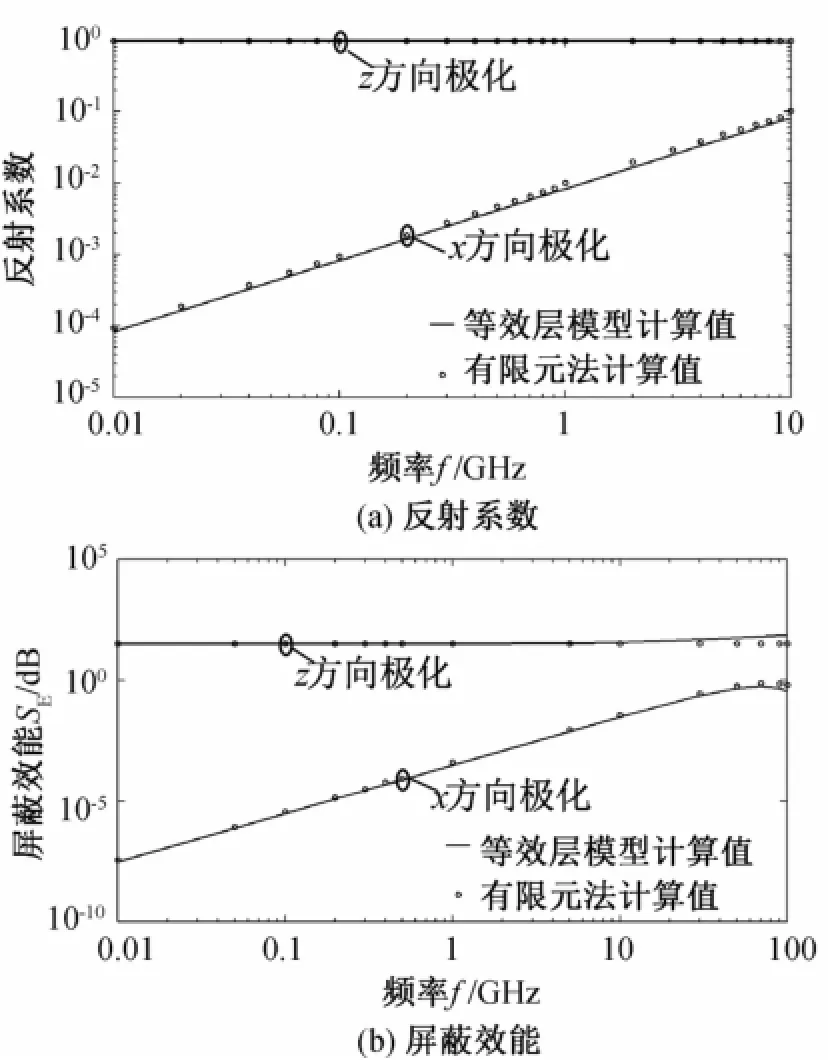
图4 示例2中复合材料的反射系数和屏蔽效能

［示例3］

双层的复合材料结构各层材料的物理参数与示例1相同,复合材料A中碳纤维按z方向排列,复合材料B中碳纤维按x方向排列,此时电磁特性与电场极化方向无关。反射系数和屏蔽效能的计算结果如图5所示。

图5 示例3中复合材料的反射系数和屏蔽效能

可以看出,从4 GHz开始,等效层模型计算结果的误差变大,等效层模型已经无法描述实际结构的谐振特性。

3.2 不同参数对电磁特性影响分析

当结构周期远小于波长时,等效层模型能够精确地描述实际复合材料。利用示例2中的几何模型,设置不同纤维的电导率、纤维的直径、基体材料的介电常数、纤维材料的介电常数,如表1所示。

表1 碳纤维复合材料参数

利用等效层模型计算不同物理参数对复合材料电磁特性的影响。计算得出的反射系数如图6～图9所示。

图6表明,随着纤维的电导率升高,z方向极化入射电场的反射增大,即提高了屏蔽效能,而x方向极化的反射系数不受影响。

图7表明,增加纤维的直径导致纤维紧密排列,增大了对x和z方向极化电场的反射。

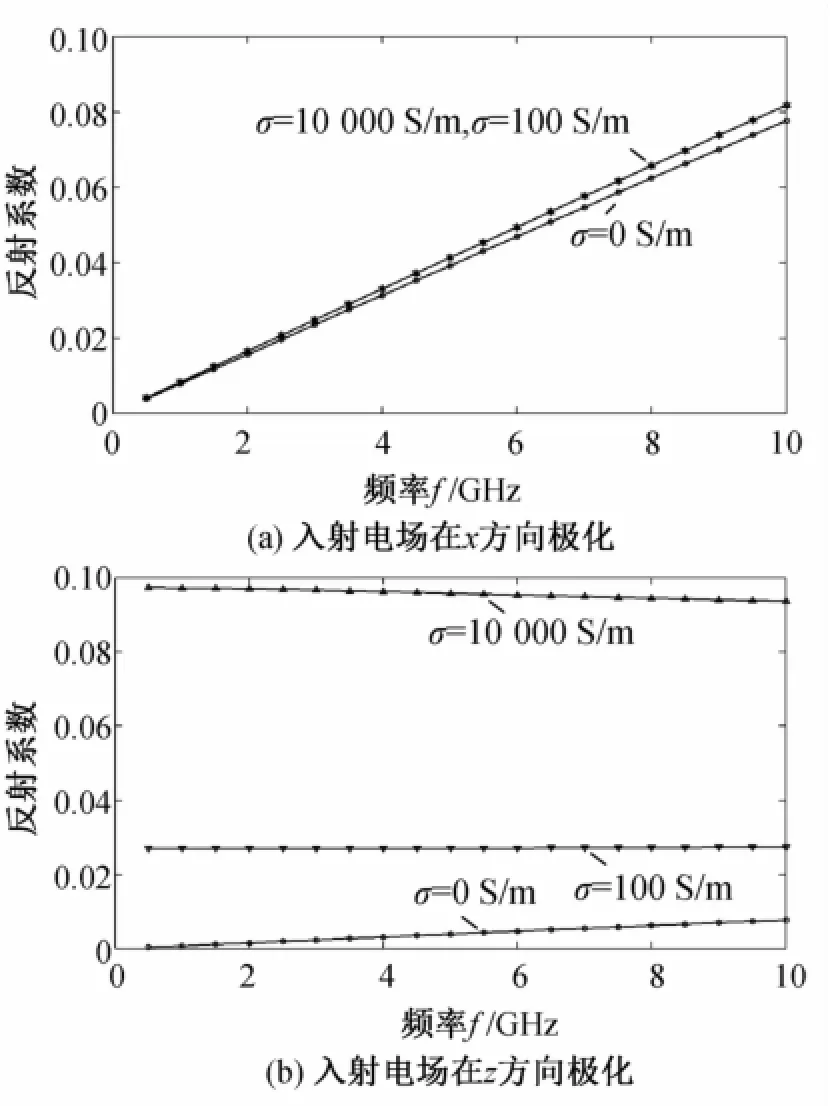
图6 σ取不同值时材料的反射系数

图7 D取不同值时材料的反射系数

图8表明,增加基体材料的相对介电常数,对z方向极化电场的反射影响较小,对x方向极化电场的反射将增大。

图8 εmr取不同值时材料的反射系数

图9表明,增加纤维的相对介电常数,对电磁波的反射和屏蔽性能几乎无影响。

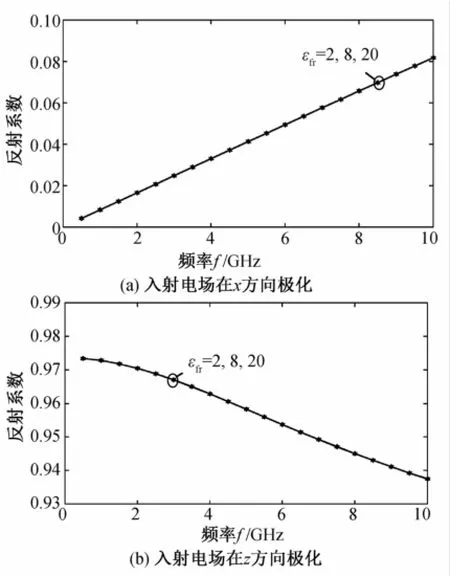
图9 εfr取不同值时材料的反射系数

4 结束语

碳纤维复合材料结构参数的非均匀各向异性以及细观几何构型的复杂性,给电磁计算带来了许多困难。采用均匀化方法建立复合材料的等效层模型,可以根据传输线理论直接计算碳纤维复合材料的反射系数、透射系数和屏蔽效能。实例验证表明,当纤维结构周期不超过四分之一波长时,等效层模型具有较高精度。随着频率升高,纤维表面电流及纤维间相互作用使得平均场概念不再适用,等效层模型误差增大。此外,利用等效层模型对不同物理参数复合材料电磁特性的分析,表明碳纤维复合材料具有明显的各向异性特点,沿入射电场方向的高电导率碳纤维对屏蔽效能起主要作用。

［1］Rosa I M D,Sarasini F,Sarto M S,Tamburrano A.EMC Impact of Advanced Carbon Fiber/Carbon Nanotube Reinforced Composites for Next-Generation Aerospace Applications［J］.IEEE Transaction on Electromagnetic Compatibility, 2008,50(3):556-563.

［2］Holloway C L,Hill D,Ladbury J,Koepke G, Garzia R.Shielding Effectiveness Measurements of Materials in Nested Reverberation Chambers［J］. IEEE Transaction on Electromagnetic Compatibility,2002,44(2):350-356.

［3］Catrysse J A,Goeije M D,Steenbakkers W,Anaf L.Correlation Between Shielding Effectiveness Measurements and Alternative Methods for the Characterization of Shielding Materials［J］.IEEE Transaction on Electromagnetic Compatibility, 1993,35(4):440-444.

［4］Loughry T A,Gurbazani S H.The Effects of Intrinsic Test Fixture Isolation on Material Shielding Effectiveness Measurements Using Nested Mode-Stirred Chambers［J］.IEEE Transaction on Electromagnetic Compatibility,1995,37(3):449-452.

［5］朱正吼.碳纤维复合材料电磁特性研究［J］.机械工程材料,2001,25(11):14-16.

［6］张永杰,李江海,孙秦.复合材料结构等效电磁参数均匀化方法［J］.电波科学学报,2009,24(2): 280-292.

［7］于世敬,葛德彪,申宁.复合介质等效电磁参数的数值研究［J］.物理学报,2010,59(2):943-948.

［8］Kuester E F,Holloway L.Improved Low-Frequency Performance of Pyramid-Cone Absorbers for Application in Semi-Anechoic Chambers［J］. IEEE National Symposium on Electromagnetic Compatibility,1989,32(2):394-399.

［9］Holloway C L,Sarto M S,Johansson M.Analyzing Carbon-Fiber Composite Materials With Equivalent-Layer Models［J］.IEEE Transaction on Electromagnetic Compatibility,2005,47(4):833-844.

Equivalent Modeling and Analysis of Electromagnetic Characteristics for Carbon Fiber Composite Material

LIAO Yi1, ZHANG Yuan1, WANG Yi2, WU Qi-lin3
(1.Shanghai Key Laboratory of Electromagnetic Environmental Effects for Aerospace Vehicle,Shanghai 200438;2.Wuhan Ordnance Non-Commissioned Officers Academy,Wuhan Hubei 430075;3.Donghua University,State Key Laboratory for Modification of Chemical Fibres and Polymer Materials,Shanghai 201620,China)

Aiming at the fact that it is difficult to mesh and solve electromagnetic models of carbon fiber reinforced composite(CFRC)with thin fibers in the structure,the homogenization method is used to present the equivalent layer model for CFRC.This equivalent layer model is utilized to efficiently calculate reflection and transmission coefficient,as well as shielding effectiveness of CFRC.Three different physical structures of CFRC are used to validate the presented equivalent layer model.The results of reflection coefficient and shielding effectiveness obtained from the equivalent layer models are compared to results obtained from a full numerical solution based on the finite-element(FE)method of the actual periodic fiber composite.It shows that the equivalent layer model is reasonably accurate when the period of a periodic structure is smaller than wavelength.Moreover,the effects of physical parameterson the EM characteristics of CFRC analyzed by using the equivalent layer model.

carbon fiber;composite material;equivalent modeling;reflection coefficient

TN011

A

1671-0576(2014)04-0001-06

2014-09-15

上海市优秀技术带头人项目的资助,课题编号14XD1423100;上海市科学技术委员会的资助,课题编号14ZR1439400、12ZR1430400。

廖 意(1984―),男,博士,工程师,主要从事电磁兼容技术研究。