基于有限元的微型二维力传感器设计及贴装优化
2014-05-25沈荣
沈 荣
(上海机电工程研究所,上海 201109)
基于有限元的微型二维力传感器设计及贴装优化
沈 荣
(上海机电工程研究所,上海 201109)
为了实现导弹在飞行过程中空间力的测量,运用有限元的方法实现了对一种新型多维力传感器的设计,选用E型圆膜片式结构作为多维力传感器的弹性体,运用ANSYS建立弹性体的有限元模型,并进行了网格划分。根据传感器的实际工况进行了二维力传感器的静力学分析,通过分析得到了弹性体的应变特性,根据应变特性确定了二维力传感器的组桥和贴片方式,并对二维力传感器进行了模态分析,得到了二维力传感器的动态性能指标和工作带宽,基于有限元分析完成了对二维力传感器的研制和设计。
力传感器;弹性体;模态分析
0 引言
多维力传感器可以检测三维空间多个方向的力或力矩信息,自上世纪70年代问世以来,首先在智能机器人领域得到应用。近年来,在航空、航天、机械装配与制造以及体育竞技领域也得到了广泛应用。而由于多维力传感器具有测力信息丰富、测量精度高等特点,在力及力-位控制场合也得到了广泛应用,尤其在航空机器人、航空航天飞行器、航天宇宙空间对接仿真、导弹扭力测试、火箭推力测试等场合发挥极其重要的作用[1]。国内,中国科技大学、华中科技大学、大连理工大学和哈尔滨工程大学等在机器人多维力传感器方面的研究起步较早,并取得了一定成果,但国内针对于航空航天这种特殊场合的多维力传感器的研究却很少,工业上的多维力传感器大多尺寸和重量较大,而航空航天飞行器一般体积和空间都较小。因此,传统的多维力传感器无法较好地运用到航空航天飞行器中[2]。
目前,传感器的设计主要是根据设计者经验而被动设计,针对使用特点和应用场合的主动设计和优化设计还很难做到,传感器的优化设计最根本的问题是建立传感器数学模型,由数学模型揭示传感器弹性体的应力和应变关系,诠释传感器的力学特点和维间耦合的本质关系。有限元分析方法已被广泛应用到了传感器结构设计的研究中,有限元分析在传感器的设计中发挥着越来越重要的作用。在应变式多维力传感器的设计中,有限元法可用来分析弹性体结构设计、尺寸优化和应变片在弹性体上的粘贴位置,研究传感器的静态特性、动态特性。在传感器的设计过程中,使用有限元法可以大大节约研发时间,对传感器进行有限元分析已经是传感器研发必不可少的一个过程。
针对目前工业上多维力传感器体积大、重量大等问题,本文运用有限元方法设计了一种导弹上专用的微型多维力传感器,可以实现导弹在飞行过程中轴向力和径向剪切力的测量。本传感器选用E型圆膜片式结构作为多维力传感器的弹性体,运用ANSYS建立弹性体的有限元模型,并进行了网格划分,根据传感器的实际工况进行了二维力传感器的静力学分析,通过分析得到了弹性体的应变特性,根据应变特性确定了二维力传感器的组桥和贴片方式。并对二维力传感器进行了模态分析,得到了二维力传感器的动态性能指标和工作带宽,基于有限元分析完成了对二维力传感器的研制和设计。
1 弹性体的设计
目前,市面上高维力传感器较多,低维的力传感器却较少,为了实现对空间中轴向拉压力和径向剪切力的测量,本文设计一种新型的二维力传感器,传感器采用同一个弹性体来实现对轴向拉压力和径向剪切力的测量。
图1为E型圆膜片结构图,主要尺寸包含内径a、外径b以及膜厚h,E型圆膜片中间凸起的部分是硬中心,硬中心直接承受作用力,E型圆膜片通常用作敏感集中力、压力的敏感元件,用来测量压力作用下的应变变化。
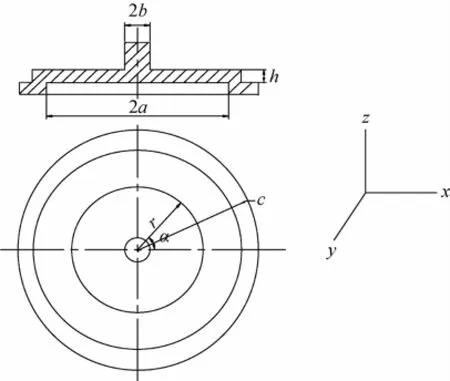
图1 E型圆膜片
图1中r为弹性体表面上的任意半径,范围为0≤r≤a;a为弹性体表面与水平面的任意夹角范围为0°≤a≤360°;c为传感器弹性体安装基座的半径。
E型圆膜片具有以下优点:
a)E型圆膜片具有应力集中、特性设计较灵活的特点;
b)在E型圆膜片的内、外边缘,由被测量引起的径向受力状态(可以通过应力与应变来反映)是相反的,即一边处于拉伸状态,一边处于压缩状态;
c)可以实现多参数的测量,不仅可以实现对压力的测量,还可以实现对差压、集中力与加速度的测量。
基于以上的分析,最终采用E型圆膜片式结构作为二维力传感器的弹性敏感元件来实现对轴向拉压力和径向剪切力的测量。为了提高传感器的灵敏度和线性度,确定传感器弹性体的尺寸,为了有限元的分析,假设外半径a=15 mm,内半径b=3 mm,安装外圈半径c=18 mm,膜片厚度h= 1 mm。
1.1 弹性体有限元模型的建立及网格划分
本文所设计的二维力传感器弹性体包括圆膜片和硬中心,它能够实现对轴向和径向应力的测量,力通过硬中心传递给圆膜片。在有限元分析前,定义传感器弹性体的材料属性,包括弹性模量和泊松比。本文采用合金钢40Cr Ni Mo作为弹性体的材料,它的弹性模量和泊松比较高,具有较好的变形和承载能力,其弹性模量为210 GPa,泊松比为0.33。
在选好材料后,要选择模型的单元类型进行建模。ANSYS提供了4种创建模型(包括实体模型和有限元模型)的方法[3]:实体建模、直接建模、输入在计算机辅助设计系统(CAD)中创建的实体模型、输入在计算机辅助设计系统(CAD)中创建的有限元模型。由于传感器结构比较简单,因此选择实体建模的方法。实体模型所选用的单元类型为SOLID186和PLANE82两种单元。对于实体建模中的面采用PLANE82单元,对于实体采用SOLID186单元。SOLID186单元具有各向异性,支持塑性、超弹性、蠕变、应力钢化、大变形和大应变能力;而PLANE82有较高求解精度,可以适应不规则形状而较少损失精度,能较好地适应曲线边界。
实体建模有4种图元,分别为:关键点、线、面、实体。建模的方式有自底向上实体建模和自顶向下实体建模,本模型的建立采用自底向上的建模方式。首先建立弹性体的10个关键点,用线将关键点依次连接成封闭的面,面的单元类型为PLANE82单元,如图2所示。

图2 弹性体关键点连接而成的封闭面
选定旋转轴线,将整个面旋转360°得到弹性体的三维实体模型,三维实体模型采用SOLID186单元。根据上面所确定的弹性体结构尺寸,建立弹性体三维实体模型,三维实体模型如图3所示。
图3 弹性体三维实体模型
在建立好几何模型后,需要对其进行网格划分,生成包含节点和单元的有限元模型[4]。本文的网格划分采用自由网格划分中的智能网格划分(SmartSize)方式,为了保证整体网格划分的均匀性,在实体建模中,在连接关键点并建立面单元后进行智能网格划分,然后再将面单元旋转成实体,网格延伸到实体。有限元模型网格划分,如图4所示。
由于硬中心所承受的力可以均匀地作用在膜片上,所以这种网格划分方式和实际情况较相符。实体模型共有99 243个节点,21 456个单元。
2.2 弹性体的有限元分析
传感器在实际使用过程中,底面的外圆圈固定,可以认为是刚性联接,因此把外圆圈的自由度设为零。由于传感器工作时所受的力可以分解为沿着轴向和径向的力,如图1所示。根据xyz坐标系的方向,确定了弹性体的受力分布情况,垂直于弹性体膜片的为z向,记为轴向拉压力,xy平面内的任意作用力为径向剪切力,因此静力分析时可以分解为两种典型的受力工况:
图4 有限元模型网格划分结果
a)垂直作用在硬中心上的轴向拉压力F1;
b)平行作用在硬中心上的径向剪切力F2;
根据传感器的量程,在传感器的硬中心上按照典型的几种工况施加一定的作用力。在z向施加F1=1 N的力,在x向施加F2=5 N的力。施加力后进行求解,可以得到在不同工况下传感器的位移、应变和应力值等。对于应变式传感器,应关注应变值,故文中给出膜片上的应变值,并加以分析。在下图的应力应变图中,x轴为对应半径的圆周长度,单位为mm,y轴为应变值。
在F1的作用下,弹性体径向应变的分布云图如图5所示。从外边缘到中心点的颜色逐渐加深,硬中心处的颜色变化最为剧烈,表明沿着x轴靠近硬中心的应变式最大,在此处贴片可以获得较大的灵敏度;图6为半径为6的圆周上的应变值,由图可以看出,相同半径上的应变值相等;图7为任意直径上的应变变化图,从图中可以看出,在任意直径上,应变关于圆心成轴对称分布。

图5 轴向拉压力作用下的应变云图
图6 半径为6的圆周上的应变值
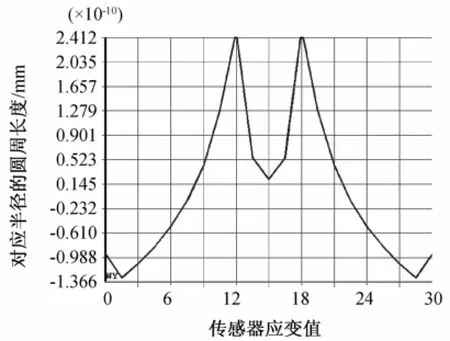
图7 直径方向上的应变值
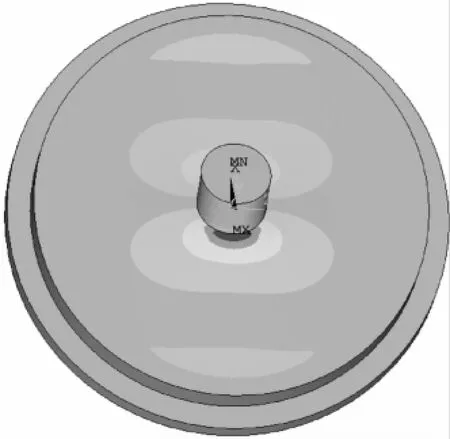
图8 径向剪切力作用下的应变云图
在F2的作用下,弹性体的应变云图如图8所示,从外边缘到中心点的颜色逐渐加深,硬中心处的颜色变化最为剧烈,应变的最大值依然出现在硬中心两侧,同时在靠近硬中心两侧的对称位置应变方向相反。图9为半径为6的圆周上的应变变化图。图10为直径上的应变变化图,从图中可以看到,硬中心两侧的应变值大小相等,方向相反,应变变化成反轴对称变化。
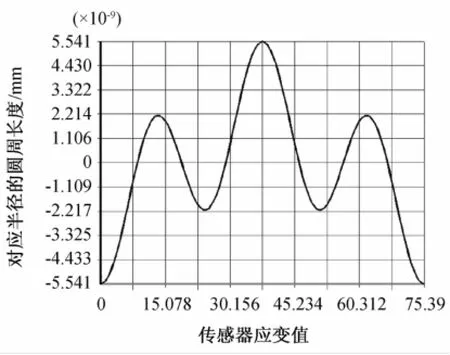
图9 半径为6的圆周上的应变值
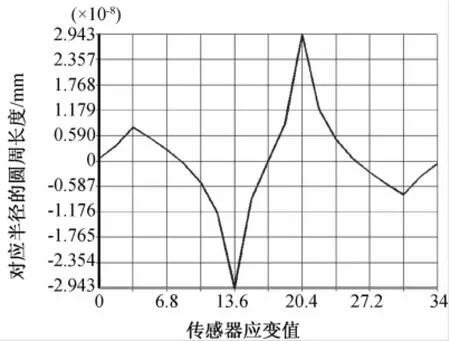
图10 直径方向上的应变值
二维力传感器要实现对轴向拉压力和径向剪切力,每4个应变片组成一个等臂全桥电路用来测量一个力,所以弹性体上总共需要粘贴8个应变片,应变片贴在弹性体的上表面[5]。根据有限元的分析,在轴向拉压力作用下,在任意一条直径方向上弹性体的应变成轴对称变化,在径向剪切力作用下,在作用力方向上弹性体的应变成反轴对称变化。根据应变片的贴片工艺和方法,最终确定应变片R2、R3、R5、R6、R7、R8粘贴在r= 4 mm的圆周上,应变片R1、R4粘贴在r=14 mm的圆周,这样也降低了对贴片工艺的要求。具体贴片和组桥方式,如图11所示。
1.3 弹性体模态分析
为了得到传感器的振型和固有频率,用ANSYS对模型进行模态分析,得到弹性体固有频率与振动模型,前6阶固有频率如表1所示。
由ANSYS模态分析结果可知(如图12~17所示):
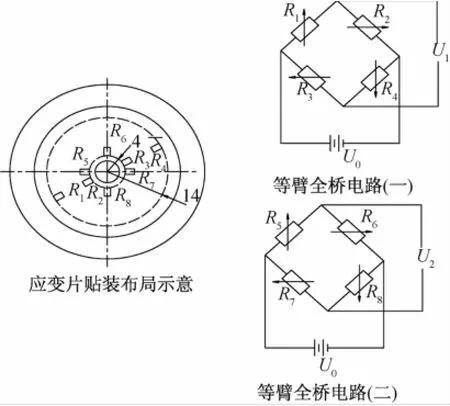
图11 传感器贴片和组桥方式
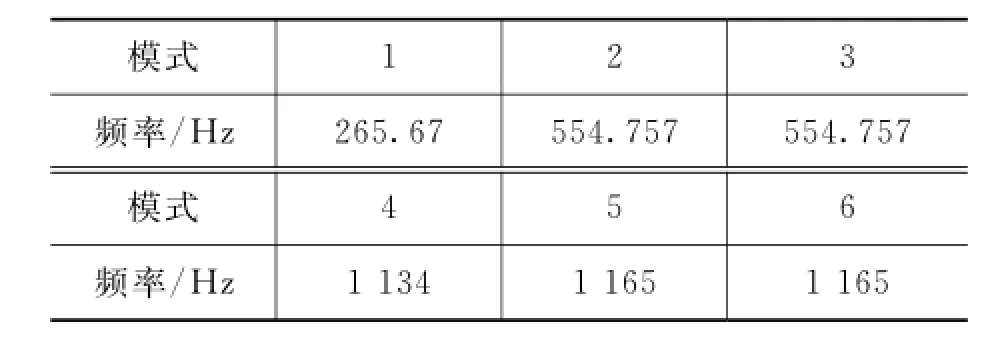
表1 前6阶频率
a)阶频率为265.67 Hz,其振型为沿z轴的平动;
b)阶频率为554.757 Hz,其振型为沿x轴的平动;
c)阶频率为554.757 Hz,其振型为沿y轴的平动;
d)阶频率为1 134 Hz,其振型为沿z轴的转动;
e)阶频率为1 165 Hz,其振型为沿x轴的转动;
f)阶频率为1 165 Hz,其振型为沿y轴的转动。
由于弹性体是对称结构,所以在x轴和y轴上的平动及转动振型是一致的,理论上频率相等。从ANSYS分析结果看,x轴和y轴上的平动、转动振型频率是完全相同的。根据经验,对于微小型结构体,一般工作带宽为第一阶频率的1/3,确定传感器的工作带宽为0~88.56 Hz,由于此传感器的工作带宽大于一般压力传感器,所设计的传感器具有很好的灵敏度和线性度。
基于传感器的静力学分析和模态分析,本文完成了二维力传感器的研制和设计,并最终进行了加工,二维力传感器实物如图18所示。本传感器的最大直径为30 mm,重量仅有9 g,极大地缩减了传感器的安装空间,达到了微型化的要求。基于ANSYS所设计的二维力传感器实现了微型化的要求,可以实现对空间轴向拉压力和径向剪切力的测量。
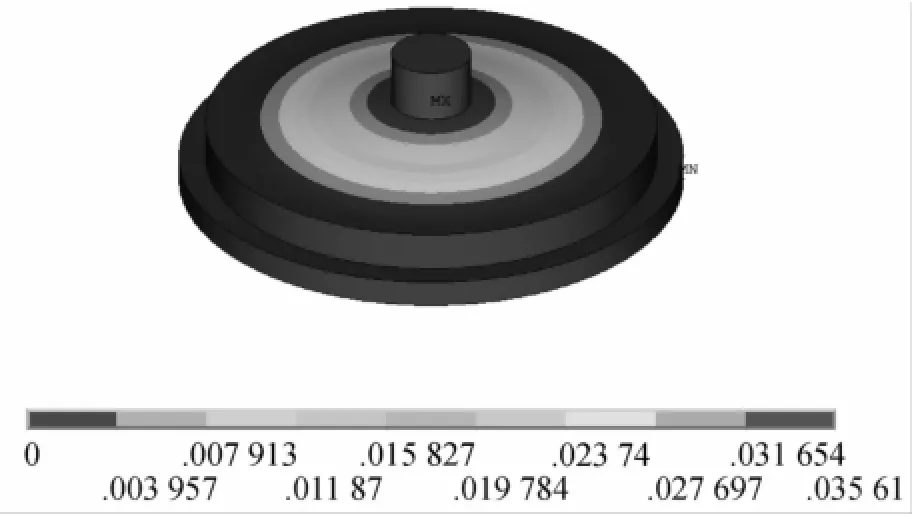
图12 第一阶振型
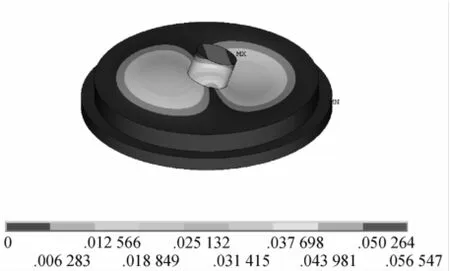
图13 第二阶振型
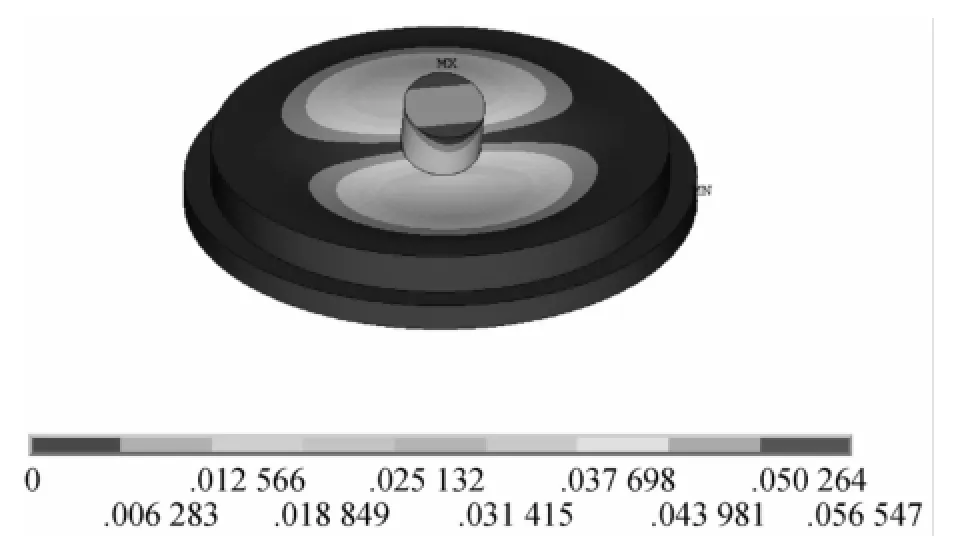
图14 第三阶振型

图15 第四阶振型
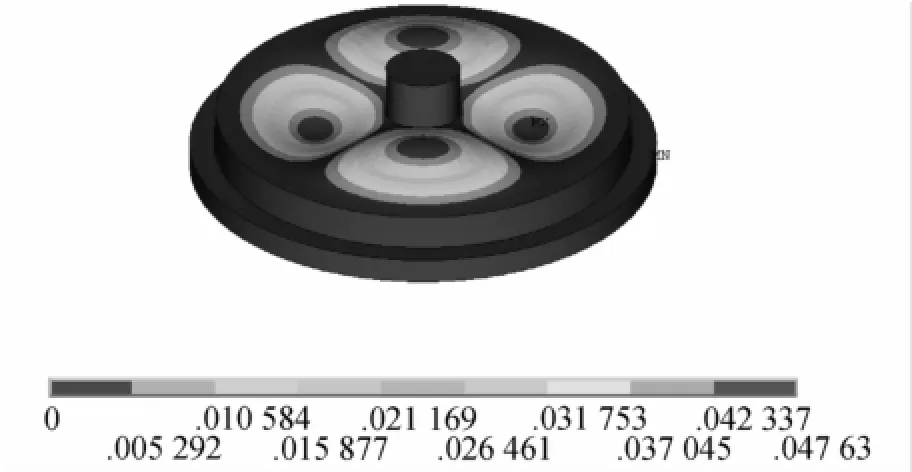
图16 第五阶振型

图17 第六阶振型

图18 二维力传感器实物图
2 结束语
为了实现对导弹在飞行过程中空间轴向拉压力和径向剪切力的测量,本文基于E型圆膜片式结构设计了一种新型二维力传感器,并运用有限元的分析方法对新型弹性体进行了建模、网格划分、静力学分析和模态分析。基于有限元分析的结果,确定了传感器的贴片和组桥方式,并确定了传感器的振型和固有频率,最终得到了二维力传感器的工作带宽,由此得出的传感器具有较好的灵敏度和线性度,同时实现了传感器微型化的要求,最大直径为30 mm,重量为9 g,大大地减少了传感器在使用过程中所占用的空间,缩小了导弹的局部尺寸。
[1]高理富,王国泰,葛运健.用于航天机器人的六维腕力传感器信号处理系统研究[J].仪器仪表与传感器,2011,24(5):16-19.
[2]高理富,宋宁,葛运建,等.航天机器人用六维腕力传感器动态特性研究[J].机器人,2002,24(4):319-323.
[3]宋爱国,黄惟一,曹效英.直接输出型机器人四维力与力矩传感器:中国,ZL031126804[P].2004,(09-19):1-7.
[4]董明,惠春,徐爱兰.基于ANSYS的压电式四臂加速度计模拟分析[J].传感技术学报,2006,19(3):637-641.
[5]Olender D,Bymes P.A Piezoelectric Force Sensor Formill-Scale Chip Refiners[J].Process Mechanical Engineering,2008:222-223.
The Design of Two-dimensional Force Sensor and the Optimization of its Placement Based on Finite Element Method
SHEN Rong
(Shanghai Institute of Mechanical and Electrical Engineering,Shanghai 201109,China)
A new type of multi-dimensional force sensor is designed based on Finite Element Method(FEM)to measure the space force in the flight process of the missile.The new sensor selects an elastomer which is a circular membrane in E-type structure.According to the actual working condition of the sensor,a static analysis of two-dimensional force sensor is established through building finite element model of elastower and meshing by ANSYS. The strain characteristic of the elastomer is obtained by FEM analysis,and a scheme of strain-measuring bridge and mount for two-dimensional force sensor is determined by strain characteristic.The dynamic performance index and work bandwidth of the sensor is obtained by modal analysis of the two-drmensional force sensor.The design and development of twodimensional force sensor based on finite element analysis is completed eventually.
force sensor;elastomer;modal analysis
TM203
A
1671-0576(2014)01-0049-07
2013-08-20
沈 荣(1980-),男,高工,主要从事军工能力和信息化建设管理工作。
