模型降阶量化反馈控制

吴雄君, 赵桂军, 吴 晔

（1.上海无线电设备研究所,上海 200090；2.上海交通大学自动化系 信息与控制教育部重点实验室,上海 200240）

模型降阶量化反馈控制

吴雄君1,2, 赵桂军1, 吴 晔1

（1.上海无线电设备研究所,上海 200090；2.上海交通大学自动化系 信息与控制教育部重点实验室,上海 200240）

针对导引头稳定平台存在严重不确定性和干扰的工况,提出一种基于渐进稳定Hutton降阶算法与量化反馈控制（QFT）相结合的模型降阶量化反馈控制方法,利用QFT设计控制器满足多种性能指标（例如鲁棒稳定性能、跟踪性能、抗干扰性能等）,采用Routh因子近似方法获得渐进稳定的降阶模型,便于工程实现。仿真结果表明,该算法对于模型和参数不确定性具有较好的鲁棒性,能满足导引头控制平台的需求。该方法相对于传统QFT设计方法更具有工程可行性。

鲁棒控制；伺服系统；导引头

0 引言

制导导弹目前处于快速发展阶段,例如飞行马赫数高、航程长、机动强,飞行过程中弹内的导引头受到严酷的热、声、振等复合环境的影响,天线系统、驱动机构甚至惯性陀螺等的固有特性会不可避免的发生改变,导引头系统的被控对象本质上为时变系统。

传统导引头系统的控制方法中,通常假定模型参数和结构相对不变,只在设计时保留一定的相角裕度和幅值裕度,或是通过振动冲击等环境试验对个别参数进行反复修正,以便设计出来的控制器具有一定的鲁棒性；对于模型为时变的情况,理论上则缺乏简单有效的频域分析工具进行处理,或者只能得到高阶的解,不利于工程实现。另一方面,现代鲁棒控制理论大多针对某一特定模型,在具体运用于导引头控制系统时,又存在理论过于复杂或假设条件过多的情况,使得工程实现极为困难［1-3］,且大多采用时域方法,很难与工程中常用的频域方法接轨。

针对上述问题,本文采用定量反馈理论（Quantitative Feedback Theory,简称QFT）对导引头稳定平台伺服控制系统进行设计,采用频域分析工具获得鲁棒性强的跟踪控制器。针对传统QFT方法回路成形设计时,通常只能得到较高阶的控制器这一不足,本文提出一种基于渐进稳定Hutton降阶算法与QFT相结合的模型降阶量化反馈控制方法［4］,有效克服不确定性,同时还能得到便于工程实现的降阶控制器。

1 概述

导引头稳定平台有多种伺服机构形式,通常具有偏航和俯仰两个正交轴系。本文以常用的齿弧式机构为控制对象进行设计分析,两通道均采用伺服电机驱动减速链的方式,由精密减速箱精确传递到天线进行运动,从而实现伺服系统的运动功能。

本文以俯仰通道稳定回路控制为例进行说明,该回路由控制器、伺服机构和陀螺构成,由参考输入和陀螺反馈信号比较获得误差信号,经控制器形成控制信号,并经功率放大送到执行元件,驱动伺服机构向误差减小的方向转动,直到伺服系统到达期望运动为止。

在传统导引头稳定平台的控制设计中,一般由某一确定试验条件获得控制对象的辨识模型,假定控制对象参数固定,未考虑参数不确定性的影响,通过稳定裕度来衡量系统工作的稳定程度即系统的相对稳定性。

实际系统考虑到导弹飞行过程中其载体内部环境条件的变化,包括弹体姿态的快速变化,会严重影响控制对象的特性,尤其是伺服机构特性性能的改变,因而要求控制器具有一定的鲁棒性能。

目前,鲁棒控制方法在理论上已经趋于成熟,通常采用的是H2、H∞控制和μ综合方法。但是由于该控制方法理论设计较复杂,涉及的数学工具较多,设计出的控制器一般多为高阶形式。另外,在实现时,面临假设条件过多无法满足的情况,因而在工程实现中一般难度较大。

QFT正是针对上述背景由以色列学者Issac.M.Horowitz教授于六十年代提出的一种频域鲁棒控制系统设计算法［1］,其主要思想是将经典控制理论中频域校正器的设计理论推广到不确定对象鲁棒控制设计中。它将被控对象的不确定范围和闭环系统频域性能指标用定量的方式在Nichols图中形成边界,以开环频率特性曲线满足边界条件为要求,通过回路成形技术对系统控制律进行设计和综合,使得所设计的控制器对模型和参数的变化具有一定的鲁棒性能。美国、以色列等国家在此领域展开大量研究,并将QFT控制理论广泛应用于各类被控对象具有严重不确定性的系统,并获得成功［5-12］。

目前,国内在这方面也投入了一定的研究,文献［3］已经研究将QFT控制方法应用在无人机控制等系统中［13-14］,获得了较好效果。需要指出的是,上述方法在具体回路成形设计过程中,常常会出现设计的控制器阶数过高的情况,主要原因是各模板单元大多为1阶或2阶惯性环节,多次累加（乘积）后容易出现高阶现象,不利于工程实现,因而迫切需要发展具有工程实用价值的QFT控制器设计方法。

2 控制目标

QFT本质上属于在频域进行设计的一种鲁棒控制设计方法,适用于导引头稳定平台这类具有不确定性和强干扰的对象,同时与传统基于频域的设计方法有较好的相容性,方便硬件测试与实现。导引头稳定平台稳定回路的原理控制框图,如图1所示。

图1 稳定回路反馈控制系统

设计控制器时,首先将对象不确定性范围和系统性能指标用定量的方式在Nichols图上形成模板和边界,进而以标称对象开环频率特性满足边界条件为目标在Nichols图形上对系统进行设计和综合,最终所设计的控制器G（s）和前置滤波器F（s）使得不确定系统的闭环传递函数能够满足性能和稳定性要求。

图1中导引头稳定回路单输入反馈控制系统包括：控制器G、被控对象P、前置滤波器F,以及反馈控制律H,噪声包括参考输入噪声W、输入噪声V、输出噪声D、传感器噪声N。

设计目标是根据鲁棒性边界指标确定控制器G,根据跟踪性能设计前置滤波器F,通过回路成形和性能验证来验证所设计的控制器G和滤波器F的性能。假定H=1,图2中所示的闭环传递函数为

式中：L（s）为系统开环传递函数,L（s）=P（s）G（s）,输入和输出干扰的闭环传递函数分别为

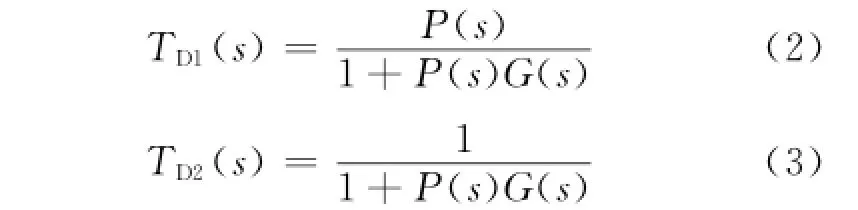
进行QFT控制器设计时,通常需要考虑下述闭环系统性能指标：

a）鲁棒稳定指标：｜L（s）/［1+L（s）］｜≤μ, μ为闭环系统允许的最大谐振幅值,单位为dB,对应于Nichos图上的一条等M圆曲线；

b）跟踪性能指标：定义鲁棒跟踪性能指标满足TL（ω）≤｜L（jw）/［1+L（jw）］｜≤TU（ω）,∀ω∈［0,∞）,其中,两个边界传递函数可以通过阶跃响应上下极限对应的频域响应得到, TU（ω）,TL（ω）为根据该响应获得的多项式；

c）抗干扰指标：｜TD1（s）｜≤BD1（jw）,｜TD2（s）｜≤BD2（jw）,其中BD1（jw）、BD2（jw）分别为给定的抗输入端干扰和抗输出端干扰性能指标。

3 QFT鲁棒控制的优化设计算法

区别于传统设计方法,本文首先采用QFT来设计控制器,并以导引头稳定回路为例阐述QFT鲁棒控制设计流程。在此基础上,发展出一种降阶的QFT算法。

QFT的设计目的是使含有不确定对象P的闭环控制系统,在指令输入r、干扰输入d1和输出干扰d2的作用下,闭环响应曲线落在给定的指标范围内。

系统在控制对象P发生一定的变化情况下,设计的控制器仍然可以满足系统的稳定性。具体的控制框图如图2所示。

图2 稳定回路控制原理示意图系统

控制系统包括：控制器G、被控对象P、前置滤波器F,以及反馈通道H。设计目标是根据鲁棒性边界指标确定控制器G,根据跟踪性能设计前置滤波器F,通过回路成形和性能验证来验证所设计的控制器G和滤波器F的性能,不失一般性,本文只重点考虑鲁棒稳定性能设计,暂不考虑滤波器F的设计优化。

3.1 降阶QFT鲁棒性控制的优化设计

为了使得闭环系统具有一定的鲁棒性,首先进行QFT设计。QFT设计通常是在Nichols图上进行的,其基本设计思想是先将对闭环系统的设计要求转化为在Nichols图上对基准对象开环频率响应曲线进行约束的一系列边界,然后通过调整基准对象的开环频率响应曲线,并使其满足边界条件来设计控制器G。将闭环系统的设计要求转化为在Nichols图上的边界是QFT设计中的重要一环。针对控制系统要求,QFT的一般设计指标包括稳定性和稳定裕度指标、跟踪性能指标、抗干扰性能指标等。下面以稳定性指标和抗干扰性能指标阐述在Nichols图上生成跟踪边界的算法流程。在进行QFT控制器设计时,考虑下述闭环系统性能指标：

a）鲁棒稳定指标：｜P（s）G（s）H（s）/［1+ P（s）G（s）H（s）］｜≤μ,μ所对应的最小幅值裕度为h=20lg（1+1/μ）,最小相角裕度为γ=180-arccos（0.5/μ2-1）；

b）抗干扰指标｜TD1（jw）｜≤BD1（jw）,｜TD2（jw）｜≤BD2（jw）

控制对象P的数学模型由电机和机构的建模获得,其中电机模型由辨识获得,具体表达式为2001/（0.0152s+1）。机构模型利用二阶模型时,常数为0.0024,阻尼系数为0.3010,表示具体如下：A-1（s）,其中A（s）=0.00242s2+2× 0.3010×0.0021s+1,陀螺模型采用二阶模型为B-1（s）,其中B（s）=0.0031832s2+2×0.7× 0.003183s+1。此处只考虑被控对象模型的不确定性,机构参数的变化最终反映到电机力矩的变化之中。

设定陀螺的参数特性在载体运动中不变,对电机和机构的模型可以近似采用二阶传递函数形式进行描述,且将不同变化因素造成的参数和模型不确定性采用如下形式：

假定上式中带有不确定性的参数名义值为k=0.126,a=66.7,b=250。另外,对于载体运动的不确定性,控制对象各参数变化范围假定在10%,具体如下：

最终降阶QFT设计算法为以下五种。

（1）确定设计要求

给定并计算出控制系统所需要的性能指标,此处稳定裕度性能参数μ取1.2。

（2）构造频率响应模板

选择一组有代表性的频率点,在每一个频率点处,求出系统的频率响应。由于系统模型具有不确定性,因此系统的响应在Nichols图上会形成一个区域,这个区域就是所谓的对象模板。控制器设计不确定模板,如图3所示。

图3 控制器设计不确定模板

频率范围内选择一个由如下独立点构成的试验频率序列w=｛0.1,1,5,10,20,30,46｝。根据3个参数k,a,b的不确定范围,共选择100个模型的状态点,并选择第50个状态点作为设计中的标称点,如图4所示。

（3）生成边界曲线

边界曲线是根据性能指标来划分的,其中包括3种典型边界曲线：跟踪边界、稳定边界和鲁棒性能边界。图5、图6、图7分别为鲁棒稳定性能及输出、输入抗干扰等几种边界的交集。

图8则给出所有边界综合,图9和图10则是设计QFT前后各种性能指标的所有边界交叉。

（4）控制器G（s）设计

图4 鲁棒幅值边界

图5 鲁棒输入干扰抑制边界

在Nichols图上,通过移动和整形基准对象的开环频率响应曲线,使其满足边界要求。具体而言,在设计过程中,通过调整增益、填加超前/滞后环节、增添实极点、零点以及负极点、零点等环节共同设计G（s）。

（5）降阶QFT鲁棒控制设计

图7 所有边界综合

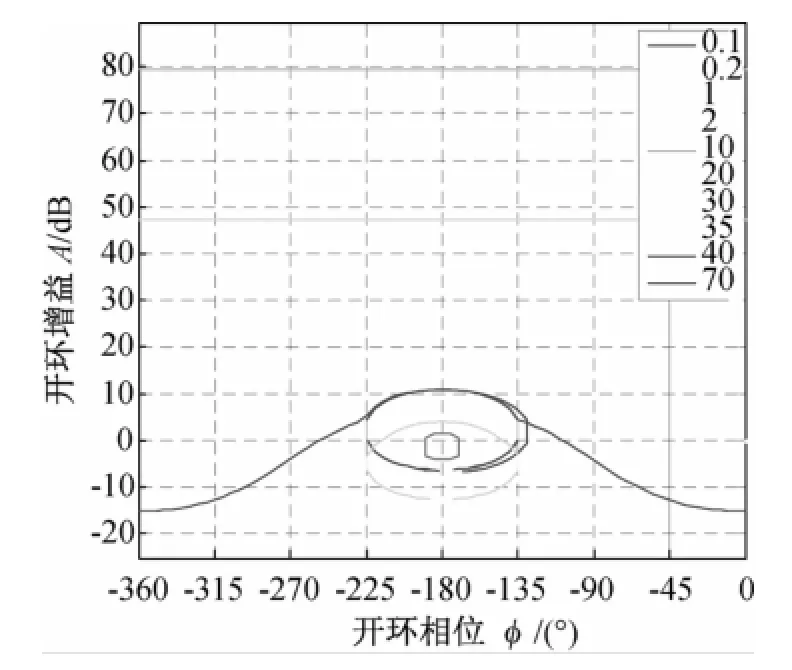
图8 所有边界交叉

图9 未设计QFT控制器前时的开环频率响应

根据零极点环节共同设计G（s）后,采用基于渐进稳定Hutton降阶算法与QFT相结合的模型降阶量化反馈控制方法,利用Routh因子近似方法获得渐进稳定的降阶模型,有效降低控制器的维数。这种方法是本文与传统QFT最大的区别。

采用步骤（1）至（5）的设计方法,最终可以获得控制器G（s）设计结果如下：

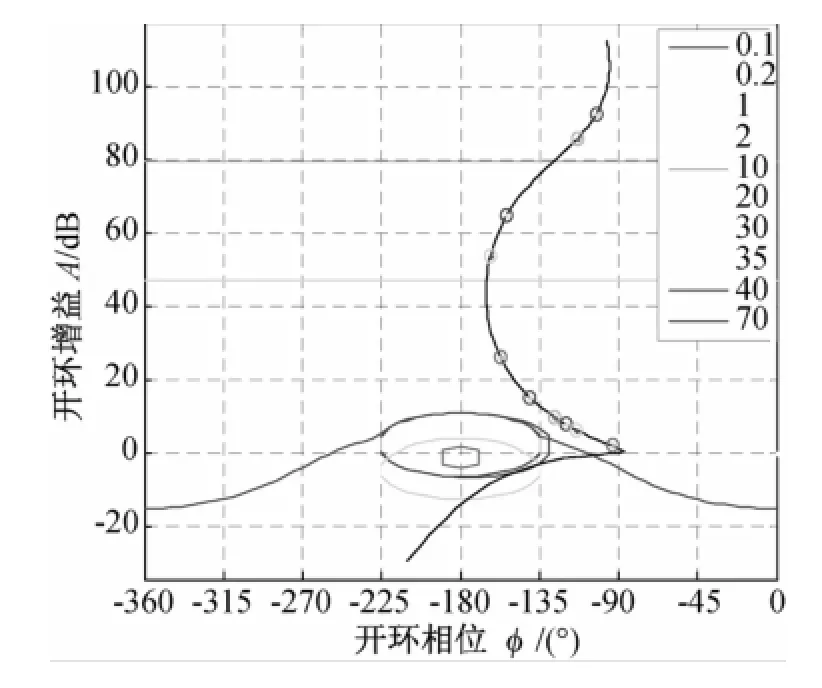
图10 控制器作用下的开环频率响应

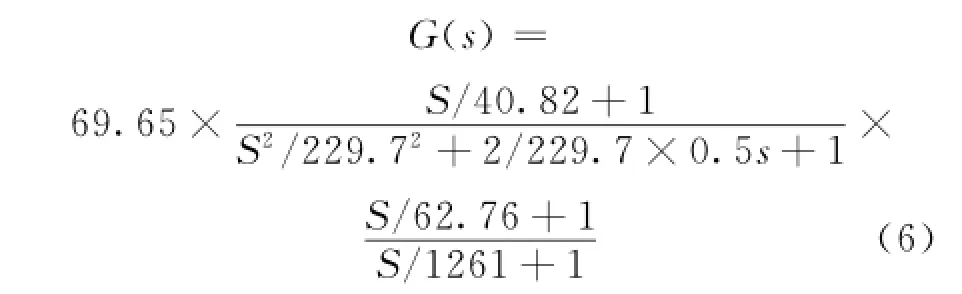
化简后可以得到

由上述算法和仿真结果可以看出：模型降阶QFT算法不需要对被控对象进行精确辨识,而只需要粗略设定被控对象阶数和参数变化范围,且控制器降阶后的模型阶数可以任意指定。另外所设计的控制器阶数低,适合于工程实现。

3.2 性能分析与验证仿真

上述降阶QFT的设计是一种近似设计,所选的对象模板和设计频率点都是有限的,设计出来的控制系统是否满足整个系统的要求,还必须通过分析才能确定。

如果控制系统不满足设计要求,应重复上述步骤选择设计点并重新设计。对设计的控制器进行性能分析,如图11至图13所示。

从图11-14中可看出控制器的设计满足了给定的动态性能指标,包括鲁棒稳定裕度和输入、输出抗干扰性能的限制。在考虑模型参数摄动时,假设电机的参数a=66.7,变化分别为名义值的80%、90%、120%、140%时,系统的阶跃响应如图14所示。

图11 系统鲁棒性能分析

图12 系统输入抗干扰性能分析

从系统的阶跃响应（如图14）可以看出,模型参数摄动时结果差异不大,超调和调节时间基本一致,说明所设计的控制系统对系统模型摄动具有一定的适应能力。

图14 参数摄动时的阶跃响应结果

4 结束语

针对导引头稳定平台工作环境恶劣,被控对象参数和结构均会发生波动,难以准确均衡鲁棒性和高性能的特点,提出一种基于渐进稳定Hutton降阶算法与QFT相结合的模型降阶量化反馈控制方法。算法不需要对被控对象进行精确辨识,并考虑了被控对象的模型不确定范围和系统的稳定性能指标、抗干扰指标,能实现一定范围参数摄动系统的强鲁棒性,控制器降阶后的模型阶数可以任意指定,相对于传统QFT设计方法更具有工程可行性。

在典型导引头控制对象的仿真结果表明,基于QFT的鲁棒控制器能够使存在严重不确定性和干扰的情况下,获得满意的控制效果,有效抑制干扰,具有较强鲁棒性。

［1］Horowitz,I.Survey of Quantitative Feedback Theory［J］.International Journal of Control, 1991,53（2）：255-291.

［2］Ying Huo,M Mirmirani,Pertros Ioannou, Mathew Kuipers.Altitude and Velocity Tracking Control for an Airbreathing Hypersonic Cruise Vehicle［J］.AIAA Guidance,Navigation,and Control Conference and Exhibit.Keystone,Colorado, USA：AIAA,2006-6695.

［3］Rueda,T.M.,Velasco F.J.Robust QFT Controller for Marine Course-changing Control［J］.5th Int.Symp.on QFT and Robust Frequency Domain Methods,Pamplona,Spain,2001：79-84.

［4］Hutton,M.,Friedland,B..Routh Approximations for ReducingOrder of Linear,Time-invariant Systems［J］.IEEE Transactions on Automatic Control,1975,20（3）：329-337.

［5］Osmon,C.,Pachter,M.,Houpis,C.H.Active Flexible Wing Control Using QFT［J］.IFAC 13th World Congress,San Francisco,CA,1996：315-320.

［6］Kelemen M.,AkhrifO.Linear QFT Control of a Highly Nonlinear Multi-machine Power System［J］.Int.J.Robust Nonlinear Control,2001,11（10）：961-976.

［7］Liberzon,A.,Rubinstein,D,Gutman,P.O.. Active Suspension for Single Wheel Statin ofOnroad Track Vehicle［J］.Int.J.Robust Nonlinear Control,2001,11（10）：977-999.

［8］YanivO.,FriedO.,Furst-Yust M.QFT Application for Headphone's Active Noise Cancellation［J］.Int.J.Robust Nonlinear Control,2002,12（4）：373-383.

［9］Gutman,P.O.,Horesh,E.,Guetta,R.,et al. Control of the Aero-Electric Power Station-an Exciting QFT Application for the 21st Century［J］. Int.J.of Robust and Nonlinear Control,2003,13（7）：619-636.

［10］Torres E.,Garcia-Sanz M.Experimental Results of the Variable Speed［J］.Direct Drive Multipole Synchronous Wind Turbine：TWT1650.Wind Energy,2004,7（2）：109-118.

［11］Garcia-Sanz,M.,Hadaegh,FY.Coordinated Load Sharing QFT Control of Formation Flying Spacecrafts［J］.3D Deep Space and Low Earth KeplerianOrbit Problems with Model Uncertainty, NASA-JPL,JPL Document,D-30052,Pasadena, California,USA,2004.

［12］Kerr,M.Robust Control of an Articulating Flexible Structure Using MIMOQFT,Ph D［M］.Dissertation,The University of Queensland,Australia,2004.

［13］Bentley A.E.Pointing Control Design for High Precision Flight Telescope Using Quantitative Feedback Theory［J］.Int.J.Robust Nonlinear Control,2001,11（10）：923-960.

［14］Dexin Xu,Kunpeng He,Yanhui Wei,Jiangpeng Zhao.Research on QFT Controller Design for LOS Stabilization System ofOpto-electronic Load for UAV［J］.10th World Congress on Intelligent Control and Automation（WCICA）,2012：1982-1986.

Reduced Order QFT Feedback Control

WU Xiong-jun1,2, ZHAO Gui-jun1, WU Ye1
（1.Shanghai Radio Equipment Research Institute,Shanghai 200090；2.Department of Automation,Shanghai Jiao Tong University,Key Laboratory of System Control and Information Processing,Ministry of Education,Shanghai 200240,China）

In order to overcome the performance degradation of the seeker platform caused by the uncertainty and disturbance in the industry scenario,an reduced order QFT control method which combines asymptotical stable Hutton reduced order algorithm and QFT design method is proposed.In this method,the QFT is adopted to design the controller to satisfy all kinds of indexes（such as robustness index,tracking performance and disturbance rejection）,then the Routh factor approximate method is used to obtain a asymptotical reduced order model,which can reduce the order of the controller efficiently and is thus suitable for application.The simulation result demonstrates the robustness against both the model and parameters uncertainty,and the proposed method can satisfy all of the performance indexes of the seeker controller platform.Compared with the traditional QFT method,it's convenient for project application.

Robust control；servo system；seeker

TJ765.331

A

1671-0576（2014）01-0001-07

2013-09-20

吴雄君（1983-）,男,博士后,主要从事约束控制、机器人视觉伺服、导引头系统控制、多智能体攻防对抗的研究；赵桂军（1976-）,高工,主要从事导引头伺服控制的研究；吴晔（1971-）,研究员,主要从事导引头伺服控制的研究。