宁波铁路南站钢结构雨棚张弦梁单侧张拉关键技术
2014-05-23江张宿
江张宿
(中铁建设集团有限公司,北京 100131)
0 工程概况
宁波铁路南站改建工程位于浙江省宁波市海曙区,在主站房的东西两侧各有一个顺轨向长147m、垂直轨道向宽184.95m的无站台柱钢结构张弦梁雨棚,总建筑面积54375.3m2。张弦梁雨棚结构呈平板状,三跨连续拱状,屋面标高15.00m,由横向张弦梁、索承系统与钢管混凝土柱组成,单个张拉单元尺寸为3×8.00m×40.85m(40.80m、37.85m)。其中横向张弦梁为实腹式矩形钢管;索承系统为一组1670级ф5镀锌钢丝双护层扭绞型船型拉索,由主索和分叉索组成、在撑杆下节点处分开,主索型号为φ5×199,分叉索型号为φ5×109,张弦梁雨棚如图1和图2所示。
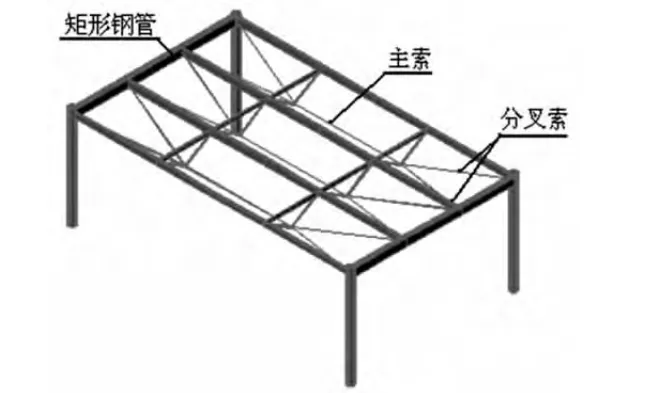
图1 单个张拉单元示意图
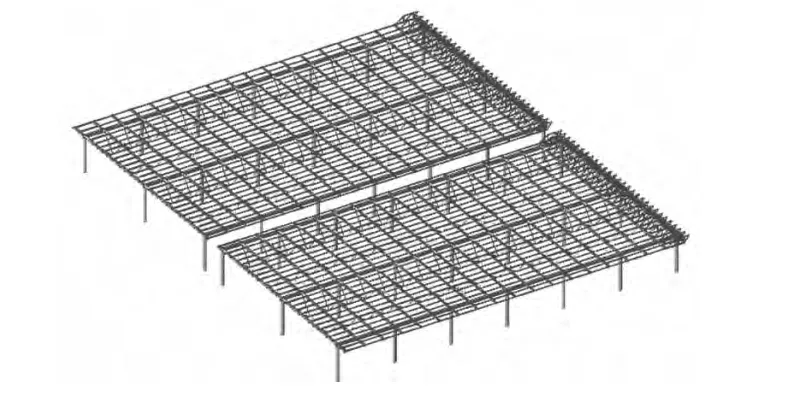
图2 西侧张弦梁雨棚轴测图
由于本工程属于既有线改造项目,雨棚施工时需确保既有铁路线的安全通行,致使部分跨线雨棚结构不能一次成跨,既有线的现状也无法实施张弦梁的两端张拉。因此,经讨论,本工程决定采用单侧张拉法,并通过攻关解决其中的关键技术,确保本雨棚工程顺利施工。
1 单侧张拉施工方案
张拉前,建立张弦梁结构的有限元模型,模拟张弦梁单侧张拉时的应力和变形状态,编制单侧张拉方案。根据有限元分析结果,深化设计和加工制作节点。张拉时,采取相邻跨单侧分级跳拉法,张拉过程逐渐增大张拉力、实时监测,监测以变形控制为主、索力控制为辅。张拉后,拆除张弦梁中部的临时支撑体系,并根据屋面变形情况,适当调整索力和变形,确保相邻张弦梁之间变形的协调性和屋面的平顺性。
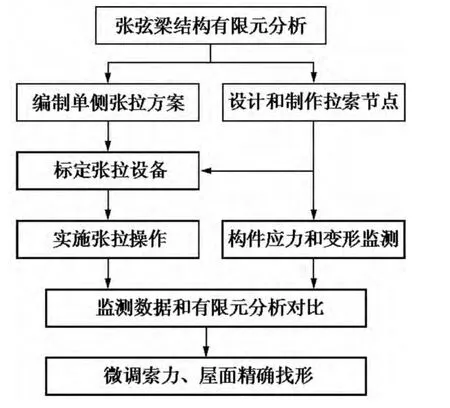
图3 单侧张拉流程图
2 关键技术研究
2.1 单侧分级跳拉方案优化
考虑宁波铁路南站既有线的施工特点和雨棚张拉后变形协调性问题,结合有限元模拟分析结果,经过方案比选,选择单侧分级跳拉法进行张拉。具体为:采用4套600kN的张拉设备(含千斤顶、油泵、压力表)对相邻的两榀梁进行单侧跳跃式张拉,每次张拉1根分叉索,张拉力分两级张拉,第1级张拉至预张力的70%,第2级张拉至预张力的100%。张拉单元和张拉走向如图4和图5所示。
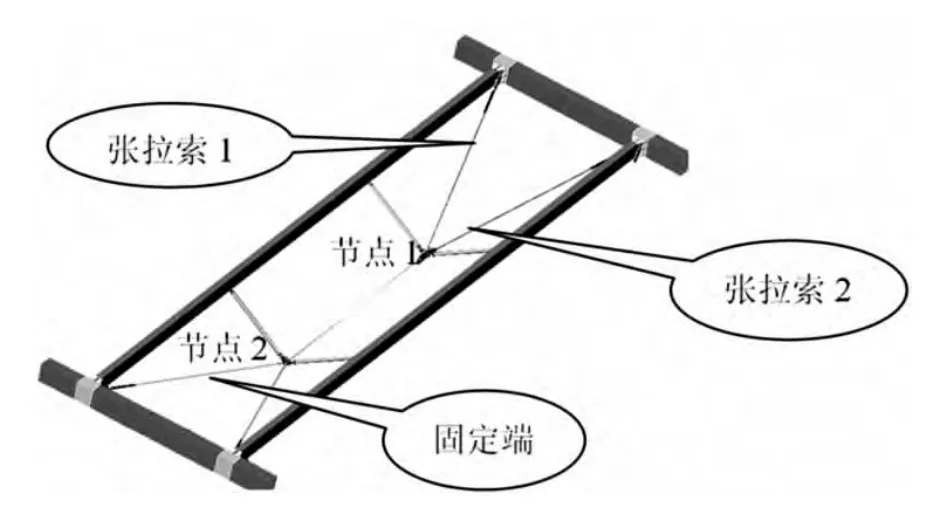
图4 单侧张拉单元示意图
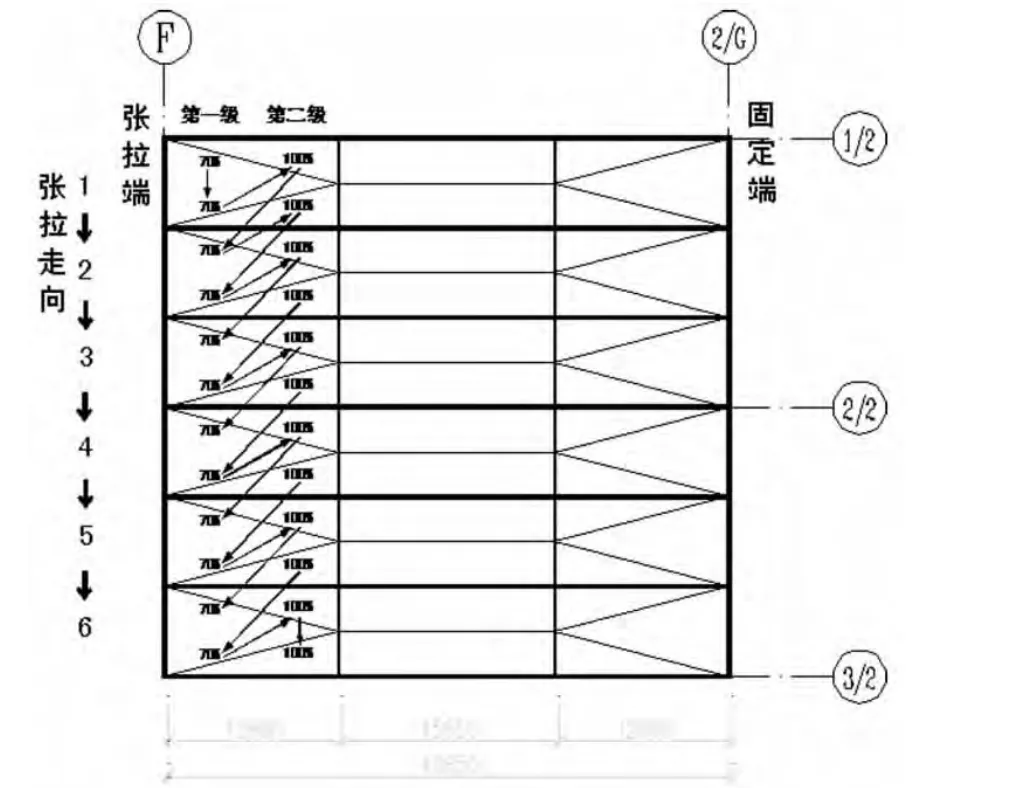
图5 单侧张拉走向图
2.2 张弦梁撑杆下节点深化设计
2.2.1 撑杆下节点构造设计
张弦梁撑杆下拉索节点是张弦梁的重要组成部分,起到连接主索和分叉索、并将张拉分力传递至上弦钢梁的作用,是顺利实现单侧张拉目标的关键所在。根据设计院要求,本工程张弦梁节点由安装单位自行深化设计。
鉴于张弦梁节点位于雨棚的最下方,是未来乘客的主视点,必须考虑美观性因素;此外,考虑到受力最优和造价最低的因素,节点采用铸钢节点、类似人字形浮漂,具体尺寸如图6和图7所示。
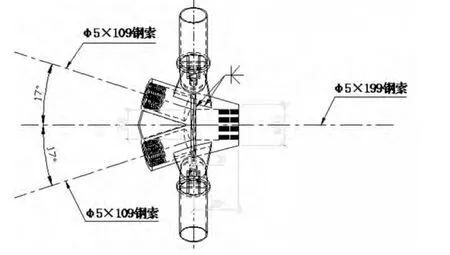
图6 撑杆下节点构造图
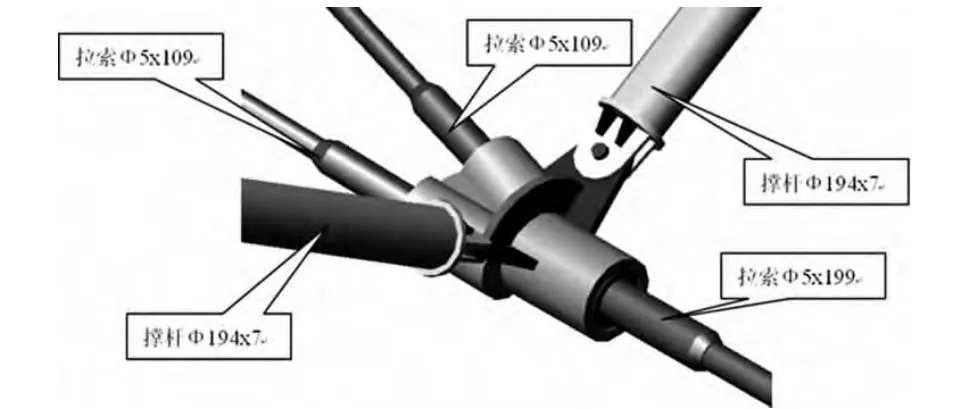
图7 撑杆下节点轴测图
2.2.2 撑杆下节点有限元分析
为了确保设计的撑杆下节点满足受力要求,对设计的节点采用ANSYS12.0进行有限元分析。由于各荷载组合包络值小于拉索破断荷载的0.4倍,且考虑节点安全系数值为1.25,计算得到主索力为3265kN,分叉索力为1790kN,两个耳板同时考虑撑杆受力因素,分析结果如图8和图9所示。
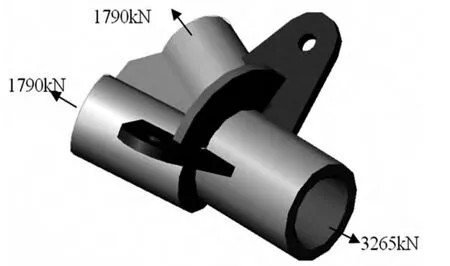
图8 节点受力计算示意图

图9 节点Von-mises应力云图(单位Pa)
从图9中可以看出,节点的最大Von-Mises应力为189MPa,远小于铸钢材料的屈服强度。
2.3 单侧张拉法的屋面找形技术
单侧张拉法更易造成张弦梁结构的竖向不均匀起拱,同时构件(含索和节点)安装时容易产生索力松弛、张弦梁滑移等现象,导致屋面找形困难。经过研究决定:先利用有限元计算设计起拱高度值,再在张弦梁关键截面上布设监测点进行变形实时监测,然后将实测的变形值与设计的起拱高度值进行对比分析,最后根据需调整的张弦梁起拱高度值、利用有限元软件反算索力,从而确保屋面找形平顺。
2.3.1 有限元法计算张弦梁设计起拱高度
利用Madis软件建立张弦梁的三维有限元模型,输入预设的张拉力参数,计算(F-2/G)~(2/1-2/3)的起拱高度最大值如表1所示。

表1 张弦梁起拱高度最大值 单位:mm
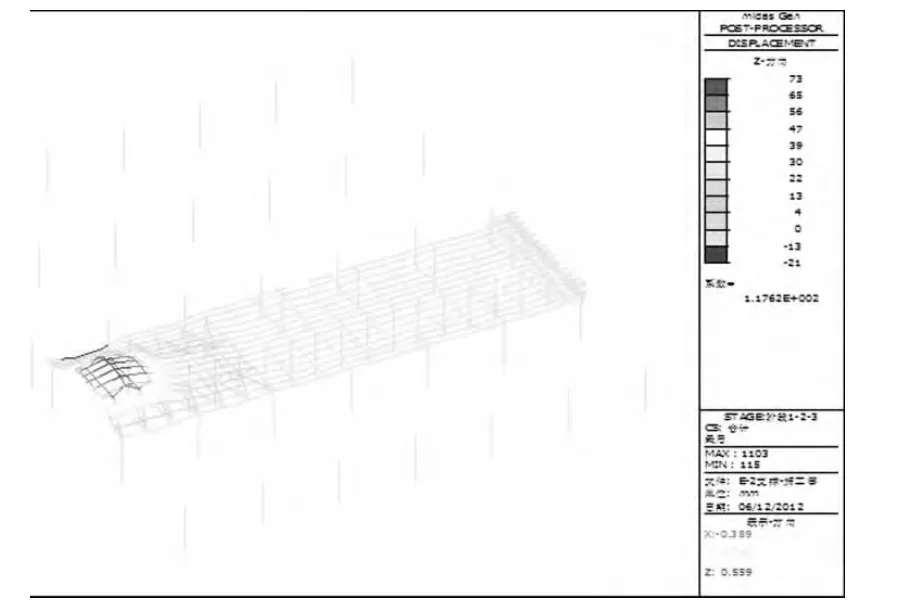
图10 1~6号索张拉至100%的竖向位移图
2.3.2 屋面变形的实时监测
建立张弦梁屋面变形的高程控制网,在每榀张弦梁的跨中截面贴莱卡60×60mm全站仪反射片,每次张拉结束后及时测量张弦梁起拱高度变化值。

图11 全站仪反射片布设现场照片
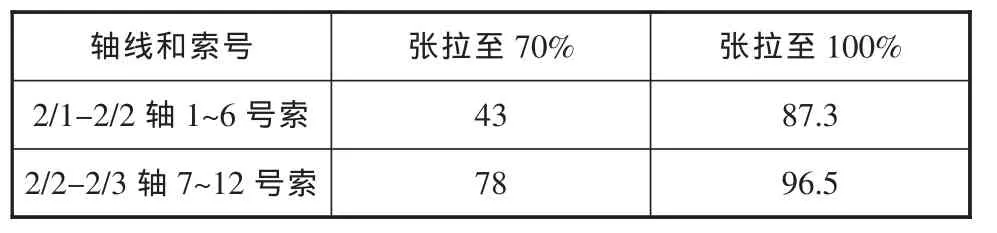
表2 实测起拱高度最大值 单位:mm
由表1和表2可知,张拉后的起拱高度值普遍偏大,起拱幅度无明显渐变规律,可见实际的张拉力偏大,需适当调整索力值。
2.3.3 索力调整控制屋面找形
鉴于前期监测的起拱值无渐变规律、难以实现屋面平顺效果,因此需根据既有起拱情况、再利用有限元软件反算索力、并实施监测实际索力值大小。由于本工程拉索为平行钢丝束,外包黑色HDPEHE和白色PE,无法直接在拉索上布置传感器来测试索力。因此,采用油压传感器直接得到施工阶段的索力,现将(F-2/G)~(2/1-2/3)区域索力调整后的实测值与设计值列表对比如下。
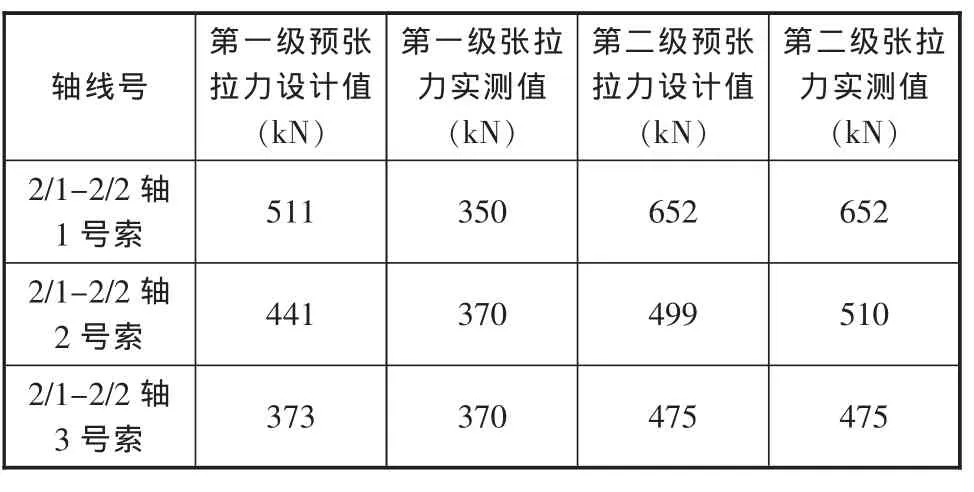
表3 索力实测值与设计值对比表
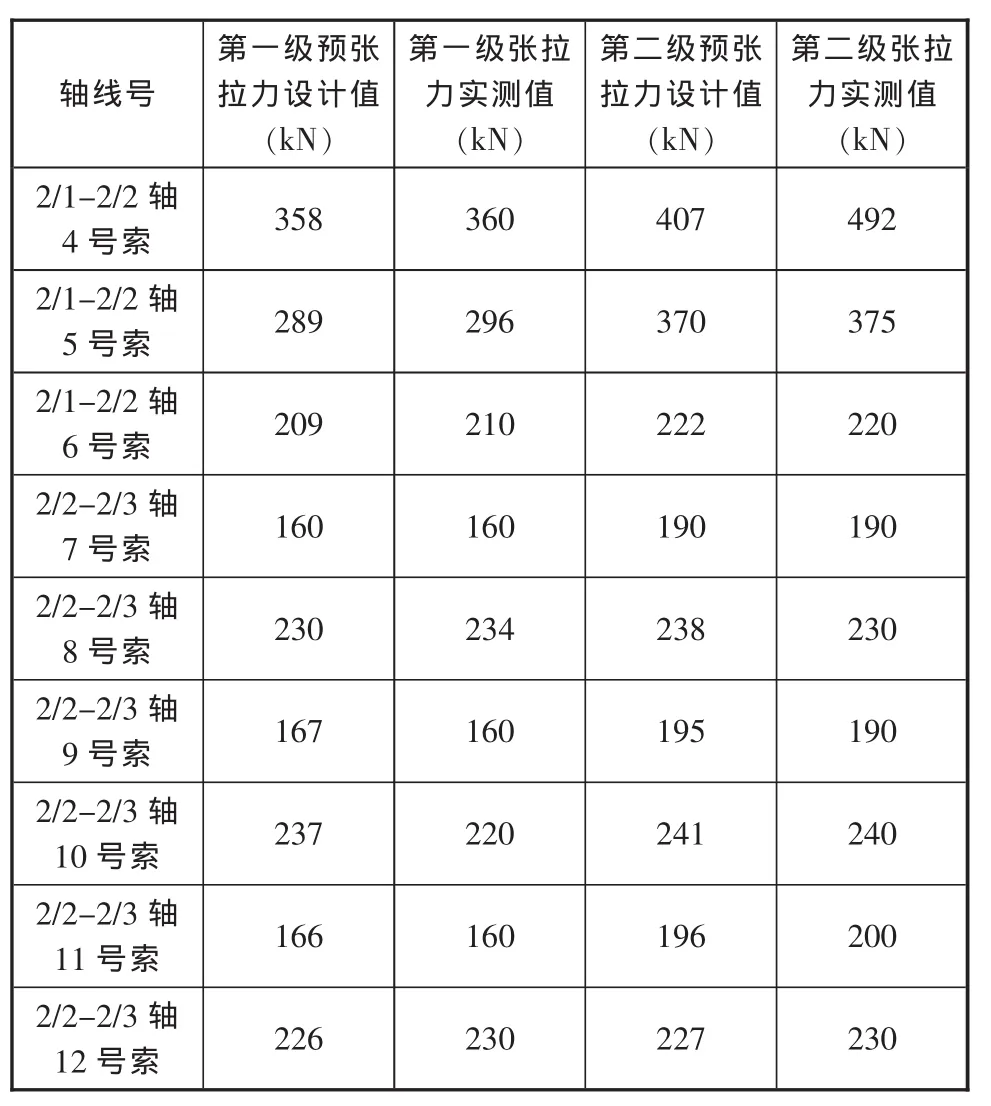

图12 索力调整现场照片
索力调整后,再次观测屋面变形得知,屋面起拱变形范围为±5mm,实现了既定的找形目标。
2.4 单侧张拉法的撑杆偏位控制
单侧张拉法易引起撑杆向一侧倾斜、从而造成索力出现明显的不对称性,如果偏差较大,将直接导致张拉失败。因此,对撑杆对称性的控制就显得至关重要。为了实时监测索力的对称特性,在固定端同榀张弦梁的两根分叉索上安装加速度传感器,通过JM5930动态信号采集系统直接采集张拉力达到 60%时的受迫振动频率,(F-2/G)~(2/1-2/2)拉索振动频率如表4所示。
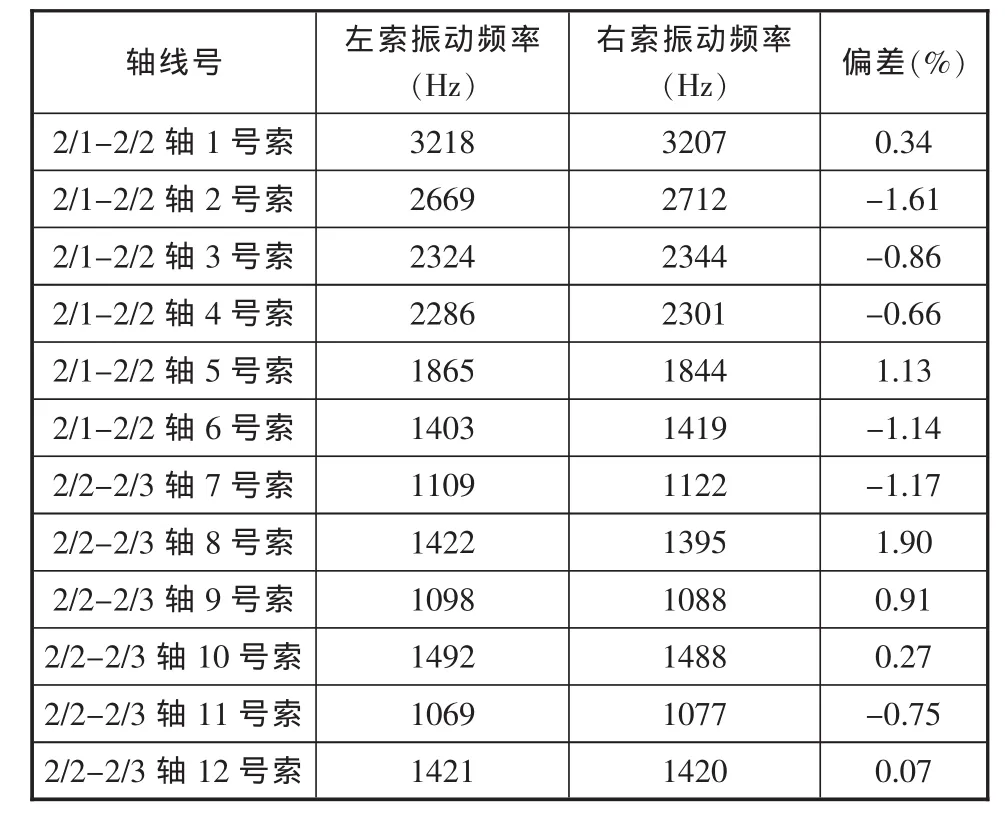
表4 拉索振动频率表
从表1中可以看出,同榀张弦梁左右两索的自振频率基本接近,说明分叉拉索的索力相同、撑杆的偏位值很小。
3 结束语
本工程采用单侧分级跳拉法张拉宁波铁路南站张弦梁雨棚结构,解决了撑杆下节点设计、撑杆偏位、屋面找形等关键技术,经过调整索力最终达到了预应力状态、实现了屋面结构精确找形。实践证明,单侧分级跳拉法能很好地适用既有线无站台柱大型张弦梁结构的张拉施工。
[1]陶长君,李维滨,仇荣根.呼和浩特新火车站预应力张弦梁施工技术[J].施工技术,2009,(7):36-39.
[2]张博浩,郭彦林,赵思远,等.张弦梁张拉过程平面外稳定性分析及施工方案比较[J].施工技术,2012,(14):49-54.
[3]齐永胜.张弦梁单侧和双侧预应力张拉效果的对比分析[J]. 常州工学院学报,2007,(1):25-28.
[4]王兆强.延安火车站钢结构雨篷张弦梁施工关键技术[J]. 施工技术,2008,(10):108-110.
[5]赵宪波,叶继红.张弦梁(桁架)结构的找形方法——分级卸载法[J].计算力学学报,2007,(6):846-851.
[6]赵宪忠,陈建兴,陈以一.张弦梁结构张拉过程中的结构性能试验研究[J].建筑结构学报,2007,(4):1-7.
