基于稀疏表示的相干分布式非圆信号的参数估计

2014-05-22杨学敏李广军

电子与信息学报 2014年1期

杨学敏李广军郑植

杨学敏*李广军郑植

(电子科技大学通信与信息工程学院成都 611731)

基于稀疏表示技术，该文提出一种相干分布式非圆信号的参数估计新方法。该方法将信号的非圆特性引入分布式信源模型，充分利用非圆信号的特性，联合阵列输出协方差矩阵和椭圆协方差矩阵，并将其矢量化之后表示在受制于稀疏限制的过完备字典上；然后将DOA估计转化为一个稀疏重构问题，能够一次性求解出中心DOA和角度扩展。仿真结果表明，该方法适用于各种非圆率的非圆信号，具有较好的信噪比性能和分辨力，所提出的方法还能对圆和非圆信号同时存在的情况进行有效估计。

信号处理；波达方向估计；相干分布式信号；非圆信号；角度扩展

1 引言

在军事、航天、声呐、雷达和通信等领域中，波达方向(DOA)估计问题在过去的几十年中得到了各国学者的广泛关注并有着极为重要的实际应用。由于实际情境中的环境比较复杂，分布式信源模型比点源更能满足DOA估计问题的需要，因此分布式信源的DOA估计研究近几年来引起了广大学者的浓厚兴趣。国内外学者提出了大量解决方法，但是这些方法都基于复圆信号特性的假设，这种假设能够简化计算，比如协方差匹配类算法[1]，基于传播算子方法的分布式信号参数估计算法[2,3]，最小方差波束形成器[4]等。然而，实际通信环境中存在着大量的非圆信号，如BPSK (Binary Phase Shift Keying), MSK (Minimum Shift Keying), GMSK (Guassian Minimum Shift Keying), PAM (Pulse-Amplitude Modulation)和UQPSK (Unbalanced Quadrature Phase Shift Keying)等。虽然非圆信号的引入会给DOA估计带来更大的复杂度，但利用信号的非圆特性可以获得更高的分辨力和信噪比性能，如NC- MUSIC (Non-Circular MUSIC)类算法[5,6]。另外，Gao等人[7]还提出了复圆与非圆信号同时存在情景下的DOA估计和识别方法。这些方法改善了复圆假设下的DOA估计性能，但都是基于点源模型情况下的研究，没有推广到分布式信源模型。为此，本文在分布式信源的模型中引入信号的非圆性质，对相干分布式非圆信号DOA估计问题进行研究。

本文基于稀疏表示方法提出一种非圆信号相干分布稀疏表示(Non-Circular Coherently Distri- buted Sparse Representation, NC-CDSR)的新算法，该算法充分利用协方差和椭圆协方差中的元素，增大观测数据量，从而达到更好的估计性能。所提方法不仅能同时获得中心DOA和角度扩展参数，还不需要任何谱峰搜索和特征值或奇异值分解，并且适用于复圆和非圆信号同时存在和低信噪比的情况。

2 信号模型

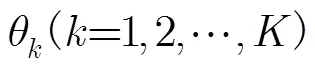
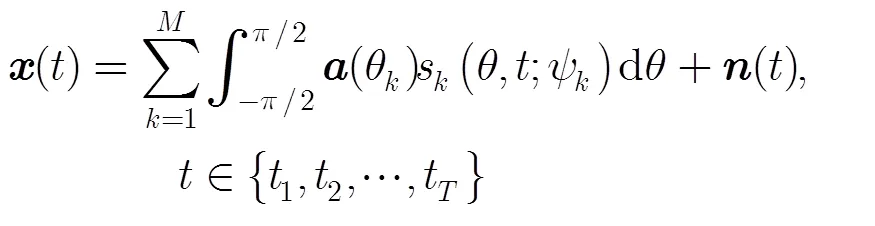
对于相干分布式非圆信号，角度信号密度可以表示为

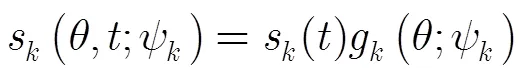
进一步地，有

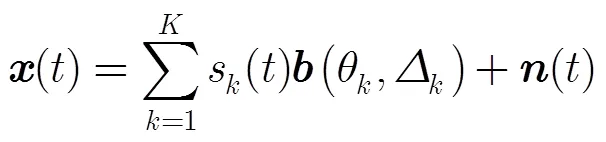
本文中以确定性角度信号密度服从高斯分布为例，有

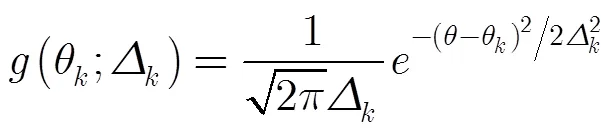
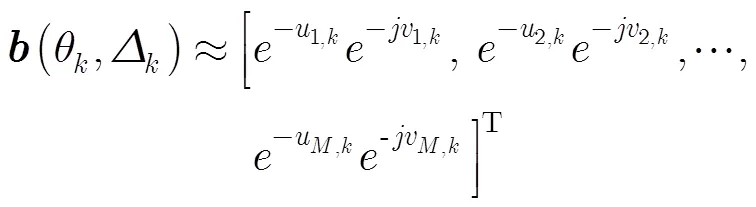
写成矩阵形式为

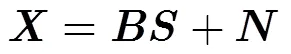
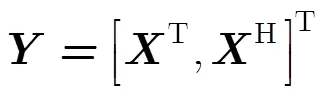
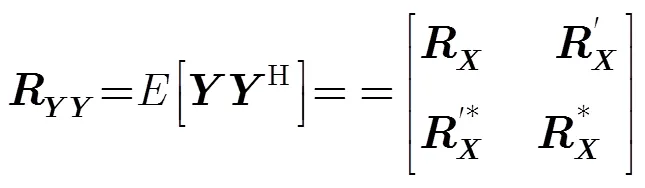
其中

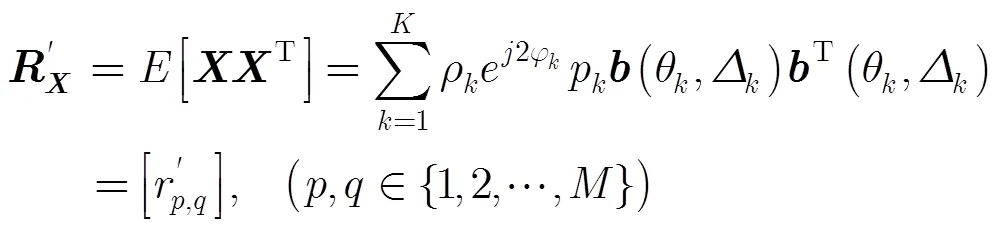
3 相干分布式非圆信号DOA估计算法

3.1 稀疏表示

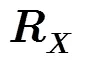
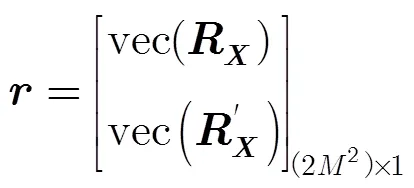
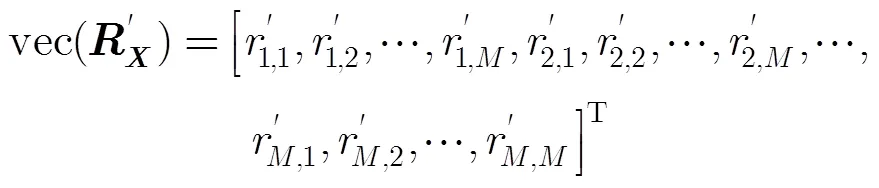
其中

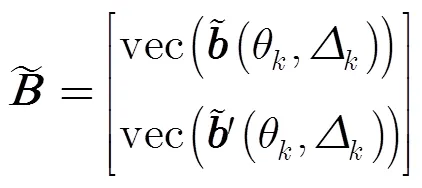
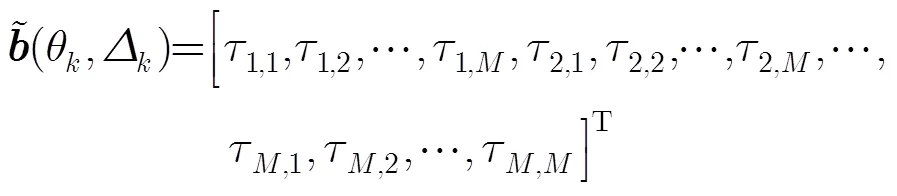
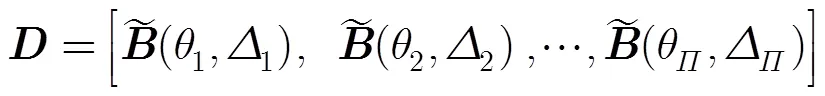
由式(9)可得相干分布式非圆信号DOA估计的稀疏模型。

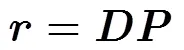
3.2 稀疏求解

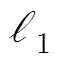
稀疏求解步骤如下：

3.3 算法复杂度分析

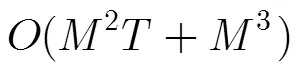
4 仿真结果及分析

本节实验中，天线阵列均采用8元均匀线阵。

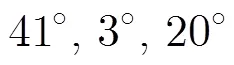
实验3考察快拍数对NC-CDSR, TLS- ESPRIT和DSPE方法估计性能的影响。信号源与实验1相同，在信噪比为10 dB的条件下，以不同的快拍数分别进行400次独立的Monte-Carlo仿真实验，得到图4所示的中心DOA估计的均方误差随快拍数变化的曲线。从图4可以看出，在快拍数很少的情况下，本文算法优于其它两种方法。

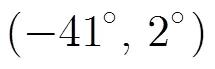
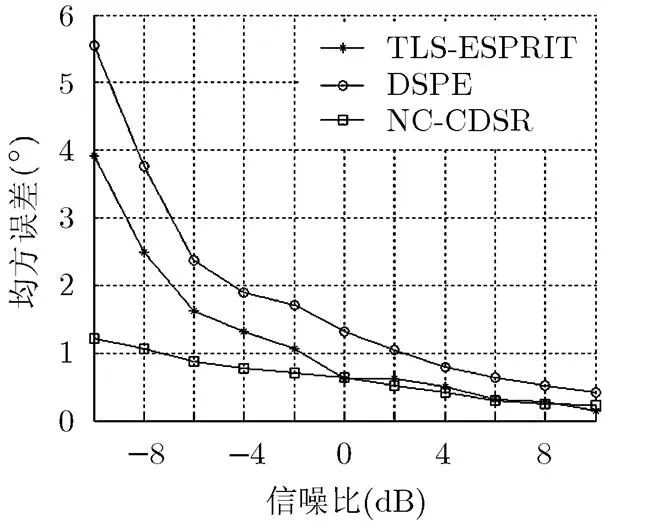
图1 3种算法中心DOA估计的均方误差随信噪比变化曲线

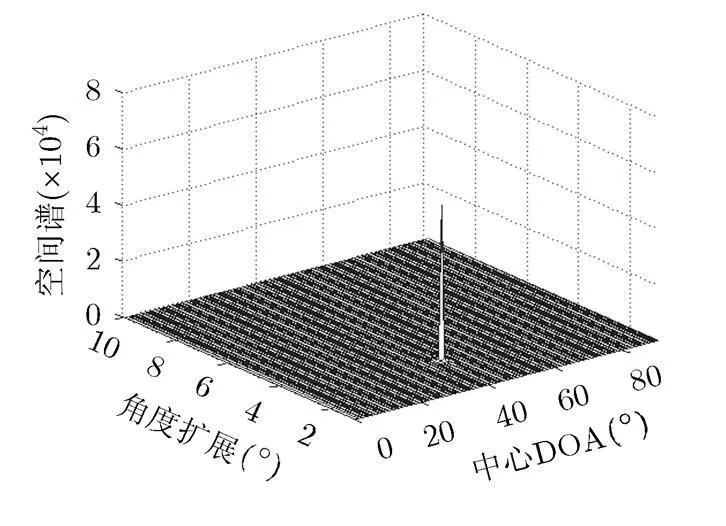
图2 信噪比为5 dB时的空间谱

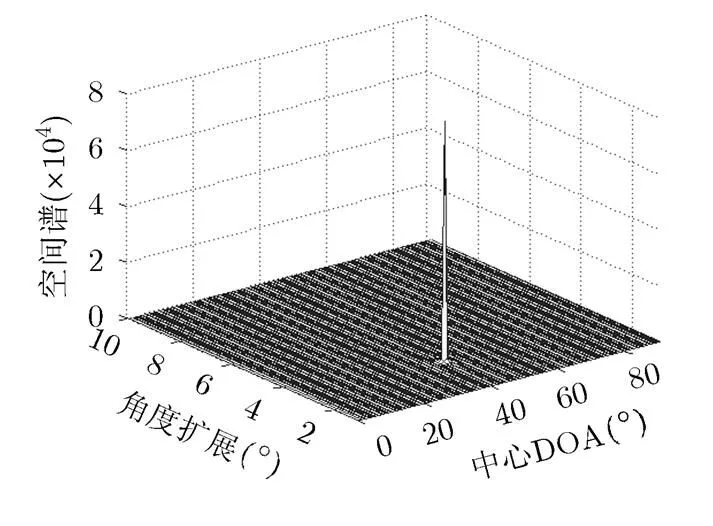
图3 信噪比为10 dB时的空间谱

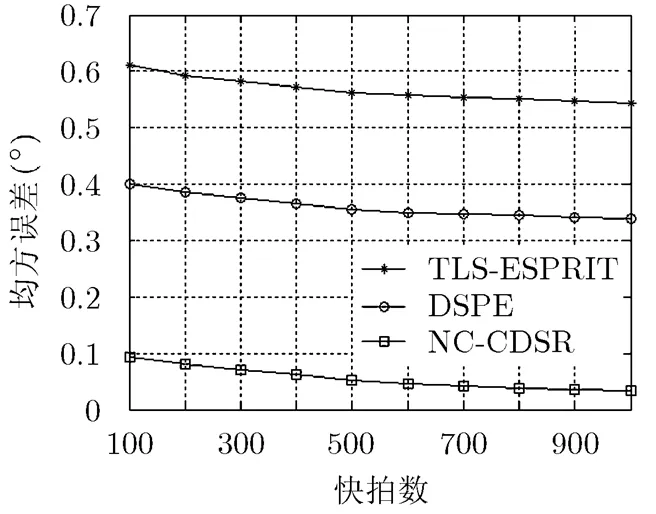
图4 3种算法中心DOA估计的均方误差随快拍数的变化曲线

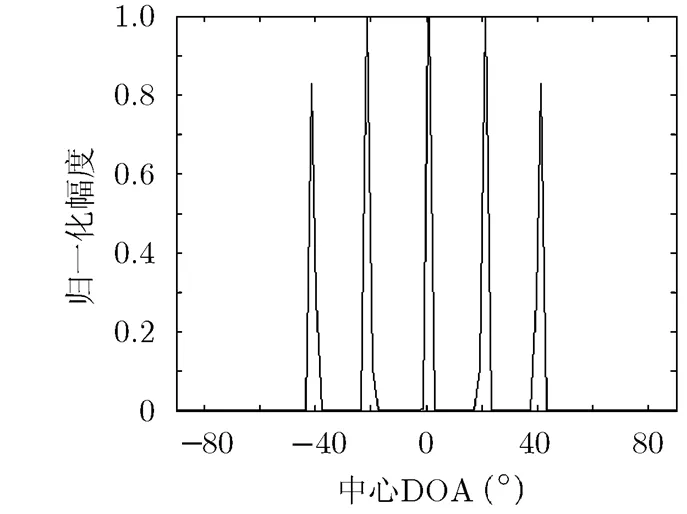
图5 圆信号和非圆信号同时存在的DOA估计

5 总结

本文提出了一种相干分布式非圆信号的DOA估计方法，该方法适用于各种非圆率的非圆信号。本文方法联合阵列输出协方差和椭圆协方差矩阵，利用稀疏表示技术建立过完备字典，采用StOMP算法对稀疏模型求解，能同时快速地获得中心DOA和角度扩展估计。仿真结果表明，本文方法具有很好的信噪比性能和分辨力，还能够对圆和非圆信号同时存在的情况进行有效估计。

[1] Zoubir A, Wang Y, and Chargé P. On the ambiguity of COMET-EXIP algorithm for estimating a scattered source[J]., 2006, 86(2): 733-743.

[2] Zheng Zhi, Li Guang-jun, and Teng Yun-long. Low-complexity 2D DOA estimator for multiple coherently distributed sources[J]., 2012, 31(2): 443-459.

[3] Zheng Zhi, Li Guang-jun, and Teng Yun-long. 2D DOA estimator for multiple coherently distributed sources using modified propagator[J]., 2012, 31(1): 255-270.

[4] Xu X. Spatially-spread sources and the SMVDR estimator[C]. 4th IEEE Workshop on Signal Processing Advances in Wireless Communications, Rome, Italy, 2003: 639-643.

[5] Gounon P, Adnet C, and Galy J. Localization angulaire de signaux non circulaires[J]., 1998, 15(1): 17-23.

[6] Abeida H and Delmas J. MUSIC-like estimation of direction of arrival for noncircular sources[J]., 2006, 54(7): 2678-2690.

[7] Gao F, Wang Y, and Nallanathan A. Improved MUSIC by exploiting both real and complex sources[C]. MILCOM: IEEE Military Communications Conference, Washington DC, USA, 2006: 1-6.

[8] Malioutov D, Cetin M, and Willsky A. A sparse signal reconstruction perspective for source localization with sensor arrays[J]., 2005, 53(8): 3010-3022.

[10] Guo X, Wan Q, Wu B,.. Parameters localization of coherently distributed sources based on sparse signal representation[J]., 2007, 1(4): 261-265.

[11] He Z, Liu Q, Jin L,..Low complexity method for DOA estimation using array covariance matrix sparse representation[J]., 2013, 49(3): 228-230.

[12] Liu Z and Huang Z. Direction-of-arrival estimation of noncircular signals via sparse representation[J]., 2012, 48(3): 2690-2698.

[13] 韩英华, 汪晋宽, 宋昕. 相干分布式信源二维波达方向估计算法[J]. 电子与信息学报, 2009, 31(2): 323-326.

Han Ying-hua, Wang Jin-kuan, and Song Xin. 2D DOA estimation algorithm for coherently distributed source[J].&, 2009, 31(2): 323-326.

[15] Donoho D L, Tsaig Y, Drori I,.. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]., 2012, 58(2): 1094-1121.

[16] Valaee S, Champagne B, and Kabal P. Parametric localization of distributed sources[J]., 1995, 43(9): 2144-2153.

[17] Zheng Zhi, Li Guang-jun, and Teng Yun-long. Simplified estimation of 2D DOA for coherently distributed sources[J]., 2012, 62(4): 907-922.

杨学敏：男，1986年生，博士生，研究方向为阵列信号处理中的方向估计.

李广军：男，1950年生，教授，博士生导师，研究方向为通信系统设计及通信中的信号处理等.

郑植：男，1980年生，助理研究员，研究方向为阵列信号处理中的分布源参数估计.

Parameters Estimation of Coherently Distributed Non-circular Signal Based on Sparse Representation

Yang Xue-min Li Guang-jun Zheng Zhi

(,611731,)

A novel method for parameters estimation of coherently distributed non-circular signal based on the concept of sparse representation is proposed. The non-circular property is introduced into the model of distributed source, and the non-circular property is fully used to unite the covariance and elliptic covariance matrix of the array output. By representing them on overcomplete dictionaries subject to sparse constraint, and transforming DOA estimation into a sparse reconstruction problem, the method is able to solve the central DOA and angular spread at a time. Simulation results show that the proposed method can be used in different kinds of non-circular rate with better performance of low SNR and resolution, and the proposed algorithm can also effectively estimate the DOA in the case of both circular and non-circular signal existing.

Signal processing; DOA estimation; Coherently distributed signal; Non-circular signal; Angular spread

TN911.7

1009-5896(2014)01-0164-05

10.3724/SP.J.1146.2013.00444

2013-04-07收到，2013-07-18改回

国家自然科学基金(61301155, 61176025)资助课题

杨学敏 yxm.uestc@gmail.com