认知WSN中基于能量有效性自适应观测的梯度投影稀疏重构方法

2014-05-22许晓荣姚英彪包建荣

电子与信息学报 2014年1期

许晓荣姚英彪包建荣陆宇

许晓荣*姚英彪包建荣陆宇

(杭州电子科技大学通信工程学院杭州 310018)

针对认知无线传感器网络中传感器节点侧的模拟信息转换器对本地感知数据进行稀疏表示与压缩测量，该文提出一种基于能量有效性观测的梯度投影稀疏重构(GPSR)方法。该方法根据事件区域内认知节点对实际感知到的非平稳信号空时相关性结构，映射到小波正交基级联字典进行稀疏变换，通过加权能量子集函数进行自适应观测，以能量有效的方式获取合适的观测值，同时对所选观测向量进行正交化构造测量矩阵。汇聚节点采用GPSR算法进行自适应压缩重构。仿真比较了GPSR自适应重构与正交匹配追踪(OMP)重构算法。仿真结果表明，在压缩比小于0.2的区域内，基于能量有效性观测的GPSR自适应重构效果优于传统随机高斯测量信号重构。在相同节点数情况下，GPSR自适应压缩重构方法在低信噪比区域内具有较小的重构均方误差，且该方法所需观测数明显低于随机高斯观测，同时有效保障了感知节点的能耗均衡。

认知无线传感器网络；能量有效性；梯度投影稀疏重构；自适应压缩；加权能量子集函数

1 引言

认知无线传感器网络(C-WSN)中包含大量具有认知功能的传感器节点，节点能耗受限且数量众多，多节点通过分布式组网对周围环境中特定的参数信息进行感知、传输和处理[1,2]。在C-WSN中，节点机会地利用主用户(Primary User, PU)频谱将本地感知信息发送到汇聚节点(sink)进行数据融合，汇聚节点对多个认知节点的感知信息进行重构[3]。在对同一目标进行感知的过程中，节点在感知时间和空间位置上均存在着相关性[4]。利用感知数据的时空相关性，通过设计满足约束等距性质(Restricted Isometry Property, RIP)的自适应观测矩阵，使得变换域稀疏的可压缩信号在观测过程中不发生信息丢失且能够以高概率实现稀疏重构，是压缩感知(Compressed Sensing, CS)在C-WSN应用中亟待解决的问题。此外，由于WSN节点能耗受限，必须考虑在保障节点能量有效性条件下的自适应压缩重构[1,5]。

本文在上述文献WSN中基于CS理论进行感知信号稀疏重构与节点能耗分析的基础上，根据认知节点对实际感知到的非平稳信号空时相关性结构，感知数据首先映射到Daubechies系列小波正交基(db2和db4)级联字典进行稀疏变换[15]，通过选择变换域观测向量，以能量有效的方式获取合适的观测值，同时对所选观测向量进行正交化构造测量矩阵。小波正交基级联字典稀疏变换矩阵与构造的观测矩阵之间满足RIP条件[15]，以此得到基于能量有效性的自适应观测向量，感知节点侧的模拟信息转换器(Analog-to-Information Converter, AIC)将经自相关运算后的观测向量发送至汇聚节点，采用GPSR凸松弛法进行信号重构，形成自适应压缩。

2 基于能量有效性的自适应观测

2.1 C-WSN测量矩阵设计准则

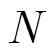
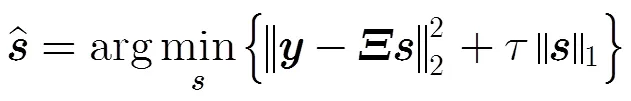
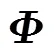
不同于传统随机高斯或贝努利观测的随机信号压缩，在本文场景中，需要设计满足RIP条件且具有较低观测次数的自适应观测矩阵对节点实际感知到的非平稳信号进行自适应观测，同时兼顾C-WSN节点的能量有效性。文献[16]已经证明了基于变换域最大能量子集构造的自适应观测矩阵与稀疏变换基矩阵不相关，即满足RIP性质。本文在文献[16]的基础上，根据各节点感知时的能耗，构造加权的变换域稀疏信号能量子集函数，以获得最大加权能量子集，并进行正交化处理，形成保障节点能量有效性的自适应观测。同时，汇聚节点采用GPSR算法进行自适应压缩重构。

2.2 基于最大加权能量子集的自适应观测

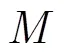
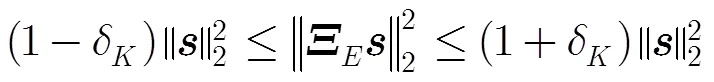
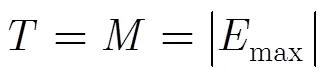
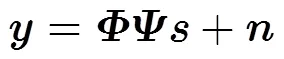
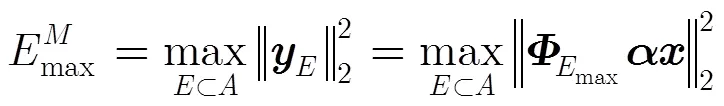
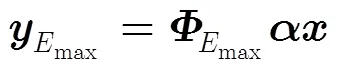
图1给出了C-WSN中基于能量有效性观测的GPSR压缩重构流程图。

3 汇聚节点GPSR压缩重构

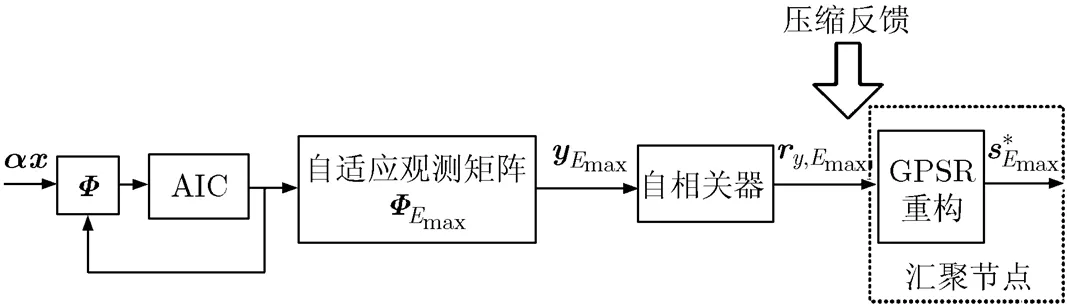
图1 C-WSN中基于能量有效性观测的GPSR压缩重构流程图

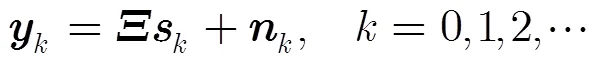
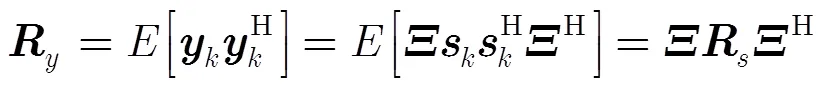
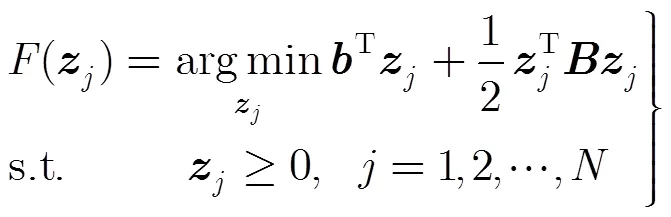
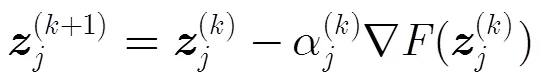
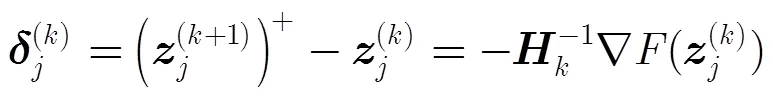
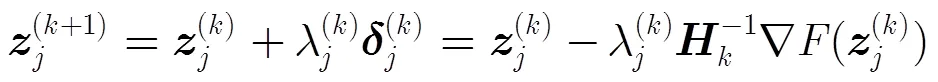
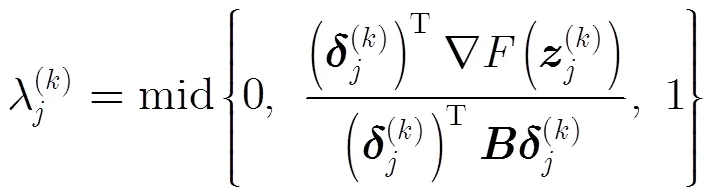
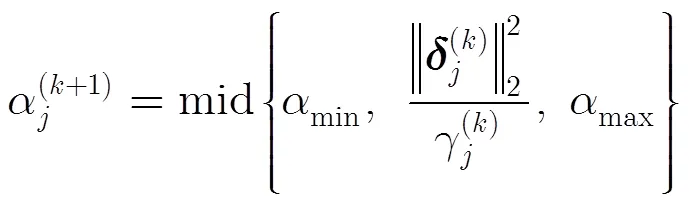
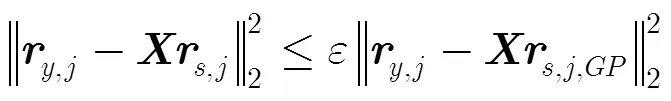
4 仿真与性能分析

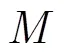
图4比较了不同信噪比时基于能量有效性观测自适应压缩反馈GPSR与随机压缩反馈GPSR的重构MSE性能。为获得较低的均方误差，取仿真节点数为60。由图可知，相同压缩反馈GPSR算法随着SNR的提高，重构MSE将显著降低，如当SNR为10 dB时，随着压缩比的增加，自适应压缩反馈GPSR算法的重构MSE可达-6 dB，但波动较大。在低SNR情况下，算法的重构MSE较为平稳。此外，低SNR情况下的自适应压缩反馈GPSR重构MSE性能优于随机压缩反馈，如当SNR为0 dB时，自适应压缩反馈GPSR重构MSE优于随机压缩反馈约1 dB，收敛时重构MSE达到-3.5 dB，且重构MSE随压缩比的变化并不明显。当SNR为10 dB时，随机压缩反馈GPSR重构MSE迅速下降至-10 dB，明显优于自适应压缩反馈GPSR。因此，基于能量有效性观测的自适应压缩反馈GPSR在低信噪比区域具有一定的优势，可应用于实际C-WSN低信噪比场景中。

图2 不同节点数情况下OMP与GPSR- BB两种重构方法的重构均方误差性能

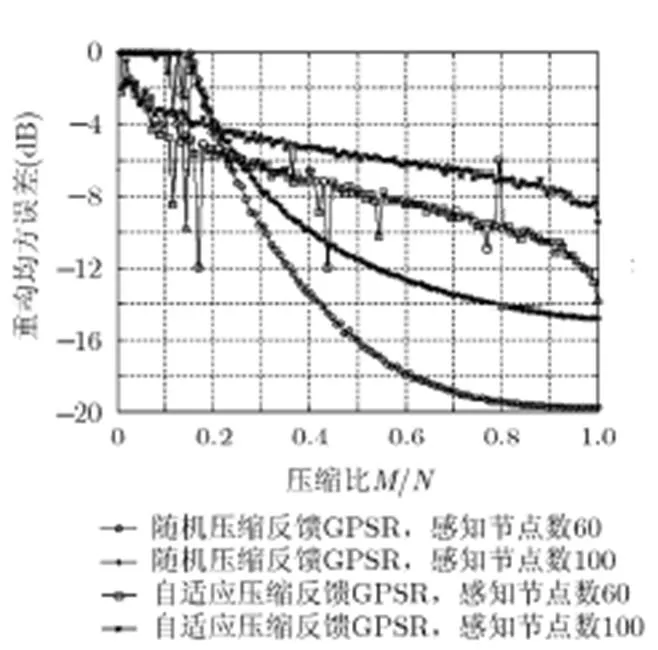
图3 不同节点数时自适应压缩反馈与随机压缩反馈重构均方误差

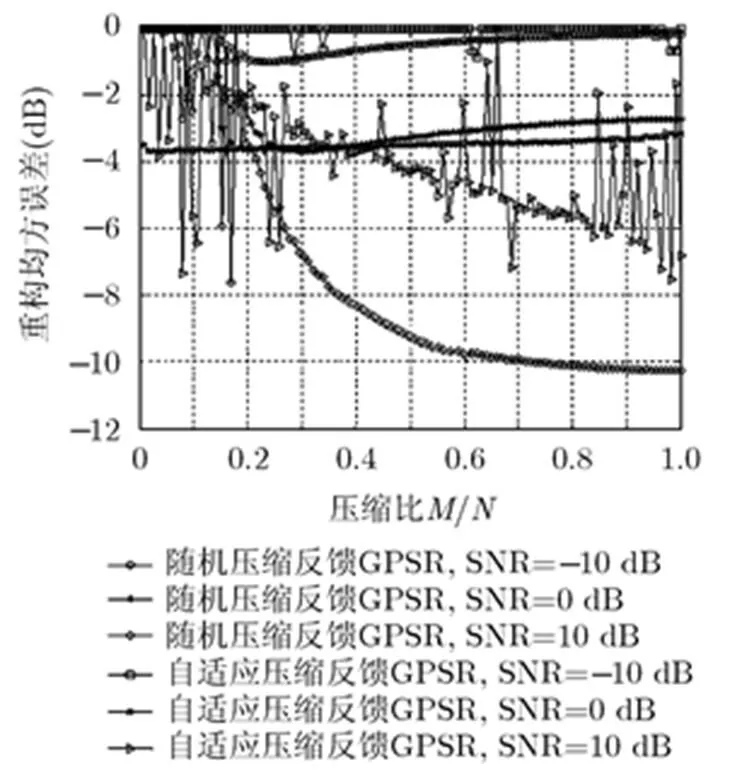
图4 不同信噪比时自适应压缩反馈与随机压缩反馈重构均方误差

5 结束语

在C-WSN中，传统压缩反馈机制中采用的测量矩阵为随机高斯或贝努利测量矩阵，其元素取值具有随机性，即不具备自适应特性。针对C-WSN中感知信号的时空相关性特点，论文提出了一种基于能量有效性观测的自适应压缩反馈梯度投影稀疏重构(GPSR)方法。该方法以节点接收能耗作为权值，将加权感知信号通过AIC进行稀疏表示与压缩测量，加权感知向量经正交小波基级联字典稀疏变换后能量守恒，即以能量有效的方式构造自适应测量矩阵，形成自适应压缩反馈。汇聚节点采用GPSR-BB凸优化算法重构感知信号的自相关向量，以此获得重构的加权感知向量。仿真结果表明，在相同重构均方误差要求下，GPSR-BB算法重构信号所需的观测值小于传统OMP贪婪算法所需观测值。基于能量有效性观测的GPSR自适应压缩重构在低压缩比和低信噪比情况下的收敛特性均优于随机高斯观测GPSR重构，该方法在低压缩比和低信噪比区域内可实现感知信号的快速重构，同时有效保障了感知节点的能耗均衡。

[1] 唐亮, 周正, 石磊, 等. 基于能量均衡的无线传感器网络压缩感知算法[J]. 电子与信息学报, 2011, 33(8): 1919-1923.

Tang Liang, Zhou Zheng, Shi Lei,.. Energy balance based WSN compressive sensing algorithm[J].&, 2011, 33(8): 1919-1923.

[2] Yang A Y, Gastpar M, Bajcsy R,.. Distributed sensor perception via sparse representation[J]., 2010, 98(6): 1077-1088.

[3] Dyonisius D A and Geert L. Compressive wideband power spectrum estimation[J]., 2012, 60(9): 4775-4789.

[4] Tsung H Y, Oussama S, Santiago R P,.. A wideband spectrum sensing processor with adaptive detection threshold and sensing time[J]., 2011, 58(11): 2765-2775.

[5] 唐亮. 压缩感知及其在超宽带无线传感器网络中的应用研究[D]. [博士论文], 北京邮电大学, 2011: 80-95.

Tang Liang. The research of compressive sensing and its application in UWB and wireless sensor networks[D]. [Ph.D. dissertation], Beijing University of Posts and Telecommunications, 2011: 80-95.

[6] 吴大鹏, 孙青文, 唐季超, 等. 能量有效的无线传感器网络协作压缩感知机制[J]. 电子与信息学报, 2012, 34(11): 2687-2693.

Wu Da-peng, Sun Qing-wen, Tang Ji-chao,.. Energy efficient cooperative compressive sensing mechanism in wireless sensor networks[J].&, 2012, 34(11): 2687-2693.

[7] Peyre G. Best basis compressed sensing[J]., 2010, 58(5): 2613-2622.

[8] 焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651-1662.

Jiao Li-cheng, Yang Shu-yuan, Liu Fang,.. Development and prospect of compressed sensing[J]., 2011, 39(7): 1651-1662.

[9] 李小波. 基于压缩感知的测量矩阵研究[D]. [硕士论文], 北京交通大学, 2010: 2-6, 9-16, 22-24.

Li Xiao-bo. Research on measurement matrix based on compressed sensing[D]. [Master dissertation], Beijing Jiaotong University, 2010: 2-6, 9-16, 22-24.

[10] 杨海蓉, 张成, 丁大为, 等. 压缩传感理论与重构算法[J]. 电子学报, 2011, 39(1): 142-148.

Yang Hai-rong, Zhang Cheng, Ding Da-wei,.. The theory of compressed sensing and reconstruction algorithm[J]., 2011, 39(1): 142-148.

[11] 刘亚新, 赵瑞珍, 胡绍海, 等. 用于压缩感知信号重建的正则化自适应匹配追踪算法[J]. 电子与信息学报, 2010, 32(11): 2713-2717.

Liu Ya-xin, Zhao Rui-zhen, Hu Shao-hai,.. Regularized adaptive matching pursuit algorithm for signal reconstruction based on compressive sensing[J].&, 2010, 32(11): 2713-2717.

[12] 叶蕾, 杨震, 王天荆, 等. 行阶梯观测矩阵、对偶仿射尺度内点重构算法下的语音压缩感知[J]. 电子学报, 2012, 40(3): 429-434.

Ye Lei, Yang Zhen, Wang Tian-jing,.. Compressed sensing of speech signal based on row echelon measurement matrix and dual affine scaling interior point reconstruction method[J]., 2012, 40(3): 429-434.

[13] Figueiredo M A T, Nowak R D, and Wright S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J]., 2007, 1(4): 586-597.

[14] Wright S J, Nowark R D, and Figueiredo M A T. Sparse reconstruction by separable approximation[J]., 2009, 57(7): 2479-2493.

[15] Elad M. Optimized projections for compressed sensing[J]., 2007, 55(12): 5695-5702.

[16] Xu Xiao-rong, Zhang Jian-wu, Huang Ai-ping,.. An adaptive measurement scheme based on compressed sensing for wideband spectrum detection in cognitive WSN[J].(), 2012, 29(6): 585-592.

[17] 江若宜, 季薇, 郑宝玉. 无线传感器网络中协作通信的能耗优化方法研究[J]. 电子与信息学报, 2010, 32(6): 1475-1479.

Jiang Ruo-yi, Ji Wei, and Zheng Bao-yu. Joint optimization of energy consumption in cooperative wireless sensor networks[J].&, 2010, 32(6): 1475-1479.

[18] Tan L T, Kong H Y, and Bao V N Q. Projected Barzilai-Borwein methods applied to distributed compressive spectrum sensing[C]. IEEE International Symposia on New Frontiers in Dynamic Spectrum Access Networks (IEEE DySPAN), Singapore, 2010: 1-7.

[19] 邓军. 基于凸优化的压缩感知信号恢复算法研究[D]. [硕士论文], 哈尔滨工业大学, 2011: 20-37.

Deng Jun. Research on compressive sensing signal reconstruction by convex optimization[D]. [Master dissertation], Harbin Institute of Technology, 2011: 20-37.

许晓荣：男，1982年生，讲师，博士，研究方向为认知无线网络、压缩感知、无线传感器网络等.

姚英彪：男，1976年生，副教授，博士，研究方向为无线传感器网络等.

包建荣：男，1978年生，副教授，博士，研究方向为压缩感知、深空通信信道编码理论等.

陆宇：男，1977年生，讲师，博士，研究方向为压缩感知、非线性优化理论等.

Gradient Projection Sparse Reconstruction Approach Based on Adaptive Energy-efficiency Measurement in Cognitive WSN

Xu Xiao-rong Yao Ying-biao Bao Jian-rong Lu Yu

(,,310018,)

Cognitive sensor local information sparse representation and compressive measurement are investigated, which are conducted by Analog-to-Information Converters (AIC) at each sensor in Cognitive Wireless Sensor Networks (C-WSN). Gradient Projection Sparse Reconstruction (GPSR) scheme based on energy-efficiency measurement is proposed. According to the spatial-temporal correlation structure of non-stationary signals perceived by massive cognitive sensors in Event Region (ER), these signals are mapped to wavelet orthogonal basis concatenate dictionaries to perform sparse representation. Adaptive measurement is implemented via weighted energy subset function, which could obtain the proper observation in energy-efficiency approach. The corresponding measurement matrix is constructed by the orthogonalization of these selected measurement vectors. Adaptive compressive reconstruction is performed at sink via GPSR algorithm, which is compared with conventional Orthogonal Matching Pursuit (OMP) algorithm. Simulation results indicate that, signal reconstruction effect based on energy-efficiency measurement GPSR adaptive compression is superior to Gaussian random measurement in the region where compression ratio is less than 0.2. With the same sensor numbers, the proposed GPSR adaptive compression approach has small reconstruction Mean Square Error (MSE) at low Signal-to-Noise Ratio (SNR) region, and the required measurement number is less than Gaussian random measurement, which guarantees sensors’ energy balance effectively.

Cognitive Wireless Sensor Networks (C-WSN); Energy-efficiency; Gradient Projection Sparse Reconstruction (GPSR); Adaptive compression; Weighted energy subset function

TP393

1009-5896(2014)01-0027-07

10.3724/SP.J.1146.2013.00392

2013-03-28收到，2013-07-27改回

国家自然科学基金(61102066, 61100044, 61001133)和浙江省自然科学基金(LY12F01007)资助课题

许晓荣 xuxr@hdu.edu.cn