基于扩维的多通道联合频率和到达角估计

赵 曼 陈 辉



基于扩维的多通道联合频率和到达角估计

赵 曼 陈 辉*

(空军预警学院重点实验室 武汉 430019)

针对宽频段信号的时空欠采样问题，该文提出基于扩维的多通道联合频率和到达角估计方法。在时间和空间均欠采样的情况下，该方法实现了频率和到达角的2维无模糊估计。通过构造空时2维无模糊阵列结构，将多个采样通道联合扩维，解决了时间欠采样问题；将多个快拍通道联合扩维，克服了空间欠采样问题。同时，为了降低运算量，利用时域滤波技术，将频率和到达角估计进行时空级联，得到了自动配对的频率和到达角无模糊估计值，且避免了高维特征值分解和2维谱峰搜索，减少了运算量。仿真结果验证了该方法的有效性。

阵列信号处理；时空欠采样；空时2维无模糊阵列；多通道联合；频率估计；到达角估计

1 引言

近年来，频率和到达角估计一直是阵列信号处理领域的一个研究热点，它被广泛应用于雷达、通信、声呐等方面。学者们已经提出大量频率和到达角估计的有效方法。文献[1]提出了最大似然的频率和到达角估计算法，该方法通过多维搜索求解，具有最优的估计性能。文献[2]利用两个1维的旋转不变技术(Estimation of Signal Parameters via Rotational Invariance Technique, ESPRIT)分别估计频率和到达角，估计值通过标记子空间方案配对。文献[3]将传统的1维多重信号分类(MUltiple SIgnal Classification, MUSIC)推广到2维MUSIC，利用高维特征值分解和2维搜索实现了频率和到达角估计。文献[4]提出一种树结构的频-空-频多重信号分类(Frequency-Space-Frequency MUSIC, FSF MUSIC)算法，利用一定量的1维搜索分别得到频率和到达角，估计值自动配对，无需高维特征值分解，精度较高。已有这些算法均在满足时空采样定理的条件下进行研究。

为了解决宽频段信号的时空欠采样问题，本文提出了基于扩维的多通道联合频率和到达角估计方法。该方法通过构造空时2维无模糊阵列结构，在时间和空间均欠采样的情况下，实现了频率和到达角的2维无模糊估计。同时，为了降低运算量，将频率估计和到达角估计进行时空级联，得到了自动配对的频率和到达角无模糊估计值，且避免了高维特征值分解和2维搜索，增强了实用性。计算机仿真验证了算法的有效性。

2 传统空时2维阵列模型

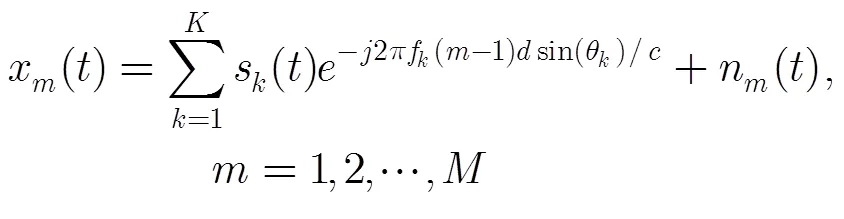
式中

(1)时间欠采样问题：考虑到当前的硬件工艺水平，实现宽频段信号的Nyquist采样，代价相当高，且ADC和DSP之间存在严重的工作速率瓶颈问题，因此需要进行时间欠采样，但此时会发生频谱混叠，频率估计发生模糊。

(2)空间欠采样问题：对于宽频段信号的DOA估计，以高频端半波长设计阵列，导致阵元在物理安置的困难和低频段阵元耦合的严重加剧，同时造成估计精度和分辨力下降，以低频段半波长设计阵列，在高频端出现估计模糊。

3 空时2维无模糊阵列模型

4 基于扩维的多通道联合频率和到达角估计

基于空时2维无模糊阵列结构，提出了基于扩维的多通道联合频率和到达角估计方法，该方法利用多采样通道联合进行频率估计，解决了时间欠采样问题；利用多快拍通道联合进行到达角估计，克服了空间欠采样问题；利用时域滤波技术[4]，将频率和到达角估计进行时空级联，得到了自动配对的频率和到达角无模糊估计值。

图1 阵元多采样通道接收模型

图2 多快拍通道阵列结构

4.1 多采样通道联合频率估计

定义时域协方差矩阵为

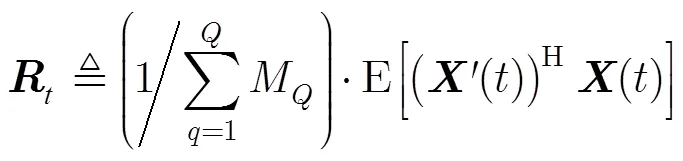
则

式中

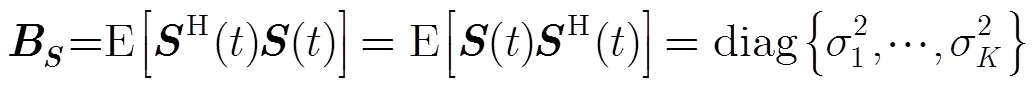
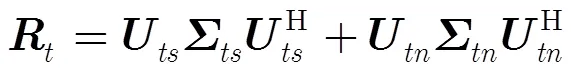
根据子空间的正交性得，多采样通道联合频率估计的MUSIC算法公式[6]为

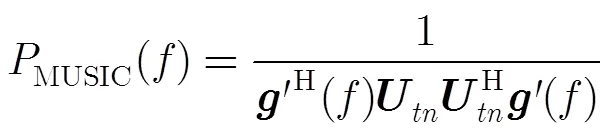
4.2 多快拍通道联合到达角估计

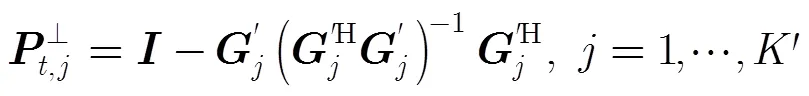
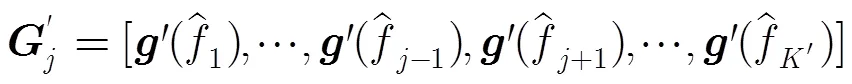
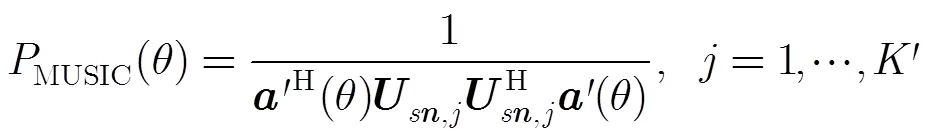
4.3 采样频率和阵元间距的选择

从时域流型矩阵分析可知，频率估计模糊的原因在于同一时域导向矢量可能有不同的频率与之对应，即导向矢量满足关系：

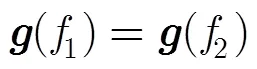
同理，到达角估计模糊的原因为同一空域导向矢量可能有不同的到达角与之对应，即导向矢量满足：

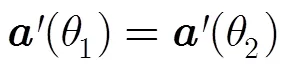
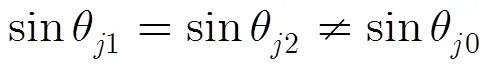
又由式(18)可得

因此，只要存在两个子阵使整个频段的最小波长满足式(20)，便可实现整个频段到达角的无模糊估计。

5 仿真分析

图3给出了信噪比为0 dB的多通道联合频率估计结果，图4(a)和图4(b)给出了对应频率的到达角估计结果。从图3和图4可以看出，多通道联合频率和到达角估计方法可以实现时空欠采样下的频率和到达角2维估计，其中多采样通道联合解决了时间欠采样问题，多快拍通道联合克服了空间欠采样。

6 结论

针对宽频段信号的时空欠采样问题，本文提出了基于扩维的多通道联合频率和到达角估计方法。该方法通过构造空时2维无模糊阵列结构，解决了时间欠采样的频率模糊问题和空间欠采样的到达角模糊问题。其中，将多个采样通道进行联合扩维处理，利用时域多采样通道联合导向矢量进行谱峰搜索，解决了时间欠采样的频率模糊问题，将多个快拍通道联合扩维处理，利用空域多快拍通道联合导向矢量进行谱峰搜索，解决了空间欠采样的到达角模糊问题。同时，为了降低运算量，该方法利用时域滤波技术，将频率估计和到达角估计进行时空级联，在时间和空间均欠采样的情况下，得到了自动配对的频率和到达角无模糊估计值，且避免了高维特征值分解和2维搜索，增强了实用性。计算机仿真验证了算法的有效性。

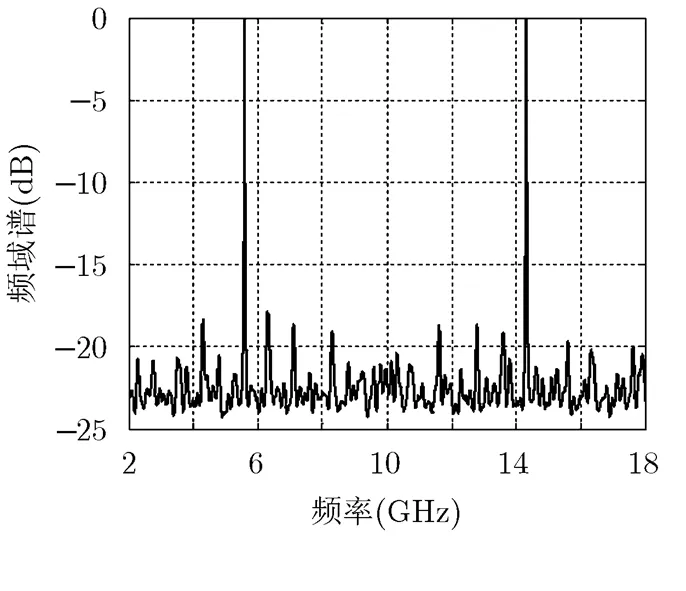
图3频率估计结果

图4到达角估计结果

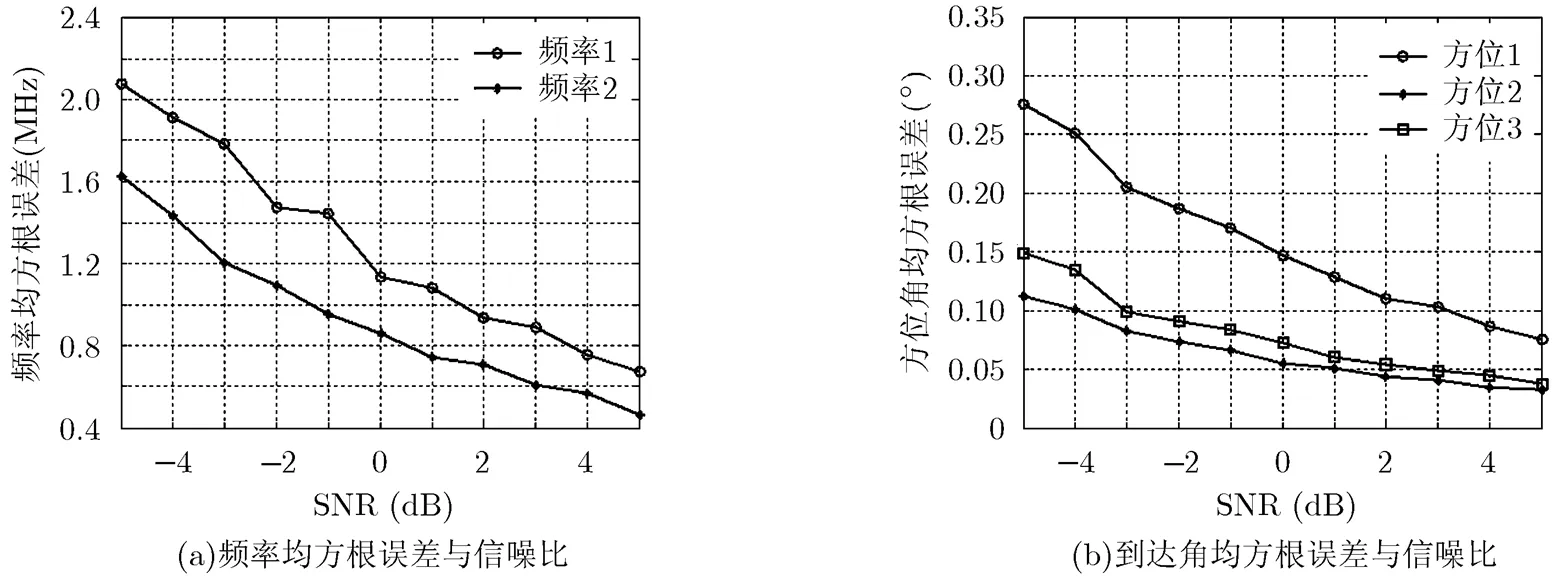
图5频率和到达角均方根误差与信噪比的关系

[1] Atheley F. Asymptotically decoupled angle-frequency estimation with sensor arrays[C]. IEEE Signals, Systems, and Computer, Pacific Grove, CA, USA, 1999: 1098-1102.

[2] Chen Y H and Chen C H. Direction-of-arrival and frequency estimations for narrowband sources using two single rotation invariance algorithms with the marked subspace[J]., 1992, 139(4): 297-300.

[3] Wang S, Caffery J, and Zhou X. Analysis of a joint space-time DOA/FOA estimator using MUSIC[C]. IEEE International Symposium on PIMRC, San Diego, 2001: 138-142.

[4] Lin J D, Fang W H, Wang Y Y,.. FSF MUSIC for joint DOA and frequency estimation and its performance analysis[J]., 2006, 54(12): 4529-4542.

[5] Zoltowski M D and Mathews C P. Real-time frequency and 2-D angle estimation with sub-Nyquist spatio-temporal sampling[J]., 1994, 42(10): 2781-2797.

[6] 王鑫, 赵春晖, 戎建刚.多路延迟结构的修正MUSIC算法频率估计[J]. 系统工程与电子技术, 2009, 31(4): 795-798.

[7] 王洪洋, 廖桂生, 吴云韬. 欠采样频率估计方法[J]. 电子学报, 2004, 32(12): 1978-1981.

[8] Li X W, Liang H, and Xi X G. A robust Chinese remainder theorem with its applications in frequency estimation from under-sampled waveforms[J]., 2009, 40(11): 4314-4322.

[9] Maroosi A and Bizaki H K. Digital frequency determination of real waveforms based on multiple sensors with low sampling rates[J]., 2012, 12(5): 1483-1495.

[10] 郭东亮, 张铁军, 戴宪华. 基于非均匀采样的信号频率, 幅值和相位检测[J]. 系统工程与电子技术, 2012, 34(4): 662-665.

[11] Bourdoux A, Pollin S, Dejonghe A,.. Sparse signal sensing with non-uniform undersampling and frequency excision[C]. International ICST Conference on CROWNCOM, Osaka, 2011: 246-250.

[12] 李安, 王殊, 屈晓旭, 等.基于非均匀采样的空时级联频率和到达角估计[J].系统工程与电子技术, 2010, 32(3): 478-482.

[13] 邵华, 苏卫民, 顾红. 一种非等间距线阵的DOA估计方法[J].电子与信息学报, 2011, 33(1): 95-99.

[14] Weber R J and Huang Y. A joint frequency and DOA estimation algorithm with diagonal load[C]. IEEE Aerospace Conference, Big Sky, MT, 2012: 1-6.

[15] Chen H and Wang Y L. A modified method of frequency and 2-D angle estimation[C]. IEEE Antennas and Propagation Society International Symposium, Columbus, OH , USA, 2003: 920-923.

[16] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2009: 466-479.

赵 曼： 男，1989年生，硕士生，研究方向为阵列信号处理.

陈 辉： 男，1974年生，教授，博士生导师，研究方向为雷达信号处理、阵列信号处理、空时自适应等.

Multichannel Joint Frequency and DOA Estimation Based on Expanded Dimension

Zhao Man Chen Hui

(430019,)

A method of multichannel joint frequency and Direction Of Arrival (DOA) estimation is proposed for the signal with wide frequency band. Under the condition of sub-Nyquist spatio-temporal sampling, the method can provide unambiguous frequency and DOA estimation. According to the space-time two-dimension unambiguous array presented in the paper, the expanded dimension of multiple sampling channels solves the issue of temporal undersampling, and the expanded dimension of multiple snapshot channels overcomes the issue of spatial undersampling. Using the temporal filtering, the estimated frequency and DOA are cascaded, and the pairing of the estimated frequency and DOA is automatically determined. In addition, the spatio-temporal cascaded method can avoid the 2-D spectral peak searching and high-dimensional eigenvalue decomposition, which reduces the computational complexity. Simulation results demonstrate the effectiveness of the novel method.

Array signal processing; Sub-Nyquist spatio-temporal sampling; Space-time two-dimension unambiguous array; Multichannel joint; Frequency estimation; Direction Of Arrival (DOA) estimation

TN911.7

A

1009-5896(2014)01-0147-05

10.3724/SP.J.1146.2013.00472

2013-04-11收到，2013-08-12改回

新世纪优秀人才支持计划(NCET-10-0903)和电子信息控制重点实验室资助课题

陈辉 chhglr@sina.com